10.1函数的图像同步练习（含解析）

中小学教育资源及组卷应用平台
10.1函数的图像
学校:___________姓名：___________班级：___________考号：___________
一、单选题
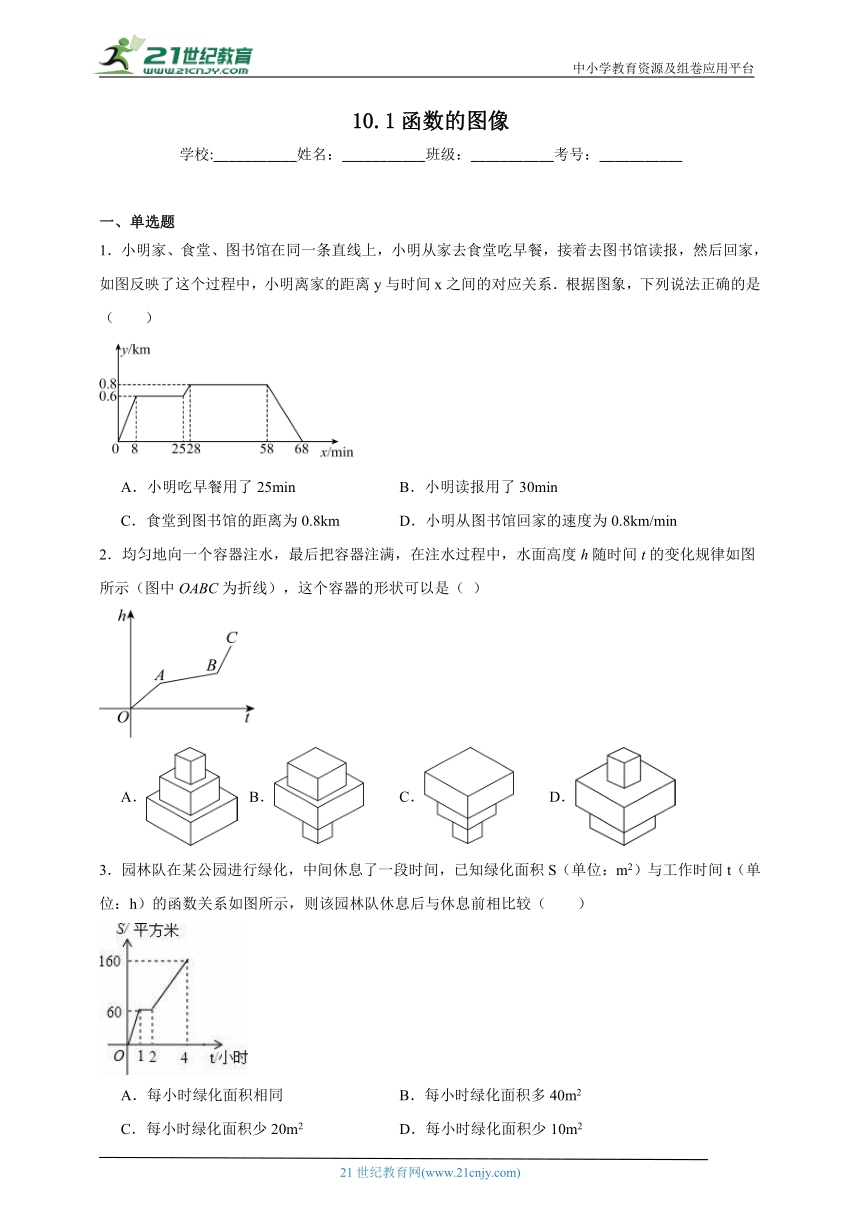
1．小明家、食堂、图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y与时间x之间的对应关系．根据图象，下列说法正确的是（　　）
A．小明吃早餐用了25min B．小明读报用了30min
C．食堂到图书馆的距离为0.8km D．小明从图书馆回家的速度为0.8km/min
2．均匀地向一个容器注水，最后把容器注满，在注水过程中，水面高度h随时间t的变化规律如图所示（图中OABC为折线），这个容器的形状可以是（ ）
A． B． C． D．
3．园林队在某公园进行绿化，中间休息了一段时间，已知绿化面积S（单位：m2）与工作时间t（单位：h）的函数关系如图所示，则该园林队休息后与休息前相比较（　　）
A．每小时绿化面积相同 B．每小时绿化面积多40m2
C．每小时绿化面积少20m2 D．每小时绿化面积少10m2
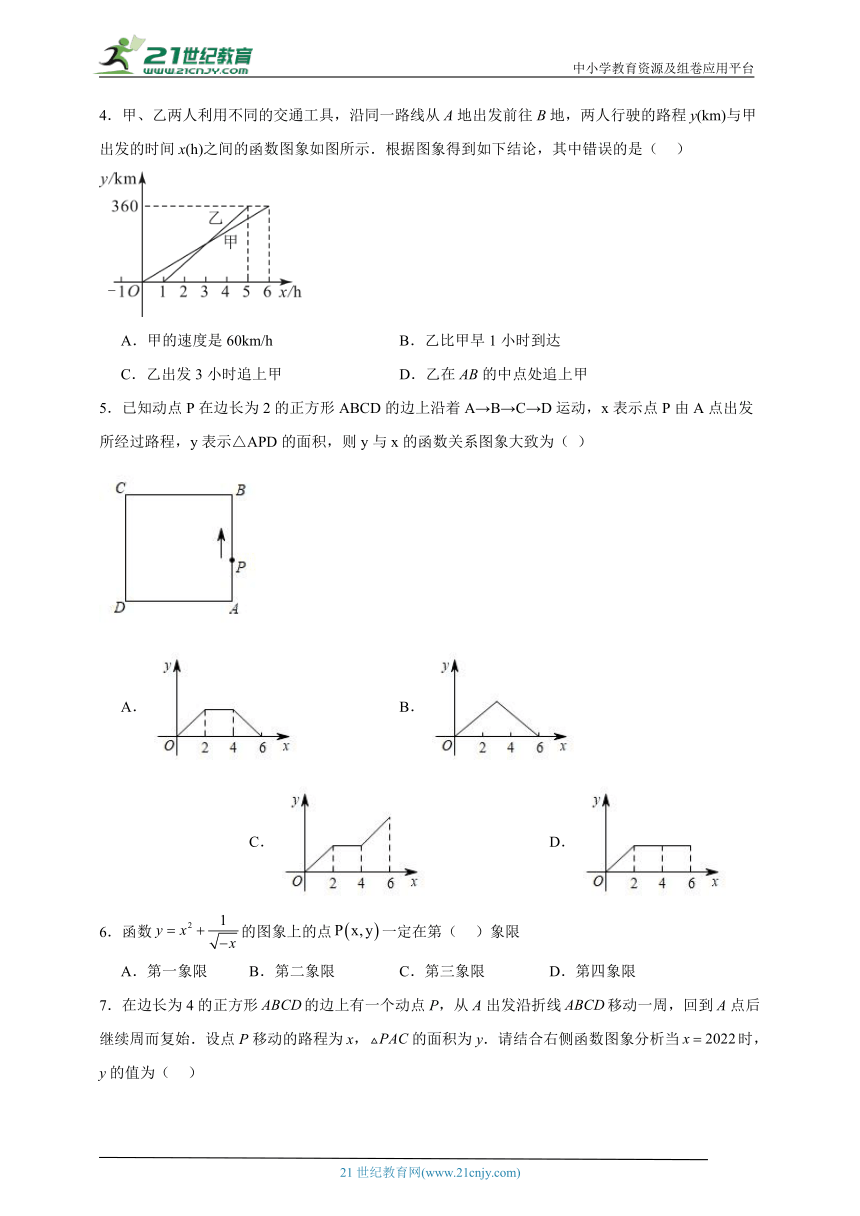
4．甲、乙两人利用不同的交通工具，沿同一路线从A地出发前往B地，两人行驶的路程y(km)与甲出发的时间x(h)之间的函数图象如图所示．根据图象得到如下结论，其中错误的是（ ）

A．甲的速度是60km/h B．乙比甲早1小时到达
C．乙出发3小时追上甲 D．乙在AB的中点处追上甲
5．已知动点P在边长为2的正方形ABCD的边上沿着A→B→C→D运动，x表示点P由A点出发所经过路程，y表示△APD的面积，则y与x的函数关系图象大致为（ ）
A． B． C． D．
6．函数的图象上的点一定在第（ ）象限
A．第一象限 B．第二象限 C．第三象限 D．第四象限
7．在边长为4的正方形的边上有一个动点P，从A出发沿折线移动一周，回到A点后继续周而复始．设点P移动的路程为x，的面积为y．请结合右侧函数图象分析当时，y的值为（ ）
A．2 B．4 C．6 D．8
8．龟兔赛跑之后，输了比赛的兔子决定和乌龟再赛一场．图中的函数图象表示了龟兔再次赛跑的过程（x表示兔子和乌龟从起点出发所走的时间，分别表示兔子与乌龟所走的路程）．下列说法错误的是( )
A．兔子和乌龟比赛路程是500米 B．中途，兔子比乌龟多休息了35分钟
C．兔子比乌龟多走了50米 D．比赛结果，兔子比乌龟早5分钟到达终点
9．函数的自变量的取值范围是（ ）
A． B．且 C． D．且
10．某种铅笔每支售价0.5元，在坐标平面内表示1支到50支铅笔售价的图象是（ ）（提醒：铅笔的支数必须是整数哦）
A．一条直线段 B．一条直线 C．一组有限的不同点 D．以上答案都不是
11．如图，设甲、乙两车在同一直线公路上匀速行驶，开始甲车在乙车的前面，当乙车追上甲车后，两车停下来，把乙车的货物转给甲车，然后甲车继续前行，乙车原地返回．设x小时后两车间的距离为y千米，y关于x的函数关系如图所示，则乙车的速度为（　　）
A．60千米/小时 B．70千米/小时
C．75千米/小时 D．80千米/小时
12．以下四点中，在函数图象上的点是（ ）
A． B． C． D．
二、填空题
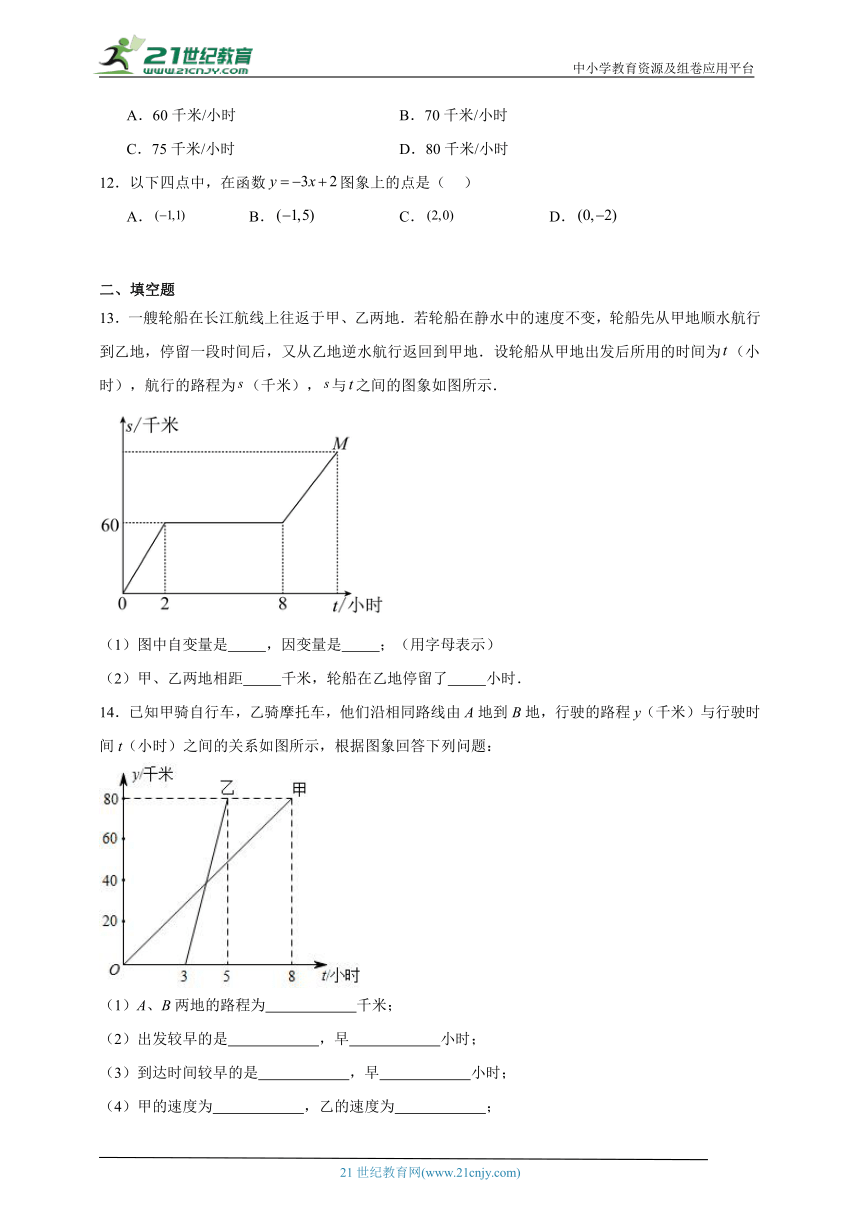
13．一艘轮船在长江航线上往返于甲、乙两地．若轮船在静水中的速度不变，轮船先从甲地顺水航行到乙地，停留一段时间后，又从乙地逆水航行返回到甲地．设轮船从甲地出发后所用的时间为（小时），航行的路程为（千米），与之间的图象如图所示．
（1）图中自变量是 ，因变量是 ；（用字母表示）
（2）甲、乙两地相距 千米，轮船在乙地停留了 小时．
14．已知甲骑自行车，乙骑摩托车，他们沿相同路线由A地到B地，行驶的路程y（千米）与行驶时间t（小时）之间的关系如图所示，根据图象回答下列问题：
（1）A、B两地的路程为 千米；
（2）出发较早的是 ，早 小时；
（3）到达时间较早的是 ，早 小时；
（4）甲的速度为 ，乙的速度为 ；
（5）乙在距A地 千米处追及甲，此时甲行驶了 小时，乙行驶了 小时．
15．已知动点P从点A出发沿图1的边框（边框拐角处都互相垂直）按的路径移动，相应的的面积关于移动路程的关系图象如图2，若，根据图象信息回答，下列说法正确的有： （填写正确的序号）

①图1中长为；
②图2中m的值为9，n的值为25；
③当P点运动到F点时，y对应的值为4；
④当的面积为2时，对应的x的值是2或24．
16．如图1，在长方形中，动点从点出发，沿方向运动至点B处停止，在这个变化过程中，变量表示点运动的路程，变量表示的面积，图2表示变量随的变化情况，则当时，点所在的边是 ．
17．如图，长方形中，，，点从点出发，沿长方形的边做逆时针运动，设点运动的距离为，的面积为，如果，那么关于的函数关系式是 .
三、解答题
18．下面是小林画出函数的一部分图象，利用图象回答：
（1）自变量x的取值范围．
（2）当x取什么值时，y的最小值．最大值各是多少？
（3）在图中，当x增大时，y的值是怎样变化？

19．如图①，在矩形中，AB=30cm，BC=60cm．点从点出发，沿路线向点匀速运动，到达点后停止；点从点出发，沿路线向点匀速运动，到达点后停止．若点同时出发，在运动过程中，点停留了，图②是两点在折线上相距的路程S(cm)与时间(s)之间的部分函数关系图象．求：
（1）P、Q两点的运动速度及P到C点的时间；
（2）设的面积为，求与之间的关系式．
20．用描点法画出函数y＝x＋2的图象．
21．甲、乙两车沿一条路从城出发匀速行驶至城，在整个行驶过程中，甲、乙离开城的距离与甲车行驶的时间之间的函数关系如图所示，根据图象信息解答下列问题：
(1)甲车的速度是______；
(2)乙车用了______小时到达城；
(3)乙车追上甲车时，他们离开城多少千米？
22．如图1，长方形中，，点从B出发，沿方向运动，经过D，C，到B停止，点的速度为每秒，秒时点改变速度，变为每秒，图2是点出发t秒后的面积与t（秒）的关系图象．
(1)直接写出 ， ， ；
(2)设点离开点B的路程为，求出路程与运动时间t（秒）的关系式；
(3)直接写出，当点出发多少秒后，．
23．已知两个变量x，y之间的变化情况如图所示，根据图象回答下列问题：
(1)写出y的变化范围；
(2)求当x＝0，－3时，y的对应值；
(3)求当y＝0，3时，对应的x的值；
(4)当x为何值时，y的值最大？
(5)当x在什么范围内时，y的值在不断增加？
24．小红星期天从家里出发骑车去舅舅家做客，当她骑了一段路时，想起要买个礼物送给表弟，于是又折回到刚经过的一家商店，买好礼物后又继续骑车去舅舅家，如图是她本次去舅舅家所用的时间与小红离家的距离的关系式示意图．根据图中提供的信息回答下列问题：
(1)小红家到舅舅家的路程是 　　米，小红在商店停留了 　　分钟；
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快？最快的速度是多少米/分？
(3)本次去舅舅家的行程中，小红一共行驶了多少米？
《10.1函数的图像》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B D D C A B B C D C
题号 11 12
答案 B B
1．B
【详解】分析：根据函数图象判断即可．
详解：小明吃早餐用了（25-8）=17min，A错误；
小明读报用了（58-28）=30min，B正确；
食堂到图书馆的距离为（0.8-0.6）=0.2km，C错误；
小明从图书馆回家的速度为0.8÷10=0.08km/min，D错误；
故选B．
点睛：本题考查的是函数图象的读图能力．要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合题意正确计算是解题的关键．
2．D
【详解】解：注水量一定，函数图象的走势是稍陡，平，陡；那么速度就相应的变化，跟所给容器的粗细有关．则相应的排列顺序就为D．
故选D．
【点睛】本题考查了函数的实际应用，解决此题的关键是理解相关过程．
3．D
【分析】根据图象可得，休息后园林队2小时绿化面积为160-60=100平方米，然后可得绿化速度．
【详解】解：根据图象可得，休息后园林队2小时绿化面积为160-60=100平方米，
每小时绿化面积为100÷2=50（平方米），
休息前每小时绿化面积60（平方米），
60-50=10（平方米）．
故选D．
【点睛】此题主要考查了函数图象，关键是正确理解题意，从图象中找出正确信息．
4．C
【分析】由速度=路程时间，可求出甲的速度，从而得出结论A正确；由速度=路程:时间，可求出乙的速度，再用甲出发l小时的路程甲、乙速度差，可求出乙出发2小时追上甲，从而结论C错误；由，可得出乙比甲早1小时到达，于是结论B正确；由乙行完全程要4小时，2小时追上甲，即可得出乙在AB的中点处追上甲，结论D正确.即可得出结论．
【详解】解：A、∵甲的速度为（km/h），
∴结论A正确，不符合题意；
B、∵（h），
∴乙比甲早1小时到达，结论B正确，不符合题意；
C、∵乙的速度为（km/h），
（h），
∴乙出发2小时追上甲，结论C错误，符合题意；
D、∵，
∴乙在AB的中点处追上甲，结论D正确，不符合题意．
故选：C．
【点睛】本题考查了从函数图象中获取信息，观察函数图象逐一分析四个结论的正误是解题的关键．
5．A
【详解】P点在AB上运动，△APD的面积，可认为高AD不变，底边AP增大，即面积不断增大．
当P点在CB上运动，△APD的面积，可认为高AB不变，底边AD不变，即面积不变，
P点在CD上运动，△APD的面积，可认为底AD不变，高DP减小，即面积不断减小．
结合图象可知A正确．
故选A．
6．B
【分析】由二次根式和分式有意义的条件，得到，然后判断得到，即可得到答案．
【详解】解：根据题意，则
∵，解得：，
∴，，
∴，
∴点一定在第二象限；
故选：B．
【点睛】本题考查了二次根式和分式有意义的条件，以及判断点所在的象限，解题的关键是熟练掌握所学的知识进行解题．
7．B
【分析】要对点P所在的位置进行分类：①当点P在线段上移动；②当点P在线段上移动；③当点P在线段上移动；④当点P在线段上移动；探讨得出规律即可．
【详解】①当点P在线段上移动，
即时，；
②当点P在线段上移动，
即时，；
③当点P在线段上移动，
即时，；
④当点P在线段上移动，
即时，，
点P的运动轨迹以16为单位循环，
当时，，
此时，
故答案为：B．
【点睛】本题考查动点函数问题，分段函数的应用，函数的解析式的求法以及动点的运动规律，分类探讨是解决问题的关键．
8．C
【分析】依据函数图象进行分析即可求解．
【详解】由函数图象可知：兔子和乌龟比赛的路程为500米，
兔子休息的时间为50-10=40分钟，乌龟休息的时间为35-30=5分钟，即兔子比乌龟多休息40-5=35分钟，
比赛中兔子用时55分钟，乌龟用时60分钟，兔子比乌龟早到终点5分钟，
据此可知C项表述错误，
故选：C．
【点睛】本题考查了根据函数图象获取信息的知识，读懂函数图象的信息是解答本题的关键．
9．D
【分析】由分式与二次根式有意义的条件得函数自变量的取值范围．
【详解】解：由题意得：
解得：且
故选D．
【点睛】本题考查的是函数自变量的取值范围，掌握分式与二次根式有意义的条件是解题的关键．
10．C
【详解】∵函数的解析式为：y=0.5x（x为正整数，且1≤x≤50），
∴在坐标平面内表示为一条直线上的50个点．
故选C．
11．B
【分析】设甲车的速度是a千米/小时，乙车的速度为b千米/小时，根据函数图象反应的数量关系建立方程组求出其解即可．
【详解】解：设甲车的速度是a千米/小时，乙车的速度为b千米/小时，
由题意，得，
解得：
故乙车的速度是70千米/小时，
故选：B．
【点睛】本题考查了二元一次方程组的应用，根据题意，找准等量关系，列出方程是解决本题的关键．
12．B
【分析】本题考查一次函数图象上点的坐标特征的理解和掌握，只要把点的坐标代入函数的解析式，若左边右边，则点在函数的图象上，反之就不在函数的图象上，代入检验即可．
【详解】A选项：把点代入函数中，左边，右边，左边右边，点不在函数的图象上；
B选项：把点代入函数中，左边，右边，左边右边，点在函数的图象上；
C选项：把点代入函数中，左边，右边，左边右边，点不在函数的图象上；
D选项：把点代入函数中，左边，右边，左边右边，点不在函数的图象上．
故选：B
13． 60 6
【分析】本题考查用图象表示变量间的关系，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．
（1）根据自变量和因变量的定义进行判断即可；
（2）从图象直接观察即可得出答案．
【详解】解：（1）由图象可知：自变量是t，因变量是s；
故答案为：t；s；
（2）由图象可知：甲乙两地相距60千米，
轮船在乙地停留了（小时）；
故答案为：60；6．
14． 80 甲 3 乙 3 10千米/小时 40千米小时 40 4 1
【分析】（1）从函数的图象可以看出路程为80千米；
（2）自行车早出发3小时;
（3）到达较早的是摩托车；
（4）用路程除以时间即可得到速度；
（5）当两个图象有交点的时，两车相遇．
【详解】解：（1）从图象上可以看出两地的路程为80千米；
（2）出发较早的是自行车，早3小时；
（3）到达时间较早的是摩托车，早3小时；
（4）甲的速度为：80÷8=10千米/小时；
乙的速度是80÷2=40千米/小时；
（5）设甲行驶了t小时乙追上甲，
根据题意，10t=40(t-3)，
解得：t=4，
40(t-3)=40(千米)，
∴乙距A地40千米的处追及甲，此时甲行驶了4小时，乙行驶了1小时；
故答案为：（1）80；（2）甲，3；（3）乙，3；（4）10千米/小时，40千米/小时；（5）40，4，1．
【点睛】本题考查了函数的图象，正确的识别图象是解题的关键．
15．①③
【分析】本题主要考查了从函数图象获取信息，根据函数图象可知当时，点P在上运动，当，点P在上运动，据此可判断①；则，，根据当点P运动到直线与交点处时，y的值为0，得到，据此可判断②；则当P点运动到F点时，y对应的值为，据此可判断③；分当时，当时， 当时，三种情况求出x的值即可判断④．
【详解】解：由函数图象可知，当时，y随x增大而增大，当时，y保持不变，
∴当时，点P在上运动，当，点P在上运动，
∴，故①正确；
同理可得上，点P在上运动，则，
∴；
当点P运动到直线与交点处时，y的值为0，
∴，故②错误；
∴当P点运动到F点时，y对应的值为，故③正确；
当时，，解得，
当时，，解得；
当时，，解得，
∴当的面积为2时，对应的x的值是2或24或28，故④错误；
故答案为：①③．
16．或
【分析】先根据函数图象得出，，然后根据图1，得出面积的最大值为，根据当时，，点R在或边上．
【详解】解：∵时，即点R从C到达点D时，的面积开始不变，
∴，
同理可得：，
∵四边形为长方形，
∴，，
当点R在上运动时，的面积不变，且面积最大，面积为：
，
当时，，
∴点R在或边上．
故答案为：或．
【点睛】本题主要考查了从函数图象中获取信息，三角形面积的计算，解题的关键是根据图2得出，．
17．
【分析】找出当5＜x＜8时，点P的位置，根据AB、AD的长度可找出PC的长度，再根据三角形的面积公式即可找出y关于x的函数关系式．
【详解】当5＜x＜8时，点P在线段BC上，PC=8-x，
∴y=PC AB=-x+20．
故答案为：y=-x+20．
【点睛】本题考查了函数关系式，找出当5＜x＜8时点P的位置是解题的关键．
18．（1）自变量x的取值范围为0≤x≤10；（2）当x＝10时，最小值为5，当x＝0时，最大值为10；（3）当x增大时，y的值反而减小．
【详解】试题分析：（1）观察图象即可得出自变量的取值范围；
（2）观察图象结合解析式即可得；
（3）根据自变量的变化结合图象即可得.
试题解析：（1）由图象可知自变量x的取值范围为0≤x≤10；
（2）看图象上各点对应的函数值，可以知道当x＝10时，最小值为5，
结合解析式可知，当x＝0时，最大值为10；
（3）当x＝10时，最小值为5，当x＝0时，最大值为10，所以可以知道当x增大时，y的值反而减小.
【点睛】本题考查了函数的图象、自变量的取值范围等，结合图象以及解析式的特点进行解题是关键.
19．(1) P点运动的速度为30Q点运动的速度为15；P到C点的时间为3s；(2)
【分析】(1)利用函数图象得出当P、Q两点在函数关系图象上的F点到G点两点路程随时间变化减慢得出此时Q点停留，只有P点运动，再利用纵坐标的值得出P点和Q点运动速度；可求得P到C点的时间；
(2)根据P、Q的位置不同，进行分类讨论得出答案即可．
【详解】(1)由函数图象得出，当P、Q两点在F点到G点两点路程随时间变化减慢得出此时Q点停留1秒，只有P点运动，此时S的值由75下降到45，时间t=1s，
∴P点运动的速度为：30
再根据函数图象E点到F点，S的值由120变为75，时间为t=1s，
∴，
∴Q点速度为：，
P到C点的时间：；
(2)当时，
，
∴；
当时，P、B重合，
∴；
当时，P点运动、Q点不动，
，，
∴；
当时，
，，
∴；
当时，P、C、Q重合，
∴；
当时，
，，
∴；
当时，P到达终点D，
，
∴；
当时，B、Q重合，
∴；
当时，
，
∴；
综上，．
【点睛】本题主要考查了动点问题的函数图象以及求动点函数的解析式，利用分类讨论思想解决问题是本题的关键．
20．见解析
【详解】解：列表、描点、连线后得到的图象，如图所示.
21．(1)
(2)3
(3)
【分析】本题考查函数的图象，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
（1）根据函数图象可知甲车5小时行驶了300公里；
（2）根据函数图象可知甲车出发1小时后乙车出发，用了3小时到达；
（3）根据题意求出乙车的速度，再列方程解答即可；
【详解】（1）解：由题意得，甲车的速度是：．
故答案为：；
（2）由题意可知，乙车用了3小时到达城；
故答案为：3；
（3）乙车的速度为：，
设乙车出发后小时追上甲车，根据题意得：
，
解得，
乙车出发后1.5小时追上甲车；此时他们离开城的距离是
答：乙车追上甲车时，他们离开城150千米.
22．(1)5；；4
(2)
(3)或
【分析】本题考查动点问题的函数图象，一元一次方程的实际应用，从函数图象获取信息是解题的关键．
（1）根据a秒时的面积可求a的值，由6.5秒时，点P与点D重合，利用路程速度时间，即可求出k的值，由时间路程速度即可求出b的值；
（2）分为点P速度为每秒和点P速度为每秒，两种情况由路程速度时间，列出关系式即可；
（3）分为点P在上和点P在上，两种情况讨论即可．
【详解】（1）解：根据图象可得：a秒时的面积为12，即，
，
，
；
6.5秒时，点P与点D重合，
；
点P从点D运动到点B的速度为每秒，
，
长方形中，，
；
（2）解：点P速度为每秒时：；
点P速度为每秒时：；
综上，；
（3）解：点P在上时，
当点P加速前：
，
（舍去，不符合题意），
当点P加速后：
，
；
当点P运动到点C时，所需时间为：（秒），
点P在上时，，
，
，
综上，当点出发或时，．
23．(1)y的变化范围为－2～4;(2)当x＝0时，y＝3；当x＝－3时，y＝1.(3)当y＝0时，x1＝－2.5，x2＝－1.5，x3＝3.5；当y＝3时，x1＝0，x2＝2.(4)当x＝1时，图象有最高点，此时y最大.(5)当x在－2～1时，y的值在不断增加.
【分析】（1）根据函数图象的最高点和最低点的纵坐标，可得答案；
（2）根据自变量的值与函数值的对应关系，即可得出相应的函数值；
（3）根据函数值，即可得出相应自变量的值；
（4）根据函数图象的最高点对应的自变量的值即可得出答案；
（5）根据函数图象上升部分的横坐标，即可得出自变量的范围．
【详解】(1)根据函数图象可得：y的变化范围为－2～4.
(2)当x＝0时，y＝3；当x＝－3时，y＝1.
(3)当y＝0时，x1＝－2.5，x2＝－1.5，x3＝3.5；
当y＝3时，x1＝0，x2＝2.
(4)当x＝1时，图象有最高点，此时y最大.
(5)当x在－2～1时，函数图象上升，y的值在不断增加.
【点睛】本题考查了函数图象，观察函数图象的变化趋势获得有效信息是解题关键．
24．(1)1500，4
(2)小红在12﹣14分钟最快，450米/分
(3)2700米
【分析】（1）根据图象，路程的最大值即为小红家到舅舅家的路程；读图，对应题意找到其在商店停留的时间段，进而可得其在书店停留的时间；
（2）分析图象，找函数变化最快的一段，可得小明骑车速度最快的时间段，进而可得其速度；
（3）分开始行驶的路程，折回商店行驶的路程以及从商店到舅舅家行驶的路程三段相加即可求得小红一共行驶路程．
【详解】（1）解：据图象舅舅家纵坐标为1500，小红家的纵坐标为0，
故小红家到舅舅家的路程是1500米；据题意，小红在商店停留的时间为从8分到12分，故小红在商店停留了4分钟．
故答案为：1500，4；
（2）解：根据图象，时，直线最陡，
故小红在12﹣14分钟最快，速度为（米/分）；
（3）解：本次去舅舅家的行程中，小红一共行驶了：（米）．
【点睛】本题考查利用函数的图象解决实际问题，正确理解函数图象横纵坐标表示的意义，理解问题的过程，就能够通过图象得到函数问题的相应解决．需注意计算单位的统一
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)