第六章平行四边形同步练习（含解析）

中小学教育资源及组卷应用平台
第六章平行四边形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
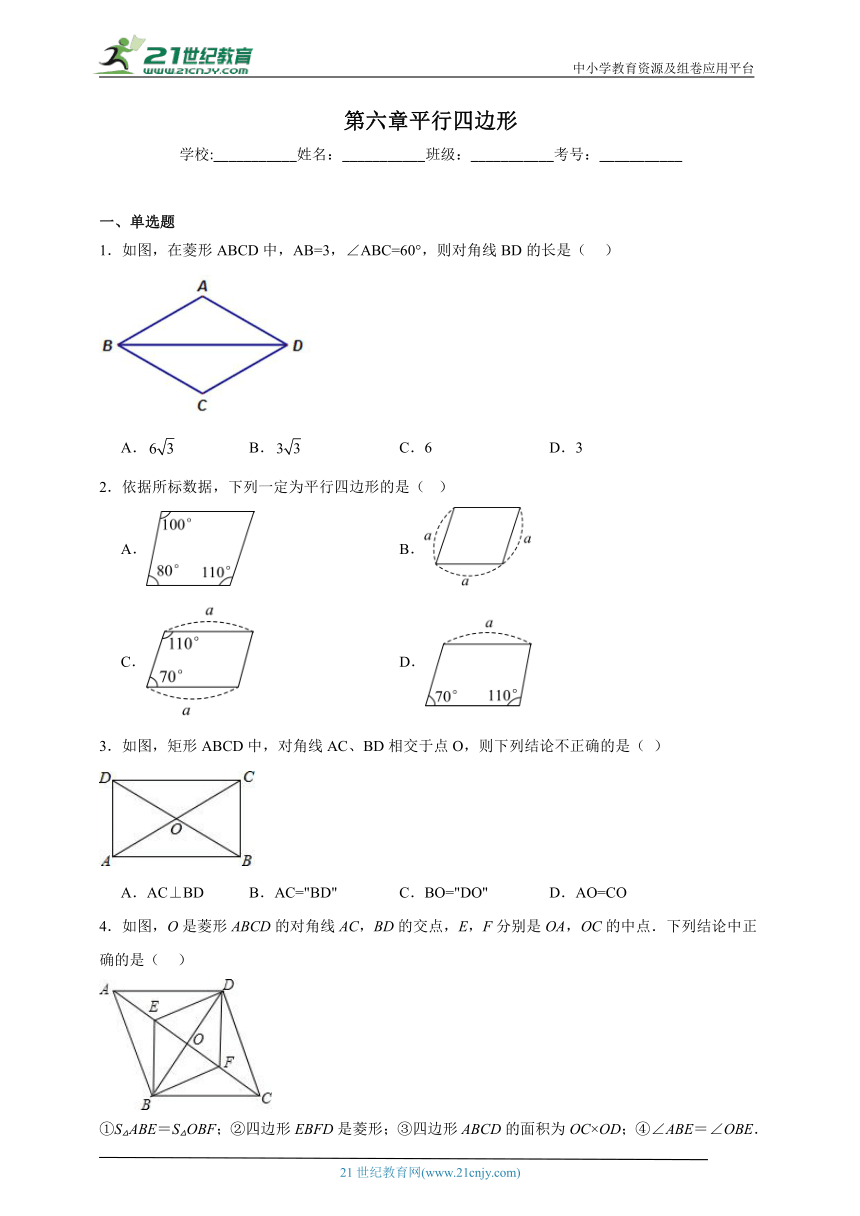
1．如图，在菱形ABCD中，AB=3，∠ABC=60°，则对角线BD的长是（ ）
A． B． C．6 D．3
2．依据所标数据，下列一定为平行四边形的是（ ）
A． B．
C． D．
3．如图，矩形ABCD中，对角线AC、BD相交于点O，则下列结论不正确的是（ ）
A．AC⊥BD B．AC="BD" C．BO="DO" D．AO=CO
4．如图，O是菱形ABCD的对角线AC，BD的交点，E，F分别是OA，OC的中点．下列结论中正确的是（ ）
①S△ABE＝S△OBF；②四边形EBFD是菱形；③四边形ABCD的面积为OC×OD；④∠ABE＝∠OBE．
A．①② B．②④ C．②③ D．③④
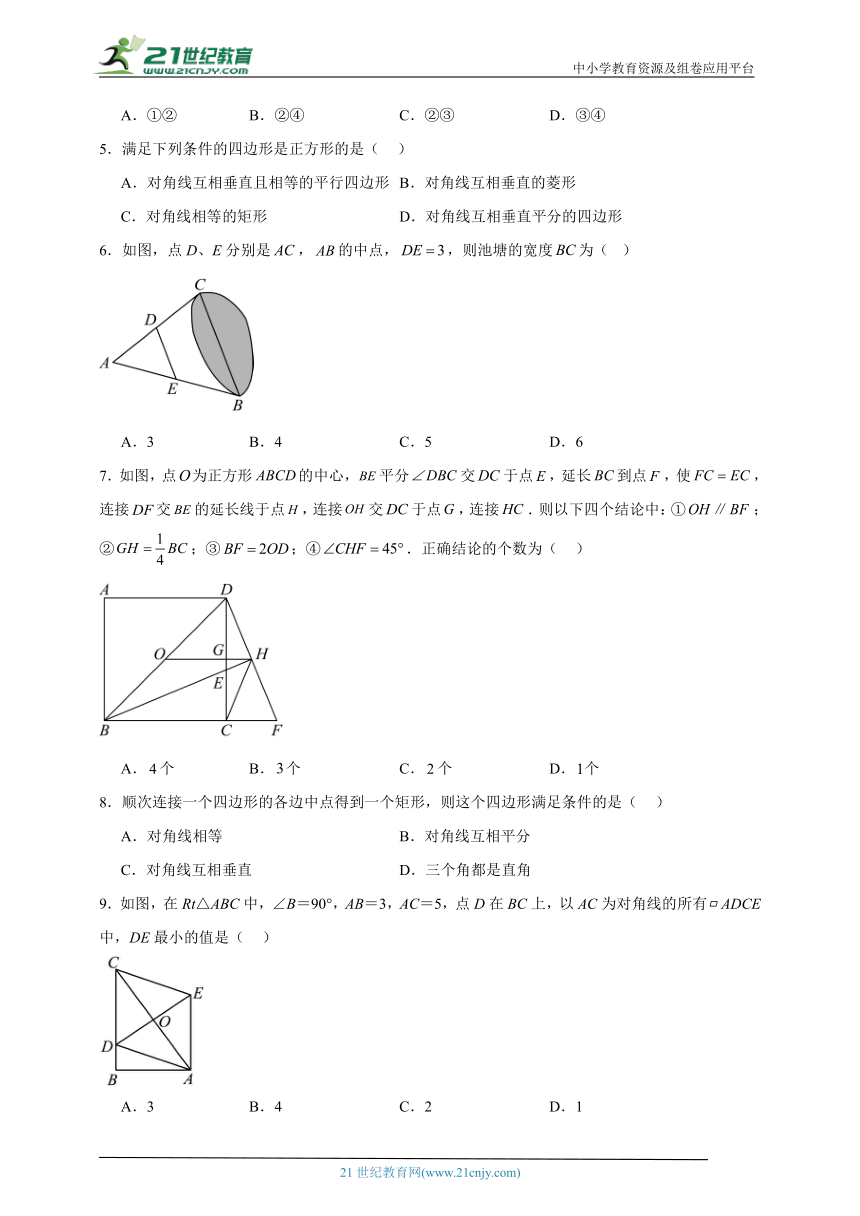
5．满足下列条件的四边形是正方形的是（ ）
A．对角线互相垂直且相等的平行四边形 B．对角线互相垂直的菱形
C．对角线相等的矩形 D．对角线互相垂直平分的四边形
6．如图，点D、E分别是，的中点，，则池塘的宽度为（ ）
A．3 B．4 C．5 D．6
7．如图，点为正方形的中心，平分交于点，延长到点，使，连接交的延长线于点，连接交于点，连接．则以下四个结论中：①；②；③；④．正确结论的个数为（ ）

A．个 B．个 C．个 D．个
8．顺次连接一个四边形的各边中点得到一个矩形，则这个四边形满足条件的是（ ）
A．对角线相等 B．对角线互相平分
C．对角线互相垂直 D．三个角都是直角
9．如图，在Rt△ABC中，∠B＝90°，AB＝3，AC＝5，点D在BC上，以AC为对角线的所有ADCE中，DE最小的值是（ ）
A．3 B．4 C．2 D．1
10．若矩形对角线相交所成钝角为120°，短边长3.6，则对角线的长为( )．
A．3.6 B．7.2 C．1.8 D．14.4
11．如图所示，平面直角坐标系中，已知三点A（－1，0），B（2，0），C（0，1），若以A、B、C、D为顶点的四边形是平行四边形，则D点的坐标不可能是（ ）
A．（3，1） B．（－3，1） C．（1，3） D．（1，－1）
12．添加下列一个条件，能使平行四边形成为菱形的是（ ）

A． B． C． D．
二、填空题
13．如图，在四边形ABCD中，AB∥DC，E是AD中点，EF⊥BC于点F，BC=5，EF=3．
（1）若AB=DC，则四边形ABCD的面积S= ；
（2）若AB＞DC，则此时四边形ABCD的面积S′ S（用“＞”或“=”或“＜”填空）．

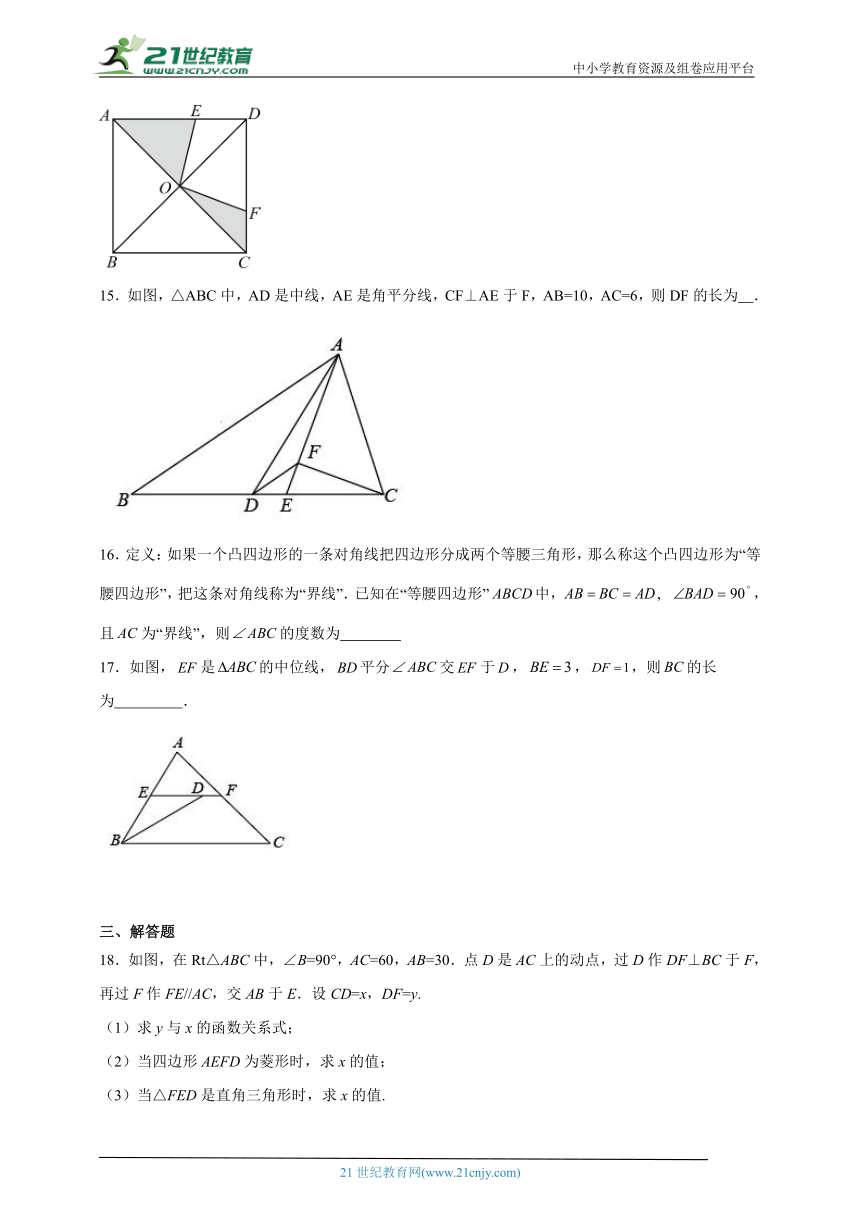
14．如图，点E、F分别是正方形的边、上的点，且，已知，则图中阴影部分的面积是 ．
15．如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=10，AC=6，则DF的长为 ．
16．定义：如果一个凸四边形的一条对角线把四边形分成两个等腰三角形，那么称这个凸四边形为“等腰四边形”，把这条对角线称为“界线”．已知在“等腰四边形”中，，且为“界线”，则的度数为
17．如图，是的中位线，平分交于，，，则的长为 ．
三、解答题
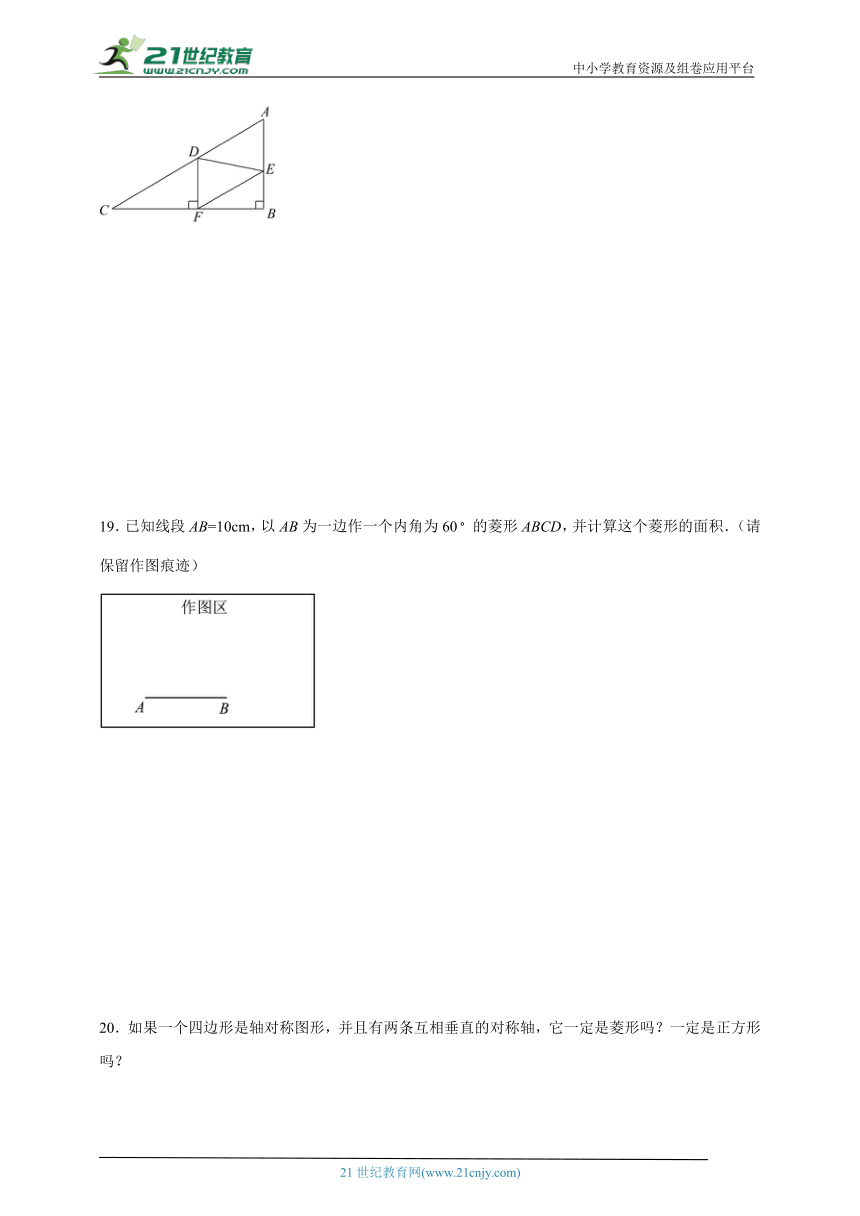
18．如图，在Rt△ABC中，∠B=90°，AC=60，AB=30．点D是AC上的动点，过D作DF⊥BC于F，再过F作FE//AC，交AB于E．设CD=x，DF=y.
（1）求y与x的函数关系式；
（2）当四边形AEFD为菱形时，求x的值；
（3）当△FED是直角三角形时，求x的值.
19．已知线段AB=10cm，以AB为一边作一个内角为60 的菱形ABCD，并计算这个菱形的面积．（请保留作图痕迹）
20．如果一个四边形是轴对称图形，并且有两条互相垂直的对称轴，它一定是菱形吗？一定是正方形吗？
21．如图，点P、Q、E、F分别为正方形四条边上的点，已知，请判断四边形的形状并证明．
22．如图，已知五边形是正五边形，连接，交于点P． 求证：四边形是平行四边形．
23．在ABCD，过点D作DE⊥AB于点E，点F在边CD上，DF＝BE，连接AF，BF.
（1）求证：四边形BFDE是矩形；
（2）若CF＝3，BF＝4，DF＝5，求证：AF平分∠DAB.
24．如图，在四边形纸片ABCD中，AD∥BC，AD>CD，将纸片沿过点D的直线折叠，使点C落在AD上的点C′处，折痕DE交BC于点E，连结C′E．
（1）求证：四边形CDC′E是菱形；
（2）若BC=CD+AD，试判断四边形ABED的形状，并加以证明．
《第六章平行四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A A D B C A B
题号 11 12
答案 C C
1．B
【分析】连接AC，交BD于点O，先判断出△ABC是等边三角形，再根据菱形的对角线互相垂直平分和等边三角形的性质求出AO、BO，然后根据菱形的对角线互相平分求出BD即可得解．
【详解】解：连接AC，交BD于点O，
∵菱形ABCD中∠ABC=60°，AB=3，
∴△ABC是等边三角形，AB=BC=AC
∴AO=×3=，
∴BO=，
∴BD=2BO=2×=，
故选B
【点睛】本题考查了菱形的性质，等边三角形的判定与性质，熟记菱形的对角线互相垂直平分是解题的关键．
2．C
【分析】根据平行四边形的判定定理解答即可．
本题考查了平行四边形的判定，熟练掌握判定定理是解题的关键．
【详解】解：两组对角都不相等，不能判定是平行四边形，
故A选项错误；
一组对边相等，另一组对边无法判定是否相等，故不能判定是平行四边形，
故B选项错误；
根据，判定长为a的对边相等且平行，能判定是平行四边形，
故C符合题意；
根据，判定一组对边平行，，但是无法判定是否相等，不能判定是平行四边形，
故D不符合题意；
故选：C．
3．A
【详解】试题解析：∵四边形ABCD是矩形，
∴AC=BD，BO=DO，AO=CO，
∴A不正确，B、C、D正确；
故选A．
考点：矩形的性质．
4．A
【分析】由菱形的判定与性质分别对各个选项进行判断即可．
【详解】解：四边形是菱形，
，，，
、分别是、的中点，
，
，故①正确；
，，
四边形是平行四边形，
又
四边形是菱形，故②正确；
菱形的面积，故③错误；
四边形是菱形，
，，故④错误；
故选：A．
【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质以及三角形面积等知识；解题的关键是熟练掌握菱形的性质，证明四边形为菱形．
5．A
【分析】根据正方形的判定方法即可求解．
【详解】解：选项，对角线互相垂直且相等的平行四边形是正方形，故选项正确，符合题意；
选项，对角线互相垂直的菱形还是菱形，故选项错误，不符合题意；
选项，对角线相等的菱形是正方形，故选项错误，不符合题意；
选项，对角线互相垂直平分的长方形是正方形，故选项错误，不符合题意；
故选：．
【点睛】本题主要考查正方形的判定，掌握“对角线相互垂直的矩形是正方形”，“对角线相等的菱形是正方形”，“对角线互相垂直且相等的平行四边形是正方形”的知识是解题的关键．
6．D
【分析】本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．根据三角形中位线定理解答即可．
【详解】解：∵点D、E分别是边、AC的中点，
∴是的中位线，
∴，
故选：D．
7．B
【分析】本题主要考查正方形的性质、全等三角形的判定及性质、角平分线的定义、三角形的中位线定理，牢记正方形的性质、全等三角形的判定定理及性质、角平分线的定义、三角形的中位线定理是解题的关键．
①先证得，求得，再证得，进而证得，进而证得为的中点，即可判断该说法是否正确．
②根据，，，即可判断该说法是否正确．
③根据，即可判断该说法是否正确．
④由题意可求得，结合三角形的外角的性质，判断该说法是否正确．
【详解】①在和中，
，
∴，
∴，
∵，，
∴，
∴，
∴，
∵平分，
∴，
在和中，
，
∴，
∴，
∵为正方形的中心，
∴，
∴，
说法①正确．
②∵为的中位线，
∴，，
∵，
∴，
∵，
∴，
∴，
∵，
∴，
说法②错误．
③∵，
∴，
∵为正方形的中心，
∴，
∴，
说法③正确．
④∵为正方形的中心，
∴，
∵平分，
∴，
∵，
∴，
∵在中，，
∴，
∴，
∴，
说法④正确．
综上所述，说法正确的为①③④，
故选．
8．C
【分析】作如下图所示，根据矩形的性质和三角形中位线定理即可求解．
【详解】解：作如下图，
由E、F、G、H分别是的中点，
根据三角形中位线定理得：，
∵四边形是矩形，
∴，
∴，即对角线互相垂直，
故选C．
【点睛】本题考查了矩形的性质和三角形的中位线定理，解决本题的关键是构造三角形利用三角形中位线定理进行解答．
9．A
【分析】由平行四边形的对角线互相平分、垂线段最短知，当OD⊥BC时，线段DE取最小值，然后证明四边形ABDE是平行四边形，根据平行四边形的性质得到DE．
【详解】解：∵在Rt△ABC中，∠B＝90°，
∴BC⊥AB，
∵四边形ADCE是平行四边形，
∴OD＝OE，OA＝OC，CD∥AE，
∴当OD取最小值时，线段DE最短，此时OD⊥BC，
∴OD∥AB，
∵BD∥AE，
∴四边形ABDE是平行四边形，
∴DE＝AB＝3，
故选：A．
【点睛】本题考查了平行四边形的性质和判定以及垂线段最短等知识；熟练掌握平行四边形的性质是解题的关键．
10．B
【分析】如图，根据矩形性质得出AC=BD，AO=OC=AC，BO=OD=BD，求出OA=OB，得出△AOB是等边三角形，求出AB=AO=OB，即可得出答案．
【详解】如图，
∵四边形ABCD是矩形，
∴AC=BD，AO=OC=AC，BO=OD=BD，
∴OA=OB，
∵∠AOD=120°，
∴∠AOB=180°-120°=60°，
∴△AOB是等边三角形，
∴AB=AO=OB=3.6cm，
∴BD=AC=2AO=7.2cm，
故选B．
【点睛】本题考查了矩形性质和等边三角形的性质和判定的应用，关键是求出等边三角形AOB和求出BD=AC=2AO．
11．C
【分析】先根据平行四边形的判定方法作出图形，即可作出判断.
【详解】解：由图可得D点的坐标可能是（3，1）、（－3，1）、（1，－1），但不可能是（1，3）
故选C.
考点：平行四边形的判定和性质
点评：平行四边形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中半径常见的知识点，一般难度不大，需熟练掌握.
12．C
【分析】根据菱形的判定逐个进行证明，再进行判断即可．
【详解】解：A、中，本来就有，故本选项错误；
B、中，对角线，可判断平行四边形成为矩形，故本选项错误；
C、中，，可利用有一组邻边相等的平行四边形是菱形，判定 ABCD是菱形，故本选项正确；
D、中，一个内角，可判断平行四边形成为矩形，故本选项错误．
故选：C．
【点睛】本题考查了平行四边形的性质，菱形的判定的应用，注意：菱形的判定定理有：①有一组邻边相等的平行四边形是菱形，②四条边都相等的四边形是菱形，③对角线互相垂直的平行四边形是菱形．
13． 15 =
【详解】解：（1）∵AB=DC，AB∥DC，
∴四边形ABCD是平行四边形，
∴四边形ABCD的面积S=5×3=15，
故答案为：15
（2）如图，连接EC，延长CD、BE交于点P，

∵E是AD中点，
∴AE=DE，
又∵AB∥CD，
∴∠ABE=∠P，∠A=∠PDE，
在△ABE和△DPE中，
∵，
∴△ABE≌△DPE（AAS），
∴S△ABE=S△DPE，BE=PE，
∴S△BCE=S△PCE，
则S四边形ABCD=S△ABE+S△CDE+S△BCE
=S△PDE+S△CDE+S△BCE
=S△PCE+S△BCE
=2S△BCE
=2××BC×EF
=15，
∴当AB＞DC，则此时四边形ABCD的面积S′=S，
故答案为：=
14．9
【分析】根据正方形的性质得到∠EDO＝∠FCO，AC⊥BD，OD＝BD，OC＝AC，AC＝BD，根据全等三角形的判定定理得到△ODE≌△OCF（ASA），根据正方形的面积公式即可得到结论．
【详解】解：∵四边形ABCD是正方形，
∴∠EDO＝∠FCO，AC⊥BD，OD＝BD，OC＝AC，AC＝BD，
∴∠DOC＝90°，OD＝OC，
∵OE⊥OF，
∴∠EOF＝90°，
∴∠DOE＝∠COF，
∴△ODE≌△OCF（ASA），
∴图中阴影部分的面积＝S△AOD＝S正方形ABCD，
∵AD＝6，
∴图中阴影部分的面积＝×62＝9，
故答案为：9．
【点睛】本题考查了正方形的性质，全等三角形的判定和性质，证得△ODE≌△OCF是解题的关键．
15．2
【详解】如图，延长CF交AB于点G，
∵在△AFG和△AFC中，
∠GAF=∠CAF，AF=AF，∠AFG=∠AFC，
∴△AFG≌△AFC（ASA）．
∴AC=AG，GF=CF．
又∵点D是BC中点，
∴DF是△CBG的中位线．
∴DF=BG=（AB﹣AG）=（AB﹣AC）=2．
16．60°或90°或150°
【分析】根据题意，分三种情况：①如图1，当AD=AC时，②如图2，当AD=CD时，③如图3，当AC=CD时，分别求出的度数，即可．
【详解】∵在“等腰四边形”中，，且为“界线”，
①如图1，当AD=AC时，
∴AB=AC=BC，∠ACD=∠ADC，
∴△ABC是正三角形，
∴=∠BAC=∠BCA=60°；
②如图2，当AD=CD时，
∴AB=AD=BC=CD，
∵∠BAD=90°，
∴四边形ABCD是正方形，
∴=90°；
③如图3，当AC=CD时，过点C作CE⊥AD于E，过点B作BF⊥CE于F，
∵AC=CD，CE⊥AD，
∴AE=AD，∠ACE=∠DCE，
∵∠BAD=∠AEF=∠BFE=90°，
∴四边形ABFE是矩形，
∴BF=AE，
∵AB=AD=BC，
∴BF=BC，
∴∠BCF=30°，∠CBF=60°，
∴=60°+90°=150°．
综上所述：的度数为60°或90°或150°．
故答案是：60°或90°或150°．
【点睛】本题主要考查等腰三角形的性质，直角三角形的性质与四边形的综合，掌握等腰三角形“三线合一”以及直角三角形的性质定理，是解题的关键．
17．8
【分析】利用等腰三角形的性质求出DE＝3，可得EF＝4，再利用三角形的中位线定理解决问题即可．
【详解】∵EF是△ABC的中位线，
∴EF∥BC，BC＝2EF，
∴∠EDB＝∠DBC，
∵BD平分∠EBC，
∴∠EBD＝∠DBC，
∴∠EDB＝∠EBD，
∴EB＝ED＝3，
∵DF＝1，
∴EF＝ED＋DF＝3＋1＝4，
∴BC＝8，
故答案为8．
【点睛】本题考查三角形的中位线定理，等腰三角形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
18．（1）；（2）40；（3）30或48.
【分析】（1）利用直角三角形中30°角的性质即可得出y与x的函数关系式；
（2）利用菱形的性质得出AD=DF，从而可得y=60﹣x，然后解方程组即可得出x的值；
（3）由题意可得当△EDF是直角三角形时，只能是∠EDF=90°．由△DEF是直角三角形，列出方程60-x=2y，与y=x组成方程组求x的值．
【详解】解：（1）∵在Rt△ABC中，∠B=90°，AC=60，AB=30，
∴∠C=30°，
∵CD=x，DF=y．
∴；
（2）∵四边形AEFD为菱形，
∴AD=DF，
∴y=60﹣x
∴方程组，
解得x=40，
∴当x=40时，四边形AEFD为菱形；
（3）①当∠FDE=90°时，
∵FE∥AC，
∴∠EFB=∠C=30°，
∵DF⊥BC，
∴∠DEF+∠DFE=∠EFB+∠DFE，
∴∠DEF=∠EFB=30°，
∴EF=2DF，
∴60﹣x=2y，
与，组成方程组，得
解得x=30，
∴当△DEF是直角三角形时，x=30．
②当∠DEF=90°时，
在Rt△ADE中，AD=60-x，∠AED=90°-∠FEB=90°-∠A=30°，
AE=2AD=120-2x，
在Rt△EFB中，EF=AD=60-x，∠EFB=30°，
∴EB=EF=30-x，
∵AE+EB=30，
∴120-2x+30-x=30，
∴x=48．
综上所述，当△DEF是直角三角形时，x的值为30或48．
【点睛】本题主要考查函数解析式，菱形和直角三角形的性质.找出等量关系列方程是解题的关键.
19．
【分析】直接利用菱形的性质以及等边三角形的性质得出D，C点位置，构造等边ABD，即可画出图形，再直接利用菱形面积求法得出答案即可．
【详解】解：解：如图，菱形ABCD即为所求．
连接AC，BD交于点O，
∵四边形ABCD是菱形，
∴AC⊥BD，AD=AB=BC=CD=10cm,
∵∠DAB=∠DCB=60°，
∴ABD，BCD都是等边三角形，
∴BD=AB=AD=10cm,
∴OD=OB=5cm,
∴，
∴BD=10cm,AC=10 cm,
∴S菱形ABCD==．
【点睛】本题考查作图-复杂作图，菱形的判定和性质，等边三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
20．不一定是菱形也不一定是正方形．
【分析】根据菱形和长方形都有两条对称轴，且都互相垂直；正方形有四条对称轴，有两组对称轴互相垂直，即可得出答案．
【详解】如果一个四边形是轴对称图形，并且有两条互相垂直的对称轴，它不一定是菱形，也不一定是正方形，有可能是矩形．如图，
故这个四边形不一定是菱形，也不一定是正方形．
【点睛】本题考查特殊四边形的轴对称，特殊的平行四边形的性质，熟悉特殊四边形的轴对称特点是解答本题的关键．
21．正方形，见解析
【分析】本题主要考查正方形的判定和性质以及全等三角形的判定和性质，根据题意得和，即可证得，则有，进一步证得即可判定为正方形．
【详解】证明：四边形是正方形，证明如下：
∵四边形是正方形，
∴，．
∵，
∴，
∴，
∴，，
∴四边形为菱形．
∵，
∴，
∴，
∴四边形为正方形．
22．见解析
【分析】利用正多边形内角和定理及等边对等角得出，然后用同旁内角互补，两直线平行，分别证明，，即可得到四边形是平行四边形．
【详解】证明：∵五边形是正五边形，
∴，，
∴，
∴，
∴，
∴，
同理，
∴，
，
∴四边形是平行四边形．
【点睛】题目主要考查正多边形内角和定理及等边对等角，三角形内角和定理，平行四边形的判定等，理解题意，综合运用这些知识点是解题关键．
23．（1）见解析（2）见解析
【分析】（1）根据平行四边形的性质，可得AB与CD的关系，根据平行四边形的判定，可得BFDE是平行四边形，再根据矩形的判定，即可证明；
（2）根据平行线的性质，可得∠DFA=∠FAB，根据等腰三角形的判定与性质，可得∠DAF=∠DFA，根据角平分线的判定，即可证明．
【详解】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD．
∵BE∥DF，BE=DF，
∴四边形BFDE是平行四边形．
∵DE⊥AB，
∴∠DEB=90°，
∴四边形BFDE是矩形；
（2）∵四边形ABCD是平行四边形，
∴AB∥DC，
∴∠DFA=∠FAB．
在Rt△BCF中，由勾股定理，得
BC===5，
∴AD=BC=DF=5，
∴∠DAF=∠DFA，
∴∠DAF=∠FAB，
即AF平分∠DAB．
【点睛】本题考查了平行四边形的性质，矩形的判定，等腰三角形的判定与性质，利用等腰三角形的判定与性质得出∠DAF=∠DFA是解题关键．
24．（1）见解析；（2）当BC=CD+AD时，四边形ABED为平行四边形，理由见解析
【分析】（1）依题意∠C′DE=∠CDE，CD=C′D，CE=C′E，又AD∥BC，所以∠C′DE=∠DEC，∠DEC=∠CDE，即CD=CE，则四边相等，可得四边形CDC′E是菱形；
（2）四边形ABED为平行四边形，由题意易证明AD=BE，又AD∥BC，可得AD∥BE，所以四边形ABED为平行四边形可证明AD与BE平行且相等．
【详解】解：
（1）证明：根据题意可得：
CD=C′D，∠C′DE=∠CDE，CE=C′E，
∵AD∥BC，
∴∠C′DE=∠CED，
∴∠CDE=∠CED，
∴CD=CE，
∴CD=C′D=C′E=CE，
∴四边形CDC′E为菱形．
（2）解：当BC=CD+AD时，四边形ABED为平行四边形，
理由：（1）知CE=CD，
又∵BC=CD+AD，
∴BE=AD，
又∵AD∥BC，
∴四边形ABED为平行四边形．
【点睛】本题主要考查了翻折变换，平行四边形的判定，菱形的判定，掌握翻折变换，平行四边形的判定，菱形的判定是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)