第七章实数同步练习（含解析）

中小学教育资源及组卷应用平台
第七章实数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．刘谦的魔术表演风靡全国，小明同学也学起了刘谦发明了一个魔术盒，当任意有理数对（a，b）进入其中时，会得到一个新的有理数：a2+b-1．例如把（3，-2）放入其中，就会得到32+（-2）-1=6．现将有理数对（-1，-2）放入其中，则会得到（　　）
A．-1 B．-2 C．-3 D．2
2．若是正整数，则满足条件的m的最小正整数值为（　　）
A．5 B．6 C．7 D．8
3．估计的值在（ ）
A．1和2之间 B．2和3之间 C．3和4之间 D．4和5之间
4．如图，已知阴影部分是一个正方形，AB=4，∠B=45°，此正方形的面积（ ）
A．16 B．8 C．4 D．2
5． 如图，在Rt△ABC中，∠ACB=90°，BC=3，AC=4，AB的垂直平分线DE交BC的延长线于点E，则CE的长为（ ）
A． B． C． D．2
6．定义，则方程的解为（ ）
A． B． C． D．
7．有下列说法：①负数没有立方根；②一个数的立方根不是正数就是负数；③一个正数或负数的立方根和这个数同号，0的立方根是0；④如果一个数的立方根是这个数本身，那么这个数必是1或0．其中错误的是（ ）
A．①②③ B．①②④ C．②③④ D．①③④
8．立方根等于3的数是（ ）
A．9 B．±9 C．27 D．±27
9．一个正方形的面积为50cm2，则该正方形的边长约为（ ）
A．5cm B．6cm C．7cm D．8 cm
10．一个长方形的长与宽分别是6，3，它的对角线的长可能是（ ）
A．整数 B．分数 C．有理数 D．既不是整数，也不是分数
11．与最接近的两个整数是（ ）
A．1和2 B．2和3 C．3和4 D．4和5
12．如图，在平面直角坐标系中、四边形OABC为菱形，O为原点，A点坐标为（8，0），∠AOC＝60°，则对角线交点E的坐标为（ ）
A．（4，2） B．（2，4） C．（2，6） D．（6，2）
二、填空题
13．如图，在平行四边形ABCD中，将△ABC沿着AC所在的直线折叠得到，交AD于点E，连接，若，，，则的长是 ．
14．已知某数只有一个平方根，那么这个数是 ；若一个数的立方根就是它本身，则这个数是
15．1.若是4的平方根，则 ；若是的立方根，则 ．
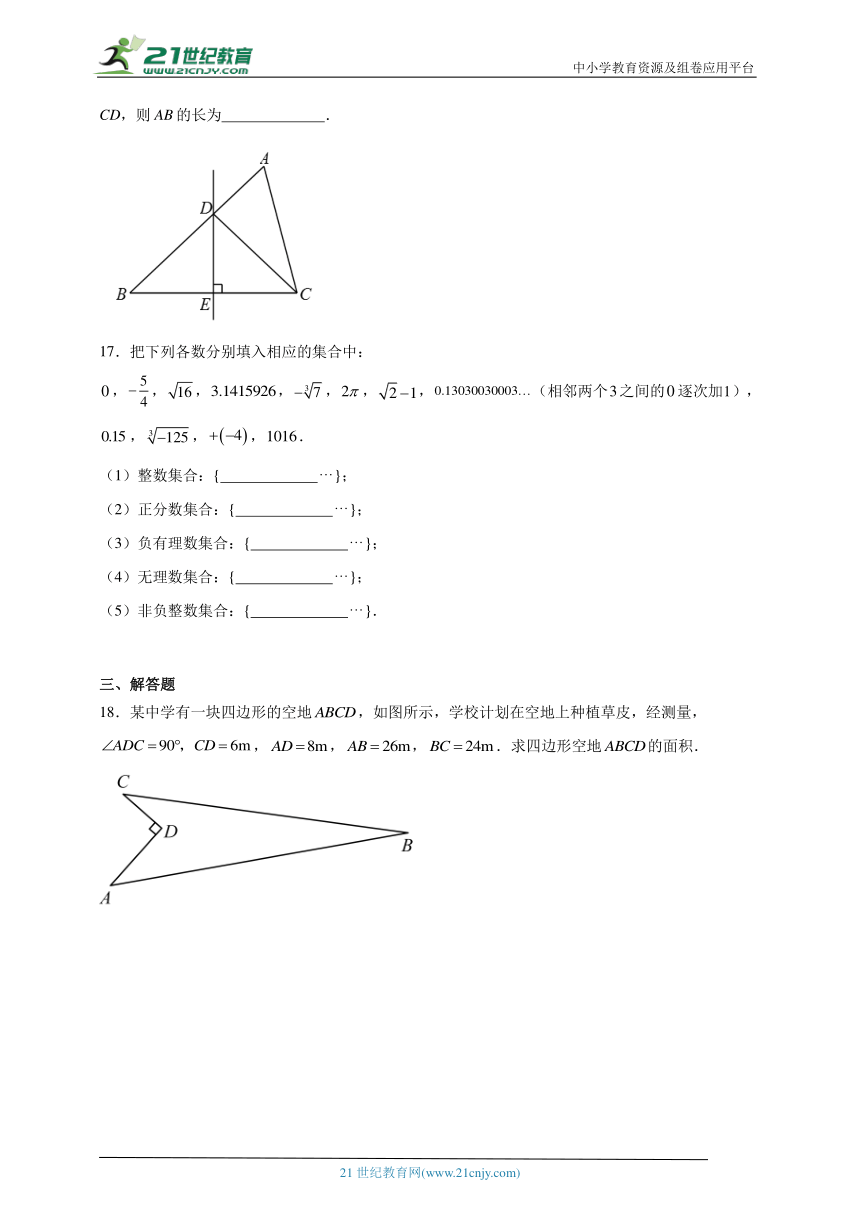
16．如图，在△ABC中，AC＝4，∠A＝60°，∠B＝45°，BC边的垂直平分线DE交AB于点D，连接CD，则AB的长为 ．
17．把下列各数分别填入相应的集合中：
，，，，，，，（相邻两个之间的逐次加），，，，．
（1）整数集合：{ }；
（2）正分数集合：{ }；
（3）负有理数集合：{ }；
（4）无理数集合：{ }；
（5）非负整数集合：{ }．
三、解答题
18．某中学有一块四边形的空地，如图所示，学校计划在空地上种植草皮，经测量，，，，．求四边形空地的面积．
19．（1）采用夹逼法，利用的一系列不足近似值和过剩近似值来估计它的大小的过程如下：
因为，
所以
因为，，
所以
因为，
所以
因为，
所以
因此(精确到百分位)，
使用夹逼法，求出的近似值(精确到百分位)．
（2）我们规定用符号表示数的整数部分，例如
①按此规定 ；
②如果的整数部分是的小数部分是求的值．
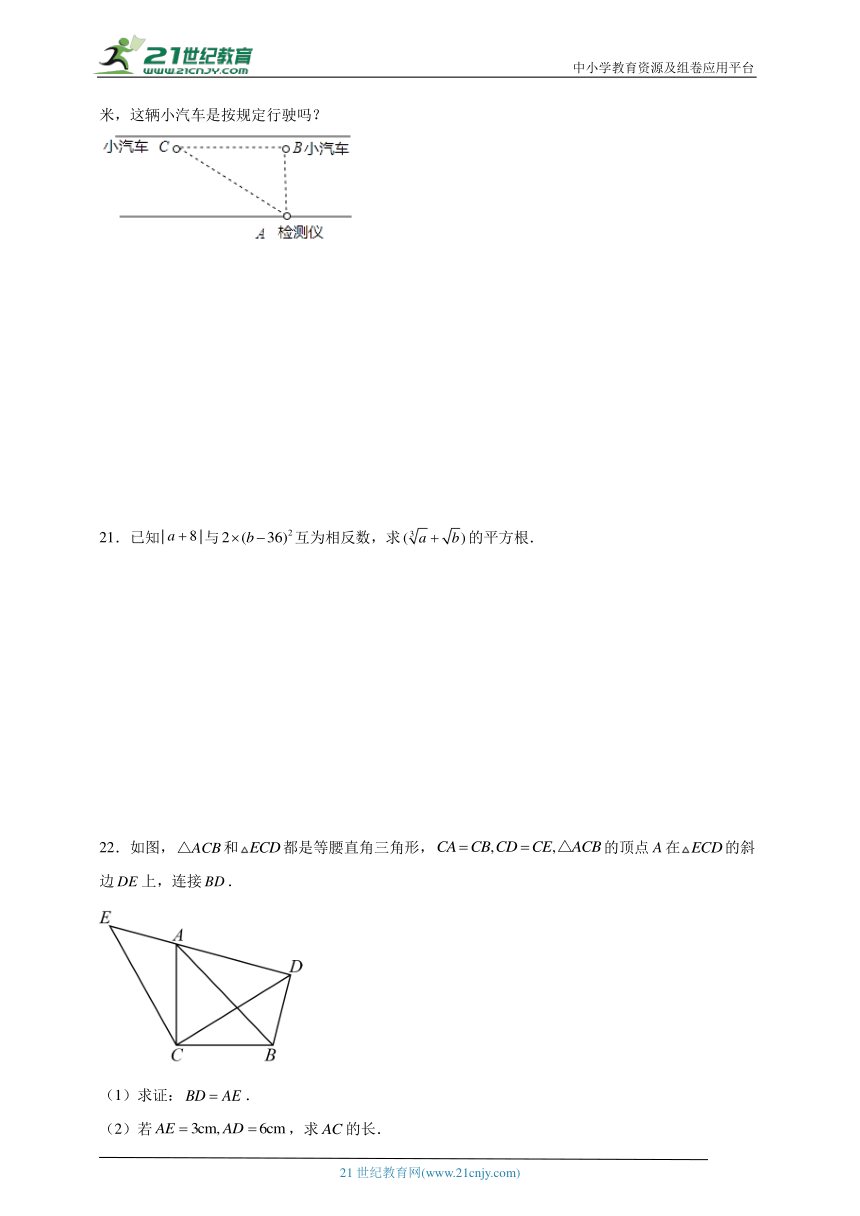
20．“中华人民共和国道路交通管理条例”规定：小汽车在高速公路上的行驶速度不得超过120千米/小时，不得低于60千米/小时，如图，一辆小汽车在高速公路上直道行驶，某一时刻刚好行驶到“车速检测点”正前方60米处，过了3秒后，测得小汽车位置与“车速检测点”之间的距离为100米，这辆小汽车是按规定行驶吗？
21．已知与互为相反数，求的平方根．
22．如图，和都是等腰直角三角形，的顶点A在的斜边上，连接．
（1）求证：．
（2）若，求的长．
23．如图，过圆锥的顶点和底面圆的圆心的平面截圆锥得截面，其中，是圆锥底面圆的直径，已知，，求截面的面积．
24．在矩形中，，点是射线上一个动点，连接并延长交射线于点，将沿直线翻折到，延长与直线交于点．

(1)求证：；
(2)当点是边的中点时，求的长；
(3)当时，求的长．
《第七章实数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B B B B C C D
题号 11 12
答案 C D
1．B
【详解】解：把有理数对（-1，-2）代入a2+b-1=2中得：（-1）2-2-1=1-2-1=-2．故选B．
2．A
【分析】根据算术平方根得出≥0，根据为正整数得出80m是完全平方数，求出即可．
【详解】解：∵为正整数，
∴80m＞0，80m是完全平方数，
∵80×5＝400＝202，
∴m的最小正整数值为：5，
故选：A．
【点睛】本题考查了对算术平方根的应用，注意：a（a≥0）的算术平方根是．
3．C
【分析】本题考查无理数的估算，根据无理数的估算方法得到即可求解．
【详解】解：∵，
∴，则，
故选：C．
4．B
【分析】先利用勾股定理求出正方形的边长，从而得出面积．
【详解】解：∵AB=4，∠B=45°，
∴AC=AB ，，
∴此正方形的面积为
故选B．
5．B
【分析】设CE=x，连接AE，由线段垂直平分线的性质可知AE=BE=BC+CE，在Rt三角形ACE中，利用勾股定理即可求出CE的长度．
【详解】解：设CE=x，连接AE，
∵DE是线段AB的垂直平分线，
∴AE=BE=BC+CE=3+x，
∴在Rt三角形ACE中，AE2=AC2+CE2，即（3+x）2=42+x2，
解得x=．
故答案为B
6．B
【分析】根据新定义,变形方程求解即可
【详解】∵,
∴变形为,
解得 ，
经检验 是原方程的根，
故选B
【点睛】本题考查了新定义问题，根据新定义把方程转化一般的分式方程，并求解是解题的关键
7．B
【分析】根据立方根的定义和性质解答即可．
【详解】解：正数的立方根是正数，负数的立方根是负数，0的立方根是0．立方根等于它本身的数有0，1和．所以①②④都是错误的，③正确.
故选B．
【点睛】本题考查立方根，熟练掌握立方根的定义和性质是解题的关键．
8．C
【详解】∵33＝27，∴27的立方根是3．
故选：C．
9．C
【分析】设正方形的边长是xcm，得出x2＝50，求出即可．
【详解】设正方形的边长是xcm，则x2＝50．
∵x＞0，
∴x≈7．
故选C．
【点睛】本题考查了对正方形性质和算术平方根的应用，关键是根据题意得出方程，注意：方程的解只有一个．
10．D
【分析】长方形的长、宽和对角线，构成一个直角三角形，可用勾股定理，求得对角线的长，再进行选择即可．
【详解】∵，
∴对角线长是无理数．
故选D．
【点睛】本题考查了长方形性质及勾股定理的应用，考查了利用勾股定理解直角三角形的能力以及实数的分类．
11．C
【分析】此题主要考查了利用平方来计算无理数的大小关系．要熟练掌握平方与二次根式之间的计算．
先找到距离11最近的两个完全平方数，即可找到与最接近的两个整数．
【详解】∵
∴与最接近的两个整数是3和4．
故选：C．
12．D
【分析】过点E作EF⊥ x轴于点F，由直角三角形的性质求出EF长和OF长即可．
【详解】解：过点E作EF⊥x轴于点F，
∵四边形OABC为菱形，∠AOC=60°，
∴∠AOE=∠AOC=30°，OB⊥AC，∠FAE=60°，
∴∠AEF=30°
∵A(8,0)，
∴AO=8，
∴AE=AO=×8=4，
∴AF=AE=2，，
∴OF=AO AF=8 2=6，
∴．
故选：D
【点睛】本题考查了菱形的性质、勾股定理及含30°直角三角形的性质，正确作出辅助线是解题的关键．
13．
【分析】根据平行四边形的性质得ADBC，ABCD，可证出∠CAE=45°，∠ADC=60°，根据翻折可得∠ACB′=∠ACB=45°，∠AB′C=∠B=60°，进而可得∠AEC=90°，从而可得AE=CE=3，再根据含30°角的直角三角形的性质求出B′E=DE=，根据勾股定理即可得B′D的长．
【详解】解：∵四边形ABCD是平行四边形，
∴ADBC，ABCD，∠ADC=60°，
∴∠CAE=∠ACB=45°，
∵将△ABC沿AC翻折至△AB′C，
∴∠ACB′=∠ACB=45°，∠AB′C=∠B=60°，
∴∠AEC=180°-∠CAE-∠ACB′=90°，
∴AE=CE=AC=×6=3，
∵∠AEC=90°，∠AB′C=60°，∠ADC=60°，
∴∠B′AD=30°，∠DCE=30°，
∴B′E=AE=×3=，DE=CE=×3=，
∴B′D=．
故答案为：．
【点睛】本题考查平行四边形中的翻折问题，解题的关键是掌握翻折的性质，能熟练应用含30°，45°角的直角三角形三边关系．
14． 0 1，，0
【分析】根据平方根与立方根的性质即可得．
【详解】解：因为一个正数有两个互为相反数的平方根、0的平方根是0、负数没有平方根，
所以已知某数只有一个平方根，那么这个数是0，
因为，，，
所以若一个数的立方根就是它本身，则这个数是1，，0，
故答案为：0；1，，0．
【点睛】本题考查了平方根与立方根，熟练掌握平方根与立方根的性质是解题关键．
15． 1或
【分析】本题主要考查了求一个数的平方根，求一个数的立方根，解题的关键是熟练掌握平方根和立方根定义．根据平方根定义得出，根据立方根定义求出，然后求出x、y的值即可．
【详解】解：∵4的平方根是，
∴，
∴或，
∵的立方根是，
∴，
∴．
故答案为：1或；．
16．2＋2
【分析】根据线段垂直平分线的性质得到DB＝DC，根据三角形的外角性质得到∠ADC＝90°，根据含30°角的直角三角形的性质求出AD，根据勾股定理求出DC，进而求出AB．
【详解】解：∵DE是BC的垂直平分线，
∴DB＝DC，
∴∠DCB＝∠B＝45°，
∴∠ADC＝∠DCB＋∠B＝90°，
∵∠A＝60°，
∴∠ACD＝30°，
∴AD＝AC＝2，
由勾股定理得：DC＝＝＝2，
∴DB＝DC＝2，
∴AB＝AD＋DB＝2＋2，
故答案为：2＋2．
【点睛】本题主要考查了三角形外角性质，线段垂直平分线的性质，直角三角形的性质，勾股定理，熟练掌握相关知识点是解题的关键．
17． ，，，， ， ，， ，，，（相邻两个之间的逐次加） ，，
【分析】本题考查实数的分类，
（1）根据整数的定义选出即可；
（2）根据正数和分数的定义选出即可；
（3）根据负数和有理数的定义选出即可；
（4）根据无理数的定义选出即可；
（5）根据非负整数的定义（即正整数和零）选出即可；
解题的关键是明确实数包括无理数和有理数，无理数包括正无理数和负无理数，有理数包括正有理数，，负有理数．
【详解】解：，，，
（1）整数集合：{，，，，，}，
故答案为：，，，，；
（2）正分数集合：{，，}，
故答案为：，；
（3）负有理数集合：{，，，}，
故答案为：，，；
（4）无理数集合：{，，，（相邻两个之间的逐次加），}，
故答案为：，，，（相邻两个之间的逐次加）；
（5）非负整数集合：{，，，}，
故答案为：，，．
18．四边形空地的面积为．
【分析】本题主要考查了勾股定理和勾股定理的逆定理．如图所示，连接，利用勾股定理求出，进而利用勾股定理的逆定理证明，再根据进行求解即可．
【详解】解：如图所示，连接，
在，
∴，
∵，
∴是直角三角形，即，
∴ （），
答：四边形空地的面积为．
19．（1）；（2）①5，②
【分析】（1）仿照使用夹逼法求近似值的方法解答即可；
（2）①先使用夹逼法确定的范围，然后即可确定的范围，再根据规定解答即可；
②先确定的整数部分a与的小数部分的值，再代入所求式子化简计算即可．
【详解】解：（1）因为，
所以
因为，
所以，
因为，
所以
因为，
所以，
因此．
（2）①因为3.12=9.61，3.22=10.24，
所以，
所以，
所以5；
故答案为：5；
②因为，
所以，
所以原式
．
【点睛】本题考查了利用夹逼法求算术平方根的近似值、对算术平方根的整数和小数部分的认识以及实数的简单计算，属于常考题型，正确理解题意、熟练掌握算术平方根的相关知识是解题关键．
20．这辆小汽车是按“中华人民共和国道路交通管理条例”规定行驶．
【分析】根据勾股定理求出BC，求出速度，再比较即可．
【详解】解：由勾股定理得，（米），
（米/秒），
∵米/秒千米/时，而，
∴这辆小汽车是按“中华人民共和国道路交通管理条例”规定行驶．
【点睛】本题考查了勾股定理的应用，能求出BC的长是解此题的关键．
21．．
【详解】试题分析：利用相反数求和等于0,求出a,b的值.
试题解析：
，
∵，，
∴，，则，．
∴，的平方根为．
22．（1）证明见解析；（2）．
【分析】（1）根据同角的余角相等得出∠BCD=∠ACE，然后根据SAS定理证明△BCD≌△ACE，从而得出结论；
（2）根据全等三角形的性质得出∠BDC=∠AEC，然后结合等腰直角三角形的性质求得∠BDA是直角三角形，从而利用勾股定理求解．
【详解】（1）∵和都是等腰直角三角形，
∴，
∴，
∴，
在和中，
∴，
∴．
（2）∵，
∴，
又∵是等腰直角三角形，
∴，
∴，
∴，
∴是直角三角形，
∴，
在等腰直角三角形中，
，
∴．
【点睛】本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．
23．截面的面积为．
【分析】先利用勾股定理计算出SO，然后根据三角形面积公式求解．
【详解】在中，∵，，
∴，
∴截面的面积．
【点睛】本题考查圆锥的计算,解题关键是熟练掌握圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
24．(1)见解析
(2)
(3)的长为或
【分析】（1）由折叠的性质和平行线的性质及等腰三角形的判定可得出答案；
（2）利用矩形的性质证得，根据全等三角形的性质得到，设，则由（1）知，， ，在中利用勾股定理即可求解；
（3）当时，设，应分两种情况：第一种情况，点在线段上，则，；第二种情况，点在线段的延长线上，则，在中，利用勾股定理即可求解．
【详解】（1）证明：∵四边形为矩形，
∴，
∴，
由折叠可知：，
∴，
∴；
（2）解：∵点E是边的中点，
∴，
∵四边形为矩形，，
∴，，，
∴，
又∵，
∴，
∴，
设，则由（1）知，，，
在中，，
∴，
解得，
∴的长为；
（3）解：当时，设，
第一种情况，点在线段上，如图所示：

则，
∴在中，，
∴，
解得：，
∴的长为；
第二种情况，点在线段的延长线上，如图所示：

则，
∴在中，，
∴，
解得：，
∴的长为；
综上可知，当时，的长为或．
【点睛】本题主要考查了翻折变换，矩形的性质，平行线的性质，等腰三角形的判定，勾股定理，三角形全等的判定和性质，画出图形，数形结合，应用分类讨论的思想是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)