7.4圆锥的侧面展开图同步练习(含解析)
文档属性
| 名称 | 7.4圆锥的侧面展开图同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 836.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 09:59:03 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
7.4圆锥的侧面展开图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB是圆锥的母线,BC为底面半径,已知BC=6cm,圆锥的侧面积为15πcm2,则sin∠ABC的值为( )
A. B. C. D.
2.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是cm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
3.若圆锥的底面半径为2,母线长为5,则圆锥的侧面积为( )
A.5 B.10 C.20 D.40
4.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
5.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径cm,扇形的圆心角为120°,则该圆锥的母线l长为( ).
A.4cm B.5cm C.6cm D.8cm
6.已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于( )
A.8 B.4 C.4 D.8
7.底面直径为6cm的圆锥的侧面展开图的圆心角为216°,则这个圆锥的高为( ).
A.5cm B.3cm C.8cm D.4cm
8.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )
A. B. C. D.
9.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B.1 C. D.4
10.圆锥的母线长为5cm,底面半径为3cm,那么它的侧面展开图的圆心角是( )
A.180° B.200° C.225° D.216°
11.用圆心角为,半径为的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
A. B. C. D.
12.一个几何体的三视图如图所示,这个几何体的侧面积为( )
A.2π cm2 B.4π cm2 C.8π cm2 D.16π cm2
二、填空题
13.填空:
(1)的圆心角所对的弧长是,则此弧所在圆的半径是 ;
(2)一个扇形的弧长是.面积是,则扇形的圆心角是 ;
(3)用一个圆心角为,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
14.若一个圆锥的底面圆的周长是4cm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数是 度.
15.用一个半径为3,圆心角度数为120°的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为 .
16.数学小组要做三个相同的圆锥模型.先用一张直径为60 cm的圆形卡纸,做成了三个侧面(接缝处不计).现在还要三块圆形纸板做底面,那么每块圆形纸板的半径为 cm.
17.已知圆锥的母线长为,侧面积为,则这个圆锥的底面圆半径为 .
三、解答题
18.如图①,已知圆锥的母线长,若以顶点为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角.
(1)求圆锥的底面半径;
(2)求圆锥的全面积.
19.小明和小亮去野炊,带了一顶简易帐篷,帐篷收起来时伞面的长度是4m,撑开后帐篷高2m,求帐篷撑好后的占地面积.
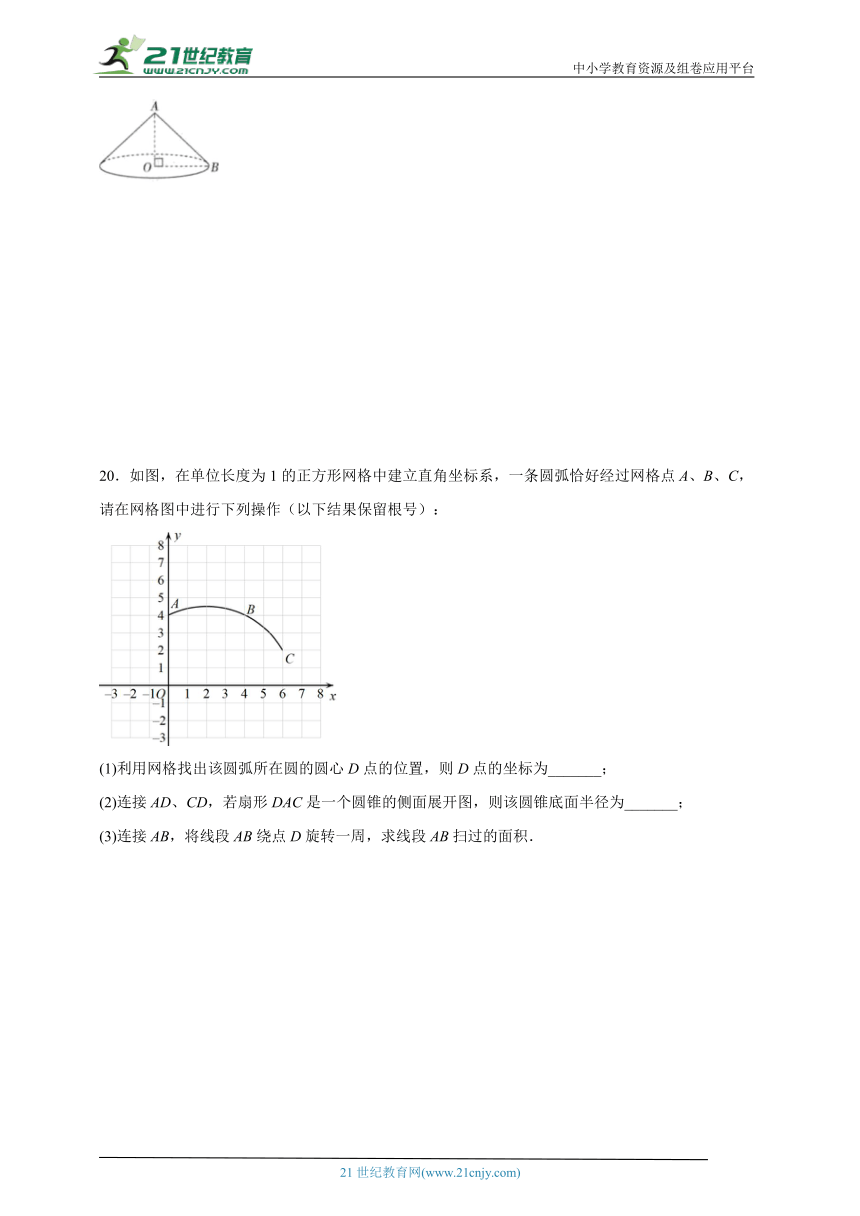
20.如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为_______;
(2)连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为_______;
(3)连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.
21.如图,在中,,,
(1)分别以直线,为轴,把旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线为轴,把旋转一周,求所得几何体的表面积.
22.圆锥的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度.
23.如图,等腰梯形ABCD的上底AD = 4 cm,下底BC = 6 cm,腰长为3 cm,将等腰梯形绕其对称轴旋转180°得一几何体,求这个几何体的侧面积(精确到0.1 cm2).
24.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
《7.4圆锥的侧面展开图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B D C D D C B D
题号 11 12
答案 B B
1.C
【详解】分析:先根据扇形的面积公式S=L R求出母线长,再根据锐角三角函数的定义解答即可.
详解:设圆锥的母线长为R,由题意得
15π=π×3×R,解得R=5,
∴圆锥的高为4,
∴sin∠ABC=.
故选C.
点睛:本题考查了圆锥侧面积公式的运用,注意一个角的正弦值等于这个角的对边与斜边之比.
2.A
【详解】一只扇形的弧长是6πcm,则底面的半径即可求得,底面的半径,圆锥的高以及母线(扇形的半径)正好构成直角三角的三边,利用勾股定理即可求解:
设圆锥的底面半径是r,则2πr=6π,解得:r=3.
则圆锥的高是: (cm).故选A.
3.B
【分析】利用圆锥面积=计算.
【详解】=,
故选:B.
【点睛】此题考查圆锥的侧面积公式,共有三个公式计算圆锥的面积,做题时依据所给的条件恰当选择即可解答.
4.D
【分析】易得圆锥的底面直径与母线长相等,那么根据圆锥的底面周长等于侧面展开图的弧长即可得到这个圆锥的侧面展开图的圆心角度数.
【详解】解:设圆锥的底面半径为r,母线长为R,圆心角的度数为n度
∵它的轴截面是正三角形,∴R=2r,
∴2πr=,
解得n=180,
故展开图的圆心角为180°
故选:D.
【点睛】本题主要考查圆锥的侧面展开图的圆心角,圆锥的轴截面,熟练掌握圆锥的侧面展开图的弧长等于圆锥的底面周长,扇形的弧长公式,是解题的关键.
5.C
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长结合弧长公式列式求解即可.
【详解】解:根据题意得:,
解得:l=6,
即该圆锥母线l的长为6.
故选:C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.D
【分析】根据圆锥的侧面积就等于母线长乘底面周长的一半.依此公式计算即可解决问题.
【详解】解:圆锥的侧面积=π×2×4=8π.
故选D.
【点睛】本题主要考查了圆锥的侧面积的计算公式.熟练掌握圆锥侧面积公式是解题关键.
7.D
【分析】圆锥的展开图为扇形,根据弧长公式l=,以及扇形的弧长就是底面圆的周长,可求出扇形的半径,继而利用勾股定理可求出圆锥的高.
【详解】设扇形的半径为R.由题意得:π×6=,解得:R=5cm ,即AB=5cm,过点A作AD⊥BC与点D.
在Rt△ABD中,AD===4(cm),即圆锥的高为4cm.
故选D.
【点睛】本题考查了圆锥的计算,解答本题的关键是求出圆锥展开图图的扇形的半径,然后利用勾股定理求圆锥的高,难度一般.
8.C
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【详解】此圆锥的侧面积= 4 2π 2=8π.
故选C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
9.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.设这个圆锥的底面圆半径为,利用弧长公式得到,然后解关于的方程即可.
【详解】解:设这个圆锥的底面圆半径为,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故选:B
10.D
【分析】先根据圆的周长公式求得底面圆周长,再根据弧长公式即可求得结果.
【详解】设它的侧面展开图的圆心角是n°,
由题意得底面圆周长=
,
解得n=216
故选D.
【点睛】本题是弧长公式的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.
11.B
【分析】本题主要考查了扇形面积的计算.先求出扇形的弧长,根据扇形的弧长=圆锥的底面周长,用扇形的弧长,可求圆锥的底面半径,利用勾股定理得出答案.
【详解】解:∵扇形的弧长,
∴圆锥的底面半径为,
∴这个圆锥形筒的高为.
故选:B.
12.B
【详解】试题解析:由三视图可知,这个几何体是圆锥.
圆锥的侧面积
故选B.
13. 6 150°
【分析】(1)利用弧长公式进行求解即可;
(2)利用扇形面积公式进行求解即可;
(3)利用圆锥底面圆的周长等于展开图的弧长进行求解即可.
【详解】解:(1)设圆的半径为R,
由题意得:,
解得,
故答案为:6;
(2)设圆的半径为R,圆心角的度数为n,
由题意得:,
解得,
∵,
∴,
故答案为:150°;
(3)设圆锥底面圆的半径为R,
由题意得:,
解得,
故答案为:.
【点睛】本题主要考查了弧长公式,扇形面积公式,圆锥底面圆周长与展开图弧长的关系,解题的关键在于能够熟练掌握相关知识进行求解.
14.120
【分析】根据弧长=圆锥底面周长=4π,圆心角=弧长×180÷母线长÷π计算.
【详解】解:由题意知:弧长=圆锥底面周长=2×2π=4πcm,
扇形的圆心角=弧长×180÷母线长÷π=4π×180÷6π=120°.
故答案为:120.
15.1
【分析】根据弧长公式求出圆锥底面圆的周长,设圆锥的底面圆的半径是R,根据题意得出2πR=2π,再求出R即可.
【详解】解:圆锥底面圆的周长是=2π,
设圆锥的底面圆的半径是R,
则2πR=2π,
解得:R=1,
即该圆锥的底面圆的半径为1,
故答案为:1.
【点睛】本题考查了圆锥的计算和弧长公式,能熟记弧长公式是解此题的关键.
16.10
【分析】设每块圆形纸板的半径为r,根据等量关系:圆形卡纸的周长等于圆锥模型的底面周长的3倍,列出方程,解方程即可.
【详解】解:圆形卡纸的周长为60π cm,
设每块圆形纸板的半径为r,
∴2πr×3=60π,
解得:r=10
故答案为:10.
【点睛】本题考查了圆锥的有关计算,理解题意,准确找到等量关系列出方程是解题的关键.
17.3
【分析】利用圆锥侧面积为rl,代入可求解.
【详解】解:设圆锥的底面半径为rcm,
∵圆锥的母线长是8cm,侧面积是,
∴24= r 8,
∴r=3,
故答案为:3.
【点睛】本题考查了圆锥的计算,解题的关键是正确地进行圆锥与扇形的转化.
18.(1)
(2)
【分析】(1)根据圆锥底面圆周长的3倍=扇形的弧长,构建方程求解即可.
(2)根据表面积=底面积+侧面积,计算即可.
【详解】(1)由题意得:,
∴cm.
(2)圆锥的全面积.
【点睛】本题考查圆锥的计算,弧长公式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
19.
【分析】根据题意可知圆锥的母线长为4米,高2米和地面半径构成直角三角形,利用勾股定理求出底面半径,再求出底面面积.
【详解】解:在中,因为,所以.
所以.
所以.
所以.
故帐篷撑好后的占地面积为
【点睛】主要考查了圆锥的特点.解此题的关键是要知道圆锥的母线,高和地面半径构成直角三角形,利用勾股定理求出底面半径,再求出底面面积,是一个常用的方法.
20.(1)(2,0)
(2)
(3)4π
【分析】(1)线段AB与BC的垂直平分线的交点为D;
(2)连接AC,先判断∠ADC=90°,则可求的弧长,该弧长即为圆锥底面圆的周长,由此可求底面圆的半径;
(3)设AB的中点为E,线段AB的运动轨迹是以D为圆心DA、DE分别为半径的圆环面积.
【详解】(1)解:过点(2,0)作x轴垂线,过点(5,3)作与BC垂直的线,
两线的交点即为D点坐标,
∴D(2,0),
故答案为:(2,0);
(2)解:连接AC,
∵A(0,4),B(4,4),C(6,2),
∴,,,
∵AC2=AD2+CD2,
∴∠ADC=90°,
∴的长,
∵扇形DAC是一个圆锥的侧面展开图,
∴,
∴,
故答案为:;
(3)解:设AB的中点为E,
∴E(2,4),
∴DE=4,
∴S=π×(AD2﹣DE2)=4π,
∴线段AB扫过的面积是4π.
,
【点睛】本题考查圆锥的展开图,垂径定理,能够由三点确定圆的圆心位置,理解圆锥展开图与圆锥各部位的对应关系是解题的关键.
21.(1);
(2) .
【分析】(1)用勾股定理计算出,当以直线为轴把旋转一周得到的圆锥的底面半径是母线长为然后根据圆锥的侧面积公式计算当以直线为轴把旋转一周得到的圆锥的底面半径为母线长为 然后根据圆锥的侧面积公式计算;
(2)作于利用面积法可得到的长,由于以直线为轴把旋转一周所得几何体的是以为底面半径的两个圆锥它的表面积就是两个圆锥的侧面积 圆锥的侧面积公式计算
【详解】(1)解:,,,
∴,
∴以直线为轴,把旋转一周,得到的圆锥的侧面积;
以直线为轴,把旋转一周,得到的圆锥的侧面积;
(2)如答图,过点作于点
∵,
∴,
以直线为轴,把旋转一周,所得几何体是由以为底面半径的两个圆锥组成,
所得几何体的表面积.
【点睛】本题考查了勾股定理,圆锥侧面积的计算,熟练掌握圆锥的侧面积底面半径母线长是解答本题的关键.
22.
【分析】本题主要考查圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【详解】解:将圆锥侧面沿剪开展平,连接,则就是所求绳子长.
由得,
作,则,,
∴,
∴,,
∴.
23.47.1 cm2.
【分析】延长BA,CD交于点S,求出SA的长度,这个几何体的侧面积=半径为SB的扇形面积半径为SA的扇形面积.
【详解】延长BA,CD交于点S,如图所示:
则
则:
即:
解得:
这个几何体的侧面积=
答:这个几何体的侧面积为47.1 cm2.
【点睛】考查圆锥的侧面积的计算,掌握圆锥侧面积的计算公式是解题的关键.
24.(1);(2)
【分析】(1)根据圆锥体积=×底面积×高,进行解答即可得;
(2)根据(1)得出S与d的函数关系进行解答即可得.
【详解】解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
【点睛】本题考查了圆锥的体积,反比例函数的应用,解题的关键是掌握这些知识点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
7.4圆锥的侧面展开图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB是圆锥的母线,BC为底面半径,已知BC=6cm,圆锥的侧面积为15πcm2,则sin∠ABC的值为( )
A. B. C. D.
2.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是cm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
3.若圆锥的底面半径为2,母线长为5,则圆锥的侧面积为( )
A.5 B.10 C.20 D.40
4.圆锥的截面是一个等边三角形,则它的侧面展开图圆心角度数是( )
A.60° B.90° C.120° D.180°
5.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径cm,扇形的圆心角为120°,则该圆锥的母线l长为( ).
A.4cm B.5cm C.6cm D.8cm
6.已知圆锥的母线长为4,底面半径为2,则圆锥的侧面积等于( )
A.8 B.4 C.4 D.8
7.底面直径为6cm的圆锥的侧面展开图的圆心角为216°,则这个圆锥的高为( ).
A.5cm B.3cm C.8cm D.4cm
8.圆锥的母线长为4,底面半径为2,则此圆锥的侧面积是( )
A. B. C. D.
9.用半径为4,圆心角为的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( )
A. B.1 C. D.4
10.圆锥的母线长为5cm,底面半径为3cm,那么它的侧面展开图的圆心角是( )
A.180° B.200° C.225° D.216°
11.用圆心角为,半径为的扇形纸片卷成一个圆锥形无底纸冒(如图所示),则这个纸冒的高是( )
A. B. C. D.
12.一个几何体的三视图如图所示,这个几何体的侧面积为( )
A.2π cm2 B.4π cm2 C.8π cm2 D.16π cm2
二、填空题
13.填空:
(1)的圆心角所对的弧长是,则此弧所在圆的半径是 ;
(2)一个扇形的弧长是.面积是,则扇形的圆心角是 ;
(3)用一个圆心角为,半径为4的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径为 .
14.若一个圆锥的底面圆的周长是4cm,母线长是6cm,则该圆锥的侧面展开图的圆心角的度数是 度.
15.用一个半径为3,圆心角度数为120°的扇形围成一个圆锥的侧面,则该圆锥的底面圆的半径为 .
16.数学小组要做三个相同的圆锥模型.先用一张直径为60 cm的圆形卡纸,做成了三个侧面(接缝处不计).现在还要三块圆形纸板做底面,那么每块圆形纸板的半径为 cm.
17.已知圆锥的母线长为,侧面积为,则这个圆锥的底面圆半径为 .
三、解答题
18.如图①,已知圆锥的母线长,若以顶点为中心,将此圆锥按图②放置在平面上逆时针滚动3圈后所形成的扇形的圆心角.
(1)求圆锥的底面半径;
(2)求圆锥的全面积.
19.小明和小亮去野炊,带了一顶简易帐篷,帐篷收起来时伞面的长度是4m,撑开后帐篷高2m,求帐篷撑好后的占地面积.
20.如图,在单位长度为1的正方形网格中建立直角坐标系,一条圆弧恰好经过网格点A、B、C,请在网格图中进行下列操作(以下结果保留根号):
(1)利用网格找出该圆弧所在圆的圆心D点的位置,则D点的坐标为_______;
(2)连接AD、CD,若扇形DAC是一个圆锥的侧面展开图,则该圆锥底面半径为_______;
(3)连接AB,将线段AB绕点D旋转一周,求线段AB扫过的面积.
21.如图,在中,,,
(1)分别以直线,为轴,把旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;
(2)以直线为轴,把旋转一周,求所得几何体的表面积.
22.圆锥的底面半径是3,母线长是9,P是底面圆周上一点:从点P拉一根绳子绕圆锥侧面一周,再回到P点,求这根绳子的最短长度.
23.如图,等腰梯形ABCD的上底AD = 4 cm,下底BC = 6 cm,腰长为3 cm,将等腰梯形绕其对称轴旋转180°得一几何体,求这个几何体的侧面积(精确到0.1 cm2).
24.如图,某玻璃器皿制造公司要制造一种容积为()的圆锥形漏斗.
(1)漏斗口的面积S(单位:)与漏斗的深d(单位:)有怎样的函数关系?
(2)如果漏斗口的面积为,那么漏斗的深为多少?
《7.4圆锥的侧面展开图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B D C D D C B D
题号 11 12
答案 B B
1.C
【详解】分析:先根据扇形的面积公式S=L R求出母线长,再根据锐角三角函数的定义解答即可.
详解:设圆锥的母线长为R,由题意得
15π=π×3×R,解得R=5,
∴圆锥的高为4,
∴sin∠ABC=.
故选C.
点睛:本题考查了圆锥侧面积公式的运用,注意一个角的正弦值等于这个角的对边与斜边之比.
2.A
【详解】一只扇形的弧长是6πcm,则底面的半径即可求得,底面的半径,圆锥的高以及母线(扇形的半径)正好构成直角三角的三边,利用勾股定理即可求解:
设圆锥的底面半径是r,则2πr=6π,解得:r=3.
则圆锥的高是: (cm).故选A.
3.B
【分析】利用圆锥面积=计算.
【详解】=,
故选:B.
【点睛】此题考查圆锥的侧面积公式,共有三个公式计算圆锥的面积,做题时依据所给的条件恰当选择即可解答.
4.D
【分析】易得圆锥的底面直径与母线长相等,那么根据圆锥的底面周长等于侧面展开图的弧长即可得到这个圆锥的侧面展开图的圆心角度数.
【详解】解:设圆锥的底面半径为r,母线长为R,圆心角的度数为n度
∵它的轴截面是正三角形,∴R=2r,
∴2πr=,
解得n=180,
故展开图的圆心角为180°
故选:D.
【点睛】本题主要考查圆锥的侧面展开图的圆心角,圆锥的轴截面,熟练掌握圆锥的侧面展开图的弧长等于圆锥的底面周长,扇形的弧长公式,是解题的关键.
5.C
【分析】利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长结合弧长公式列式求解即可.
【详解】解:根据题意得:,
解得:l=6,
即该圆锥母线l的长为6.
故选:C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
6.D
【分析】根据圆锥的侧面积就等于母线长乘底面周长的一半.依此公式计算即可解决问题.
【详解】解:圆锥的侧面积=π×2×4=8π.
故选D.
【点睛】本题主要考查了圆锥的侧面积的计算公式.熟练掌握圆锥侧面积公式是解题关键.
7.D
【分析】圆锥的展开图为扇形,根据弧长公式l=,以及扇形的弧长就是底面圆的周长,可求出扇形的半径,继而利用勾股定理可求出圆锥的高.
【详解】设扇形的半径为R.由题意得:π×6=,解得:R=5cm ,即AB=5cm,过点A作AD⊥BC与点D.
在Rt△ABD中,AD===4(cm),即圆锥的高为4cm.
故选D.
【点睛】本题考查了圆锥的计算,解答本题的关键是求出圆锥展开图图的扇形的半径,然后利用勾股定理求圆锥的高,难度一般.
8.C
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【详解】此圆锥的侧面积= 4 2π 2=8π.
故选C.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
9.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.设这个圆锥的底面圆半径为,利用弧长公式得到,然后解关于的方程即可.
【详解】解:设这个圆锥的底面圆半径为,
根据题意得,
解得,
所以这个圆锥的底面圆半径为1.
故选:B
10.D
【分析】先根据圆的周长公式求得底面圆周长,再根据弧长公式即可求得结果.
【详解】设它的侧面展开图的圆心角是n°,
由题意得底面圆周长=
,
解得n=216
故选D.
【点睛】本题是弧长公式的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,难度一般.
11.B
【分析】本题主要考查了扇形面积的计算.先求出扇形的弧长,根据扇形的弧长=圆锥的底面周长,用扇形的弧长,可求圆锥的底面半径,利用勾股定理得出答案.
【详解】解:∵扇形的弧长,
∴圆锥的底面半径为,
∴这个圆锥形筒的高为.
故选:B.
12.B
【详解】试题解析:由三视图可知,这个几何体是圆锥.
圆锥的侧面积
故选B.
13. 6 150°
【分析】(1)利用弧长公式进行求解即可;
(2)利用扇形面积公式进行求解即可;
(3)利用圆锥底面圆的周长等于展开图的弧长进行求解即可.
【详解】解:(1)设圆的半径为R,
由题意得:,
解得,
故答案为:6;
(2)设圆的半径为R,圆心角的度数为n,
由题意得:,
解得,
∵,
∴,
故答案为:150°;
(3)设圆锥底面圆的半径为R,
由题意得:,
解得,
故答案为:.
【点睛】本题主要考查了弧长公式,扇形面积公式,圆锥底面圆周长与展开图弧长的关系,解题的关键在于能够熟练掌握相关知识进行求解.
14.120
【分析】根据弧长=圆锥底面周长=4π,圆心角=弧长×180÷母线长÷π计算.
【详解】解:由题意知:弧长=圆锥底面周长=2×2π=4πcm,
扇形的圆心角=弧长×180÷母线长÷π=4π×180÷6π=120°.
故答案为:120.
15.1
【分析】根据弧长公式求出圆锥底面圆的周长,设圆锥的底面圆的半径是R,根据题意得出2πR=2π,再求出R即可.
【详解】解:圆锥底面圆的周长是=2π,
设圆锥的底面圆的半径是R,
则2πR=2π,
解得:R=1,
即该圆锥的底面圆的半径为1,
故答案为:1.
【点睛】本题考查了圆锥的计算和弧长公式,能熟记弧长公式是解此题的关键.
16.10
【分析】设每块圆形纸板的半径为r,根据等量关系:圆形卡纸的周长等于圆锥模型的底面周长的3倍,列出方程,解方程即可.
【详解】解:圆形卡纸的周长为60π cm,
设每块圆形纸板的半径为r,
∴2πr×3=60π,
解得:r=10
故答案为:10.
【点睛】本题考查了圆锥的有关计算,理解题意,准确找到等量关系列出方程是解题的关键.
17.3
【分析】利用圆锥侧面积为rl,代入可求解.
【详解】解:设圆锥的底面半径为rcm,
∵圆锥的母线长是8cm,侧面积是,
∴24= r 8,
∴r=3,
故答案为:3.
【点睛】本题考查了圆锥的计算,解题的关键是正确地进行圆锥与扇形的转化.
18.(1)
(2)
【分析】(1)根据圆锥底面圆周长的3倍=扇形的弧长,构建方程求解即可.
(2)根据表面积=底面积+侧面积,计算即可.
【详解】(1)由题意得:,
∴cm.
(2)圆锥的全面积.
【点睛】本题考查圆锥的计算,弧长公式等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.
19.
【分析】根据题意可知圆锥的母线长为4米,高2米和地面半径构成直角三角形,利用勾股定理求出底面半径,再求出底面面积.
【详解】解:在中,因为,所以.
所以.
所以.
所以.
故帐篷撑好后的占地面积为
【点睛】主要考查了圆锥的特点.解此题的关键是要知道圆锥的母线,高和地面半径构成直角三角形,利用勾股定理求出底面半径,再求出底面面积,是一个常用的方法.
20.(1)(2,0)
(2)
(3)4π
【分析】(1)线段AB与BC的垂直平分线的交点为D;
(2)连接AC,先判断∠ADC=90°,则可求的弧长,该弧长即为圆锥底面圆的周长,由此可求底面圆的半径;
(3)设AB的中点为E,线段AB的运动轨迹是以D为圆心DA、DE分别为半径的圆环面积.
【详解】(1)解:过点(2,0)作x轴垂线,过点(5,3)作与BC垂直的线,
两线的交点即为D点坐标,
∴D(2,0),
故答案为:(2,0);
(2)解:连接AC,
∵A(0,4),B(4,4),C(6,2),
∴,,,
∵AC2=AD2+CD2,
∴∠ADC=90°,
∴的长,
∵扇形DAC是一个圆锥的侧面展开图,
∴,
∴,
故答案为:;
(3)解:设AB的中点为E,
∴E(2,4),
∴DE=4,
∴S=π×(AD2﹣DE2)=4π,
∴线段AB扫过的面积是4π.
,
【点睛】本题考查圆锥的展开图,垂径定理,能够由三点确定圆的圆心位置,理解圆锥展开图与圆锥各部位的对应关系是解题的关键.
21.(1);
(2) .
【分析】(1)用勾股定理计算出,当以直线为轴把旋转一周得到的圆锥的底面半径是母线长为然后根据圆锥的侧面积公式计算当以直线为轴把旋转一周得到的圆锥的底面半径为母线长为 然后根据圆锥的侧面积公式计算;
(2)作于利用面积法可得到的长,由于以直线为轴把旋转一周所得几何体的是以为底面半径的两个圆锥它的表面积就是两个圆锥的侧面积 圆锥的侧面积公式计算
【详解】(1)解:,,,
∴,
∴以直线为轴,把旋转一周,得到的圆锥的侧面积;
以直线为轴,把旋转一周,得到的圆锥的侧面积;
(2)如答图,过点作于点
∵,
∴,
以直线为轴,把旋转一周,所得几何体是由以为底面半径的两个圆锥组成,
所得几何体的表面积.
【点睛】本题考查了勾股定理,圆锥侧面积的计算,熟练掌握圆锥的侧面积底面半径母线长是解答本题的关键.
22.
【分析】本题主要考查圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.
圆锥的侧面展开图是扇形,从A点出发绕侧面一周,再回到A点的最短的路线即展开得到的扇形的弧所对直径,转化为求直径的长的问题.
【详解】解:将圆锥侧面沿剪开展平,连接,则就是所求绳子长.
由得,
作,则,,
∴,
∴,,
∴.
23.47.1 cm2.
【分析】延长BA,CD交于点S,求出SA的长度,这个几何体的侧面积=半径为SB的扇形面积半径为SA的扇形面积.
【详解】延长BA,CD交于点S,如图所示:
则
则:
即:
解得:
这个几何体的侧面积=
答:这个几何体的侧面积为47.1 cm2.
【点睛】考查圆锥的侧面积的计算,掌握圆锥侧面积的计算公式是解题的关键.
24.(1);(2)
【分析】(1)根据圆锥体积=×底面积×高,进行解答即可得;
(2)根据(1)得出S与d的函数关系进行解答即可得.
【详解】解:(1)根据圆锥体积=×底面积×高,得,
则,
故漏斗口的面积S与漏斗的深度d之间的函数关系为:;
(2)∵S=100cm2=1dm2,
∴,
解得d=3dm=30cm,
故漏斗口的面积为100cm2,那么漏斗的深为30cm.
【点睛】本题考查了圆锥的体积,反比例函数的应用,解题的关键是掌握这些知识点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
