第八章投影与识图同步练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第八章投影与识图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
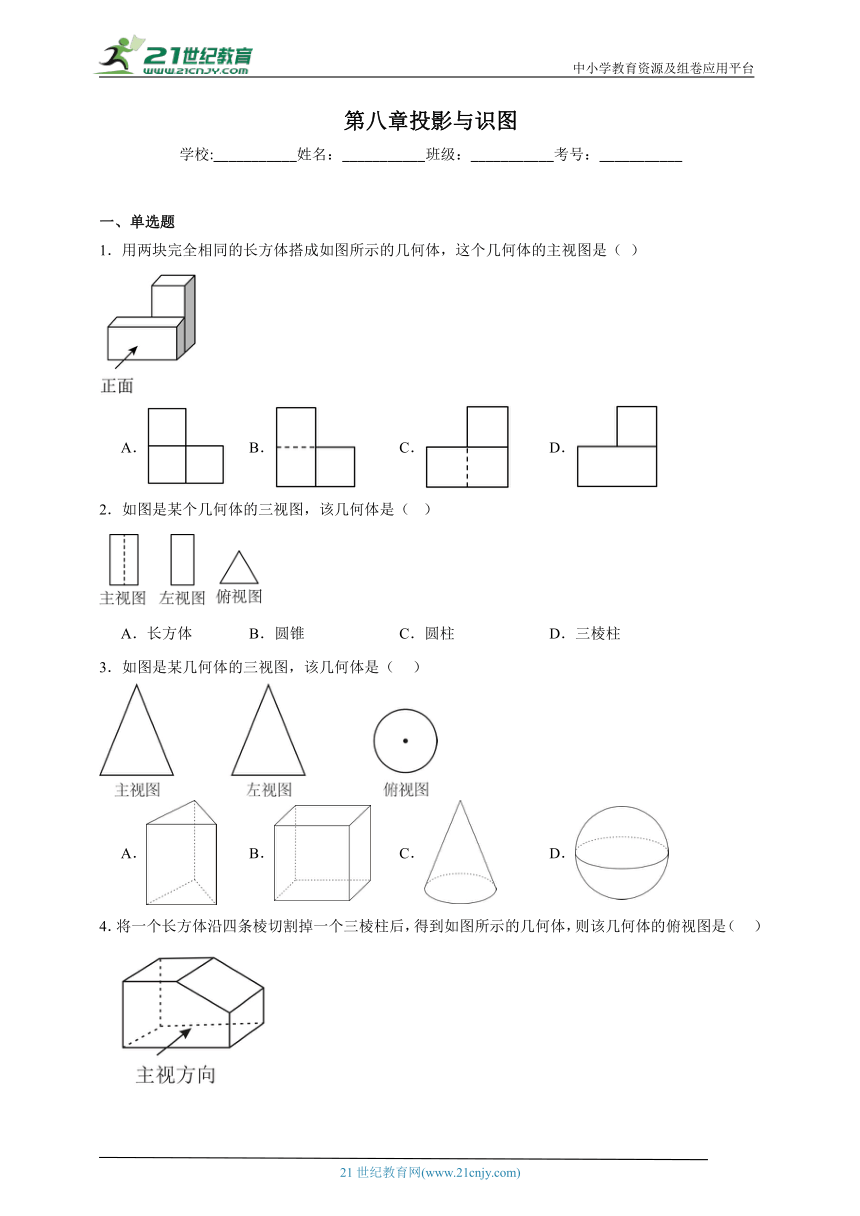
1.用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )
A. B. C. D.
2.如图是某个几何体的三视图,该几何体是( )
A.长方体 B.圆锥 C.圆柱 D.三棱柱
3.如图是某几何体的三视图,该几何体是( )
A. B. C. D.
4.将一个长方体沿四条棱切割掉一个三棱柱后,得到如图所示的几何体,则该几何体的俯视图是( )
A. B. C. D.
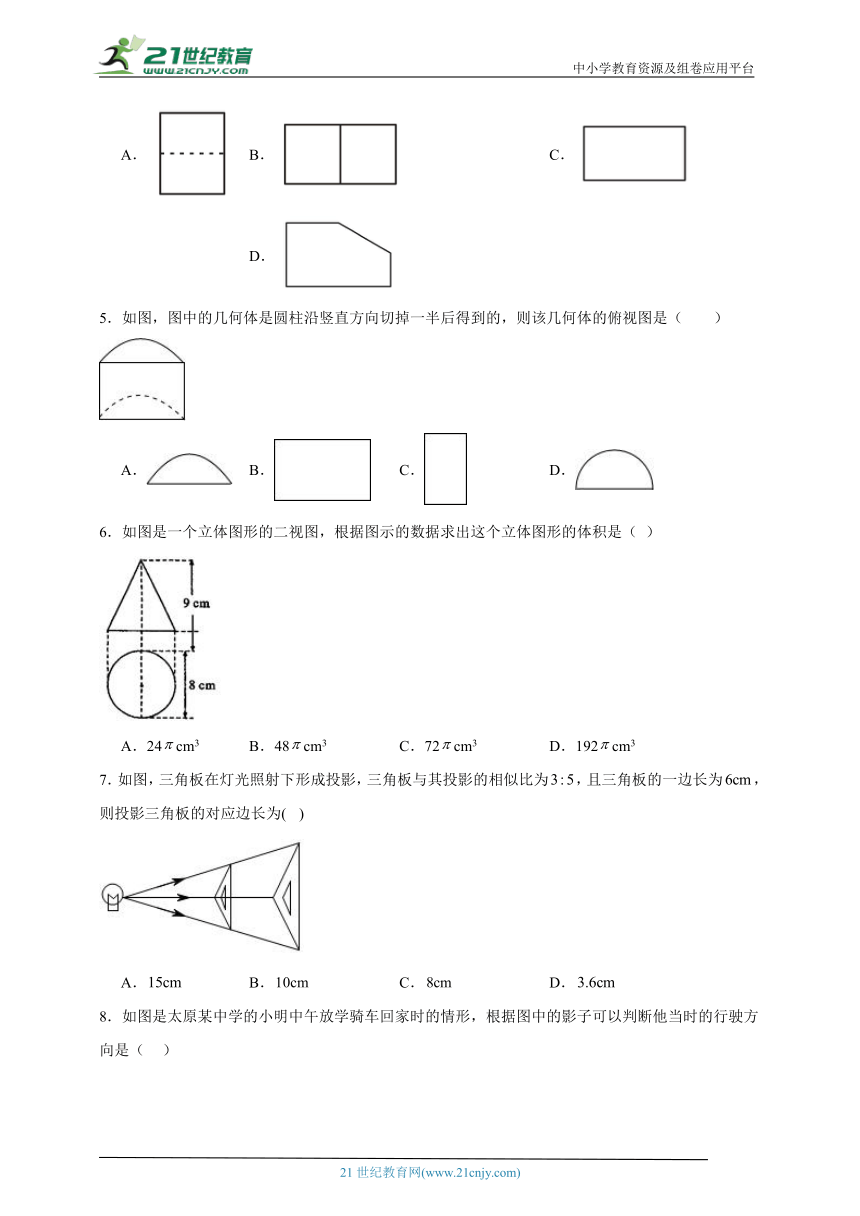
5.如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
A. B. C. D.
6.如图是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是( )
A.24cm3 B.48cm3 C.72cm3 D.192cm3
7.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为,且三角板的一边长为,则投影三角板的对应边长为( )
A. B. C. D.
8.如图是太原某中学的小明中午放学骑车回家时的情形,根据图中的影子可以判断他当时的行驶方向是( )
A.向东 B.向西 C.向南 D.向北
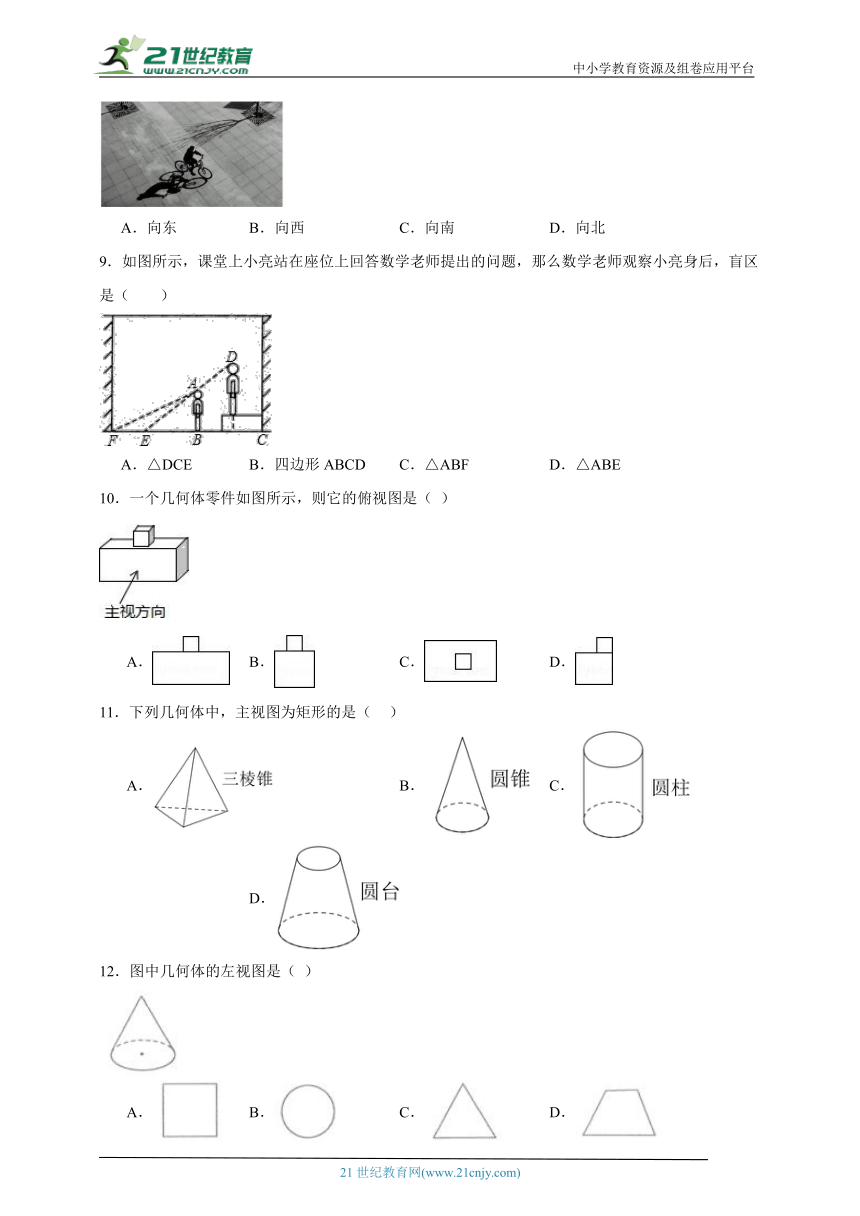
9.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE B.四边形ABCD C.△ABF D.△ABE
10.一个几何体零件如图所示,则它的俯视图是( )
A. B. C. D.
11.下列几何体中,主视图为矩形的是( )
A. B. C. D.
12.图中几何体的左视图是( )
A. B. C. D.
二、填空题
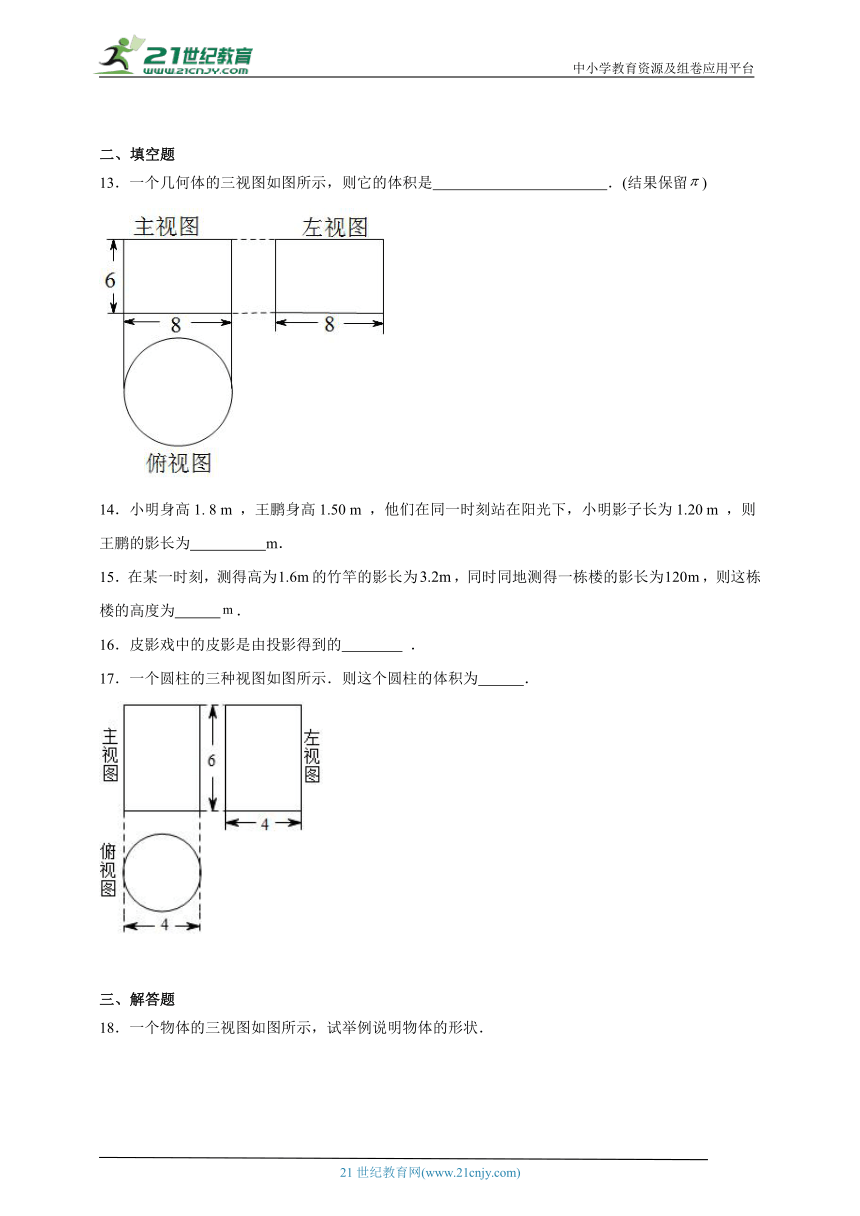
13.一个几何体的三视图如图所示,则它的体积是 .(结果保留)
14.小明身高1. 8 m ,王鹏身高1.50 m ,他们在同一时刻站在阳光下,小明影子长为1.20 m ,则王鹏的影长为 m.
15.在某一时刻,测得高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为 .
16.皮影戏中的皮影是由投影得到的 .
17.一个圆柱的三种视图如图所示.则这个圆柱的体积为 .
三、解答题
18.一个物体的三视图如图所示,试举例说明物体的形状.
19.画出如图所示几何体的三视图.
20.如图,为一盏路灯的灯杆,已知该路灯的灯泡P位于灯杆上,地面上竖立着一个矩形单杠,已知单杠右侧杆在路灯灯泡P的照射下的影子末端位于点E处,已知O、B、C、E在一条直线上,且,,.
(1)请在图中找出路灯灯泡P的位置,并画出单杠左侧杆在灯泡P的照射下的影子;
(2)经测量米,米,单杠的高度米,请你计算路灯灯泡距地面的高度.
21.画出下列几何体的三视图.
22.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
23.一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和左面看到的这个几何体的形状图.
24.如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图;(用阴影表示)
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
《第八章投影与识图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B D B B C D C
题号 11 12
答案 C C
1.C
【分析】根据主视图的定义,找到从正面看所得到的图形即可.
【详解】从物体正面看,左边1列、右边1列上下各一个正方形,且左右正方形中间是虚线,
故选C.
2.D
【分析】本题主要考查了几何体的三视图,熟练掌握几何体的三视图的定义是解题关键.根据几何体的三视图,判断出几何体即可.
【详解】解:俯视图是三角形的,因此这个几何体的上面、下面是三角形的,主视图和左视图是长方形的,且左视图的长方形的宽较窄,因此判断这个几何体是三棱柱.
故选:D.
3.C
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:主视图和左视图都是等腰三角形,那么此几何体为锥体,由俯视图为圆,可得此几何体是圆锥.
故选:C.
【点睛】本题考查了由三视图判断几何体,主视图和左视图的大致轮廓为三角形的几何体为锥体.
4.B
【分析】根据几何体三视图的判断方法解答.
【详解】
解:这个几何体的俯视图为
故选:B.
【点睛】此题考查了简单几何体的三视图的判断,正确理解俯视图为从上方看物体是解题的关键.
5.D
【分析】俯视图是从物体上面看所得到的图形.
【详解】从几何体的上面看俯视图是
,
故选D.
6.B
【详解】本题考查的是由三视图判断几何体
该图形的正视图为三角形,俯视图为圆形,则该图形是一个圆锥体,根据圆锥的体积公式即可求得结果.
易得该几何体为圆锥,圆的直径为8cm,高9cm,则,故选B.
7.B
【分析】中心投影下的三角板与投影三角板一定是相似的,再根据相似三角形对应边的比等于相似比,列式进行计算即可.
【详解】解:三角板的一边长为,则设投影三角板的对应边长为,
三角板与其投影的相似比为,
,
,
投影三角板的对应边长为.
故选:B.
【点睛】此题主要考查了中心投影与相似三角形的性质,熟练掌握中心投影的概念与相似三角形的性质是解答此题的关键.
8.C
【分析】根据影子的位置,再结合阳光的方向进行判断即可.
【详解】解:中午放学时太阳光线由东向西,
所以可判断小明当时的行驶方向是由北向南.
故选:C.
【点睛】本题考查了方位角和投影;结合阳光方向和影子方向确定行驶方向是解决问题的关键.
9.D
【详解】盲区就是看不到的地区,观察图形可解决.
解:根据盲区的定义,位于D的视点的盲区应该是三角形ABE的区域.
故选D.
10.C
【详解】试题分析:这个几何体零件的俯视图是一个正中间有一个小正方形的矩形,
所以它的俯视图是选项C中的图形.
故选C.
考点:简单组合体的三视图.
11.C
【分析】根据常见几何体的主视图,依次判断即可.
【详解】A.该三棱锥的主视图为中间有条线段的三角形,故不符合题意;
B.该圆锥的主视图为三角形,故不符合题意;
C.该圆柱的主视图为矩形,故符合题意;
D.该圆台的主视图为梯形,故不符合题意;
故选:C.
【点睛】本题考查常见几何体的三视图,掌握常见几何体的三视图是解答本题的关键.
12.C
【分析】圆锥的左视图就是从圆锥的左边看即可得到答案.
【详解】解:从圆锥的左边看可以看到一个等腰三角形.
故选C.
【点睛】本题考查了简单几何体的三视图,左视图是从几何体的左边看所得到的图形.
13.
【分析】根据几何体的三视图,得出该几何体为圆柱体,其底面直径为8,高为6,从而求出圆柱体体积.
【详解】解:由三视图可得,该几何体是一个底面直径为8,高为6的圆柱体,
∴该几何体的体积为:
故答案为:
【点睛】本题考查了利用三视图求空间几何体的体积的应用问题,是基础题目.
14.1
【详解】解:设王鹏的影长为xm,因为同一时刻在阳光下的物体的高与影长成比例,所以所以x=1
故答案为:1.
【点睛】本题考查成比例线段,正确列出比例式是解题关键.
15.60
【分析】本题考查平行投影,熟练掌握平行投影是解题的关键.设这栋楼的高度为,根据题意可列出关于x的方程,求解即可.
【详解】解:设这栋楼的高度为,
根据题意有:,
解得:,
故这栋楼的高度为.
故答案为:.
16.中心投影
【详解】考点:中心投影.
分析:皮影戏是有灯光照射下在影布上形成的投影,故是中心投影.
解答:解:皮影戏是有灯光照射下在影布上形成的投影,故是中心投影.
点评:本题属于基础题,考查了投影的知识,可运用投影的知识或直接联系生活实际解答.
17.24π
【分析】根据主视图确定圆柱的高为6,根据俯视图确定圆的直径为4即半径为2,利用公式计算即可.
【详解】∵
∴圆柱的高为6,圆的直径为4即半径为2,
∴圆柱的体积为==24π,
故答案为:24π.
【点睛】本题考查了圆柱的三视图,圆柱的体积,熟练读懂三视图,确定圆柱的高和直径是解题的关键.
18.该几何体是实心圆台.
【分析】根据此几何体的俯视图是圆环,主视图和左视图均是等腰梯形可知该几何体为实心圆台,然后作出图形即可.
【详解】∵此几何体的俯视图是圆环,主视图和左视图均是等腰梯形,∴该几何体是实心圆台,∴其形状为:实心圆台.
【点睛】本题考查了由三视图判断几何体的知识,由几何体的俯视图可确定该几何体的主视图和左视图,要熟练掌握.
19.见解析
【分析】主视图和左视图都是等腰梯形,俯视图是圆环,依此画出即可;
【详解】如图所示.
依次为主视图、左视图、俯视图
【点睛】考查了作图-三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
20.(1)见解析
(2)米
【分析】(1)连接并延长交于点P,连接并延长交于F,点P和即为所求;
(2)先求出米,证明,得到,即,则米.
【详解】(1)解:如图所示,点P和即为所求;
(2)解:∵米,米,
∴米,
∵,,即,
∴,
∴,即,
∴米,
∴路灯灯泡距地面的高度为米.
【点睛】本题主要考查了相似三角形的应用举例,熟知相似三角形的性质与判定条件是解题的关键.
21.见解析
【详解】如图,
22.组成这个几何体的小正方体的个数是8个或9个或10个.
【分析】根据三视图,可知该几何体共有两列三行组成,底面有5个正方体,第二层最少有2个最多有4个正方体,第三层有1个,相加即可求解.
【详解】该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,
5+2+1=8(个),
5+4+1=10(个).
答:组成这个几何体的小正方体的个数是8个或9个或10个.
【点睛】本题考查由三视图判断几何体,根据题目中要求的可能有多少个小正方体搭建这个几何体,根据“俯视图打地基,正视图疯狂盖,左视图拆违章”很容易就知道小正方体的个数,一定要将所有可能性考虑全面.
23.见解析
【分析】本题主要考查从不同方向看几何体.根据题意可得,从正面看有3列,每列小正方数形数目分别为3,1,4;从左面看有3列,每列小正方形数目分别为2,4,3.据此可画出图形,即可.
【详解】解:如图所示:
24.(1)见解析
(2) 4
【分析】(1)由已知条件可知,左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1,据此可画出图形.
(2)可在最底层第二列第三行加一个,第三列第二行加2个,第三列第三行加1个,共4个.
【详解】(1)画图如下:
(2)最多可再添加4个小正方体.
在第2层的第2行第2列和第3行第2列各添加1个小立方块,第3层的第3行第2列和第3行第3列各添加1个小立方块,这个几何体的俯视图和左视图不变,,故最多可再添加4个小立方块.
【点睛】本题考查三视图的画法,以及根据三视图求立方体个数,属于中等难度题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第八章投影与识图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用两块完全相同的长方体搭成如图所示的几何体,这个几何体的主视图是( )
A. B. C. D.
2.如图是某个几何体的三视图,该几何体是( )
A.长方体 B.圆锥 C.圆柱 D.三棱柱
3.如图是某几何体的三视图,该几何体是( )
A. B. C. D.
4.将一个长方体沿四条棱切割掉一个三棱柱后,得到如图所示的几何体,则该几何体的俯视图是( )
A. B. C. D.
5.如图,图中的几何体是圆柱沿竖直方向切掉一半后得到的,则该几何体的俯视图是( )
A. B. C. D.
6.如图是一个立体图形的二视图,根据图示的数据求出这个立体图形的体积是( )
A.24cm3 B.48cm3 C.72cm3 D.192cm3
7.如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为,且三角板的一边长为,则投影三角板的对应边长为( )
A. B. C. D.
8.如图是太原某中学的小明中午放学骑车回家时的情形,根据图中的影子可以判断他当时的行驶方向是( )
A.向东 B.向西 C.向南 D.向北
9.如图所示,课堂上小亮站在座位上回答数学老师提出的问题,那么数学老师观察小亮身后,盲区是( )
A.△DCE B.四边形ABCD C.△ABF D.△ABE
10.一个几何体零件如图所示,则它的俯视图是( )
A. B. C. D.
11.下列几何体中,主视图为矩形的是( )
A. B. C. D.
12.图中几何体的左视图是( )
A. B. C. D.
二、填空题
13.一个几何体的三视图如图所示,则它的体积是 .(结果保留)
14.小明身高1. 8 m ,王鹏身高1.50 m ,他们在同一时刻站在阳光下,小明影子长为1.20 m ,则王鹏的影长为 m.
15.在某一时刻,测得高为的竹竿的影长为,同时同地测得一栋楼的影长为,则这栋楼的高度为 .
16.皮影戏中的皮影是由投影得到的 .
17.一个圆柱的三种视图如图所示.则这个圆柱的体积为 .
三、解答题
18.一个物体的三视图如图所示,试举例说明物体的形状.
19.画出如图所示几何体的三视图.
20.如图,为一盏路灯的灯杆,已知该路灯的灯泡P位于灯杆上,地面上竖立着一个矩形单杠,已知单杠右侧杆在路灯灯泡P的照射下的影子末端位于点E处,已知O、B、C、E在一条直线上,且,,.
(1)请在图中找出路灯灯泡P的位置,并画出单杠左侧杆在灯泡P的照射下的影子;
(2)经测量米,米,单杠的高度米,请你计算路灯灯泡距地面的高度.
21.画出下列几何体的三视图.
22.有一些大小相同的小正方体组成的简单几何体,从不同方向看到的平面图形如图所示,请你猜一猜组成这个几何体的小正方体的个数.
23.一个几何体由若干个大小相同的小立方块搭成,从上面看到的几何体的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数.请画出从正面和左面看到的这个几何体的形状图.
24.如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的左视图和俯视图;(用阴影表示)
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的俯视图和左视图不变,那么最多可以再添加几个小正方体?
《第八章投影与识图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B D B B C D C
题号 11 12
答案 C C
1.C
【分析】根据主视图的定义,找到从正面看所得到的图形即可.
【详解】从物体正面看,左边1列、右边1列上下各一个正方形,且左右正方形中间是虚线,
故选C.
2.D
【分析】本题主要考查了几何体的三视图,熟练掌握几何体的三视图的定义是解题关键.根据几何体的三视图,判断出几何体即可.
【详解】解:俯视图是三角形的,因此这个几何体的上面、下面是三角形的,主视图和左视图是长方形的,且左视图的长方形的宽较窄,因此判断这个几何体是三棱柱.
故选:D.
3.C
【分析】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.
【详解】解:主视图和左视图都是等腰三角形,那么此几何体为锥体,由俯视图为圆,可得此几何体是圆锥.
故选:C.
【点睛】本题考查了由三视图判断几何体,主视图和左视图的大致轮廓为三角形的几何体为锥体.
4.B
【分析】根据几何体三视图的判断方法解答.
【详解】
解:这个几何体的俯视图为
故选:B.
【点睛】此题考查了简单几何体的三视图的判断,正确理解俯视图为从上方看物体是解题的关键.
5.D
【分析】俯视图是从物体上面看所得到的图形.
【详解】从几何体的上面看俯视图是
,
故选D.
6.B
【详解】本题考查的是由三视图判断几何体
该图形的正视图为三角形,俯视图为圆形,则该图形是一个圆锥体,根据圆锥的体积公式即可求得结果.
易得该几何体为圆锥,圆的直径为8cm,高9cm,则,故选B.
7.B
【分析】中心投影下的三角板与投影三角板一定是相似的,再根据相似三角形对应边的比等于相似比,列式进行计算即可.
【详解】解:三角板的一边长为,则设投影三角板的对应边长为,
三角板与其投影的相似比为,
,
,
投影三角板的对应边长为.
故选:B.
【点睛】此题主要考查了中心投影与相似三角形的性质,熟练掌握中心投影的概念与相似三角形的性质是解答此题的关键.
8.C
【分析】根据影子的位置,再结合阳光的方向进行判断即可.
【详解】解:中午放学时太阳光线由东向西,
所以可判断小明当时的行驶方向是由北向南.
故选:C.
【点睛】本题考查了方位角和投影;结合阳光方向和影子方向确定行驶方向是解决问题的关键.
9.D
【详解】盲区就是看不到的地区,观察图形可解决.
解:根据盲区的定义,位于D的视点的盲区应该是三角形ABE的区域.
故选D.
10.C
【详解】试题分析:这个几何体零件的俯视图是一个正中间有一个小正方形的矩形,
所以它的俯视图是选项C中的图形.
故选C.
考点:简单组合体的三视图.
11.C
【分析】根据常见几何体的主视图,依次判断即可.
【详解】A.该三棱锥的主视图为中间有条线段的三角形,故不符合题意;
B.该圆锥的主视图为三角形,故不符合题意;
C.该圆柱的主视图为矩形,故符合题意;
D.该圆台的主视图为梯形,故不符合题意;
故选:C.
【点睛】本题考查常见几何体的三视图,掌握常见几何体的三视图是解答本题的关键.
12.C
【分析】圆锥的左视图就是从圆锥的左边看即可得到答案.
【详解】解:从圆锥的左边看可以看到一个等腰三角形.
故选C.
【点睛】本题考查了简单几何体的三视图,左视图是从几何体的左边看所得到的图形.
13.
【分析】根据几何体的三视图,得出该几何体为圆柱体,其底面直径为8,高为6,从而求出圆柱体体积.
【详解】解:由三视图可得,该几何体是一个底面直径为8,高为6的圆柱体,
∴该几何体的体积为:
故答案为:
【点睛】本题考查了利用三视图求空间几何体的体积的应用问题,是基础题目.
14.1
【详解】解:设王鹏的影长为xm,因为同一时刻在阳光下的物体的高与影长成比例,所以所以x=1
故答案为:1.
【点睛】本题考查成比例线段,正确列出比例式是解题关键.
15.60
【分析】本题考查平行投影,熟练掌握平行投影是解题的关键.设这栋楼的高度为,根据题意可列出关于x的方程,求解即可.
【详解】解:设这栋楼的高度为,
根据题意有:,
解得:,
故这栋楼的高度为.
故答案为:.
16.中心投影
【详解】考点:中心投影.
分析:皮影戏是有灯光照射下在影布上形成的投影,故是中心投影.
解答:解:皮影戏是有灯光照射下在影布上形成的投影,故是中心投影.
点评:本题属于基础题,考查了投影的知识,可运用投影的知识或直接联系生活实际解答.
17.24π
【分析】根据主视图确定圆柱的高为6,根据俯视图确定圆的直径为4即半径为2,利用公式计算即可.
【详解】∵
∴圆柱的高为6,圆的直径为4即半径为2,
∴圆柱的体积为==24π,
故答案为:24π.
【点睛】本题考查了圆柱的三视图,圆柱的体积,熟练读懂三视图,确定圆柱的高和直径是解题的关键.
18.该几何体是实心圆台.
【分析】根据此几何体的俯视图是圆环,主视图和左视图均是等腰梯形可知该几何体为实心圆台,然后作出图形即可.
【详解】∵此几何体的俯视图是圆环,主视图和左视图均是等腰梯形,∴该几何体是实心圆台,∴其形状为:实心圆台.
【点睛】本题考查了由三视图判断几何体的知识,由几何体的俯视图可确定该几何体的主视图和左视图,要熟练掌握.
19.见解析
【分析】主视图和左视图都是等腰梯形,俯视图是圆环,依此画出即可;
【详解】如图所示.
依次为主视图、左视图、俯视图
【点睛】考查了作图-三视图,主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.
20.(1)见解析
(2)米
【分析】(1)连接并延长交于点P,连接并延长交于F,点P和即为所求;
(2)先求出米,证明,得到,即,则米.
【详解】(1)解:如图所示,点P和即为所求;
(2)解:∵米,米,
∴米,
∵,,即,
∴,
∴,即,
∴米,
∴路灯灯泡距地面的高度为米.
【点睛】本题主要考查了相似三角形的应用举例,熟知相似三角形的性质与判定条件是解题的关键.
21.见解析
【详解】如图,
22.组成这个几何体的小正方体的个数是8个或9个或10个.
【分析】根据三视图,可知该几何体共有两列三行组成,底面有5个正方体,第二层最少有2个最多有4个正方体,第三层有1个,相加即可求解.
【详解】该几何体共有两列三行组成,底面有5个正方体,第二层有最少2个最多4个,第三层有1个,
5+2+1=8(个),
5+4+1=10(个).
答:组成这个几何体的小正方体的个数是8个或9个或10个.
【点睛】本题考查由三视图判断几何体,根据题目中要求的可能有多少个小正方体搭建这个几何体,根据“俯视图打地基,正视图疯狂盖,左视图拆违章”很容易就知道小正方体的个数,一定要将所有可能性考虑全面.
23.见解析
【分析】本题主要考查从不同方向看几何体.根据题意可得,从正面看有3列,每列小正方数形数目分别为3,1,4;从左面看有3列,每列小正方形数目分别为2,4,3.据此可画出图形,即可.
【详解】解:如图所示:
24.(1)见解析
(2) 4
【分析】(1)由已知条件可知,左视图有3列,每列小正方形数目分别为3,2,1;俯视图有3列,每列小正方数形数目分别为3,2,1,据此可画出图形.
(2)可在最底层第二列第三行加一个,第三列第二行加2个,第三列第三行加1个,共4个.
【详解】(1)画图如下:
(2)最多可再添加4个小正方体.
在第2层的第2行第2列和第3行第2列各添加1个小立方块,第3层的第3行第2列和第3行第3列各添加1个小立方块,这个几何体的俯视图和左视图不变,,故最多可再添加4个小立方块.
【点睛】本题考查三视图的画法,以及根据三视图求立方体个数,属于中等难度题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
