第七章空间图形的初步认识同步练习(含解析)
文档属性
| 名称 | 第七章空间图形的初步认识同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 848.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 10:05:18 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七章空间图形的初步认识
学校:___________姓名:___________班级:___________考号:___________
一、单选题
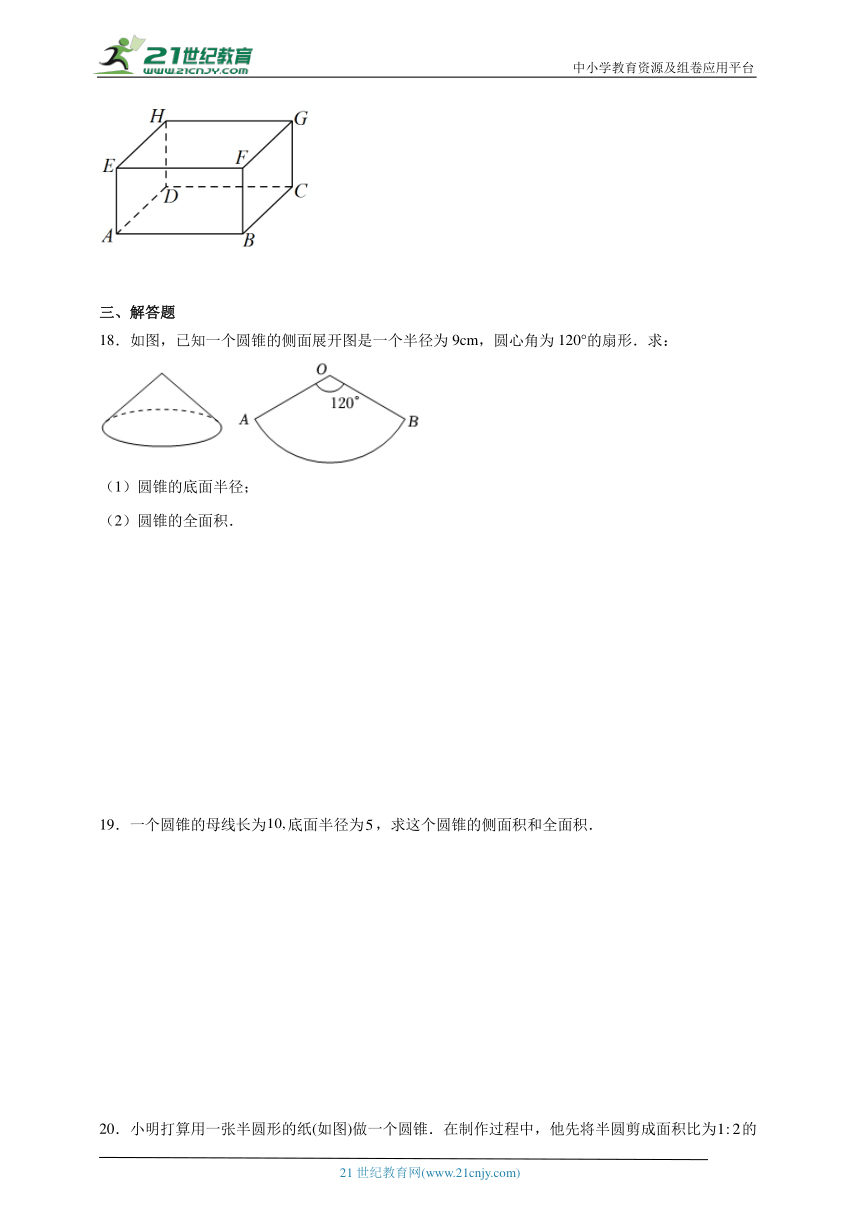
1.扇形的半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,则圆锥底面半径为( )
A.10cm B.20cm C.10πcm D.20πcm
2.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是cm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
3.下列图形经过折叠能围成柱体的是( )
A.①② B.①③ C.③④ D.②④
4.如图,圆柱体的表面展开后得到的平面图形是( )
A. B. C. D.
5.下列说法正确的是( )
A.长方体的截面形状一定是长方形; B.棱柱侧面的形状可能是一个三角形;
C.“天空划过一道流星”能说明“点动成线”; D.圆柱的截面一定是长方形.
6.已知圆锥的底面半径为,母线长为,则这个圆锥的侧面积为( )
A. B. C. D.
7.物理实验室有高度同为10cm的圆柱形容器A和B(如图),它们的底面半径分别为2cm和4cm,用一水龙头单独向A注水,3分钟后可以注满容器.在实验室课上,某同学将两容器在它们高度的一半用一个细水管连通(连接细管的容积忽略不计),仍用该水龙头向A注水,问6分钟后容器A中水的高度是( )cm.(注:若圆柱体底面半径为r,高为h,体积为V,则)
A.6 B.5 C.4 D.3
8.如图中柱体的个数是( )
A.3 B.4 C.5 D.6
9.如图所示,用经过A、B、C三点的平面截去正方体的一角,变成一个新的多面体,这个多面体的面数是
A.8 B.7 C.6 D.5
10.长方形的长为厘米,宽为厘米,若绕着它的宽旋转一周得到的圆柱的体积为( )立方厘米.
A. B. C. D.
11.如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距( )
A.0 B.1 C. D.
12.用一个半径为圆心角为的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A. B. C. D.
二、填空题
13.观察下图中的几何体,在横线上依次写出它们的名称.
14.下列说法中,①面数较多的立体图形就是多面体;②长方体是四棱柱,四棱柱是长方体;③长方形绕其一边旋转一周得到的立体图形是圆柱体;④棱锥底面边数与侧棱数相等;⑤直角三角形绕其一边旋转一周得到的立体图形是圆锥;⑥棱柱的上、下底面是形状,大小相同的多边形;⑦圆锥和圆柱的底面都是圆;⑧由某一图形绕着一条直线旋转一周所得到的几何体,一定不是多面体;⑨将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球体;其中正确的序号是 .
15.某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“功”字所在面相对面上的汉字是
16.直角三角板绕它的一条直角边所在的直线旋转一周,形成了圆锥,这种现象说明了 .
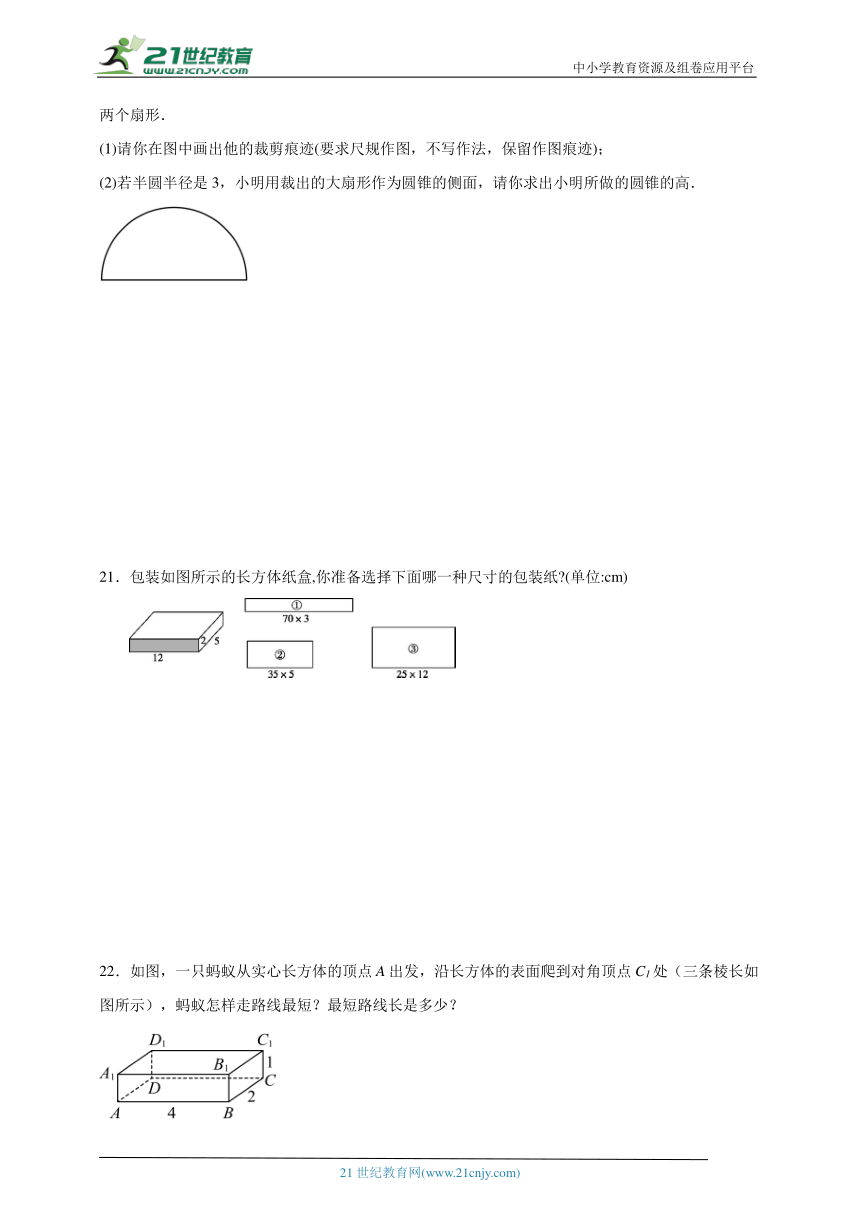
17.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
三、解答题
18.如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
19.一个圆锥的母线长为底面半径为,求这个圆锥的侧面积和全面积.
20.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
21.包装如图所示的长方体纸盒,你准备选择下面哪一种尺寸的包装纸 (单位:cm)
22.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),蚂蚁怎样走路线最短?最短路线长是多少?
23.如图,矩形中,,以上一点O为圆心,长为半径画恰与边相切,交于F点,连结,若将这个扇形围成一个圆锥,求这个圆锥的底面积S.
24.如图,若为等腰直角三角形,其中,,将等腰绕其斜边所在直线旋转一周,求所得几何体的全面积.
《第七章空间图形的初步认识》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B B C B B C B D
题号 11 12
答案 B B
1.A
【详解】试题解析:扇形的弧长为:=20πcm,
∴圆锥底面半径为20π÷2π=10cm,
故选A.
考点:圆锥的计算.
2.A
【详解】一只扇形的弧长是6πcm,则底面的半径即可求得,底面的半径,圆锥的高以及母线(扇形的半径)正好构成直角三角的三边,利用勾股定理即可求解:
设圆锥的底面半径是r,则2πr=6π,解得:r=3.
则圆锥的高是: (cm).故选A.
3.B
【分析】本题考查了棱柱的展开图根据展开图的特点逐项分析即可.
【详解】①③能围成棱柱,②,④围成棱柱时,有两个面重合,且少了个底面
故选B
4.B
【详解】圆柱体的侧面展开后得到的平面图形是矩形,上下两底是两个圆,故选B.
5.C
【分析】根据用平面截一个几何体,从不同的位置截取,得到的截面形状不一定相同,通过分析如何做截面即可得到答案.
【详解】解:A. 长方体的截面形状也可能是三角形,故该选项不正确,不符合题意;
B. 棱柱侧面的形状是平行四边形,不可能是三角形,故该选项不正确,不符合题意;
C. “天空划过一道流星”能说明“点动成线”,故该选项正确,符合题意;
D. 圆柱的截面不一定是长方形,也可能圆形,故该选项不正确,不符合题意;.
故选:C.
【点睛】本题考查了平面截一个几何体,点、线、面之间的关系,掌握好空间想象能力是解决本题的关键.
6.B
【分析】本题考查圆锥的侧面积,解题的关键是掌握圆锥的侧面积公式,进行解答,即可.
【详解】∵圆锥的底面半径为,母线长为,
∴圆锥的侧面积为:,
故选:B.
7.B
【分析】3分钟后可以注满容器A,可以算出水的流速,从而可以得出6分钟内水龙头的出水量,然后得出答案.
【详解】解:3分钟后可以注满容器A,A容器的体积为.
则6分钟的注入水量为,
设6分钟后容器A中水的高度是,
当时,,注入水量.
当时,,注入水量.
当时,,注入水量
故选:B.
【点睛】本题考查了认识立体图形,解题关键是要读懂题目的意思,也考查了同学们的物理知识和分类讨论的思想.
8.C
【分析】本题主要考查了柱体的识别,一个多面体有两个面互相平行且全等,余下的每个相邻两个面的交线互相平行,这样的多面体就为柱体,柱体分为圆柱和棱柱,据此进行判断即可.
【详解】解:柱体有①③④⑤⑥,共5个,
故选:C.
9.B
【分析】截去正方体一角变成一个多面体,这个多面体多了一个面,棱数不变,少了一个顶点.
【详解】解:由图可得,多面体的面数是7.
故选B.
【点睛】本题考查了正方体的截面,关键是明确正方体的面数,顶点数,棱的条数,形数结合,求出截去一个角后得到的几何体的面数,顶点数,棱的条数.
10.D
【分析】此题考查点、线、面、体问题,将长为厘米,宽为厘米的长方形绕它的一边旋转一周可得到两个不同的圆柱底面半径是厘米、高是厘米,要求它们的体积,可利用圆柱的体积公式列式解答即可,解题的关键是正确理解以长方形的长或宽为轴旋转一周得到的是两个不同的圆柱体.
【详解】解:由题意得,(立方厘米),
故选:.
11.B
【分析】如解图所示,经过折叠围成一个正方体后,点B与点C重合,从而得出结论.
【详解】解:如图所示,经过折叠围成一个正方体后,点B与点C重合,
∵AC=1
∴点A、B在围成的正方体上相距1
故选B.
【点睛】此题考查的是由展开图折成几何体,判断出围成一个正方体后,点B与点C重合是解题关键.
12.B
【分析】把扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
【详解】解:设此圆锥的底面半径为R,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
,
解得:
故选:B
【点睛】主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
13. 球 六棱柱 圆锥 三棱柱 圆柱 四棱锥
【分析】根据几何体的特征,逐一写出对应的几何体的名称即可.
【详解】解:第一幅图为:球;第二幅图为:六棱柱;第三幅图为:圆锥;第四幅图为:三棱柱;第五幅图为:圆柱;第六幅图为:四棱锥
故答案为:球,六棱柱,圆锥,三棱柱,圆柱,四棱锥.
【点睛】本题主要考查了几何体的认识,解题的关键在于能够熟练掌握几何体的特征.
14.③④⑥⑦⑧⑨
【分析】根据多面体的特征、棱柱的特征、圆锥的特征、面动成体等知识逐一判断即得答案.
【详解】解:①面数较多的立体图形不一定是多面体,如圆柱,故①说法错误;
②长方体是四棱柱,但四棱柱不一定是长方体,故②说法错误;
③长方形绕其一边旋转一周得到的立体图形是圆柱体,故③说法正确;
④棱锥底面边数与侧棱数相等,故④说法正确;
⑤直角三角形绕一直角边旋转一周得到的立体图形是圆锥,绕斜边旋转一周得到的立体图形是两个圆锥的组合体,故⑤说法错误;
⑥直棱柱的上、下底面是形状,大小相同的多边形,故⑥说法正确;
⑦圆锥和圆柱的底面都是圆,故⑦说法正确;
⑧由某一图形绕着一条直线旋转一周所得到的几何体,一定不是多面体,故⑧说法正确;
⑨将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球体,故⑨说法正确;
综上,正确的结论是:③④⑦⑧⑨;
故答案为:③④⑥⑦⑧⑨.
【点睛】本题考查了多面体、棱柱、圆锥和面动成体等知识,熟知常见立体图形的特点是解题的关键.
15.然
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,找对面的口诀是:“跳一跳,找对面,找不到,拐个弯.”根据这一特点作答即可.
【详解】由正方体展开图的性质,可得:
“成”与“非”是相对面,
“功”与“然”是相对面,
“绝”与“偶”是相对面.
故答案为:然.
【点睛】此题考查了正方体相对面上的字,解题的关键是掌握正方体展开图的性质.
16.面动成体
【分析】本题主要考查了点、线、面、体的关系,解题的关键在于熟练掌握点动成线,线动成面,面动成体.
根据点动成线,线动成面,面动成体进行解答即可.
【详解】解:直角三角板绕它的直角边旋转一周,形成了一个圆锥体,这说明了面动成体,
故答案为:面动成体.
17.
【分析】根据直线与平面垂直的定义进行判断即可.
【详解】解:∵面与面组成的图形看作直立于面上的合页型折纸,
∴棱面,
故答案为:.
【点睛】本题考查认识立体图形,理解直线垂直平面的定义是正确判断的前提.
18.(1)圆锥的底面半径为;(2)圆锥的全面积
【分析】(1)扇形的弧长公式l=,利用展开后扇形的弧长即为展开前圆锥底面圆的周长求出半径;
(2)S圆锥= S侧+S底,S侧面=,S底=,(R=扇形半径即圆锥母线长,r=底面圆半径)将已知条件代入即可.
【详解】解:(1)设圆锥的底面半径为.
扇形的弧长为,
∴,
解得,
∴圆锥的底面半径为.
(2)圆锥的侧面积:S侧面==.
园锥的底面积:S底=.
∴圆锥的全面积S全=S侧+S底=.
【点睛】本题考查圆锥相关的计算,要求掌握圆锥侧面积与底面积的计算公式,侧面展开图扇形相关的面积和弧长的求算,注意求圆锥面积时母线与底面圆半径的区分.
19.侧面积为,全面积为
【分析】根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则利用扇形的面积公式直接可计算出这个圆锥的侧面积,然后计算侧面积与底面积的和得到圆锥的全面积.
【详解】解:这个圆锥的侧面积
这个圆锥的全面积=50π+π×52=75π.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
20.(1)见解析
(2)
【分析】(1)先作直径的垂直平分线,找出圆心O,再以点B为圆心,以为半径画弧,交半圆于点C,由,可知,,根据半径相同的扇形,面积比等于圆心角的比,可知;
(2)首先求得大扇形的弧长,然后求得围成的圆锥的底面半径,最后利用勾股定理求得圆锥的高即可.
【详解】(1)解:如图所示,直线即为裁剪痕迹;
作图过程:先作出直径的垂直平分线,找到圆心O,再以点B为圆心,以为半径画弧,交半圆于点C,直线即为裁剪痕迹.
(2)解:半圆的半径为3,
半圆的弧长为,
剪成面积比为的两个扇形.
大扇形的弧长为,
设围成的圆锥的底面半径为r,则,
解得,
圆锥的高为.
【点睛】本题考查勾股定理,圆锥的计算及复杂作图,解题的关键是弄清扇形的相关量与圆锥的相关量之间的对应关系.圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
21.都不选择,理由见解析
【分析】根据长方体的侧面展开图的特征,把这个长方体的展开,然后与三种不同尺寸的纸进行比较即可.
【详解】解:
根据长方体的展开图可知:包装纸的长:2×2+5×2=14(厘米)
包装纸的宽:2×2+12=16(厘米),
所以三种包装纸都不符合要求.
【点睛】此题考查的目的是理解掌握长方体的特征,以及长方体的展开图的特点.
22.线路(1)最短,为5
【分析】此题主要考查了平面展开图最短路径问题,利用分类讨论得出是解题关键.
分别利用从不同的表面得出其路径长,进而得出答案.
【详解】解:有三种展开方式,
如图(1),,所以.
如图(2),.
如图(3),
因为,
所以,路线(1)最短,最短路线是5.
23.16πcm2
【分析】连接EO,可得扇形的半径12cm,利用相应的三角函数可求得扇形的圆心角,进而得出底面圆的半径,代入圆的面积公式即可.
【详解】解:连接EO,
∵恰与边相切,
∴EO⊥DC,
∴EO=BC=BO=FO=12cm,
AO=AB﹣OB=18﹣12=6cm,
∴Rt△OFA中,cos∠FOA==,
∴∠FOA=60°,∴∠FOB=120°,
∴弧BF长l=,
圆锥的底面圆周长2πr=,
∴r=4(cm).
∴S=πr2=16π(cm2).
.
【点睛】此题主要考查了圆锥的有关计算,解答此题需熟练圆锥侧面展开图与扇形关系,得出FO=EO=BO是解题关键.
24.
【分析】易得此几何体为圆锥,那么全面积底面周长母线长.
【详解】解:作,
由题意知,在中,,,
,
,
以为半径的圆的周长,
得到的几何体全面积为.
【点睛】此题主要考查了圆锥侧面积的计算,解题的关键是利用圆锥的侧面积底面周长母线长得出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七章空间图形的初步认识
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.扇形的半径为30cm,圆心角为120°,用它做成一个圆锥的侧面,则圆锥底面半径为( )
A.10cm B.20cm C.10πcm D.20πcm
2.小明用图中所示的扇形纸片作一个圆锥的侧面,已知扇形的半径为5cm,弧长是cm,那么这个的圆锥的高是( )
A.4cm B.6cm C.8cm D.2cm
3.下列图形经过折叠能围成柱体的是( )
A.①② B.①③ C.③④ D.②④
4.如图,圆柱体的表面展开后得到的平面图形是( )
A. B. C. D.
5.下列说法正确的是( )
A.长方体的截面形状一定是长方形; B.棱柱侧面的形状可能是一个三角形;
C.“天空划过一道流星”能说明“点动成线”; D.圆柱的截面一定是长方形.
6.已知圆锥的底面半径为,母线长为,则这个圆锥的侧面积为( )
A. B. C. D.
7.物理实验室有高度同为10cm的圆柱形容器A和B(如图),它们的底面半径分别为2cm和4cm,用一水龙头单独向A注水,3分钟后可以注满容器.在实验室课上,某同学将两容器在它们高度的一半用一个细水管连通(连接细管的容积忽略不计),仍用该水龙头向A注水,问6分钟后容器A中水的高度是( )cm.(注:若圆柱体底面半径为r,高为h,体积为V,则)
A.6 B.5 C.4 D.3
8.如图中柱体的个数是( )
A.3 B.4 C.5 D.6
9.如图所示,用经过A、B、C三点的平面截去正方体的一角,变成一个新的多面体,这个多面体的面数是
A.8 B.7 C.6 D.5
10.长方形的长为厘米,宽为厘米,若绕着它的宽旋转一周得到的圆柱的体积为( )立方厘米.
A. B. C. D.
11.如图是边长为1的六个小正方形组成的平面图形,经过折叠能围成一个正方体,那么点A、B在围成的正方体上相距( )
A.0 B.1 C. D.
12.用一个半径为圆心角为的扇形围成一个圆锥,则这个圆锥的底面半径是( )
A. B. C. D.
二、填空题
13.观察下图中的几何体,在横线上依次写出它们的名称.
14.下列说法中,①面数较多的立体图形就是多面体;②长方体是四棱柱,四棱柱是长方体;③长方形绕其一边旋转一周得到的立体图形是圆柱体;④棱锥底面边数与侧棱数相等;⑤直角三角形绕其一边旋转一周得到的立体图形是圆锥;⑥棱柱的上、下底面是形状,大小相同的多边形;⑦圆锥和圆柱的底面都是圆;⑧由某一图形绕着一条直线旋转一周所得到的几何体,一定不是多面体;⑨将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球体;其中正确的序号是 .
15.某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方体中,与“功”字所在面相对面上的汉字是
16.直角三角板绕它的一条直角边所在的直线旋转一周,形成了圆锥,这种现象说明了 .
17.如图,在长方体中,可以把面与面组成的图形看作直立于面上的合页型折纸,从而说明棱 ⊥面.
三、解答题
18.如图,已知一个圆锥的侧面展开图是一个半径为9cm,圆心角为120°的扇形.求:
(1)圆锥的底面半径;
(2)圆锥的全面积.
19.一个圆锥的母线长为底面半径为,求这个圆锥的侧面积和全面积.
20.小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为的两个扇形.
(1)请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);
(2)若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.
21.包装如图所示的长方体纸盒,你准备选择下面哪一种尺寸的包装纸 (单位:cm)
22.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),蚂蚁怎样走路线最短?最短路线长是多少?
23.如图,矩形中,,以上一点O为圆心,长为半径画恰与边相切,交于F点,连结,若将这个扇形围成一个圆锥,求这个圆锥的底面积S.
24.如图,若为等腰直角三角形,其中,,将等腰绕其斜边所在直线旋转一周,求所得几何体的全面积.
《第七章空间图形的初步认识》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B B C B B C B D
题号 11 12
答案 B B
1.A
【详解】试题解析:扇形的弧长为:=20πcm,
∴圆锥底面半径为20π÷2π=10cm,
故选A.
考点:圆锥的计算.
2.A
【详解】一只扇形的弧长是6πcm,则底面的半径即可求得,底面的半径,圆锥的高以及母线(扇形的半径)正好构成直角三角的三边,利用勾股定理即可求解:
设圆锥的底面半径是r,则2πr=6π,解得:r=3.
则圆锥的高是: (cm).故选A.
3.B
【分析】本题考查了棱柱的展开图根据展开图的特点逐项分析即可.
【详解】①③能围成棱柱,②,④围成棱柱时,有两个面重合,且少了个底面
故选B
4.B
【详解】圆柱体的侧面展开后得到的平面图形是矩形,上下两底是两个圆,故选B.
5.C
【分析】根据用平面截一个几何体,从不同的位置截取,得到的截面形状不一定相同,通过分析如何做截面即可得到答案.
【详解】解:A. 长方体的截面形状也可能是三角形,故该选项不正确,不符合题意;
B. 棱柱侧面的形状是平行四边形,不可能是三角形,故该选项不正确,不符合题意;
C. “天空划过一道流星”能说明“点动成线”,故该选项正确,符合题意;
D. 圆柱的截面不一定是长方形,也可能圆形,故该选项不正确,不符合题意;.
故选:C.
【点睛】本题考查了平面截一个几何体,点、线、面之间的关系,掌握好空间想象能力是解决本题的关键.
6.B
【分析】本题考查圆锥的侧面积,解题的关键是掌握圆锥的侧面积公式,进行解答,即可.
【详解】∵圆锥的底面半径为,母线长为,
∴圆锥的侧面积为:,
故选:B.
7.B
【分析】3分钟后可以注满容器A,可以算出水的流速,从而可以得出6分钟内水龙头的出水量,然后得出答案.
【详解】解:3分钟后可以注满容器A,A容器的体积为.
则6分钟的注入水量为,
设6分钟后容器A中水的高度是,
当时,,注入水量.
当时,,注入水量.
当时,,注入水量
故选:B.
【点睛】本题考查了认识立体图形,解题关键是要读懂题目的意思,也考查了同学们的物理知识和分类讨论的思想.
8.C
【分析】本题主要考查了柱体的识别,一个多面体有两个面互相平行且全等,余下的每个相邻两个面的交线互相平行,这样的多面体就为柱体,柱体分为圆柱和棱柱,据此进行判断即可.
【详解】解:柱体有①③④⑤⑥,共5个,
故选:C.
9.B
【分析】截去正方体一角变成一个多面体,这个多面体多了一个面,棱数不变,少了一个顶点.
【详解】解:由图可得,多面体的面数是7.
故选B.
【点睛】本题考查了正方体的截面,关键是明确正方体的面数,顶点数,棱的条数,形数结合,求出截去一个角后得到的几何体的面数,顶点数,棱的条数.
10.D
【分析】此题考查点、线、面、体问题,将长为厘米,宽为厘米的长方形绕它的一边旋转一周可得到两个不同的圆柱底面半径是厘米、高是厘米,要求它们的体积,可利用圆柱的体积公式列式解答即可,解题的关键是正确理解以长方形的长或宽为轴旋转一周得到的是两个不同的圆柱体.
【详解】解:由题意得,(立方厘米),
故选:.
11.B
【分析】如解图所示,经过折叠围成一个正方体后,点B与点C重合,从而得出结论.
【详解】解:如图所示,经过折叠围成一个正方体后,点B与点C重合,
∵AC=1
∴点A、B在围成的正方体上相距1
故选B.
【点睛】此题考查的是由展开图折成几何体,判断出围成一个正方体后,点B与点C重合是解题关键.
12.B
【分析】把扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
【详解】解:设此圆锥的底面半径为R,
根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得,
,
解得:
故选:B
【点睛】主要考查了圆锥侧面展开扇形与底面圆之间的关系,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把的扇形的弧长等于圆锥底面周长作为相等关系,列方程求解.
13. 球 六棱柱 圆锥 三棱柱 圆柱 四棱锥
【分析】根据几何体的特征,逐一写出对应的几何体的名称即可.
【详解】解:第一幅图为:球;第二幅图为:六棱柱;第三幅图为:圆锥;第四幅图为:三棱柱;第五幅图为:圆柱;第六幅图为:四棱锥
故答案为:球,六棱柱,圆锥,三棱柱,圆柱,四棱锥.
【点睛】本题主要考查了几何体的认识,解题的关键在于能够熟练掌握几何体的特征.
14.③④⑥⑦⑧⑨
【分析】根据多面体的特征、棱柱的特征、圆锥的特征、面动成体等知识逐一判断即得答案.
【详解】解:①面数较多的立体图形不一定是多面体,如圆柱,故①说法错误;
②长方体是四棱柱,但四棱柱不一定是长方体,故②说法错误;
③长方形绕其一边旋转一周得到的立体图形是圆柱体,故③说法正确;
④棱锥底面边数与侧棱数相等,故④说法正确;
⑤直角三角形绕一直角边旋转一周得到的立体图形是圆锥,绕斜边旋转一周得到的立体图形是两个圆锥的组合体,故⑤说法错误;
⑥直棱柱的上、下底面是形状,大小相同的多边形,故⑥说法正确;
⑦圆锥和圆柱的底面都是圆,故⑦说法正确;
⑧由某一图形绕着一条直线旋转一周所得到的几何体,一定不是多面体,故⑧说法正确;
⑨将一个半圆绕它的直径所在的直线旋转一周得到的几何体是球体,故⑨说法正确;
综上,正确的结论是:③④⑦⑧⑨;
故答案为:③④⑥⑦⑧⑨.
【点睛】本题考查了多面体、棱柱、圆锥和面动成体等知识,熟知常见立体图形的特点是解题的关键.
15.然
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,找对面的口诀是:“跳一跳,找对面,找不到,拐个弯.”根据这一特点作答即可.
【详解】由正方体展开图的性质,可得:
“成”与“非”是相对面,
“功”与“然”是相对面,
“绝”与“偶”是相对面.
故答案为:然.
【点睛】此题考查了正方体相对面上的字,解题的关键是掌握正方体展开图的性质.
16.面动成体
【分析】本题主要考查了点、线、面、体的关系,解题的关键在于熟练掌握点动成线,线动成面,面动成体.
根据点动成线,线动成面,面动成体进行解答即可.
【详解】解:直角三角板绕它的直角边旋转一周,形成了一个圆锥体,这说明了面动成体,
故答案为:面动成体.
17.
【分析】根据直线与平面垂直的定义进行判断即可.
【详解】解:∵面与面组成的图形看作直立于面上的合页型折纸,
∴棱面,
故答案为:.
【点睛】本题考查认识立体图形,理解直线垂直平面的定义是正确判断的前提.
18.(1)圆锥的底面半径为;(2)圆锥的全面积
【分析】(1)扇形的弧长公式l=,利用展开后扇形的弧长即为展开前圆锥底面圆的周长求出半径;
(2)S圆锥= S侧+S底,S侧面=,S底=,(R=扇形半径即圆锥母线长,r=底面圆半径)将已知条件代入即可.
【详解】解:(1)设圆锥的底面半径为.
扇形的弧长为,
∴,
解得,
∴圆锥的底面半径为.
(2)圆锥的侧面积:S侧面==.
园锥的底面积:S底=.
∴圆锥的全面积S全=S侧+S底=.
【点睛】本题考查圆锥相关的计算,要求掌握圆锥侧面积与底面积的计算公式,侧面展开图扇形相关的面积和弧长的求算,注意求圆锥面积时母线与底面圆半径的区分.
19.侧面积为,全面积为
【分析】根据圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,则利用扇形的面积公式直接可计算出这个圆锥的侧面积,然后计算侧面积与底面积的和得到圆锥的全面积.
【详解】解:这个圆锥的侧面积
这个圆锥的全面积=50π+π×52=75π.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
20.(1)见解析
(2)
【分析】(1)先作直径的垂直平分线,找出圆心O,再以点B为圆心,以为半径画弧,交半圆于点C,由,可知,,根据半径相同的扇形,面积比等于圆心角的比,可知;
(2)首先求得大扇形的弧长,然后求得围成的圆锥的底面半径,最后利用勾股定理求得圆锥的高即可.
【详解】(1)解:如图所示,直线即为裁剪痕迹;
作图过程:先作出直径的垂直平分线,找到圆心O,再以点B为圆心,以为半径画弧,交半圆于点C,直线即为裁剪痕迹.
(2)解:半圆的半径为3,
半圆的弧长为,
剪成面积比为的两个扇形.
大扇形的弧长为,
设围成的圆锥的底面半径为r,则,
解得,
圆锥的高为.
【点睛】本题考查勾股定理,圆锥的计算及复杂作图,解题的关键是弄清扇形的相关量与圆锥的相关量之间的对应关系.圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
21.都不选择,理由见解析
【分析】根据长方体的侧面展开图的特征,把这个长方体的展开,然后与三种不同尺寸的纸进行比较即可.
【详解】解:
根据长方体的展开图可知:包装纸的长:2×2+5×2=14(厘米)
包装纸的宽:2×2+12=16(厘米),
所以三种包装纸都不符合要求.
【点睛】此题考查的目的是理解掌握长方体的特征,以及长方体的展开图的特点.
22.线路(1)最短,为5
【分析】此题主要考查了平面展开图最短路径问题,利用分类讨论得出是解题关键.
分别利用从不同的表面得出其路径长,进而得出答案.
【详解】解:有三种展开方式,
如图(1),,所以.
如图(2),.
如图(3),
因为,
所以,路线(1)最短,最短路线是5.
23.16πcm2
【分析】连接EO,可得扇形的半径12cm,利用相应的三角函数可求得扇形的圆心角,进而得出底面圆的半径,代入圆的面积公式即可.
【详解】解:连接EO,
∵恰与边相切,
∴EO⊥DC,
∴EO=BC=BO=FO=12cm,
AO=AB﹣OB=18﹣12=6cm,
∴Rt△OFA中,cos∠FOA==,
∴∠FOA=60°,∴∠FOB=120°,
∴弧BF长l=,
圆锥的底面圆周长2πr=,
∴r=4(cm).
∴S=πr2=16π(cm2).
.
【点睛】此题主要考查了圆锥的有关计算,解答此题需熟练圆锥侧面展开图与扇形关系,得出FO=EO=BO是解题关键.
24.
【分析】易得此几何体为圆锥,那么全面积底面周长母线长.
【详解】解:作,
由题意知,在中,,,
,
,
以为半径的圆的周长,
得到的几何体全面积为.
【点睛】此题主要考查了圆锥侧面积的计算,解题的关键是利用圆锥的侧面积底面周长母线长得出.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
