5.7二次函数的应用同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
5.7二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度时,.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
2.如图,直线与两坐标轴交于A,B两点,点P是线段AB上一动点(不与A,B两端点重合),过点P作PC⊥x轴于点C,作PD⊥y轴于点D,小明认为矩形PCOD的周长不变且始终为6;小红认为矩形PCOD的面积有最大值,最大值为3.关于小明与小红的判断,下面说法正确的是( )
A.小明与小红都是正确的 B.小明与小红都是错误的
C.小明是正确的,小红是错误的 D.小明是错误的,小红是正确的
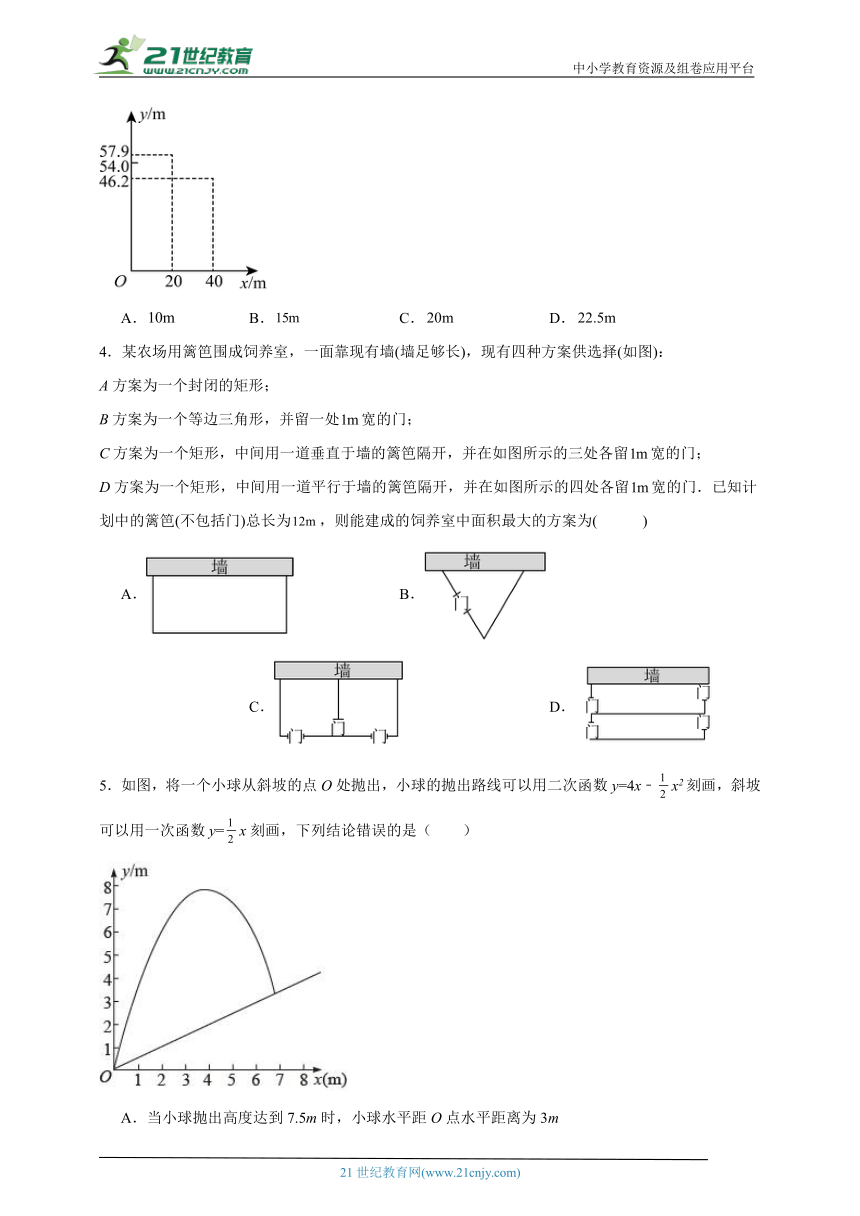
3.跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度(单位:)与水平距离(单位:)近似满足函数关系().下图记录了某运动员起跳后的与的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为
A. B. C. D.
4.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留宽的门.已知计划中的篱笆(不包括门)总长为,则能建成的饲养室中面积最大的方案为( )
A. B. C. D.
5.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.斜坡的坡度为1:2
6.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量增加),那么等于( )
A. B. C. D.
7.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
8.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1 B.2 C.3 D.4
9.如图,在Rt△ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,则S关于t的函数图象大致为( )
A. B.
C. D.
10.如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )
A. B. C. D.
11.太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻在一定条件下,直杆的太阳影子长度单位:米与时刻单位:时的关系满足函数关系是常数,如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是()
A. B.13 C. D.
12.如图,抛物线交x轴的负半轴于点A,点B是y轴的正半轴上一点,点A关于点B的对称点A 恰好落在抛物线上.过点A 作x轴的平行线交抛物线于另一点C,则点A 的纵坐标为()
A.1.5 B.2 C.2.5 D.3
二、填空题
13.为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为 元时,可使每天所获销售利润最大.
14.某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为 .
15.如图,在平面直角坐标系中,点A(4,8)在抛物线上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
16.为了让农民能种植高产、易发芽的种子,某农科实验基地大力开展种子实验.该实验基地两年前有100种种子,经过两年不断地努力,现在已有144种种子.若培育的种子平均每年的增长率为x,则x的值为 .
17.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
三、解答题
18.如图,已知抛物线的对称轴为直线,且抛物线与轴交于、两点,与轴交于点,其中,.
(1)若直线经过、两点,求直线和抛物线的解析式;
(2)在抛物线的对称轴上找一点,使点到点的距离与到点的距离之和最小,求出点的坐标;
(3)设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标.
19.如图,在直角坐标系xOy中有一梯形ABCO,顶点C在x正半轴上,A、B两点在第一象限;且AB∥CO,AO=BC=2,AB=3,OC=5.点P在x轴上,从点(﹣2,0)出发,以每秒1个单位长度的速度沿x轴向正方向运动;同时,过点P作直线l,使直线l和x轴向正方向夹角为30°.设点P运动了t秒,直线l扫过梯形ABCO的面积为S扫.
(1)求A、B两点的坐标;
(2)当t=2秒时,求S扫的值;
(3)求S扫与t的函数关系式,并求出直线l扫过梯形ABCO面积的时点P的坐标.
20.已知抛物线与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
21.某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数表达式为
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数表达式;
(2)当该产品的售价为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
22.已知函数均为一次函数,m为常数.
(1)如图1,将直线绕点逆时针旋转45°得到直线,直线交y轴于点B.若直线恰好是中某个函数的图象,请直接写出点B坐标以及m可能的值;
(2)若存在实数b,使得成立,求函数图象间的距离;
(3)当时,函数图象分别交x轴,y轴于C,E两点,图象交x轴于D点,将函数的图象最低点F向上平移个单位后刚好落在一次函数图象上,设的图象,线段,线段围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
23.如图,抛物线与x轴交于点A(﹣, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
24.已知y是关于x的函数,若其函数图象经过点P(t,t),则称点P为函数图象上的“和谐点”.
(1)求出直线y=3x﹣2的“和谐点”坐标;
(2)若抛物线y=﹣x2+(a+1)x﹣a+1上有“和谐点”,且“和谐点”为A(x1,y1)和B(x2,y2),求W=x12+x22的最小值;
(3)若函数y=x2+(m﹣t+1)x+n+t﹣2的图象上存在唯一的一个“和谐点”且当2≤m≤3时,n的最小值为t,求t的值.
《5.7二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C A C C C C C
题号 11 12
答案 C B
1.D
【分析】根据函数的图象中的信息判断即可.
【详解】①由图象知小球在空中达到的最大高度是;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:,
把代入得,解得,
∴函数解析式为,
把代入解析式得,,
解得:或,
∴小球的高度时,或,故④错误;
故选D.
【点睛】本题考查了二次函数的应用,解此题的关键是正确的理解题意
2.C
【分析】设P(x,)().根据周长公式求出周长,即可判定小明的正误;根据面积公式求出面积,结合二次函数的性质,即可判断小红的正误.
【详解】设P(x,)(),
∵,
∴周长不变,且始终为6,即小明正确;
∵,
∴当时,最大,最大为,即小红是错误的.
故选C
【点睛】本题考查一次函数与二次函数的综合.掌握二次函数的性质是解题关键.
3.B
【详解】分析: 根据抛物线的对称性即可判断出对称轴的范围.
详解:设对称轴为,
由(,)和(,)可知,,
由(,)和(,)可知,,
∴,
故选B.
点睛:考查抛物线的对称性,熟练运用抛物线的对称性质是解题的关键.
4.C
【分析】设建成的饲养室的面积为,先根据篱笆总长、矩形与等边三角形的面积公式求出的函数关系式,再利用二次函数的性质求最值,然后比较大小即可得.
【详解】设建成的饲养室的面积为,
对于A选项,如图(1),设边的长为,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为18;
对于B选项,如图(2),设,则,解得,
由等边三角形的性质得:AB边上的高为,
则;
对于C选项,如图(3),设,则,,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为;
对于D选项,如图(4),设,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为16;
因为,
所以建成的饲养室中面积最大的方案是C方案,
故选:C.
【点睛】本题考查了二次函数的应用、矩形与等边三角形的面积公式,依据题意,分别求出各图形的面积的函数表达式是解题关键.
5.A
【分析】求出当y=7.5时,x的值,判定选项A;根据二次函数的性质求出对称轴,根据二次函数性质判断选项B;求出抛物线与直线的交点,判断选项C,根据直线解析式和坡度的定义判断选项D.
【详解】当y=7.5时,7.5=4x﹣x2,
整理得x2﹣8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5cm,选项A错误,符合题意;
y=4x﹣x2
=﹣(x﹣4)2+8,
则抛物线的对称轴为x=4,
∴当x>4时,y随x的增大而减小,即小球距O点水平距离超过4米呈下降趋势,选项B正确,不符合题意;
,
解得,,,
则小球落地点距O点水平距离为7米,选项C正确,不符合题意;
∵斜坡可以用一次函数y=x刻画,
∴斜坡的坡度为1:2,选项D正确,不符合题意;
故选A.
【点睛】本题考查的是解直角三角形的——坡度问题、二次函数的性质,掌握坡度的概念、二次函数的性质是解题的关键.
6.C
【分析】第档次产品比最低档次产品提高了个档次,则数量在60的基础上减少了,每件产品利润在8的基础上增加,据此可求出总利润关系,求出最值即可.
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
【点睛】本题考查了二次函数的实际应用,借助二次函数解决实际问题是本题的关键.
7.C
【分析】根据题中已知条件求出函数h=at2+bt的对称轴t=4,在t=4s时,小球的高度最高.
【详解】解:由题意可知:小球发射后第2秒与第6秒时的高度相等,
即4a+2b=36a+6b,
解得b=﹣8a,
函数h=at2+bt的对称轴t=﹣=4,
故在t=4s时,小球的高度最高,
故选:C.
【点睛】本题主要考查了二次函数的实际应用,求出抛物线对称轴是解题关键.
8.C
【分析】根据等量关系“四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积”列出函数关系求最小值.
【详解】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ
= ×12×6- (6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故选C.
【点睛】本题考查了函数关系式的求法以及最值的求法,解题的关键是根据题意列出函数关系式,并根据二次函数的性质求出最值.
9.C
【分析】根据已知条件得到△ABC是等腰直角三角形,推出四边形EFCD是正方形,设正方形的边长为a,当移动的距离a时,如图2,,根据函数关系式即可得到结论.
【详解】解:∵在直角三角形ABC中,∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵EF⊥BC,ED⊥AC,
∴四边形EFCD是矩形,
∵E是AB的中点,
∴EF=AC,DE=BC,
∴EF=ED,
∴四边形EFCD是正方形,
设正方形的边长为a,如图1,当移动的距离当移动的距离>a 时,如图2,,
∴S关于t的函数图象大致为C选项,故选:C.
【点睛】本题考查动点问题的函数图象,正方形的性质、勾股定理等知识,解题的关键是读懂题意,学会分类讨论的思想,属于中考常考题型.
10.C
【详解】试题分析:解决本题的关键是正确确定y与x之间的函数解析式.
解:∵运动时间x(s),则CP=x,CO=2x;
∴S△CPO=CP CO=x 2x=x2.
∴则△CPO的面积y(cm2)与运动时间x(s)之间的函数关系式是:y=x2(0≤x≤3),
故选C.
考点:动点问题的函数图象;二次函数的图象.
11.C
【详解】把(12,0.6)、(13,0.35)、(14,0.4)代入l=at2+bt+c中得:
,解得,
∴l=0.15t2-4t+27,
∵0.15>0,
∴l有最小值,
当t=-=≈13.33时,该地影子最短;
故选C.
【点睛】错因分析 中等题.失分原因:没有理解本题考查的真正意图,通过二次函数图象上的点结合函数性质,推断对称轴位置.
12.B
【分析】先求出点A坐标,利用对称可得点横坐标,代入可得纵坐标.
【详解】解:令得,即
解得
点B是y轴的正半轴上一点,点A关于点B的对称点A 恰好落在抛物线上
点的横坐标为1
当时,
所以点A 的纵坐标为2.
故选:B
【点睛】本题考查了二次函数的图像,熟练利用函数解析式求点的坐标是解题的关键.
13.80
【分析】根据每天获得利润=单件利润×销售量列出二次函数即可求解.
【详解】解:设销售单价降低x元时,则销售单价是(100-x)元时,每天获利y元.
根据题意,得
y=(100-50-x)(50+5x)
=-5x2+200x+2500
=-5(x-20)2+4500
∵-5<0,当x=20时,y有最大值,
即100-x=80,80>50,
答:当销售单价是80元时,每天获利最多.
故答案为80.
【点睛】本题考查了二次函数的应用,解决本题的关键是掌握销售问题的数量关系.
14.或
【分析】根据平均增长问题,可得答案.
【详解】解:y与x之间的关系应表示为y=2(x+1)2.
故答案为:y=2(x+1)2.
【点睛】本题考查了函数关系式,利用增长问题获得函数解析式是解题关键,注意增加x倍是原来的(x+1)倍.
15.
【分析】利用待定系数法求出函数解析式,然后设点C横坐标为m,则CD=CE=2m,从而得出点E坐标为(m,8 2m),将点E坐标代入解析式求出m即可解决问题.
【详解】解:把A(4,8)代入中得8=16a,
解得a=,
∴,
设点C横坐标为m,则CD=CE=2m,
∴点E坐标为(m,8﹣2m),
∴=8﹣2m,
解得m=(舍)或m=,
∴CD=2m=,
故答案为:.
【点睛】本题考查二次函数的应用,待定系数法,解题关键是设出点C横坐标,表示出点E的坐标.
16.20%
【分析】利用该实验基地现在拥有的种子种数=该实验基地两年前拥有的种子种数×(1+培育的种子平均每年的增长率)2,可得出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:根据题意得:,
解得:(不符合题意,舍去),
∴x的值为.
故答案为:.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
17.80
【分析】直接利用每件利润×销量=总利润,进而得出每天盈利与x的关系式,配方即可得出答案.
【详解】解:设当销售单价为x元时,每天盈利为y元,
则y=(x-50)[100-2(x-60)]
=-2x2+320x-11000
=-2(x-80)2+1800,
∵-2<0,
∴当x=80时,y有最大值,且为1800,
答:当销售单价为80元时,每天获取的利润最大,最大利润是1800元.
【点睛】此题主要考查了二次函数的应用,正确得出函数关系式是解题关键.
18.(1)抛物线的解析式为,直线的解析式为.(2);(3)的坐标为或或或.
【详解】分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
详解:(1)依题意得:,解得:,
∴抛物线的解析式为.
∵对称轴为,且抛物线经过,
∴把、分别代入直线,
得,解之得:,
∴直线的解析式为.
(2)直线与对称轴的交点为,则此时的值最小,把代入直线得,
∴.即当点到点的距离与到点的距离之和最小时的坐标为.
(注:本题只求坐标没说要求证明为何此时的值最小,所以答案未证明的值最小的原因).
(3)设,又,,
∴,,,
①若点为直角顶点,则,即:解得:,
②若点为直角顶点,则,即:解得:,
③若点为直角顶点,则,即:解得:
,.
综上所述的坐标为或或或.
点睛:本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式、利用轴对称性质确定线段的最小长度、难度不是很大,是一道不错的中考压轴题.
19.(1)(1,),(4,);(2);(3);P的坐标为(5﹣2,0).
【分析】(1)两底的差的一半就是A的横坐标;过A、B作x轴的垂线,在构建的直角三角形中根据OA的长及两底的差便可求出梯形的高即A点的纵坐标.得出A点坐标后向右平移3个单位就是B点的坐标.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,由此可求出△ADO的面积及直线l扫过的面积.
(3)本题要分三种情况进行讨论:
①当P在原点左侧,即当0≤t<2时,重合部分是个三角形,如果设直线l与AO,AB分别交于E,F,可根据△AEF∽△AOD,用相似比求出其面积.即可得出S,t的函数关系式.
②当P在O点右侧(包括和O重合),而F点在B点左侧时,即当2≤t<3时,扫过部分是个梯形,可根据梯形的面积计算方法即可得出直线l扫过部分的面积.也就能得出S,t的函数关系式.
③当P点在C点左侧(包括和C点重合),F点在B点右侧(包括和B点重合),即当3≤t≤7时,扫过部分是个五边形,可用梯形ABCO的面积减去△MPC的面积来得出S,t的函数关系式.
【详解】(1)过A作AD⊥OC于D,过B作BE⊥OC于E,则ADEB是矩形.
∵ADEB是矩形,∴AD=BE=3.
∵AO=BC,∴△AOD≌△BCE,∴OD=CE=(OC-AB)÷2=1.
∵AO=2,∴AD==,∴A(1,).
∵OE=OD+DE=1+3=4,BE=AD=,∴B(4,).
∵BC=2EC,∴∠EBC=30°,∴∠OCB=60°.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,∴S扫==.
(3)分三种情况讨论:①当0≤t<2时,如图1,△AEF∽△AOD,,∴S扫t2;
②当2≤t<3时,如图2,S扫=S△AOD+S□DOPF(t﹣2),∴S扫;
③当3≤t≤7时,如图3,过B作直线EB∥直线l交OC于E.
∵∠BEC=30°,∠OCB=60°,∴∠CBE=90°,∴EC=2BC=4,∴S△CEB=,CP=7-t.
∵MP∥BE,∴,∴S△CPM=,∴S扫=4S△CPM=4,∴S扫t2
综上所述: .
∵t2,∴t2﹣14t+41=0,t1=7﹣2,t2=7+27(舍),∴P的坐标为(5﹣2,0).
【点睛】本题考查了梯形的性质,相似三角形的判定和性质,二次函数的综合应用等知识点.主要考查了学生分类讨论和数形结合的数学思想方法.
20.(1),顶点坐标为(2,1).
(2)详见解析
【分析】(1)利用交点式得出,从而得出a求出的值,再利用配方法求出顶点坐标即可.
(2)根据左加右减得出抛物线的解析式为y=-x2,从而得出答案,答案不唯一.
【详解】解:(1)∵抛物线与x轴交于点A(1,0),B(3,0),
∴可设抛物线解析式为.
把C(0,-3)代入得:3a=-3,解得:a=-1.
∴抛物线解析式为,即.
∵,
∴顶点坐标为(2,1).
(2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=﹣x2,
平移后抛物线的顶点为(0,0)落在直线y=-x上.
21.(1) 当40≤x<60时,W=-2x2+200x-4200,当60≤x≤70时,W=-x2+110x-2400;(2) 该产品的售价为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元.
【分析】(1)根据:年利润=(售价-成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案.
【详解】(1)当40≤x<60时,W=(x-30)(-2x+140)=-2x2+200x-4200,
当60≤x≤70时,W=(x-30)(-x+80)=-x2+110x-2400;
(2)当40≤x<60时,W=-2x2+200x-4200=-2(x-50)2+800,
∴当x=50时,W取得最大值,最大值为800万元;
当60≤x≤70时,W=-x2+110x-2400=-(x-55)2+625,
∴当x>55时,W随x的增大而减小,
∴当x=60时,W取得最大值,最大值为:-(60-55)2+625=600,
∵800>600,
∴当x=50时,W取得最大值800,
答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元.
【点睛】本题主要考查了二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.
22.(1)(0,1);1或0 (2) (3)
【分析】(1)由题意,可得点B坐标,进而求得直线的解析式,再分情况讨论即可解的m值;
(2)由非负性解得m和b的值,进而得到两个函数解析式,设与x轴、y轴交于T,P,分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
(3)先根据解析式,用m表示出点C、E、D的坐标以及y关于x的表达式为,得知y是关于x的二次函数且开口向上、最低点为其顶点,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:,较小的可为平行于DE且与抛物线相切时围成的图形面积.
【详解】解:(1)由题意可得点B坐标为(0,1),
设直线的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
所以直线的表达式为:y=x+1,
若直线恰好是的图象,则2m-1=1,解得:m=1,
若直线恰好是的图象,则2m+1=1,解得:m=0,
综上,,或者
(2)如图,
,
,
,
设与x轴、y轴交于T,P,分别与x轴、y轴交于G,H,连接GP,TH
,
四边形GPTH是正方形
,,即
;
(3),
分别交x轴,y轴于C,E两点
,
图象交x轴于D点
二次函数开口向上,它的图象最低点在顶点
顶点
抛物线顶点F向上平移,刚好在一次函数图象上
且
,
∴,
由,得到,,
由得到与x轴,y轴交点是,,,
抛物线经过,两点
的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
探究办法:利用规则图形面积来估算不规则图形的面积.
探究过程:
①观察大于S的情况.
很容易发现
,
,
(若有S小于其他值情况,只要合理,参照赋分.)
②观察小于S的情况.
选取小于S的几个特殊值来估计更精确的S的近似值,取值会因人而不同,下面推荐一种方法,选取以下三种特殊位置:
位置一:如图
当直线MN与DE平行且与抛物线有唯一交点时,设直线MN与x,y轴分别交于M,N
,
直线
设直线
,
直线
点
,
位置二:如图
当直线DR与抛物线有唯一交点时,直线DR与y轴交于点R
设直线,
直线
,
直线
点
,
位置三:如图
当直线EQ与抛物线有唯一交点时,直线EQ与x轴交于点Q
设直线
,
直线
点
,
我们发现:在曲线DE两端位置时的三角形的面积远离S的值,由此估计在曲线DE靠近中间部分时取值越接近S的值
探究的结论:按上述方法可得一个取值范围
(备注:不同的探究方法会有不同的结论,因而会有不同的答案.只要来龙去脉清晰、合理,即可参照赋分,但若直接写出一个范围或者范围两端数值的差不在0.01之间不得分.)
【点睛】本题是一道综合性很强的代数与几何相结合的压轴题,知识面广,涉及有旋转的性质、坐标平移规则、非负数的性质、一次函数的图象与性质、二次函数的图象与性质、一元二次方程、不规则图形面积的估计等知识,解答的关键是认真审题,找出相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,利用相关信息进行推理、探究、发现和计算.
23.(1)y=﹣x2+x+1;(2)S=﹣t2+t+;(3)点N的坐标为(1,2)
【分析】(1)设抛物线的解析式为y=ax2+bx+c,然后利用待定系数法即可得;
(2)当﹣<t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
(3)根据相似三角形的性质可得PN=2PO,由于PN=﹣t2+t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
【详解】解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得: ,
解得:,
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,
∴,
∴,
∴PN=2PO,
当0<t<2时,PN=|yN|=yN=﹣t2+t+1,PO=|t|=t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t1=﹣,t2=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2),
故点N的坐标为(1,2).
【点睛】本题考查了二次函数与几何综合题,涉及了待定系数法、相似三角形的性质、解一元二次方程等,综合性较强,有一定的难度,解本题需要注意的是:用点的坐标表示线段长度时,应该用绝对值表示线段的长度,根据坐标的正负化简绝对值,解方程的要进行检验,不符合条件的要舍去,熟练掌握和灵活运用相关知识是解题的关键.
24.(1);(2)w有最小值是;(3)t的值为3﹣或4+.
【分析】(1)根据“和谐点”的坐标特征设出坐标,代入双曲线中,有解则有“和谐点”;
(2)设抛物线“和谐点”的坐标为,代入抛物线的关系式中得到关于x的一元二次方程,因为有两个“和谐点”,则这两个“和谐点”的横坐标就是这个一元二次方程的两个根,再由根与系数的关系得:两根和与两根据积的式子,得到w关于a的二次函数,求最小值即可;
(3)设函数“和谐点”的坐标为,代入函数的关系式中得到关于x的一元二次方程,因为有一个“和谐点”,则,得到n=(m﹣t)2﹣t+2,把它看成一个二次函数,对称轴m=t,分三种情况讨论即可.
【详解】解:(1)设“和谐点”的坐标为,
将点坐标代入直线y=3x﹣2得:t=3t﹣2,
解得:t=1,
故“和谐点”的坐标为;
(2)设抛物线“和谐点”的坐标为,
代入抛物线y=﹣x2+(a+1)x﹣a+1中得:
x=﹣x2+(a+1)x﹣a+1,
﹣x2+ax﹣a+1=0,
∵“和谐点”为和,
∴x1、x2是方程﹣x2+ax﹣a+1=0的两个根,
则x1+x2=﹣=,x1 x2==2a﹣2,
w=x12+x22=(x1+x2)2﹣2x1x2=()2﹣2(2a﹣2),
w=﹣4a+4=(a﹣)2+,
∵>0,
∴抛物线开口向上当a=时,w有最小值是;
(3)设函数“和谐点”的坐标为,
代入函数y=x2+(m﹣t+1)x+n+t﹣2得:
x=x2+(m﹣t+1)x+n+t﹣2,
x2+(m﹣t)x+n+t﹣2=0,
∵存在唯一的一个“和谐点”,
∴=(m﹣t)2﹣4××(n+t﹣2)=0,
n=(m﹣t)2﹣t+2,
这是一个n关于m的二次函数,图象为抛物线,开口向上,对称轴为m=t,对称轴左侧,n随m的增大而减小;对称轴右侧,n随m的增大而增大;
①t<2,当2≤m≤3时,在对称轴右侧递增,
∴当m=2时,n有最小值为t,
即(2﹣t)2﹣t+2=t,
t2﹣6t+6=0,
解得:t1=3+>2(舍去),t2=3﹣,
②t>3,当2≤m≤3时,在对称轴左侧递减,
∴当m=3时,n有最小值为t,
即(3﹣t)2﹣t+2=t,
解得:t1=4+,t2=4﹣<3(舍),
③当2≤t≤3,当2≤m≤3时,n有最小值为﹣t+2,
∴﹣t+2=t,
t=1<2(舍去),
综上所以述:t的值为3﹣或4+.
【点睛】本题考查了二次函数的性质及一元二次方程的根与二次函数的关系;明确一元二次方程根据与系数的关系,方程的解与根的判别式的关系;尤其是二次函数的最值问题,在自变量的所有取值中:①当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,函数有最小值;②当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,函数有最大值;如果在规定的取值中,要看图象和增减性来判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.7二次函数的应用
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.下列结论:①小球在空中经过的路程是;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度时,.其中正确的是( )
A.①④ B.①② C.②③④ D.②③
2.如图,直线与两坐标轴交于A,B两点,点P是线段AB上一动点(不与A,B两端点重合),过点P作PC⊥x轴于点C,作PD⊥y轴于点D,小明认为矩形PCOD的周长不变且始终为6;小红认为矩形PCOD的面积有最大值,最大值为3.关于小明与小红的判断,下面说法正确的是( )
A.小明与小红都是正确的 B.小明与小红都是错误的
C.小明是正确的,小红是错误的 D.小明是错误的,小红是正确的
3.跳台滑雪是冬季奥运会比赛项目之一.运动员起跳后的飞行路线可以看作是抛物线的一部分,运动员起跳后的竖直高度(单位:)与水平距离(单位:)近似满足函数关系().下图记录了某运动员起跳后的与的三组数据,根据上述函数模型和数据,可推断出该运动员起跳后飞行到最高点时,水平距离为
A. B. C. D.
4.某农场用篱笆围成饲养室,一面靠现有墙(墙足够长),现有四种方案供选择(如图):
A方案为一个封闭的矩形;
B方案为一个等边三角形,并留一处宽的门;
C方案为一个矩形,中间用一道垂直于墙的篱笆隔开,并在如图所示的三处各留宽的门;
D方案为一个矩形,中间用一道平行于墙的篱笆隔开,并在如图所示的四处各留宽的门.已知计划中的篱笆(不包括门)总长为,则能建成的饲养室中面积最大的方案为( )
A. B. C. D.
5.如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣x2刻画,斜坡可以用一次函数y=x刻画,下列结论错误的是( )
A.当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B.小球距O点水平距离超过4米呈下降趋势
C.小球落地点距O点水平距离为7米
D.斜坡的坡度为1:2
6.某种产品按质量分为个档次,生产最低档次产品,每件获利润元,每提高一个档次,每件产品利润增加元,用同样工时,最低档次产品每天可生产件,提高一个档次将减少件.如果用相同的工时生产,总获利润最大的产品是第档次(最低档次为第一档次,档次依次随质量增加),那么等于( )
A. B. C. D.
7.竖直向上发射的小球的高度关于运动时间的函数表达式为,其图象如图所示,若小球发射后第2秒与第6秒时的高度相等,则下列时刻中小球的高度最高的是( )
A.第3秒 B.第3.5秒 C.第4秒 D.第6秒
8.如图,在△ABC中,∠B=90°,AB=6cm,BC=12cm,动点P从点A开始沿边AB向B以1cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向C以2cm/s的速度移动(不与点C重合).如果P、Q分别从A、B同时出发,那么经过( )秒,四边形APQC的面积最小.
A.1 B.2 C.3 D.4
9.如图,在Rt△ABC中,∠C=90°,AC=BC,E是AB的中点,过点E作AC和BC的垂线,垂足分别为D和点F,四边形CDEF沿着CA方向匀速运动,点C与点A重合时停止运动,设运动时间为t,则S关于t的函数图象大致为( )
A. B.
C. D.
10.如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=6cm,动点P从点C沿CA,以1cm/s的速度向点A运动,同时动点O从点C沿CB,以2cm/s的速度向点B运动,其中一个动点到达终点时,另一个动点也停止运动.则运动过程中所构成的△CPO的面积y(cm2)与运动时间x(s)之间的函数图象大致是( )
A. B. C. D.
11.太阳影子定位技术是通过分析视频中物体的太阳影子变化,确定视频拍摄地点的一种方法为了确定视频拍摄地的经度,我们需要对比视频中影子最短的时刻与同一天东经120度影子最短的时刻在一定条件下,直杆的太阳影子长度单位:米与时刻单位:时的关系满足函数关系是常数,如图记录了三个时刻的数据,根据上述函数模型和记录的数据,则该地影子最短时,最接近的时刻t是()
A. B.13 C. D.
12.如图,抛物线交x轴的负半轴于点A,点B是y轴的正半轴上一点,点A关于点B的对称点A 恰好落在抛物线上.过点A 作x轴的平行线交抛物线于另一点C,则点A 的纵坐标为()
A.1.5 B.2 C.2.5 D.3
二、填空题
13.为庆祝嫦娥五号登月成功,某工艺厂生产了一款纪念品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就多售出5件,但要求销售单价不得低于成本.则该工艺厂将每件的销售价定为 元时,可使每天所获销售利润最大.
14.某厂有一种产品现在的年产量是2万件,计划今后两年增加产量,如果每年都比上一年的产量增加x倍,那么两年后这种产品的产量y(万件)将随计划所定的x的值而确定,那么y与x之间的关系式应表示为 .
15.如图,在平面直角坐标系中,点A(4,8)在抛物线上,过点A作y轴的垂线,交抛物线于另一点B,点C、D在线段AB上,分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时,线段CD的长为 .
16.为了让农民能种植高产、易发芽的种子,某农科实验基地大力开展种子实验.该实验基地两年前有100种种子,经过两年不断地努力,现在已有144种种子.若培育的种子平均每年的增长率为x,则x的值为 .
17.某网店某种商品成本为50元/件,售价为60元/件时,每天可销售100件;售价单价高于60元时,每涨价1元,日销售量就减少2件.据此,当销售单价为 元时,网店该商品每天盈利最多.
三、解答题
18.如图,已知抛物线的对称轴为直线,且抛物线与轴交于、两点,与轴交于点,其中,.
(1)若直线经过、两点,求直线和抛物线的解析式;
(2)在抛物线的对称轴上找一点,使点到点的距离与到点的距离之和最小,求出点的坐标;
(3)设点为抛物线的对称轴上的一个动点,求使为直角三角形的点的坐标.
19.如图,在直角坐标系xOy中有一梯形ABCO,顶点C在x正半轴上,A、B两点在第一象限;且AB∥CO,AO=BC=2,AB=3,OC=5.点P在x轴上,从点(﹣2,0)出发,以每秒1个单位长度的速度沿x轴向正方向运动;同时,过点P作直线l,使直线l和x轴向正方向夹角为30°.设点P运动了t秒,直线l扫过梯形ABCO的面积为S扫.
(1)求A、B两点的坐标;
(2)当t=2秒时,求S扫的值;
(3)求S扫与t的函数关系式,并求出直线l扫过梯形ABCO面积的时点P的坐标.
20.已知抛物线与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.
21.某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数表达式为
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数表达式;
(2)当该产品的售价为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
22.已知函数均为一次函数,m为常数.
(1)如图1,将直线绕点逆时针旋转45°得到直线,直线交y轴于点B.若直线恰好是中某个函数的图象,请直接写出点B坐标以及m可能的值;
(2)若存在实数b,使得成立,求函数图象间的距离;
(3)当时,函数图象分别交x轴,y轴于C,E两点,图象交x轴于D点,将函数的图象最低点F向上平移个单位后刚好落在一次函数图象上,设的图象,线段,线段围成的图形面积为S,试利用初中知识,探究S的一个近似取值范围.(要求:说出一种得到S的更精确的近似值的探究办法,写出探究过程,得出探究结果,结果的取值范围两端的数值差不超过0.01.)
23.如图,抛物线与x轴交于点A(﹣, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
24.已知y是关于x的函数,若其函数图象经过点P(t,t),则称点P为函数图象上的“和谐点”.
(1)求出直线y=3x﹣2的“和谐点”坐标;
(2)若抛物线y=﹣x2+(a+1)x﹣a+1上有“和谐点”,且“和谐点”为A(x1,y1)和B(x2,y2),求W=x12+x22的最小值;
(3)若函数y=x2+(m﹣t+1)x+n+t﹣2的图象上存在唯一的一个“和谐点”且当2≤m≤3时,n的最小值为t,求t的值.
《5.7二次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B C A C C C C C
题号 11 12
答案 C B
1.D
【分析】根据函数的图象中的信息判断即可.
【详解】①由图象知小球在空中达到的最大高度是;故①错误;
②小球抛出3秒后,速度越来越快;故②正确;
③小球抛出3秒时达到最高点即速度为0;故③正确;
④设函数解析式为:,
把代入得,解得,
∴函数解析式为,
把代入解析式得,,
解得:或,
∴小球的高度时,或,故④错误;
故选D.
【点睛】本题考查了二次函数的应用,解此题的关键是正确的理解题意
2.C
【分析】设P(x,)().根据周长公式求出周长,即可判定小明的正误;根据面积公式求出面积,结合二次函数的性质,即可判断小红的正误.
【详解】设P(x,)(),
∵,
∴周长不变,且始终为6,即小明正确;
∵,
∴当时,最大,最大为,即小红是错误的.
故选C
【点睛】本题考查一次函数与二次函数的综合.掌握二次函数的性质是解题关键.
3.B
【详解】分析: 根据抛物线的对称性即可判断出对称轴的范围.
详解:设对称轴为,
由(,)和(,)可知,,
由(,)和(,)可知,,
∴,
故选B.
点睛:考查抛物线的对称性,熟练运用抛物线的对称性质是解题的关键.
4.C
【分析】设建成的饲养室的面积为,先根据篱笆总长、矩形与等边三角形的面积公式求出的函数关系式,再利用二次函数的性质求最值,然后比较大小即可得.
【详解】设建成的饲养室的面积为,
对于A选项,如图(1),设边的长为,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为18;
对于B选项,如图(2),设,则,解得,
由等边三角形的性质得:AB边上的高为,
则;
对于C选项,如图(3),设,则,,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为;
对于D选项,如图(4),设,则,
,
,
由矩形的面积公式得:,
则在范围内,当时,取得最大值,最大值为16;
因为,
所以建成的饲养室中面积最大的方案是C方案,
故选:C.
【点睛】本题考查了二次函数的应用、矩形与等边三角形的面积公式,依据题意,分别求出各图形的面积的函数表达式是解题关键.
5.A
【分析】求出当y=7.5时,x的值,判定选项A;根据二次函数的性质求出对称轴,根据二次函数性质判断选项B;求出抛物线与直线的交点,判断选项C,根据直线解析式和坡度的定义判断选项D.
【详解】当y=7.5时,7.5=4x﹣x2,
整理得x2﹣8x+15=0,
解得,x1=3,x2=5,
∴当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m或5cm,选项A错误,符合题意;
y=4x﹣x2
=﹣(x﹣4)2+8,
则抛物线的对称轴为x=4,
∴当x>4时,y随x的增大而减小,即小球距O点水平距离超过4米呈下降趋势,选项B正确,不符合题意;
,
解得,,,
则小球落地点距O点水平距离为7米,选项C正确,不符合题意;
∵斜坡可以用一次函数y=x刻画,
∴斜坡的坡度为1:2,选项D正确,不符合题意;
故选A.
【点睛】本题考查的是解直角三角形的——坡度问题、二次函数的性质,掌握坡度的概念、二次函数的性质是解题的关键.
6.C
【分析】第档次产品比最低档次产品提高了个档次,则数量在60的基础上减少了,每件产品利润在8的基础上增加,据此可求出总利润关系,求出最值即可.
【详解】解:设总利润为y元,
∵第档次产品比最低档次产品提高了个档次,
∴每天利润为,
∴当时,产品利润最大,每天获利864元,
故选C.
【点睛】本题考查了二次函数的实际应用,借助二次函数解决实际问题是本题的关键.
7.C
【分析】根据题中已知条件求出函数h=at2+bt的对称轴t=4,在t=4s时,小球的高度最高.
【详解】解:由题意可知:小球发射后第2秒与第6秒时的高度相等,
即4a+2b=36a+6b,
解得b=﹣8a,
函数h=at2+bt的对称轴t=﹣=4,
故在t=4s时,小球的高度最高,
故选:C.
【点睛】本题主要考查了二次函数的实际应用,求出抛物线对称轴是解题关键.
8.C
【分析】根据等量关系“四边形APQC的面积=三角形ABC的面积-三角形PBQ的面积”列出函数关系求最小值.
【详解】解:设P、Q同时出发后经过的时间为ts,四边形APQC的面积为Scm2,则有:
S=S△ABC-S△PBQ
= ×12×6- (6-t)×2t
=t2-6t+36
=(t-3)2+27.
∴当t=3s时,S取得最小值.
故选C.
【点睛】本题考查了函数关系式的求法以及最值的求法,解题的关键是根据题意列出函数关系式,并根据二次函数的性质求出最值.
9.C
【分析】根据已知条件得到△ABC是等腰直角三角形,推出四边形EFCD是正方形,设正方形的边长为a,当移动的距离
【详解】解:∵在直角三角形ABC中,∠C=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵EF⊥BC,ED⊥AC,
∴四边形EFCD是矩形,
∵E是AB的中点,
∴EF=AC,DE=BC,
∴EF=ED,
∴四边形EFCD是正方形,
设正方形的边长为a,如图1,当移动的距离
∴S关于t的函数图象大致为C选项,故选:C.
【点睛】本题考查动点问题的函数图象,正方形的性质、勾股定理等知识,解题的关键是读懂题意,学会分类讨论的思想,属于中考常考题型.
10.C
【详解】试题分析:解决本题的关键是正确确定y与x之间的函数解析式.
解:∵运动时间x(s),则CP=x,CO=2x;
∴S△CPO=CP CO=x 2x=x2.
∴则△CPO的面积y(cm2)与运动时间x(s)之间的函数关系式是:y=x2(0≤x≤3),
故选C.
考点:动点问题的函数图象;二次函数的图象.
11.C
【详解】把(12,0.6)、(13,0.35)、(14,0.4)代入l=at2+bt+c中得:
,解得,
∴l=0.15t2-4t+27,
∵0.15>0,
∴l有最小值,
当t=-=≈13.33时,该地影子最短;
故选C.
【点睛】错因分析 中等题.失分原因:没有理解本题考查的真正意图,通过二次函数图象上的点结合函数性质,推断对称轴位置.
12.B
【分析】先求出点A坐标,利用对称可得点横坐标,代入可得纵坐标.
【详解】解:令得,即
解得
点B是y轴的正半轴上一点,点A关于点B的对称点A 恰好落在抛物线上
点的横坐标为1
当时,
所以点A 的纵坐标为2.
故选:B
【点睛】本题考查了二次函数的图像,熟练利用函数解析式求点的坐标是解题的关键.
13.80
【分析】根据每天获得利润=单件利润×销售量列出二次函数即可求解.
【详解】解:设销售单价降低x元时,则销售单价是(100-x)元时,每天获利y元.
根据题意,得
y=(100-50-x)(50+5x)
=-5x2+200x+2500
=-5(x-20)2+4500
∵-5<0,当x=20时,y有最大值,
即100-x=80,80>50,
答:当销售单价是80元时,每天获利最多.
故答案为80.
【点睛】本题考查了二次函数的应用,解决本题的关键是掌握销售问题的数量关系.
14.或
【分析】根据平均增长问题,可得答案.
【详解】解:y与x之间的关系应表示为y=2(x+1)2.
故答案为:y=2(x+1)2.
【点睛】本题考查了函数关系式,利用增长问题获得函数解析式是解题关键,注意增加x倍是原来的(x+1)倍.
15.
【分析】利用待定系数法求出函数解析式,然后设点C横坐标为m,则CD=CE=2m,从而得出点E坐标为(m,8 2m),将点E坐标代入解析式求出m即可解决问题.
【详解】解:把A(4,8)代入中得8=16a,
解得a=,
∴,
设点C横坐标为m,则CD=CE=2m,
∴点E坐标为(m,8﹣2m),
∴=8﹣2m,
解得m=(舍)或m=,
∴CD=2m=,
故答案为:.
【点睛】本题考查二次函数的应用,待定系数法,解题关键是设出点C横坐标,表示出点E的坐标.
16.20%
【分析】利用该实验基地现在拥有的种子种数=该实验基地两年前拥有的种子种数×(1+培育的种子平均每年的增长率)2,可得出关于x的一元二次方程,解之取其符合题意的值,即可得出结论.
【详解】解:根据题意得:,
解得:(不符合题意,舍去),
∴x的值为.
故答案为:.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
17.80
【分析】直接利用每件利润×销量=总利润,进而得出每天盈利与x的关系式,配方即可得出答案.
【详解】解:设当销售单价为x元时,每天盈利为y元,
则y=(x-50)[100-2(x-60)]
=-2x2+320x-11000
=-2(x-80)2+1800,
∵-2<0,
∴当x=80时,y有最大值,且为1800,
答:当销售单价为80元时,每天获取的利润最大,最大利润是1800元.
【点睛】此题主要考查了二次函数的应用,正确得出函数关系式是解题关键.
18.(1)抛物线的解析式为,直线的解析式为.(2);(3)的坐标为或或或.
【详解】分析:(1)先把点A,C的坐标分别代入抛物线解析式得到a和b,c的关系式,再根据抛物线的对称轴方程可得a和b的关系,再联立得到方程组,解方程组,求出a,b,c的值即可得到抛物线解析式;把B、C两点的坐标代入直线y=mx+n,解方程组求出m和n的值即可得到直线解析式;
(2)设直线BC与对称轴x=-1的交点为M,此时MA+MC的值最小.把x=-1代入直线y=x+3得y的值,即可求出点M坐标;
(3)设P(-1,t),又因为B(-3,0),C(0,3),所以可得BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,再分三种情况分别讨论求出符合题意t值即可求出点P的坐标.
详解:(1)依题意得:,解得:,
∴抛物线的解析式为.
∵对称轴为,且抛物线经过,
∴把、分别代入直线,
得,解之得:,
∴直线的解析式为.
(2)直线与对称轴的交点为,则此时的值最小,把代入直线得,
∴.即当点到点的距离与到点的距离之和最小时的坐标为.
(注:本题只求坐标没说要求证明为何此时的值最小,所以答案未证明的值最小的原因).
(3)设,又,,
∴,,,
①若点为直角顶点,则,即:解得:,
②若点为直角顶点,则,即:解得:,
③若点为直角顶点,则,即:解得:
,.
综上所述的坐标为或或或.
点睛:本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式、利用轴对称性质确定线段的最小长度、难度不是很大,是一道不错的中考压轴题.
19.(1)(1,),(4,);(2);(3);P的坐标为(5﹣2,0).
【分析】(1)两底的差的一半就是A的横坐标;过A、B作x轴的垂线,在构建的直角三角形中根据OA的长及两底的差便可求出梯形的高即A点的纵坐标.得出A点坐标后向右平移3个单位就是B点的坐标.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,由此可求出△ADO的面积及直线l扫过的面积.
(3)本题要分三种情况进行讨论:
①当P在原点左侧,即当0≤t<2时,重合部分是个三角形,如果设直线l与AO,AB分别交于E,F,可根据△AEF∽△AOD,用相似比求出其面积.即可得出S,t的函数关系式.
②当P在O点右侧(包括和O重合),而F点在B点左侧时,即当2≤t<3时,扫过部分是个梯形,可根据梯形的面积计算方法即可得出直线l扫过部分的面积.也就能得出S,t的函数关系式.
③当P点在C点左侧(包括和C点重合),F点在B点右侧(包括和B点重合),即当3≤t≤7时,扫过部分是个五边形,可用梯形ABCO的面积减去△MPC的面积来得出S,t的函数关系式.
【详解】(1)过A作AD⊥OC于D,过B作BE⊥OC于E,则ADEB是矩形.
∵ADEB是矩形,∴AD=BE=3.
∵AO=BC,∴△AOD≌△BCE,∴OD=CE=(OC-AB)÷2=1.
∵AO=2,∴AD==,∴A(1,).
∵OE=OD+DE=1+3=4,BE=AD=,∴B(4,).
∵BC=2EC,∴∠EBC=30°,∴∠OCB=60°.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,∴S扫==.
(3)分三种情况讨论:①当0≤t<2时,如图1,△AEF∽△AOD,,∴S扫t2;
②当2≤t<3时,如图2,S扫=S△AOD+S□DOPF(t﹣2),∴S扫;
③当3≤t≤7时,如图3,过B作直线EB∥直线l交OC于E.
∵∠BEC=30°,∠OCB=60°,∴∠CBE=90°,∴EC=2BC=4,∴S△CEB=,CP=7-t.
∵MP∥BE,∴,∴S△CPM=,∴S扫=4S△CPM=4,∴S扫t2
综上所述: .
∵t2,∴t2﹣14t+41=0,t1=7﹣2,t2=7+27(舍),∴P的坐标为(5﹣2,0).
【点睛】本题考查了梯形的性质,相似三角形的判定和性质,二次函数的综合应用等知识点.主要考查了学生分类讨论和数形结合的数学思想方法.
20.(1),顶点坐标为(2,1).
(2)详见解析
【分析】(1)利用交点式得出,从而得出a求出的值,再利用配方法求出顶点坐标即可.
(2)根据左加右减得出抛物线的解析式为y=-x2,从而得出答案,答案不唯一.
【详解】解:(1)∵抛物线与x轴交于点A(1,0),B(3,0),
∴可设抛物线解析式为.
把C(0,-3)代入得:3a=-3,解得:a=-1.
∴抛物线解析式为,即.
∵,
∴顶点坐标为(2,1).
(2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=﹣x2,
平移后抛物线的顶点为(0,0)落在直线y=-x上.
21.(1) 当40≤x<60时,W=-2x2+200x-4200,当60≤x≤70时,W=-x2+110x-2400;(2) 该产品的售价为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元.
【分析】(1)根据:年利润=(售价-成本)×年销售量,结合x的取值范围可列函数关系式;
(2)将(1)中两个二次函数配方后依据二次函数的性质可得其最值情况,比较后可得答案.
【详解】(1)当40≤x<60时,W=(x-30)(-2x+140)=-2x2+200x-4200,
当60≤x≤70时,W=(x-30)(-x+80)=-x2+110x-2400;
(2)当40≤x<60时,W=-2x2+200x-4200=-2(x-50)2+800,
∴当x=50时,W取得最大值,最大值为800万元;
当60≤x≤70时,W=-x2+110x-2400=-(x-55)2+625,
∴当x>55时,W随x的增大而减小,
∴当x=60时,W取得最大值,最大值为:-(60-55)2+625=600,
∵800>600,
∴当x=50时,W取得最大值800,
答:该产品的售价x为50元/件时,企业销售该产品获得的年利润最大,最大年利润是800万元.
【点睛】本题主要考查了二次函数的实际应用,梳理题目中的数量关系,得出相等关系后分情况列出函数解析式,熟练运用二次函数性质求最值是解题的关键.
22.(1)(0,1);1或0 (2) (3)
【分析】(1)由题意,可得点B坐标,进而求得直线的解析式,再分情况讨论即可解的m值;
(2)由非负性解得m和b的值,进而得到两个函数解析式,设与x轴、y轴交于T,P,分别与x轴、y轴交于G,H,连接GP,TH,证得四边形GPTH是正方形,求出GP即为距离;
(3)先根据解析式,用m表示出点C、E、D的坐标以及y关于x的表达式为,得知y是关于x的二次函数且开口向上、最低点为其顶点,根据坐标平移规则,得到关于m的方程,解出m值,即可得知点D 、E的坐标且抛物线过D、E点,观察图象,即可得出S的大体范围,如:,较小的可为平行于DE且与抛物线相切时围成的图形面积.
【详解】解:(1)由题意可得点B坐标为(0,1),
设直线的表达式为y=kx+1,将点A(-1,0)代入得:k=1,
所以直线的表达式为:y=x+1,
若直线恰好是的图象,则2m-1=1,解得:m=1,
若直线恰好是的图象,则2m+1=1,解得:m=0,
综上,,或者
(2)如图,
,
,
,
设与x轴、y轴交于T,P,分别与x轴、y轴交于G,H,连接GP,TH
,
四边形GPTH是正方形
,,即
;
(3),
分别交x轴,y轴于C,E两点
,
图象交x轴于D点
二次函数开口向上,它的图象最低点在顶点
顶点
抛物线顶点F向上平移,刚好在一次函数图象上
且
,
∴,
由,得到,,
由得到与x轴,y轴交点是,,,
抛物线经过,两点
的图象,线段OD,线段OE围成的图形是封闭图形,则S即为该封闭图形的面积
探究办法:利用规则图形面积来估算不规则图形的面积.
探究过程:
①观察大于S的情况.
很容易发现
,
,
(若有S小于其他值情况,只要合理,参照赋分.)
②观察小于S的情况.
选取小于S的几个特殊值来估计更精确的S的近似值,取值会因人而不同,下面推荐一种方法,选取以下三种特殊位置:
位置一:如图
当直线MN与DE平行且与抛物线有唯一交点时,设直线MN与x,y轴分别交于M,N
,
直线
设直线
,
直线
点
,
位置二:如图
当直线DR与抛物线有唯一交点时,直线DR与y轴交于点R
设直线,
直线
,
直线
点
,
位置三:如图
当直线EQ与抛物线有唯一交点时,直线EQ与x轴交于点Q
设直线
,
直线
点
,
我们发现:在曲线DE两端位置时的三角形的面积远离S的值,由此估计在曲线DE靠近中间部分时取值越接近S的值
探究的结论:按上述方法可得一个取值范围
(备注:不同的探究方法会有不同的结论,因而会有不同的答案.只要来龙去脉清晰、合理,即可参照赋分,但若直接写出一个范围或者范围两端数值的差不在0.01之间不得分.)
【点睛】本题是一道综合性很强的代数与几何相结合的压轴题,知识面广,涉及有旋转的性质、坐标平移规则、非负数的性质、一次函数的图象与性质、二次函数的图象与性质、一元二次方程、不规则图形面积的估计等知识,解答的关键是认真审题,找出相关信息,利用待定系数法、数形结合法等解题方法确定解题思路,利用相关信息进行推理、探究、发现和计算.
23.(1)y=﹣x2+x+1;(2)S=﹣t2+t+;(3)点N的坐标为(1,2)
【分析】(1)设抛物线的解析式为y=ax2+bx+c,然后利用待定系数法即可得;
(2)当﹣<t<2时,点N在x轴上方,则NP等于点N的纵坐标,求出AB的长,然后利用三角形面积公式即可得;
(3)根据相似三角形的性质可得PN=2PO,由于PN=﹣t2+t+1,PO=|t|=t,可得关于t的方程,解这个方程即可解决这个问题.
【详解】解:(1)设抛物线的解析式为y=ax2+bx+c,由题意可得: ,
解得:,
∴抛物线的函数关系式为y=﹣x2+x+1;
(2)当﹣<t<2时,yN>0,
∴NP=|yN|=yN=﹣t2+t+1,
∴S=AB PN
=×(2+)×(﹣t2+t+1)
=(﹣t2+t+1)
=﹣t2+t+;
(3)∵△OPN∽△COB,
∴,
∴,
∴PN=2PO,
当0<t<2时,PN=|yN|=yN=﹣t2+t+1,PO=|t|=t,
∴﹣t2+t+1=2t,
整理得:3t2﹣t﹣2=0,
解得:t1=﹣,t2=1.
∵﹣<0,0<1<2,
∴t=1,此时点N的坐标为(1,2),
故点N的坐标为(1,2).
【点睛】本题考查了二次函数与几何综合题,涉及了待定系数法、相似三角形的性质、解一元二次方程等,综合性较强,有一定的难度,解本题需要注意的是:用点的坐标表示线段长度时,应该用绝对值表示线段的长度,根据坐标的正负化简绝对值,解方程的要进行检验,不符合条件的要舍去,熟练掌握和灵活运用相关知识是解题的关键.
24.(1);(2)w有最小值是;(3)t的值为3﹣或4+.
【分析】(1)根据“和谐点”的坐标特征设出坐标,代入双曲线中,有解则有“和谐点”;
(2)设抛物线“和谐点”的坐标为,代入抛物线的关系式中得到关于x的一元二次方程,因为有两个“和谐点”,则这两个“和谐点”的横坐标就是这个一元二次方程的两个根,再由根与系数的关系得:两根和与两根据积的式子,得到w关于a的二次函数,求最小值即可;
(3)设函数“和谐点”的坐标为,代入函数的关系式中得到关于x的一元二次方程,因为有一个“和谐点”,则,得到n=(m﹣t)2﹣t+2,把它看成一个二次函数,对称轴m=t,分三种情况讨论即可.
【详解】解:(1)设“和谐点”的坐标为,
将点坐标代入直线y=3x﹣2得:t=3t﹣2,
解得:t=1,
故“和谐点”的坐标为;
(2)设抛物线“和谐点”的坐标为,
代入抛物线y=﹣x2+(a+1)x﹣a+1中得:
x=﹣x2+(a+1)x﹣a+1,
﹣x2+ax﹣a+1=0,
∵“和谐点”为和,
∴x1、x2是方程﹣x2+ax﹣a+1=0的两个根,
则x1+x2=﹣=,x1 x2==2a﹣2,
w=x12+x22=(x1+x2)2﹣2x1x2=()2﹣2(2a﹣2),
w=﹣4a+4=(a﹣)2+,
∵>0,
∴抛物线开口向上当a=时,w有最小值是;
(3)设函数“和谐点”的坐标为,
代入函数y=x2+(m﹣t+1)x+n+t﹣2得:
x=x2+(m﹣t+1)x+n+t﹣2,
x2+(m﹣t)x+n+t﹣2=0,
∵存在唯一的一个“和谐点”,
∴=(m﹣t)2﹣4××(n+t﹣2)=0,
n=(m﹣t)2﹣t+2,
这是一个n关于m的二次函数,图象为抛物线,开口向上,对称轴为m=t,对称轴左侧,n随m的增大而减小;对称轴右侧,n随m的增大而增大;
①t<2,当2≤m≤3时,在对称轴右侧递增,
∴当m=2时,n有最小值为t,
即(2﹣t)2﹣t+2=t,
t2﹣6t+6=0,
解得:t1=3+>2(舍去),t2=3﹣,
②t>3,当2≤m≤3时,在对称轴左侧递减,
∴当m=3时,n有最小值为t,
即(3﹣t)2﹣t+2=t,
解得:t1=4+,t2=4﹣<3(舍),
③当2≤t≤3,当2≤m≤3时,n有最小值为﹣t+2,
∴﹣t+2=t,
t=1<2(舍去),
综上所以述:t的值为3﹣或4+.
【点睛】本题考查了二次函数的性质及一元二次方程的根与二次函数的关系;明确一元二次方程根据与系数的关系,方程的解与根的判别式的关系;尤其是二次函数的最值问题,在自变量的所有取值中:①当a>0时,抛物线在对称轴左侧,y随x的增大而减少;在对称轴右侧,y随x的增大而增大,函数有最小值;②当a<0时,抛物线在对称轴左侧,y随x的增大而增大;在对称轴右侧,y随x的增大而减少,函数有最大值;如果在规定的取值中,要看图象和增减性来判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
