第二章实数同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第二章实数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实数9的算术平方根是( )
A.3 B. C. D.
2.下列说法正确的是( )
A.用计算器进行计算时,其按键顺序如下:,则输出的结果为
B.计算器上先输入某数,再依次按键显示的结果是,则原来输入的某数是
C.用计算器求一组数据的平均数,其按键顺序如下:,则输出的结果为
D.用计算器进行计算,在输入数据过程中,如果发现刚输入的数据有错误,可按键清除最后一步,再重新输入正确数据
3.4的算术平方根是( )
A. B. C.2 D.
4.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为2﹣6,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
5.设边长为的正方形的面积为2.下列关于的四种结论:①是2的算术平方根;②是无理数;③可以用数轴上的一个点来表示;④是无限小数.其中正确结论是( )
A.①②③④ B.①② C.①③ D.②③④
6.下列实数是无理数的是( )
A. B. C. D.
7.一个正方形的面积是3,则这个正方形的边长是( )
A.3 B. C. D.
8.下列实数中,的倒数是( )
A. B. C. D.
9.64的算术平方根是( )
A.4 B. C.8 D.
10.一个正方形的面积是31,估计它的边长大小应该在( ).
A.5与5.5之间 B.5.5与6之间 C.6与6.5之间 D.6.5与7之间
11.有一个数值转换器,原理如图所示,当输入的的值为时,输出的的值是( )
A. B. C. D.
12.下列各数中,是无理数的是( )
A. B. C. D.3.14
二、填空题
13.我们知道,同底数幂的乘法法则为:(其中为正整数),类似地我们规定关于任意正整数的一种新运算:,若,那么 (用含和的代数式表示,其中为正整数).
14.若与是同一个正数的平方根,则a的值为 .
15.如图所示,数轴上表示所对应的点分别为,,点关于点的对称点为,那么点所表示的数是 .
16.将数据6.9401用四舍五入法精确到百分位是 .
17.比较大小: 6.(填“”“”或“”)
三、解答题
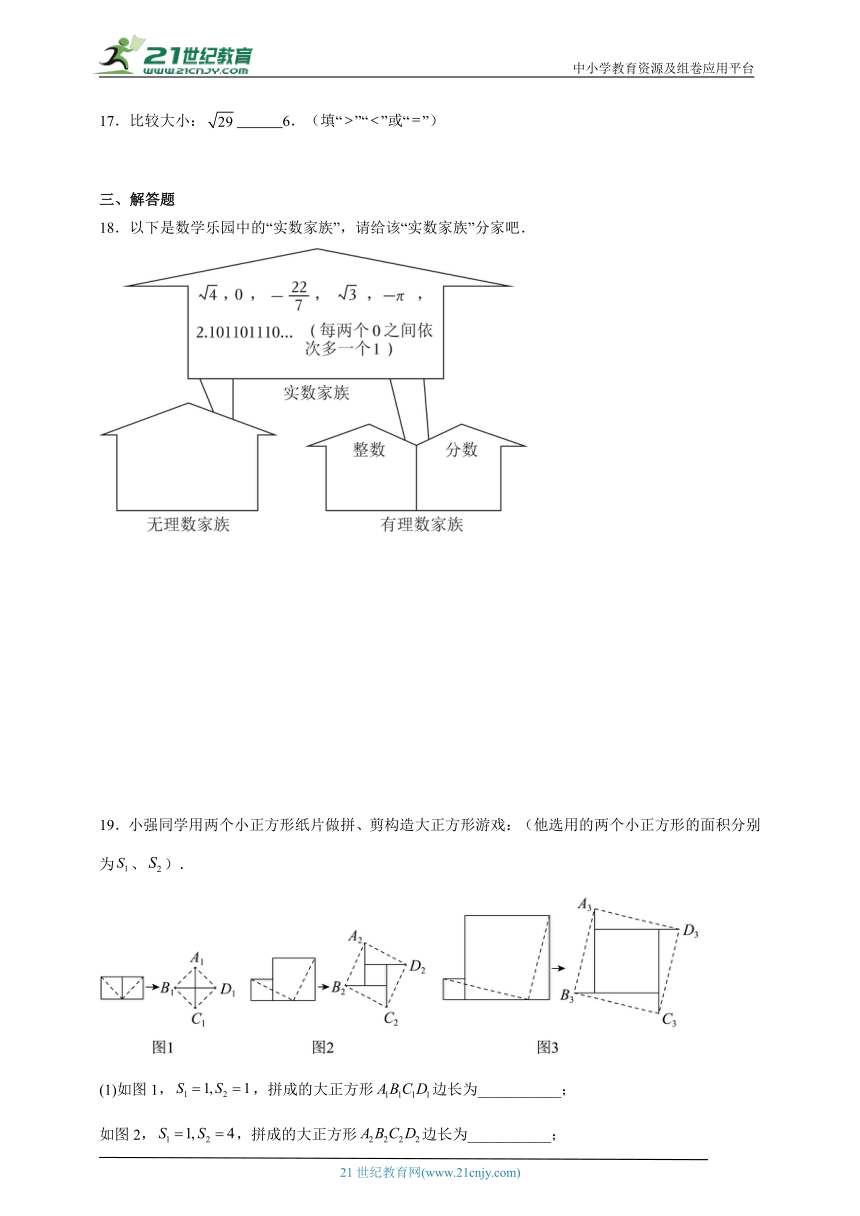
18.以下是数学乐园中的“实数家族”,请给该“实数家族”分家吧.
19.小强同学用两个小正方形纸片做拼、剪构造大正方形游戏:(他选用的两个小正方形的面积分别为、).
(1)如图1,,拼成的大正方形边长为___________;
如图2,,拼成的大正方形边长为___________;
如图3,,拼成的大正方形边长为___________.
(2)若将(1)中的图3沿正方形边的方向剪裁,能否剪出一个面积为14.52且长宽之比为4∶3的长方形?若能,求它的长、宽;若不能,请说明理由;
20.已知的平方根是,的立方根是3,求的平方根.
21.用“作差法”比较和2的大小:,∵,∴,∴,∴.
(1)归纳总结:已知两个数a、b,若,则________0;若,则________0;(填>,<或=)
(2)举一反三:比较与的大小.
22.一个正数的两个平方根分别是与,求和的值.
23.全球气候变暖导致一些冰川融化并消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上生长.每一个苔藓都会长成近似圆形,苔藓的直径和冰川消失后经过的时间近似地满足如下的关系式:d=7×(t≥12).其中d代表苔藓的直径,单位是厘米;t代表冰川消失后经过的时间,单位是年.
(1)计算冰川消失16年后苔藓的直径;
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
24.在数轴上表示下列各数,并将这些数按从小到大的顺序用“<”连接起来.
,,0,,.
《第二章实数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A D C D C B
题号 11 12
答案 D B
1.A
【分析】根据算术平方根的定义即可求出结果.
【详解】解:,
故选:A.
【点睛】本题考查了平方根和算术平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.B
【分析】运用计算器进行验证计算即可.
【详解】解:、计算器求三角函数值时,后面少按了“”,故A不正确;
B、按选项所给的按键顺序可以求出原来输入的数,故B正确;
C、按键中多了“,”,故C不正确;
D、清除刚输入错的数据时,按“”键,故D不正确.
故选:B.
【点睛】本题考查计算器的使用,正确使用计算器是解题的关键.
3.C
【分析】根据算术平方根的性质求解即可.
【详解】4的算术平方根是2.
故选:C.
【点睛】此题主要考查求一个数的算术平方根,熟练掌握算术平方根的性质是解题关键.
4.B
【分析】根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【详解】∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为2﹣6,
∴一个空白长方形面积=,
∵大正方形面积为12,重叠部分面积为3,
∴大正方形边长=,重叠部分边长=,
∴空白部分的长=,
设空白部分宽为x,可得:,解得:x=,
∴小正方形的边长=空白部分的宽+阴影部分边长=,
∴小正方形面积==10,
故选:B.
【点睛】本题主要考查了二次根式的应用,观察图形得到各个正方形边长之间的关系是解题的关键.
5.A
【分析】本题主要考查了无理数的定义,算术平方根,实数与数轴.正确得出a的值是解题的关键.
【详解】解:∵边长为的正方形的面积为2,
∴,
①是2的算术平方根,故此说法正确;
②是无理数,故此说法正确;
③可以用数轴上的一个点来表示,故此说法正确;
④是无限小数,故此说法正确;
综上分析可知,正确结论是①②③④.
故选:A.
6.D
【分析】无理数即为无限不循环小数,初中阶段接触的无理数的表现形式主要有:①开方开不尽的数;②含有的数;③(每两个之间依次多个)这样的数;据此解答即可.
【详解】解:A、,属于整数,不是无理数,不符合题意;
B、为分数,不是无理数,不符合题意;
C、为有限小数,不是无理数,不符合题意;
D、是开方开不尽的数,属于无理数,符合题意;
故选:D.
【点睛】本题考查了无理数的定义以及求一个数的立方根,熟练掌握初中阶段无理数的主要表现形式是解本题的关键.
7.C
【分析】本题考查的是算术平方根的应用,由正方形的面积直接表示正方形的边长即可.
【详解】解:∵一个正方形的面积是3,
∴这个正方形的边长是,
故选:C.
8.D
【分析】根据倒数的定义求解.
【详解】解:,
的倒数是,
故选D.
【点睛】本题考查求一个数的倒数,解题的关键是掌握互为倒数的两个数乘积为1.
9.C
【分析】本题主要考查了算术平方根定义,根据算术平方根定义进行求解即可.
【详解】解:64的算术平方根是8.
故选:C.
10.B
【分析】设正方形的边长为,可得;估算算术平方根的取值范围即可.
【详解】解:设正方形的边长为,则
解得:
∵,且
∴
即
故选:B
【点睛】本题考查估计算术平方根的取值范围.注意计算的准确性.
11.D
【分析】本题考查了立方根,解答此类题目的关键是弄清题目中所给的运算程序.把﹣512按给出的程序逐步计算即可.
【详解】解:由题中所给的程序可知:把取立方根,结果为,
是有理数,
再取立方根为,
是有理数,
再取立方根为,
是无理数,
输出.
故选:D.
12.B
【分析】此题主要考查了无理数的定义,
根据无理数的定义(无理数是指无限不循环小数)进行判断即可.
【详解】解:A、不是无理数,是有理数,故本选项错误;
B、是无理数,故本选项正确;
C、,是有理数,不是无理数,故本选项错误;
D、3.14不是无理数,故本选项错误;
故选:B.
13.
【分析】根据题中的新定义化简,计算即可求出值.
【详解】解:由,
得:原式,
故答案为:.
【点睛】本题考查同底数幂乘法、新定义,解答本题的关键是明确题意,利用新运算求出所求式子的值.
14.1或5
【分析】本题考查平方根,相反数,一元一次方程等知识,是重要考点,掌握相关知识是解题关键.一个正数的平方根是两个互为相反数的式,或两式相等.
【详解】解:∵与是同一个正数的平方根,则两式互为相反数或两式相等,
或,
或,
故答案为:1或5.
15./
【分析】本题主要考查了实数和数轴,数轴上两点间的距离,熟练掌握两点间的距离公式是解题的关键.
根据数轴上两点间的距离公式得到,,,计算即可得到答案.
【详解】解:由题意可得:,,
点对应的数为,
故答案为:.
16.
【分析】精确到百分位,即保留小数点后面第二位,看小数点后面第三位(千分位)上的数字0进行“四舍五入”法解答即可.
【详解】解:6.9401用四舍五入法精确到百分位是6.94.
故答案为:6.94.
【点睛】本题主要考查小数的近似数取值,关键要看清精确到的位数.
17.
【分析】本题考查的是实数的大小比较.根据无理数的估算方法解答即可.
【详解】解:∵,
∴,
故答案为:.
18.无理数家族:,,2.101101110…;
整数:,0,
分数:.
【分析】本题考查实数的分类,根据实数分为无理数和有理数,有理数分为整数和分数,进行作答即可。
【详解】解:,
无理数家族:,,2.101101110…;
有理数家族:,0,;
整数:,0,
分数:.
19.(1);;
(2)不能用正方形纸片裁出符合要求的长方形纸片,理由见解析
【分析】(1)求出所拼成的正方形的面积,再根据算术平方根的定义进行计算即可;
(2)根据题意求出其长、宽,再根据算术平方根进行验证即可.
【详解】(1)解:如图1,当S1=1,S2=1,拼成的大正方形A1B1C1D1的面积为1+1=2,因此其边长为;
如图2,当S1=1,S2=4,拼成的大正方形A2B2C2D2的面积为1+4=5,因此其边长为;
如图3,当S1=1,S2=16,拼成的大正方形A3B3C3D3的面积为1+16=17,因此其边长为;
故答案为:,,;
(2)解:不能,理由如下:
设长方形的长为4x,宽为3x,则有4x 3x=14.52,
所以x2=1.21,
即x=1.1(x>0),
因此长方形的长为4x=4.4,宽为3x=3.3,
因为(4.4)2=19.36>17,
所以不能用正方形A3B3C3D3剪出一个面积为14.52且长宽之比为4:3的长方形.
【点睛】本题考查算术平方根,理解算术平方根的定义是正确解答的前提.
20.
【分析】本题考查平方根、立方根的定义,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.根据平方根、立方根的含义先求解,,再进一步求解即可.
【详解】解:∵的平方根是,的立方根是3,
∴,,
∴,,
∴,
∴的平方根为;
21.(1),
(2)
【分析】此题考查了实数大小比较,关键是熟练掌握作差法.
(1)根据不等式的性质可解答①③,根据等式的性质可解答②;
(2)根据作差法即可比较大小.
【详解】(1)解:①若,则;
②若,则;
③若,则.
故答案为:①,②;
(2)解:
,
,
,
,
.
22.,
【分析】本题考查了平方根的性质,由平方根的性质得,即可求解;理解一个正数的两个平方根互为相反数是解题的关键.
【详解】解:由题意,
得,
解得,
,
23.(1)14cm;
(2)冰川消失16年后苔藓的直径为14cm,冰川约是在37年前消失的.
【详解】试题分析:
(1)把t=16代入计算即可;
(2)把d=35代入解得t即可.
试题解析:
(1)当t=16时,(cm);
答:冰川消失16年后苔藓的直径为14厘米.
(2)当d=35时,,即t-12=25,解得t=37.
答:如果测得一些苔藓的直径是35厘米,冰川约是在37年前消失的.
24.,见解析
【分析】把实数所对应的点画到数轴上,根据数轴上左边的数小于右边的数,进行排序,即可.
【详解】解:,如下图,
.
【点睛】本题考查了立方根、算术平方根、实数的大小比较,实数与数轴,解题的关键是能正确在数轴上表示出各个数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章实数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.实数9的算术平方根是( )
A.3 B. C. D.
2.下列说法正确的是( )
A.用计算器进行计算时,其按键顺序如下:,则输出的结果为
B.计算器上先输入某数,再依次按键显示的结果是,则原来输入的某数是
C.用计算器求一组数据的平均数,其按键顺序如下:,则输出的结果为
D.用计算器进行计算,在输入数据过程中,如果发现刚输入的数据有错误,可按键清除最后一步,再重新输入正确数据
3.4的算术平方根是( )
A. B. C.2 D.
4.在一个正方形的内部按照如图方式放置大小不同的两个小正方形,其中较大的正方形面积为12,重叠部分的面积为3,空白部分的面积为2﹣6,则较小的正方形面积为( )
A.11 B.10 C.9 D.8
5.设边长为的正方形的面积为2.下列关于的四种结论:①是2的算术平方根;②是无理数;③可以用数轴上的一个点来表示;④是无限小数.其中正确结论是( )
A.①②③④ B.①② C.①③ D.②③④
6.下列实数是无理数的是( )
A. B. C. D.
7.一个正方形的面积是3,则这个正方形的边长是( )
A.3 B. C. D.
8.下列实数中,的倒数是( )
A. B. C. D.
9.64的算术平方根是( )
A.4 B. C.8 D.
10.一个正方形的面积是31,估计它的边长大小应该在( ).
A.5与5.5之间 B.5.5与6之间 C.6与6.5之间 D.6.5与7之间
11.有一个数值转换器,原理如图所示,当输入的的值为时,输出的的值是( )
A. B. C. D.
12.下列各数中,是无理数的是( )
A. B. C. D.3.14
二、填空题
13.我们知道,同底数幂的乘法法则为:(其中为正整数),类似地我们规定关于任意正整数的一种新运算:,若,那么 (用含和的代数式表示,其中为正整数).
14.若与是同一个正数的平方根,则a的值为 .
15.如图所示,数轴上表示所对应的点分别为,,点关于点的对称点为,那么点所表示的数是 .
16.将数据6.9401用四舍五入法精确到百分位是 .
17.比较大小: 6.(填“”“”或“”)
三、解答题
18.以下是数学乐园中的“实数家族”,请给该“实数家族”分家吧.
19.小强同学用两个小正方形纸片做拼、剪构造大正方形游戏:(他选用的两个小正方形的面积分别为、).
(1)如图1,,拼成的大正方形边长为___________;
如图2,,拼成的大正方形边长为___________;
如图3,,拼成的大正方形边长为___________.
(2)若将(1)中的图3沿正方形边的方向剪裁,能否剪出一个面积为14.52且长宽之比为4∶3的长方形?若能,求它的长、宽;若不能,请说明理由;
20.已知的平方根是,的立方根是3,求的平方根.
21.用“作差法”比较和2的大小:,∵,∴,∴,∴.
(1)归纳总结:已知两个数a、b,若,则________0;若,则________0;(填>,<或=)
(2)举一反三:比较与的大小.
22.一个正数的两个平方根分别是与,求和的值.
23.全球气候变暖导致一些冰川融化并消失.在冰川消失12年后,一种低等植物苔藓就开始在岩石上生长.每一个苔藓都会长成近似圆形,苔藓的直径和冰川消失后经过的时间近似地满足如下的关系式:d=7×(t≥12).其中d代表苔藓的直径,单位是厘米;t代表冰川消失后经过的时间,单位是年.
(1)计算冰川消失16年后苔藓的直径;
(2)如果测得一些苔藓的直径是35厘米,问冰川约是在多少年前消失的?
24.在数轴上表示下列各数,并将这些数按从小到大的顺序用“<”连接起来.
,,0,,.
《第二章实数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B A D C D C B
题号 11 12
答案 D B
1.A
【分析】根据算术平方根的定义即可求出结果.
【详解】解:,
故选:A.
【点睛】本题考查了平方根和算术平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
2.B
【分析】运用计算器进行验证计算即可.
【详解】解:、计算器求三角函数值时,后面少按了“”,故A不正确;
B、按选项所给的按键顺序可以求出原来输入的数,故B正确;
C、按键中多了“,”,故C不正确;
D、清除刚输入错的数据时,按“”键,故D不正确.
故选:B.
【点睛】本题考查计算器的使用,正确使用计算器是解题的关键.
3.C
【分析】根据算术平方根的性质求解即可.
【详解】4的算术平方根是2.
故选:C.
【点睛】此题主要考查求一个数的算术平方根,熟练掌握算术平方根的性质是解题关键.
4.B
【分析】根据面积可求得大正方形和阴影部分的边长,从而求得空白部分的长;观察可知两块空白部分全等,则可得到一块空白的面积;通过长方形面积公式渴求空白部分的宽,最后求出小正方形的边长即可求出面积.
【详解】∵观察可知,两个空白部分的长相等,宽也相等,
∴重叠部分也为正方形,
∵空白部分的面积为2﹣6,
∴一个空白长方形面积=,
∵大正方形面积为12,重叠部分面积为3,
∴大正方形边长=,重叠部分边长=,
∴空白部分的长=,
设空白部分宽为x,可得:,解得:x=,
∴小正方形的边长=空白部分的宽+阴影部分边长=,
∴小正方形面积==10,
故选:B.
【点睛】本题主要考查了二次根式的应用,观察图形得到各个正方形边长之间的关系是解题的关键.
5.A
【分析】本题主要考查了无理数的定义,算术平方根,实数与数轴.正确得出a的值是解题的关键.
【详解】解:∵边长为的正方形的面积为2,
∴,
①是2的算术平方根,故此说法正确;
②是无理数,故此说法正确;
③可以用数轴上的一个点来表示,故此说法正确;
④是无限小数,故此说法正确;
综上分析可知,正确结论是①②③④.
故选:A.
6.D
【分析】无理数即为无限不循环小数,初中阶段接触的无理数的表现形式主要有:①开方开不尽的数;②含有的数;③(每两个之间依次多个)这样的数;据此解答即可.
【详解】解:A、,属于整数,不是无理数,不符合题意;
B、为分数,不是无理数,不符合题意;
C、为有限小数,不是无理数,不符合题意;
D、是开方开不尽的数,属于无理数,符合题意;
故选:D.
【点睛】本题考查了无理数的定义以及求一个数的立方根,熟练掌握初中阶段无理数的主要表现形式是解本题的关键.
7.C
【分析】本题考查的是算术平方根的应用,由正方形的面积直接表示正方形的边长即可.
【详解】解:∵一个正方形的面积是3,
∴这个正方形的边长是,
故选:C.
8.D
【分析】根据倒数的定义求解.
【详解】解:,
的倒数是,
故选D.
【点睛】本题考查求一个数的倒数,解题的关键是掌握互为倒数的两个数乘积为1.
9.C
【分析】本题主要考查了算术平方根定义,根据算术平方根定义进行求解即可.
【详解】解:64的算术平方根是8.
故选:C.
10.B
【分析】设正方形的边长为,可得;估算算术平方根的取值范围即可.
【详解】解:设正方形的边长为,则
解得:
∵,且
∴
即
故选:B
【点睛】本题考查估计算术平方根的取值范围.注意计算的准确性.
11.D
【分析】本题考查了立方根,解答此类题目的关键是弄清题目中所给的运算程序.把﹣512按给出的程序逐步计算即可.
【详解】解:由题中所给的程序可知:把取立方根,结果为,
是有理数,
再取立方根为,
是有理数,
再取立方根为,
是无理数,
输出.
故选:D.
12.B
【分析】此题主要考查了无理数的定义,
根据无理数的定义(无理数是指无限不循环小数)进行判断即可.
【详解】解:A、不是无理数,是有理数,故本选项错误;
B、是无理数,故本选项正确;
C、,是有理数,不是无理数,故本选项错误;
D、3.14不是无理数,故本选项错误;
故选:B.
13.
【分析】根据题中的新定义化简,计算即可求出值.
【详解】解:由,
得:原式,
故答案为:.
【点睛】本题考查同底数幂乘法、新定义,解答本题的关键是明确题意,利用新运算求出所求式子的值.
14.1或5
【分析】本题考查平方根,相反数,一元一次方程等知识,是重要考点,掌握相关知识是解题关键.一个正数的平方根是两个互为相反数的式,或两式相等.
【详解】解:∵与是同一个正数的平方根,则两式互为相反数或两式相等,
或,
或,
故答案为:1或5.
15./
【分析】本题主要考查了实数和数轴,数轴上两点间的距离,熟练掌握两点间的距离公式是解题的关键.
根据数轴上两点间的距离公式得到,,,计算即可得到答案.
【详解】解:由题意可得:,,
点对应的数为,
故答案为:.
16.
【分析】精确到百分位,即保留小数点后面第二位,看小数点后面第三位(千分位)上的数字0进行“四舍五入”法解答即可.
【详解】解:6.9401用四舍五入法精确到百分位是6.94.
故答案为:6.94.
【点睛】本题主要考查小数的近似数取值,关键要看清精确到的位数.
17.
【分析】本题考查的是实数的大小比较.根据无理数的估算方法解答即可.
【详解】解:∵,
∴,
故答案为:.
18.无理数家族:,,2.101101110…;
整数:,0,
分数:.
【分析】本题考查实数的分类,根据实数分为无理数和有理数,有理数分为整数和分数,进行作答即可。
【详解】解:,
无理数家族:,,2.101101110…;
有理数家族:,0,;
整数:,0,
分数:.
19.(1);;
(2)不能用正方形纸片裁出符合要求的长方形纸片,理由见解析
【分析】(1)求出所拼成的正方形的面积,再根据算术平方根的定义进行计算即可;
(2)根据题意求出其长、宽,再根据算术平方根进行验证即可.
【详解】(1)解:如图1,当S1=1,S2=1,拼成的大正方形A1B1C1D1的面积为1+1=2,因此其边长为;
如图2,当S1=1,S2=4,拼成的大正方形A2B2C2D2的面积为1+4=5,因此其边长为;
如图3,当S1=1,S2=16,拼成的大正方形A3B3C3D3的面积为1+16=17,因此其边长为;
故答案为:,,;
(2)解:不能,理由如下:
设长方形的长为4x,宽为3x,则有4x 3x=14.52,
所以x2=1.21,
即x=1.1(x>0),
因此长方形的长为4x=4.4,宽为3x=3.3,
因为(4.4)2=19.36>17,
所以不能用正方形A3B3C3D3剪出一个面积为14.52且长宽之比为4:3的长方形.
【点睛】本题考查算术平方根,理解算术平方根的定义是正确解答的前提.
20.
【分析】本题考查平方根、立方根的定义,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.根据平方根、立方根的含义先求解,,再进一步求解即可.
【详解】解:∵的平方根是,的立方根是3,
∴,,
∴,,
∴,
∴的平方根为;
21.(1),
(2)
【分析】此题考查了实数大小比较,关键是熟练掌握作差法.
(1)根据不等式的性质可解答①③,根据等式的性质可解答②;
(2)根据作差法即可比较大小.
【详解】(1)解:①若,则;
②若,则;
③若,则.
故答案为:①,②;
(2)解:
,
,
,
,
.
22.,
【分析】本题考查了平方根的性质,由平方根的性质得,即可求解;理解一个正数的两个平方根互为相反数是解题的关键.
【详解】解:由题意,
得,
解得,
,
23.(1)14cm;
(2)冰川消失16年后苔藓的直径为14cm,冰川约是在37年前消失的.
【详解】试题分析:
(1)把t=16代入计算即可;
(2)把d=35代入解得t即可.
试题解析:
(1)当t=16时,(cm);
答:冰川消失16年后苔藓的直径为14厘米.
(2)当d=35时,,即t-12=25,解得t=37.
答:如果测得一些苔藓的直径是35厘米,冰川约是在37年前消失的.
24.,见解析
【分析】把实数所对应的点画到数轴上,根据数轴上左边的数小于右边的数,进行排序,即可.
【详解】解:,如下图,
.
【点睛】本题考查了立方根、算术平方根、实数的大小比较,实数与数轴,解题的关键是能正确在数轴上表示出各个数.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
