第三章一元一次不等式(组)同步练习(含解析)
文档属性
| 名称 | 第三章一元一次不等式(组)同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 737.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三章一元一次不等式(组)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.不等式的解( )
A.为0,1,2 B.为0,1 C.为1,2 D.有无数个
2.某单位对某村庄提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户只;若每户发放母羊只,则多出只母羊;若每户发放母羊只,则有一户可分得母羊但不足只.这批种羊共( )
A.只 B.只 C.只 D.只
3.不等式的解集为( )
A. B. C. D.
4.若方程的解是非负数,则的取值是( )
A. B. C. D.
5.下列说法错误的是( )
A.不等式的整数解有无数个 B.不等式的非负整数解有有限个
C.不等式的解集是 D.是不等式的一个解
6.某品牌亚麻服装进价为200元/件,标价为300元/件,由于搞活动,商店准备打折销售,但要保证利润率不低于,则该品牌亚麻服装每件最多可打( )
A.9折 B.8折 C.7折 D.3.5折
7.若,则下列不等式一定成立的为( )
A. B. C. D.
8.某超市以160元的价格购进某种商品,将进价提高一定百分比后标价出售,并在标价的基础上推出8折优惠活动,若利润率仍不少于,则提高的百分比至少为( )
A. B. C. D.
9.已知,若是任意实数,则下列不等式始终成立的是( )
A. B. C. D.
10.一艘船从某江上游的甲地匀速驶到下游的乙地用了,又从乙地匀速返回甲地用了不超过,船在静水里的平均速度为,江水最大流速为( )
A. B. C. D.
11.已知关于x的不等式无解,则a的取值范围为( )
A.a<2 B.a>2 C.a≤2 D.a≥2
12.不等式的解集在数轴上表示为( )
A. B. C. D.
二、填空题
13.鱼缸里饲养、两种鱼,种鱼的生长温度的范围是,种鱼的生长温度的范围是,那么鱼缸里的温度应该控制在 范围内.
14.“鲁巴好少年,一起向未来”,重庆市鲁能巴蜀中学校春季运动会在4月27日如期举行.各班同学积极参与,热情高涨;运动员挥洒汗水,激昂赛场;场下观众文明观赛,有序加油.后勤团队也不甘示弱,积极为同学们做好各种后勤保障,其中,采购小组的同学们就为全班同学准备了百事可乐,红牛和脉动三种饮料.已知百事可乐、红牛和脉动的单价之和为14元,计划购买百事可乐,红牛和脉动的数量总共不超过160瓶,其中脉动的单价为每瓶5元,计划购买20瓶,百事可乐的数量不多于红牛数量的一半,但至少购买40瓶,结果,在做预算时,将百事可乐和红牛的单价弄反了,结果在实际购买时,总费用比预算多了150元.若百事可乐、红牛和脉动的单价均为整数,则实际购买百事可乐、红牛和脉动的总费用最多需要花费 .
15.已知关于x的不等式的解集是,则m的取值范围是 .
16.对于下列结论:①为正数,则;②为自然数,则;③不大于5,则;正确的有 .(填所有正确的序号)
17.若关于x的不等式组的解集为,则m的取值范围是 .
三、解答题
18.用适当的符号表示下列关系:
(1)x的3倍与x的2倍的和是正数;
(2)一枚炮弹的杀伤半径不小于300米;
(3)三件上衣与四条长裤的总价钱不高于268元;
(4)明天下雨的可能性不小于70%;
(5)小明的体重不比小刚轻.
19.(应用意识)为了交通便捷,某省开始修建高铁,其中段将于2025年年底建成.开通后的段高铁将比现在运行的段城际铁路全长缩短,全程仅需.已知段城际列车全程需要,平均速度是开通后的高铁的.
(1)段高铁与段城际铁路全长各为多少千米?
(2)甲、乙两个工程队同时对段高铁全线某个配套项目进行施工,每天对其施工的长度比为,计划40天完成.施工5天后,工程指挥部要求甲工程队提高工效,以确保整个工程提早3天以上(含3天)完成,那么甲工程队后期每天至少施工多少千米?
20.解下列不等式组, 并写出它的所有整数解.
21.已知,利用不等式的性质比较与的大小.
22.某果蔬加工公司购买龙眼,公司把购买的龙眼加工成桂圆肉和龙眼干,龙眼可加工成桂圆肉或龙眼干,桂圆肉和龙眼干的销售价格分别是10万元和3万元.若全部销售完的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉?
23.为建设美丽郑州,某治污公司决定购买10台污水处理设备.现有,两种型号的设备,其中每台的价格与月处理污水量如下表:
型 型
价格(万元/台)
处理污水量(吨/月) 240 200
经调查:购买一台型设备比购买一台型设备多2万元,购买2台型设备比购买3台型设备少6万元.
(1)求,的值;
(2)如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;
(3)在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.
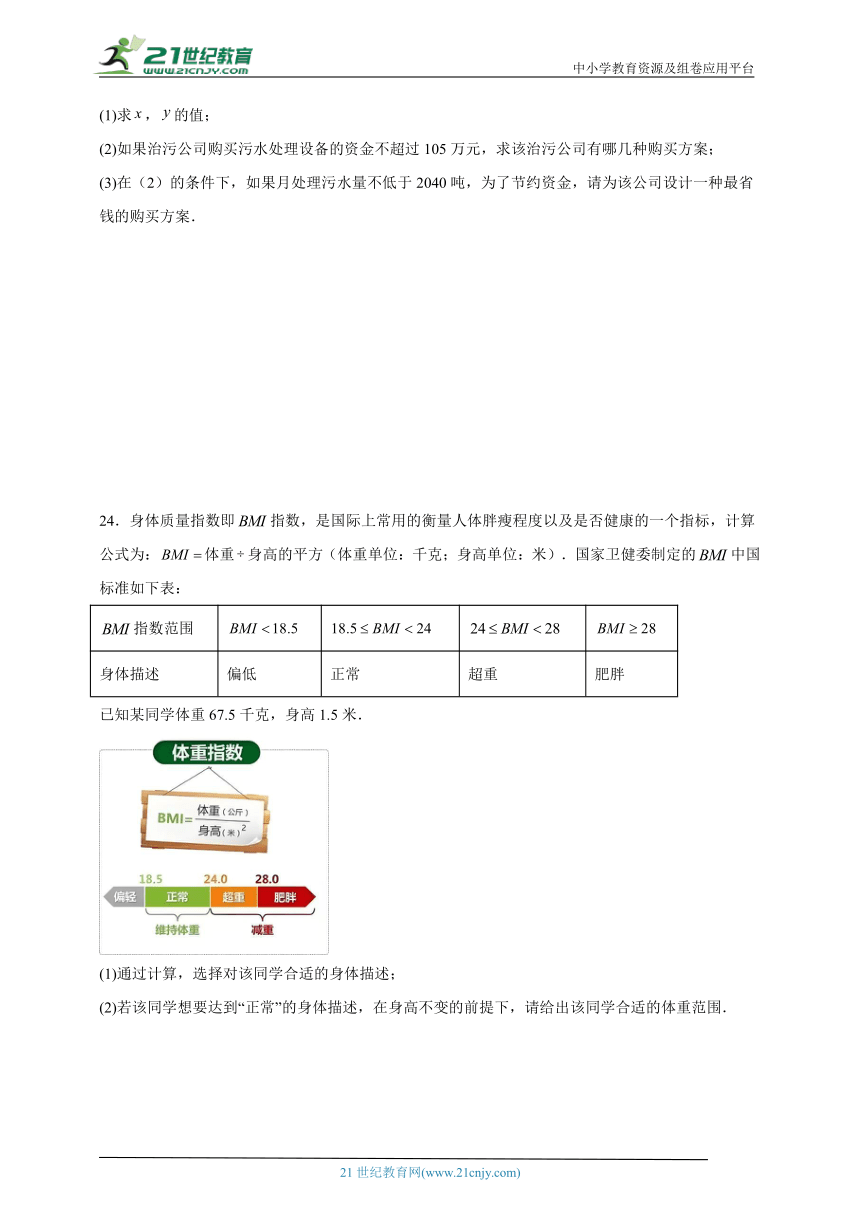
24.身体质量指数即指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个指标,计算公式为:体重身高的平方(体重单位:千克;身高单位:米).国家卫健委制定的中国标准如下表:
指数范围
身体描述 偏低 正常 超重 肥胖
已知某同学体重67.5千克,身高1.5米.
(1)通过计算,选择对该同学合适的身体描述;
(2)若该同学想要达到“正常”的身体描述,在身高不变的前提下,请给出该同学合适的体重范围.
《第三章一元一次不等式(组)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D B C D C B C
题号 11 12
答案 B D
1.D
【分析】根据不等式解的定义求解即可.
【详解】解:∵,
∴满足不等式的解有无数个,
故选D.
【点睛】本题主要考查了不等式的解,熟知不等式解的定义是解题的关键.
2.D
【分析】本题考查了一元一次不等式组的应用,解答本题的关键是理解题意,正确列出一元一次不等式组.
设公羊共只,则母羊共只,根据“若每户发放母羊只,则有一户可分得母羊但不足只”列出一元一次不等式组,解答即可.
【详解】解:设公羊共只,则母羊共只,
根据题意得:,
解得:,
又为正整数,
,
,
这批种羊共只,
故选:D.
3.B
【分析】本题考查了解一元一次不等式,解题的关键是掌握一元一次不等式的解法.根据不等式的性质求出的范围即可.
【详解】解:,
,
,
故选:B.
4.D
【分析】本题考查了解一元一次方程和解一元一次不等式,熟练掌握解方程和不等式的方法是解题的关键.先解一元一次方程,再根据题意构建关于的一元一次不等式,最后解不等式即可.
【详解】解:解方程,可得,
∵该方程的解是非负数,
∴,
解得.
故选:D.
5.B
【分析】本题考查了不等式的解和解一元一次不等式,熟知解一元一次不等式的方法和一元一次不等式解的定义是解题的关键.根据不等式的解和解一元一次不等式的相关概念求解并判断,即可解题.
【详解】解:A、不等式的整数解有无数个,正确,不符合题意;
B、不等式的非负整数解有无限个,选项说法错误,符合题意;
C、不等式的解集是,正确,不符合题意;
D、,
,即是不等式的一个解,正确,不符合题意;
故选:B.
6.C
【分析】本题考查一元一次不等式的应用,设可以打折,根据利润不低于,即可列出一元一次不等式,解不等式即可得出结论.
【详解】解:设可打折,利润率不低于,
根据题意得:,
,
则最多打7折.
故选:C.
7.D
【分析】本题考查了不等式的基本性质,解题的关键是掌握不等式的基本性质.由不等式的基本性质,分别对每个选项进行判断,即可得到答案.
【详解】解:A、,
,故A错误,不符合题意;
B、,
,故B错误,不符合题意;
C、,
当时,,当时,,故C错误,不符合题意;
D、,
,故D正确,符合题意;
故选:D.
8.C
【分析】本题主要考查一元一次不等式的应用,设提高的百分比至少为,根据利润率=(售价-进价)÷进价列不等式求解即可.
【详解】解:提高的百分比至少为,根据题意得,
,
解得,,
即:提高的百分比至少为,
故选:C.
9.B
【分析】本题考查了不等式的性质,根据不等式的性质逐项判断即可求解,掌握不等式的性质是解题的关键.
【详解】解:、∵,
∴,该选项错误,不合题意;
、∵,
∴,该选项正确,符合题意;
、∵,
当时,;当时,;当时,,该选项错误,不合题意;
、∵,
当时,;当时,;当时,,该选项错误,不合题意;
故选:.
10.C
【分析】设江水的流速是,利用路程=速度×时间,结合从乙地匀速返回甲地用了不超过,可列出关于x的一元一次不等式,解之取其中的最大值,即可得出结论.
【详解】解:设江水的流速是,
根据题意得:,
解得:,
∴x的最大值为3,
即江水最大流速为.
故选:C.
【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
11.B
【分析】先整理不等式组,根据无解的条件列出不等式,求出a的取值范围即可.
【详解】解:整理不等式组得:,
∵不等式组无解,
∴2.
故选:B.
【点睛】本题主要考查了不等式组无解的条件,根据整理出的不等式组和无解的条件列出关于a的不等式是解答本题的关键.
12.D
【分析】本题主要考查了在数轴上表示不等式的解集,先求出不等式的解集,然后在数轴上表示出来即可.
【详解】解:,
解得.
在数轴上表示为:
故选:D.
13./
【分析】本题考查了不等式的取值范围,掌握不等式解集的规律是解题的关键,根据:“同大取大,同小取小,大小小大取中间”,即可求解.
【详解】解:根据题意可得:,
故答案为:.
14.805元
【分析】设购买瓶百事可乐,瓶红牛,百事可乐的单价为元,则红牛的单价为元,根据在做预算时,将百事可乐和红牛的单价弄反了,结果在实际购买时,总费用比预算多了 元,可得,整理得:,再根据百事可乐的数量不多于红牛数量的一半,但至少购买瓶,可得,,,根据x,y,m均为正整数,,可得,可得m=2或m=3或m=4,依此进行讨论即可求解.
【详解】解:设购买x瓶百事可乐,y瓶红牛,百事可乐的单价为m元,则红牛的单价为14﹣5﹣m=(9﹣m)元,
依题意得:xm+y(9﹣m)﹣[x(9﹣m)+ym]=150,
整理得:,
∵,x≥40,
∴x+y+20≤160,
∴x+y≤140,
又∵x,y,m均为正整数,x≤y,
∴y﹣x是正整数,
∵m<4.5,
∴9﹣2m=7(舍去)或9﹣2m=5或9﹣2m=3或9﹣2m=1,
∴m=2或m=3或m=4,
当m=2时,9﹣m=7,y﹣x=30,
∴ ,
解得:40≤x≤55,
此时实际购买这三种物品的总费用为:
5×20+2x+7y=100+2x+7(x+30)=9x+310,
∴当x取最大值55时,总费用最大为9×55+310=805(元)(不合题意舍去);
当m=3时,9﹣m=6,y﹣x=50,
,
解得40≤y≤45,
∴此时实际购买这三种物品的总费用为:
5×20+3x+6(x+50)=9x+400,
∴当x取最大值45时,总费用最大为9×55+40=805(元);
当m=4时,9﹣m=5,y﹣x=150,
∴,
此时不等式组无解.
综上所述,实际购买百事可乐、红牛和脉动的总费用最多需要花费805元.
故答案为:895元.
【点睛】本题考查了应用类问题,不定方程的应用,解题的关键是正确读懂题意列出方程和代数式.
15.
【分析】本题考查了不等式的性质,不等式两边同时除以同一个负数,不等式符号改变,即由的解集是,得出,则可得出答案.
【详解】解:∵
∴,
∵的解集是,
∴不等号的方向已改变,
∴,
故答案为:.
16.①③
【分析】本题考查了不等式的定义,根据正数大于0,自然数是非负整数,不大于即小于或等于,逐项判断即可得解.
【详解】解:①为正数,则,故①说法正确,符合题意;
②为自然数,则,故②说法错误,不符合题意;
③不大于5,则,故③说法正确,符合题意;
综上所述,正确的有①③,
故答案为:①③.
17.
【分析】本题考查根据不等式组的解集求参数的值,熟练掌握“同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集”是解题的关键.
先求出每一个不等式的解集,再根据不等式组的解集,求出m的范围即可.
【详解】解:解不等式,得;
解不等式,得.
不等式组的解集为,
.
故答案为:.
18.(1)3x+2x>0
(2)r≥300
(3)3a+4b≤268
(4)P≥70%
(5)设小明的体重为a千克,小刚的体重为b千克,a≥b
【分析】根据每一道题所叙述内容列出不等关系即可,注意大于与大于等于,小于与小于等于的区别.
【详解】(1)3x+2x>0;
(2)设炮弹的杀伤半径为r米,r≥300;
(3)设每件上衣为a元,每条长裤是b元,3a+4b≤268;
(4)用P表示明天下雨的可能性,P≥70%;
(5)设小明的体重为a千克,小刚的体重为b千克,a≥b.
【点睛】本题考查列不等式,能够分析题意找出不等关系是解决本题的关键.
19.(1)段高铁全长为段城际铁路全长为
(2)甲工程队后期每天至少施工
【分析】本题考查二元一次方程组和一元一次不等式的应用,解题的关键是理解题意,根据等量关系列出方程组,和不等式即可.
(1)设段高铁全长为段城际铁路全长为,由题意得到二元一次方程组,求解即可;
(2)设甲队后期每天施工,甲队原来每天的施工长度为(千米),乙每天的施工长度为(千米),根据题意列出一元一次不等式即可.
【详解】(1)解:设段高铁全长为段城际铁路全长为.
根据题意,得
解得
故段高铁全长为段城际铁路全长为.
(2)解:设甲工程队后期每天施工.
甲工程队原来每天的施工长度为,
乙工程队每天的施工长度为.
根据题意,得,解得.
故甲工程队后期每天至少施工.
20.,整数解为:,,
【分析】本题考查的是求解不等式组的整数解,先分别解不等式组中的两个不等式,再确定解集的公共部分即可得到不等式组的解集,再确定整数解即可.
【详解】解:
由①得:
由②得:
所以不等式组的解为:
∴整数解为: 2,3,4.
21.
【分析】本题考查了不等式的基本性质,根据不等式两边加(或减)同一个数(或式子),不等号的方向不变,不等式两边乘(或除以)同一个负数,不等号的方向改变进行解答即可.
【详解】解:∵,
∴,
∴.
22.至少需要把龙眼加工成桂圆肉
【分析】此题考查了一元一次不等式的应用,明确题意列出一元一次不等式是解答本题的关键.
设把龙眼加工成桂圆肉,则有的龙眼加工成龙眼干,根据题意列出一元一次不等式求解即可.
【详解】解:设把龙眼加工成桂圆肉,则有的龙眼加工成龙眼干.
由题意,得,
解得.
答:至少需要把龙眼加工成桂圆肉.
23.(1)
(2)三种购买方案:型设备0台,型设备10台;型设备1台,型设备9台;型设备2台,型设备8台;
(3)购买型设备1台,型设备9台最省钱
【分析】(1)根据题意列出关于x、y的二元一次方程组,然后解方程即可;
(2)设购买型设备a台,则购买型设备台,根据题意列出关于a的不等式,然后解不等式,根据a为整数可求解;
(3)根据题意和(2)中所求得到或2,然后分别求得购买费用,比较大小即可.
【详解】(1)解:由题意,,
∴;
(2)解:设购买型设备a台,则购买型设备台,
根据题意,得且,
解得,又a为整数,
∴该治污公司有三种购买方案:型设备0台,型设备10台;型设备1台,型设备9台;型设备2台,型设备8台;
(3)解:由题意得,解得,
∴或2,
当时,买设备的费用为(元),
当时,买设备的费用为(元),
∵,
∴购买型设备1台,型设备9台最省钱.
【点睛】本题考查一元一次不等式的应用、二元一次方程组的应用,理解题意,找到题中等量和不等量关系并正确求解是解答的关键.
24.(1)该同学的身体描述为肥胖
(2)
【分析】本题考查了不等式的应用.
(1)先根据计算公式计算出,再根据表格得出结论即可;
(2)设在身高1.5米的前提下,设体重x千克后身体达到正常,根据题意列出不等式,解不等式即可.
【详解】(1)解:∵体重67.5千克,身高1.5米,
∴,
∴该同学的身体描述为肥胖;
(2)解:设在身高1.5米的前提下,设体重x千克后身体达到正常,
则,
∴解得,
∴该同学应该减轻体重的范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章一元一次不等式(组)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.不等式的解( )
A.为0,1,2 B.为0,1 C.为1,2 D.有无数个
2.某单位对某村庄提供优质种羊若干只.在准备配发的过程中发现:公羊刚好每户只;若每户发放母羊只,则多出只母羊;若每户发放母羊只,则有一户可分得母羊但不足只.这批种羊共( )
A.只 B.只 C.只 D.只
3.不等式的解集为( )
A. B. C. D.
4.若方程的解是非负数,则的取值是( )
A. B. C. D.
5.下列说法错误的是( )
A.不等式的整数解有无数个 B.不等式的非负整数解有有限个
C.不等式的解集是 D.是不等式的一个解
6.某品牌亚麻服装进价为200元/件,标价为300元/件,由于搞活动,商店准备打折销售,但要保证利润率不低于,则该品牌亚麻服装每件最多可打( )
A.9折 B.8折 C.7折 D.3.5折
7.若,则下列不等式一定成立的为( )
A. B. C. D.
8.某超市以160元的价格购进某种商品,将进价提高一定百分比后标价出售,并在标价的基础上推出8折优惠活动,若利润率仍不少于,则提高的百分比至少为( )
A. B. C. D.
9.已知,若是任意实数,则下列不等式始终成立的是( )
A. B. C. D.
10.一艘船从某江上游的甲地匀速驶到下游的乙地用了,又从乙地匀速返回甲地用了不超过,船在静水里的平均速度为,江水最大流速为( )
A. B. C. D.
11.已知关于x的不等式无解,则a的取值范围为( )
A.a<2 B.a>2 C.a≤2 D.a≥2
12.不等式的解集在数轴上表示为( )
A. B. C. D.
二、填空题
13.鱼缸里饲养、两种鱼,种鱼的生长温度的范围是,种鱼的生长温度的范围是,那么鱼缸里的温度应该控制在 范围内.
14.“鲁巴好少年,一起向未来”,重庆市鲁能巴蜀中学校春季运动会在4月27日如期举行.各班同学积极参与,热情高涨;运动员挥洒汗水,激昂赛场;场下观众文明观赛,有序加油.后勤团队也不甘示弱,积极为同学们做好各种后勤保障,其中,采购小组的同学们就为全班同学准备了百事可乐,红牛和脉动三种饮料.已知百事可乐、红牛和脉动的单价之和为14元,计划购买百事可乐,红牛和脉动的数量总共不超过160瓶,其中脉动的单价为每瓶5元,计划购买20瓶,百事可乐的数量不多于红牛数量的一半,但至少购买40瓶,结果,在做预算时,将百事可乐和红牛的单价弄反了,结果在实际购买时,总费用比预算多了150元.若百事可乐、红牛和脉动的单价均为整数,则实际购买百事可乐、红牛和脉动的总费用最多需要花费 .
15.已知关于x的不等式的解集是,则m的取值范围是 .
16.对于下列结论:①为正数,则;②为自然数,则;③不大于5,则;正确的有 .(填所有正确的序号)
17.若关于x的不等式组的解集为,则m的取值范围是 .
三、解答题
18.用适当的符号表示下列关系:
(1)x的3倍与x的2倍的和是正数;
(2)一枚炮弹的杀伤半径不小于300米;
(3)三件上衣与四条长裤的总价钱不高于268元;
(4)明天下雨的可能性不小于70%;
(5)小明的体重不比小刚轻.
19.(应用意识)为了交通便捷,某省开始修建高铁,其中段将于2025年年底建成.开通后的段高铁将比现在运行的段城际铁路全长缩短,全程仅需.已知段城际列车全程需要,平均速度是开通后的高铁的.
(1)段高铁与段城际铁路全长各为多少千米?
(2)甲、乙两个工程队同时对段高铁全线某个配套项目进行施工,每天对其施工的长度比为,计划40天完成.施工5天后,工程指挥部要求甲工程队提高工效,以确保整个工程提早3天以上(含3天)完成,那么甲工程队后期每天至少施工多少千米?
20.解下列不等式组, 并写出它的所有整数解.
21.已知,利用不等式的性质比较与的大小.
22.某果蔬加工公司购买龙眼,公司把购买的龙眼加工成桂圆肉和龙眼干,龙眼可加工成桂圆肉或龙眼干,桂圆肉和龙眼干的销售价格分别是10万元和3万元.若全部销售完的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉?
23.为建设美丽郑州,某治污公司决定购买10台污水处理设备.现有,两种型号的设备,其中每台的价格与月处理污水量如下表:
型 型
价格(万元/台)
处理污水量(吨/月) 240 200
经调查:购买一台型设备比购买一台型设备多2万元,购买2台型设备比购买3台型设备少6万元.
(1)求,的值;
(2)如果治污公司购买污水处理设备的资金不超过105万元,求该治污公司有哪几种购买方案;
(3)在(2)的条件下,如果月处理污水量不低于2040吨,为了节约资金,请为该公司设计一种最省钱的购买方案.
24.身体质量指数即指数,是国际上常用的衡量人体胖瘦程度以及是否健康的一个指标,计算公式为:体重身高的平方(体重单位:千克;身高单位:米).国家卫健委制定的中国标准如下表:
指数范围
身体描述 偏低 正常 超重 肥胖
已知某同学体重67.5千克,身高1.5米.
(1)通过计算,选择对该同学合适的身体描述;
(2)若该同学想要达到“正常”的身体描述,在身高不变的前提下,请给出该同学合适的体重范围.
《第三章一元一次不等式(组)》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D B D B C D C B C
题号 11 12
答案 B D
1.D
【分析】根据不等式解的定义求解即可.
【详解】解:∵,
∴满足不等式的解有无数个,
故选D.
【点睛】本题主要考查了不等式的解,熟知不等式解的定义是解题的关键.
2.D
【分析】本题考查了一元一次不等式组的应用,解答本题的关键是理解题意,正确列出一元一次不等式组.
设公羊共只,则母羊共只,根据“若每户发放母羊只,则有一户可分得母羊但不足只”列出一元一次不等式组,解答即可.
【详解】解:设公羊共只,则母羊共只,
根据题意得:,
解得:,
又为正整数,
,
,
这批种羊共只,
故选:D.
3.B
【分析】本题考查了解一元一次不等式,解题的关键是掌握一元一次不等式的解法.根据不等式的性质求出的范围即可.
【详解】解:,
,
,
故选:B.
4.D
【分析】本题考查了解一元一次方程和解一元一次不等式,熟练掌握解方程和不等式的方法是解题的关键.先解一元一次方程,再根据题意构建关于的一元一次不等式,最后解不等式即可.
【详解】解:解方程,可得,
∵该方程的解是非负数,
∴,
解得.
故选:D.
5.B
【分析】本题考查了不等式的解和解一元一次不等式,熟知解一元一次不等式的方法和一元一次不等式解的定义是解题的关键.根据不等式的解和解一元一次不等式的相关概念求解并判断,即可解题.
【详解】解:A、不等式的整数解有无数个,正确,不符合题意;
B、不等式的非负整数解有无限个,选项说法错误,符合题意;
C、不等式的解集是,正确,不符合题意;
D、,
,即是不等式的一个解,正确,不符合题意;
故选:B.
6.C
【分析】本题考查一元一次不等式的应用,设可以打折,根据利润不低于,即可列出一元一次不等式,解不等式即可得出结论.
【详解】解:设可打折,利润率不低于,
根据题意得:,
,
则最多打7折.
故选:C.
7.D
【分析】本题考查了不等式的基本性质,解题的关键是掌握不等式的基本性质.由不等式的基本性质,分别对每个选项进行判断,即可得到答案.
【详解】解:A、,
,故A错误,不符合题意;
B、,
,故B错误,不符合题意;
C、,
当时,,当时,,故C错误,不符合题意;
D、,
,故D正确,符合题意;
故选:D.
8.C
【分析】本题主要考查一元一次不等式的应用,设提高的百分比至少为,根据利润率=(售价-进价)÷进价列不等式求解即可.
【详解】解:提高的百分比至少为,根据题意得,
,
解得,,
即:提高的百分比至少为,
故选:C.
9.B
【分析】本题考查了不等式的性质,根据不等式的性质逐项判断即可求解,掌握不等式的性质是解题的关键.
【详解】解:、∵,
∴,该选项错误,不合题意;
、∵,
∴,该选项正确,符合题意;
、∵,
当时,;当时,;当时,,该选项错误,不合题意;
、∵,
当时,;当时,;当时,,该选项错误,不合题意;
故选:.
10.C
【分析】设江水的流速是,利用路程=速度×时间,结合从乙地匀速返回甲地用了不超过,可列出关于x的一元一次不等式,解之取其中的最大值,即可得出结论.
【详解】解:设江水的流速是,
根据题意得:,
解得:,
∴x的最大值为3,
即江水最大流速为.
故选:C.
【点睛】本题考查了一元一次不等式的应用,根据各数量之间的关系,正确列出一元一次不等式是解题的关键.
11.B
【分析】先整理不等式组,根据无解的条件列出不等式,求出a的取值范围即可.
【详解】解:整理不等式组得:,
∵不等式组无解,
∴
故选:B.
【点睛】本题主要考查了不等式组无解的条件,根据整理出的不等式组和无解的条件列出关于a的不等式是解答本题的关键.
12.D
【分析】本题主要考查了在数轴上表示不等式的解集,先求出不等式的解集,然后在数轴上表示出来即可.
【详解】解:,
解得.
在数轴上表示为:
故选:D.
13./
【分析】本题考查了不等式的取值范围,掌握不等式解集的规律是解题的关键,根据:“同大取大,同小取小,大小小大取中间”,即可求解.
【详解】解:根据题意可得:,
故答案为:.
14.805元
【分析】设购买瓶百事可乐,瓶红牛,百事可乐的单价为元,则红牛的单价为元,根据在做预算时,将百事可乐和红牛的单价弄反了,结果在实际购买时,总费用比预算多了 元,可得,整理得:,再根据百事可乐的数量不多于红牛数量的一半,但至少购买瓶,可得,,,根据x,y,m均为正整数,,可得,可得m=2或m=3或m=4,依此进行讨论即可求解.
【详解】解:设购买x瓶百事可乐,y瓶红牛,百事可乐的单价为m元,则红牛的单价为14﹣5﹣m=(9﹣m)元,
依题意得:xm+y(9﹣m)﹣[x(9﹣m)+ym]=150,
整理得:,
∵,x≥40,
∴x+y+20≤160,
∴x+y≤140,
又∵x,y,m均为正整数,x≤y,
∴y﹣x是正整数,
∵m<4.5,
∴9﹣2m=7(舍去)或9﹣2m=5或9﹣2m=3或9﹣2m=1,
∴m=2或m=3或m=4,
当m=2时,9﹣m=7,y﹣x=30,
∴ ,
解得:40≤x≤55,
此时实际购买这三种物品的总费用为:
5×20+2x+7y=100+2x+7(x+30)=9x+310,
∴当x取最大值55时,总费用最大为9×55+310=805(元)(不合题意舍去);
当m=3时,9﹣m=6,y﹣x=50,
,
解得40≤y≤45,
∴此时实际购买这三种物品的总费用为:
5×20+3x+6(x+50)=9x+400,
∴当x取最大值45时,总费用最大为9×55+40=805(元);
当m=4时,9﹣m=5,y﹣x=150,
∴,
此时不等式组无解.
综上所述,实际购买百事可乐、红牛和脉动的总费用最多需要花费805元.
故答案为:895元.
【点睛】本题考查了应用类问题,不定方程的应用,解题的关键是正确读懂题意列出方程和代数式.
15.
【分析】本题考查了不等式的性质,不等式两边同时除以同一个负数,不等式符号改变,即由的解集是,得出,则可得出答案.
【详解】解:∵
∴,
∵的解集是,
∴不等号的方向已改变,
∴,
故答案为:.
16.①③
【分析】本题考查了不等式的定义,根据正数大于0,自然数是非负整数,不大于即小于或等于,逐项判断即可得解.
【详解】解:①为正数,则,故①说法正确,符合题意;
②为自然数,则,故②说法错误,不符合题意;
③不大于5,则,故③说法正确,符合题意;
综上所述,正确的有①③,
故答案为:①③.
17.
【分析】本题考查根据不等式组的解集求参数的值,熟练掌握“同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集”是解题的关键.
先求出每一个不等式的解集,再根据不等式组的解集,求出m的范围即可.
【详解】解:解不等式,得;
解不等式,得.
不等式组的解集为,
.
故答案为:.
18.(1)3x+2x>0
(2)r≥300
(3)3a+4b≤268
(4)P≥70%
(5)设小明的体重为a千克,小刚的体重为b千克,a≥b
【分析】根据每一道题所叙述内容列出不等关系即可,注意大于与大于等于,小于与小于等于的区别.
【详解】(1)3x+2x>0;
(2)设炮弹的杀伤半径为r米,r≥300;
(3)设每件上衣为a元,每条长裤是b元,3a+4b≤268;
(4)用P表示明天下雨的可能性,P≥70%;
(5)设小明的体重为a千克,小刚的体重为b千克,a≥b.
【点睛】本题考查列不等式,能够分析题意找出不等关系是解决本题的关键.
19.(1)段高铁全长为段城际铁路全长为
(2)甲工程队后期每天至少施工
【分析】本题考查二元一次方程组和一元一次不等式的应用,解题的关键是理解题意,根据等量关系列出方程组,和不等式即可.
(1)设段高铁全长为段城际铁路全长为,由题意得到二元一次方程组,求解即可;
(2)设甲队后期每天施工,甲队原来每天的施工长度为(千米),乙每天的施工长度为(千米),根据题意列出一元一次不等式即可.
【详解】(1)解:设段高铁全长为段城际铁路全长为.
根据题意,得
解得
故段高铁全长为段城际铁路全长为.
(2)解:设甲工程队后期每天施工.
甲工程队原来每天的施工长度为,
乙工程队每天的施工长度为.
根据题意,得,解得.
故甲工程队后期每天至少施工.
20.,整数解为:,,
【分析】本题考查的是求解不等式组的整数解,先分别解不等式组中的两个不等式,再确定解集的公共部分即可得到不等式组的解集,再确定整数解即可.
【详解】解:
由①得:
由②得:
所以不等式组的解为:
∴整数解为: 2,3,4.
21.
【分析】本题考查了不等式的基本性质,根据不等式两边加(或减)同一个数(或式子),不等号的方向不变,不等式两边乘(或除以)同一个负数,不等号的方向改变进行解答即可.
【详解】解:∵,
∴,
∴.
22.至少需要把龙眼加工成桂圆肉
【分析】此题考查了一元一次不等式的应用,明确题意列出一元一次不等式是解答本题的关键.
设把龙眼加工成桂圆肉,则有的龙眼加工成龙眼干,根据题意列出一元一次不等式求解即可.
【详解】解:设把龙眼加工成桂圆肉,则有的龙眼加工成龙眼干.
由题意,得,
解得.
答:至少需要把龙眼加工成桂圆肉.
23.(1)
(2)三种购买方案:型设备0台,型设备10台;型设备1台,型设备9台;型设备2台,型设备8台;
(3)购买型设备1台,型设备9台最省钱
【分析】(1)根据题意列出关于x、y的二元一次方程组,然后解方程即可;
(2)设购买型设备a台,则购买型设备台,根据题意列出关于a的不等式,然后解不等式,根据a为整数可求解;
(3)根据题意和(2)中所求得到或2,然后分别求得购买费用,比较大小即可.
【详解】(1)解:由题意,,
∴;
(2)解:设购买型设备a台,则购买型设备台,
根据题意,得且,
解得,又a为整数,
∴该治污公司有三种购买方案:型设备0台,型设备10台;型设备1台,型设备9台;型设备2台,型设备8台;
(3)解:由题意得,解得,
∴或2,
当时,买设备的费用为(元),
当时,买设备的费用为(元),
∵,
∴购买型设备1台,型设备9台最省钱.
【点睛】本题考查一元一次不等式的应用、二元一次方程组的应用,理解题意,找到题中等量和不等量关系并正确求解是解答的关键.
24.(1)该同学的身体描述为肥胖
(2)
【分析】本题考查了不等式的应用.
(1)先根据计算公式计算出,再根据表格得出结论即可;
(2)设在身高1.5米的前提下,设体重x千克后身体达到正常,根据题意列出不等式,解不等式即可.
【详解】(1)解:∵体重67.5千克,身高1.5米,
∴,
∴该同学的身体描述为肥胖;
(2)解:设在身高1.5米的前提下,设体重x千克后身体达到正常,
则,
∴解得,
∴该同学应该减轻体重的范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
