第五章轴对称与旋转同步练习(含解析)
图片预览
文档简介
中小学教育资源及组卷应用平台
第五章轴对称与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中是轴对称图形的是( )
A. B. C. D.
2.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④钟摆的运动;⑤荡秋千运动.属于旋转的有( )
A.2个 B.3个 C.4个 D.5个
3.在下列四个标志中,是由某个基本图形经过旋转得到的是( )
A. B. C. D.
4.中华文明,源远流长,中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )
A. B. C. D.
5.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在( )
A.区域①处 B.区域②处 C.区域③处 D.区域④处
6.某校学生为校运动会设计会标,在以下四个标志中,不是轴对称图形的是( )
A. B.
C. D.
7.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A. B. C. D.
8.下列图形中,与成轴对称的是( )
A. B.
C. D.
9.把一张正方形白纸沿对角线对折后,得到一个等腰直角三角形,接着将其沿底边上的高折叠后又得到一个更小的等腰直角三角形,在折叠后的这张纸上剪出一个花纹,展开后得到一个图案,该图案的对称轴的条数至少是( )
A.1 B.2 C.3 D.4
10.如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是( )
A. B. C. D.
11.将如图所示原图中的三角形绕点O旋转后,不能得到的图形是图( )
A. B.
C. D.
12.如图,关于直线进行轴对称变换后得到,下列结论中不正确的是( )
A. B.
C.垂直平分 D.
二、填空题
13.下图的虚线中,是该图形的对称轴的是 ,不是该图形的对称轴的是 .(填写序号)
14.如图,点D,E分别在的边上,将沿直线折叠后,点C与点A重合.若,的周长为17,则线段的长为 .
15.图中有阴影的三角形与 (填数字)三角形成轴对称?整个图形 (填是、否)轴对称图形吗?它共有 条对称轴?
16.如图,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形,可供选择的白色小正方形有 个.
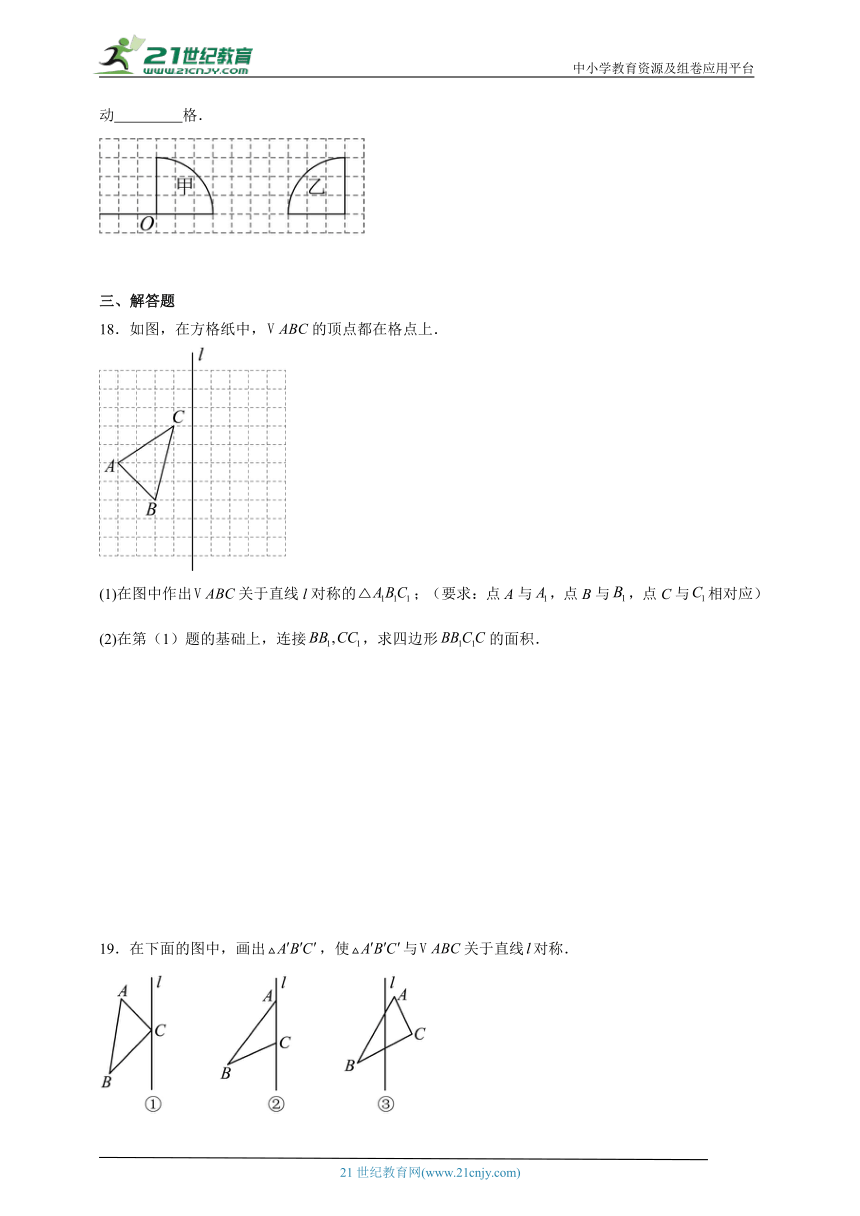
17.有如图,从图形甲到图形乙,所进行的图形运动是先绕点 时针旋转,再向右移动 格.
三、解答题
18.如图,在方格纸中,的顶点都在格点上.
(1)在图中作出关于直线l对称的;(要求:点A与,点B与,点C与相对应)
(2)在第(1)题的基础上,连接,求四边形的面积.
19.在下面的图中,画出,使与关于直线对称.
20.在如图的网格中,
(1)画,使它与关于对称;
(2)画,使它与关于对称;
(3)画出与的对称轴.
21.如图,是由经过轴对称变换得到的,直线是对称轴.
(1)与全等吗?
(2)分别找出点关于直线的对称点,如果点在内,那么点关于直线的对称点一定在内吗?
(3)连接,线段与直线有什么关系?
22.如图,把下列图形补成关于直线l对称的图形.
23.如图所示,直线是的对称轴,E,F是上的任意两点.若的面积为,求图中阴影部分的面积.
24.分别观察图(1)~(4)中的两个图形,判断它们是否分别关于某条直线成轴对称,并说明原因.
《第五章轴对称与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B D D C C B B A
题号 11 12
答案 D D
1.B
【分析】直接利用轴对称图形的定义进行判断.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【详解】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
【点睛】此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.B
【分析】本题考查了生活中的平移、旋转现象,熟练掌握平移与旋转的定义是解题的关键.
根据平移和旋转的定义对各小题分析判断即可.
【详解】解:①地下水位逐年下降,是平移现象;
②传送带的移动,是平移现象;
③方向盘的转动,是旋转现象;
④钟摆的运动,是旋转现象;
⑤荡秋千运动,是旋转现象.
属于旋转的有③④⑤共3个.
故选:B.
3.B
【分析】本题是考查运用旋转设计图案,根据旋转图形的特点解答即可.
【详解】解:A、不能旋转得到,错误;
B、可以旋转得到,正确;
C、不能旋转得到,错误;
D、不能旋转得到,错误;
故选:B.
4.D
【分析】本题主要考查了轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.根据轴对称图形的定义进行逐一判断即可.
【详解】解:A.不是轴对称图形,故A不符合题意;
B.不是轴对称图形,故B不符合题意;
C.不是轴对称图形,故C不符合题意;
D.是轴对称图形,故D符合题意.
故选:D.
5.D
【分析】直接利用轴对称图形的定义得出答案.
【详解】解:要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,
使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在区域④.
故选D.
【点睛】本题主要考查的是利用轴对称的性质设计图案,掌握轴对称图形的性质是解题的关键.
6.C
【分析】根据轴对称图形的概念逐项判断即可解答.
【详解】解:A、是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项符合题意;
D、是轴对称图形,故本选项不符合题意.
故选:C.
【点睛】本题主要考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
7.C
【分析】本题考查的是学生对旋转和平移的掌握程度,根据平移后的图形与原图形完全相同,旋转后的图形与原图形方向不同,形状大小相同逐项判断即可.
【详解】解:A.顺时针旋转即可得到该选项的图形,故不符合题意;
B.逆时针旋转即可得到该选项的图形,故不符合题意;
C.不能由图形M经过一次平移或旋转得到,故符合题意;
D.顺时针旋转即可得到该选项的图形,故不符合题意.
故选:C.
8.B
【分析】本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
根据成轴对称的性质对各选项分析判断即可得解.
【详解】解:A、不成轴对称,故本选项错误;
B、成轴对称,故本选项正确;
C、不成轴对称,故本选项错误;
D、不成轴对称,故本选项错误.
故选:B.
9.B
【分析】本题考查老师轴对称图形的性质,根据轴对称的性质或动手操作即可得出答案.
【详解】结合剪纸知识可知,对折一次至少有1条对称轴,对折两次至少有2条对称轴.
故选B.
10.A
【分析】根据轴对称的性质求解即可.
【详解】解:如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是A选项.
故选:A.
【点睛】本题考查利用轴对称设计图案,剪纸问题,解题的关键是理解轴对称图形的性质,属于中考常考题型.
11.D
【分析】根据旋转的意义解答即可.
本题考查了旋转的性质,熟练掌握性质是解题的关键.
【详解】解:逆时针旋转可得到A;
顺时针旋转可得到B;
顺时针旋转可得到C;
无法旋转得到D,
故选:D.
12.D
【分析】本题考查了轴对称的性质等知识,熟练掌握轴对称的性质是解题的关键.由轴对称的性质即可得出结论.
【详解】解:∵关于直线进行轴对称变换后得到,
∴,,垂直平分,,
故选项A、B、C正确;故选项D不一定正确.
故选:D.
13. ②④⑥ ①③⑤
【分析】本题考查了轴对称图形,解题的关键是掌握轴对称图形性质.
根据对称轴的性质找出对称轴即可求解.
【详解】是该图形的对称轴的是②④⑥,不是该图形的对称轴的是①③⑤.
故答案为:②④⑥,①③⑤.
14.
【分析】本题考查了翻折变换,三角形的周长,由翻折可得,进而得到,即可求解,根据题意得出是解题的关键.
【详解】解:∵点D,E分别在的边上,将沿直线折叠后,点C与点A重合,
∴,
∵,的周长为17,
∴,
∴,
故答案为:.
15. 、 是
【分析】本题考查了轴对称图形的定义,解题的关键是掌握轴对称图形的定义.根据一个图形沿某条直线折叠,直线两旁的部分能够重合,那么这个图形叫做轴对称图形,这条直线是它的对称轴,即可求解.
【详解】解:图中有阴影的三角形与、三角形成轴对称;
整个图形是轴对称图形,它共有条对称轴;
故答案为:、;是;.
16.5
【分析】本题考查了轴对称图形“如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形”,熟记定义是解题关键.根据轴对称图形的定义求解即可得.
【详解】解:如图,共有以下5种选取涂黑方法:
故答案为:5.
17. 逆 10
【分析】根据旋转性质及平移性质即可得到答案.
【详解】解:观察甲乙两图可知,将甲图以为旋转中心,逆时针旋转,再向右平移个单位长度即可得到乙图,
故答案为:逆;.
【点睛】本题考查旋转及平移性质,熟记旋转性质及平移性质作图是解决问题的关键.
18.(1)见解析
(2)12
【分析】此题主要考查了作轴对称变换,求四边形面积,
(1)根据轴对称的性质作图即可;
(2)由图得四边形是等腰梯形,,高是4,然后利用梯形的面积 求解即可.
【详解】(1)如图,是关于直线l的对称图形.
(2)由图得四边形是等腰梯形,,高是4.
19.见解析
【分析】据轴对称性,先找出点A、B、C关于直线l的对称点的位置,然后顺次连接即可.
【详解】解:如图所示,即为所求.
【点睛】本题考查了作图——轴对称变换:在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,一般的方法是:由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形.
20.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查轴作图对称变换、解题的关键是熟练掌握轴对称的性质,属于基础题,中考常考题型.
(1)分别画出、、关于对称点、、即可.
(2)分别画出、、即可关于的对称点、、即可.
(3)画出线段的垂直平分线即可.
【详解】(1)如图所示;
(2)如图所示;
(3)画出与的对称轴如图所示;
21.(1)与全等
(2)点关于直线的对称点分别是点;点关于直线的对称点一定在内
(3)线段被直线垂直平分
【分析】(1)根据对称轴图形的性质即可求解;
(2)根据对称轴图形的性质即可求解;
(3)根据对称轴图形的性质即可求解;
【详解】(1)解:与关于直线对称,
∴,
∴,
∴与全等.
(2)解:∵与关于直线对称,
∴点关于直线的对称点分别是点,点关于直线的对称点一定在内.
(3)解:∵与关于直线对称,且点的对称点是点,
∴点到直线的距离等于点到直线的距离,
∴线段被直线垂直平分.
【点睛】本题主要考查轴对称图形的定义,性质,掌握成轴对称的两个图形中任何一个图形都可以看成是由另一个图形经过轴对称变换得到;一个轴对称图形也可以看成是以它的一部分为基础经过轴对称变换而得到的;成轴对称图形的对应点的连线被对称轴垂直平分等知识是解题的关键.
22.见解析
【分析】根据轴对称图形的性质,先找出各关键点关于直线l的对称点,再顺次连接即可.
【详解】解:如图所示.
【点睛】本题考查作图-轴对称变换,解题的关键是掌握轴对称变换的性质,几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始.当点在对称轴上时,它关于对称轴的对称点就是它本身;当点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
23.
【分析】本题考查了轴对称的性质,熟记性质并判断出阴影部分的面积等于的面积的一半是解题的关键.根据轴对称的性质判断出阴影部分的面积等于的面积的一半,然后计算即可得解.
【详解】解:∵直线是的对称轴,
∴和关于直线成轴对称,
∴.
∵E,F是上的任意两点,
∴与关于直线成轴对称.
∴.
∴阴影部分的面积.
24.图(1)(4)分别关于某条直线成轴对称;图(2)(3)不成轴对称,说明见解析
【分析】本题考查轴对称图形的判定,轴对称图形定义:如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,根据定义逐项判定即可得出结论,熟练掌握轴对称图形的定义是解决问题的关键.
【详解】解:图(1)(4)分别关于某条直线成轴对称;图(2)(3)不成轴对称,
原因如下:
图(1)(4)分别关于某条直线成轴对称,因为沿某一直线对折,每一组的两个图形都可以完全重合(这里的“完全重合”是指必须沿某直线折叠后完全重合,这就要求两个图形必须形状相同、大小相等,同时还对两个图形的位置作了限定);
图(2)(3)不成轴对称,因为不能找到它们的对称轴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第五章轴对称与旋转
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列图形中是轴对称图形的是( )
A. B. C. D.
2.下列现象中:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④钟摆的运动;⑤荡秋千运动.属于旋转的有( )
A.2个 B.3个 C.4个 D.5个
3.在下列四个标志中,是由某个基本图形经过旋转得到的是( )
A. B. C. D.
4.中华文明,源远流长,中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )
A. B. C. D.
5.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在( )
A.区域①处 B.区域②处 C.区域③处 D.区域④处
6.某校学生为校运动会设计会标,在以下四个标志中,不是轴对称图形的是( )
A. B.
C. D.
7.下列图形中,不能由图形M经过一次平移或旋转得到的是( )
A. B. C. D.
8.下列图形中,与成轴对称的是( )
A. B.
C. D.
9.把一张正方形白纸沿对角线对折后,得到一个等腰直角三角形,接着将其沿底边上的高折叠后又得到一个更小的等腰直角三角形,在折叠后的这张纸上剪出一个花纹,展开后得到一个图案,该图案的对称轴的条数至少是( )
A.1 B.2 C.3 D.4
10.如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是( )
A. B. C. D.
11.将如图所示原图中的三角形绕点O旋转后,不能得到的图形是图( )
A. B.
C. D.
12.如图,关于直线进行轴对称变换后得到,下列结论中不正确的是( )
A. B.
C.垂直平分 D.
二、填空题
13.下图的虚线中,是该图形的对称轴的是 ,不是该图形的对称轴的是 .(填写序号)
14.如图,点D,E分别在的边上,将沿直线折叠后,点C与点A重合.若,的周长为17,则线段的长为 .
15.图中有阴影的三角形与 (填数字)三角形成轴对称?整个图形 (填是、否)轴对称图形吗?它共有 条对称轴?
16.如图,在的正方形网格中,黑色部分的图形构成一个轴对称图形,现在任意选取一个白色的小正方形并涂黑,使黑色部分的图形仍然构成一个轴对称图形,可供选择的白色小正方形有 个.
17.有如图,从图形甲到图形乙,所进行的图形运动是先绕点 时针旋转,再向右移动 格.
三、解答题
18.如图,在方格纸中,的顶点都在格点上.
(1)在图中作出关于直线l对称的;(要求:点A与,点B与,点C与相对应)
(2)在第(1)题的基础上,连接,求四边形的面积.
19.在下面的图中,画出,使与关于直线对称.
20.在如图的网格中,
(1)画,使它与关于对称;
(2)画,使它与关于对称;
(3)画出与的对称轴.
21.如图,是由经过轴对称变换得到的,直线是对称轴.
(1)与全等吗?
(2)分别找出点关于直线的对称点,如果点在内,那么点关于直线的对称点一定在内吗?
(3)连接,线段与直线有什么关系?
22.如图,把下列图形补成关于直线l对称的图形.
23.如图所示,直线是的对称轴,E,F是上的任意两点.若的面积为,求图中阴影部分的面积.
24.分别观察图(1)~(4)中的两个图形,判断它们是否分别关于某条直线成轴对称,并说明原因.
《第五章轴对称与旋转》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B D D C C B B A
题号 11 12
答案 D D
1.B
【分析】直接利用轴对称图形的定义进行判断.如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形.
【详解】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
【点睛】此题主要考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.B
【分析】本题考查了生活中的平移、旋转现象,熟练掌握平移与旋转的定义是解题的关键.
根据平移和旋转的定义对各小题分析判断即可.
【详解】解:①地下水位逐年下降,是平移现象;
②传送带的移动,是平移现象;
③方向盘的转动,是旋转现象;
④钟摆的运动,是旋转现象;
⑤荡秋千运动,是旋转现象.
属于旋转的有③④⑤共3个.
故选:B.
3.B
【分析】本题是考查运用旋转设计图案,根据旋转图形的特点解答即可.
【详解】解:A、不能旋转得到,错误;
B、可以旋转得到,正确;
C、不能旋转得到,错误;
D、不能旋转得到,错误;
故选:B.
4.D
【分析】本题主要考查了轴对称图形的定义,如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.根据轴对称图形的定义进行逐一判断即可.
【详解】解:A.不是轴对称图形,故A不符合题意;
B.不是轴对称图形,故B不符合题意;
C.不是轴对称图形,故C不符合题意;
D.是轴对称图形,故D符合题意.
故选:D.
5.D
【分析】直接利用轴对称图形的定义得出答案.
【详解】解:要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,
使它与阴影部分组成的新图形是轴对称图形,则这个正方形应该添加在区域④.
故选D.
【点睛】本题主要考查的是利用轴对称的性质设计图案,掌握轴对称图形的性质是解题的关键.
6.C
【分析】根据轴对称图形的概念逐项判断即可解答.
【详解】解:A、是轴对称图形,故本选项不符合题意;
B、是轴对称图形,故本选项不符合题意;
C、不是轴对称图形,故本选项符合题意;
D、是轴对称图形,故本选项不符合题意.
故选:C.
【点睛】本题主要考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
7.C
【分析】本题考查的是学生对旋转和平移的掌握程度,根据平移后的图形与原图形完全相同,旋转后的图形与原图形方向不同,形状大小相同逐项判断即可.
【详解】解:A.顺时针旋转即可得到该选项的图形,故不符合题意;
B.逆时针旋转即可得到该选项的图形,故不符合题意;
C.不能由图形M经过一次平移或旋转得到,故符合题意;
D.顺时针旋转即可得到该选项的图形,故不符合题意.
故选:C.
8.B
【分析】本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.
根据成轴对称的性质对各选项分析判断即可得解.
【详解】解:A、不成轴对称,故本选项错误;
B、成轴对称,故本选项正确;
C、不成轴对称,故本选项错误;
D、不成轴对称,故本选项错误.
故选:B.
9.B
【分析】本题考查老师轴对称图形的性质,根据轴对称的性质或动手操作即可得出答案.
【详解】结合剪纸知识可知,对折一次至少有1条对称轴,对折两次至少有2条对称轴.
故选B.
10.A
【分析】根据轴对称的性质求解即可.
【详解】解:如图是嘉嘉把纸折叠后剪出的图案,将剪纸展开后得到的图案是A选项.
故选:A.
【点睛】本题考查利用轴对称设计图案,剪纸问题,解题的关键是理解轴对称图形的性质,属于中考常考题型.
11.D
【分析】根据旋转的意义解答即可.
本题考查了旋转的性质,熟练掌握性质是解题的关键.
【详解】解:逆时针旋转可得到A;
顺时针旋转可得到B;
顺时针旋转可得到C;
无法旋转得到D,
故选:D.
12.D
【分析】本题考查了轴对称的性质等知识,熟练掌握轴对称的性质是解题的关键.由轴对称的性质即可得出结论.
【详解】解:∵关于直线进行轴对称变换后得到,
∴,,垂直平分,,
故选项A、B、C正确;故选项D不一定正确.
故选:D.
13. ②④⑥ ①③⑤
【分析】本题考查了轴对称图形,解题的关键是掌握轴对称图形性质.
根据对称轴的性质找出对称轴即可求解.
【详解】是该图形的对称轴的是②④⑥,不是该图形的对称轴的是①③⑤.
故答案为:②④⑥,①③⑤.
14.
【分析】本题考查了翻折变换,三角形的周长,由翻折可得,进而得到,即可求解,根据题意得出是解题的关键.
【详解】解:∵点D,E分别在的边上,将沿直线折叠后,点C与点A重合,
∴,
∵,的周长为17,
∴,
∴,
故答案为:.
15. 、 是
【分析】本题考查了轴对称图形的定义,解题的关键是掌握轴对称图形的定义.根据一个图形沿某条直线折叠,直线两旁的部分能够重合,那么这个图形叫做轴对称图形,这条直线是它的对称轴,即可求解.
【详解】解:图中有阴影的三角形与、三角形成轴对称;
整个图形是轴对称图形,它共有条对称轴;
故答案为:、;是;.
16.5
【分析】本题考查了轴对称图形“如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形”,熟记定义是解题关键.根据轴对称图形的定义求解即可得.
【详解】解:如图,共有以下5种选取涂黑方法:
故答案为:5.
17. 逆 10
【分析】根据旋转性质及平移性质即可得到答案.
【详解】解:观察甲乙两图可知,将甲图以为旋转中心,逆时针旋转,再向右平移个单位长度即可得到乙图,
故答案为:逆;.
【点睛】本题考查旋转及平移性质,熟记旋转性质及平移性质作图是解决问题的关键.
18.(1)见解析
(2)12
【分析】此题主要考查了作轴对称变换,求四边形面积,
(1)根据轴对称的性质作图即可;
(2)由图得四边形是等腰梯形,,高是4,然后利用梯形的面积 求解即可.
【详解】(1)如图,是关于直线l的对称图形.
(2)由图得四边形是等腰梯形,,高是4.
19.见解析
【分析】据轴对称性,先找出点A、B、C关于直线l的对称点的位置,然后顺次连接即可.
【详解】解:如图所示,即为所求.
【点睛】本题考查了作图——轴对称变换:在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始的,一般的方法是:由已知点出发向所给直线作垂线,并确定垂足;直线的另一侧,以垂足为一端点,作一条线段使之等于已知点和垂足之间的线段的长,得到线段的另一端点,即为对称点;连接这些对称点,就得到原图形的轴对称图形.
20.(1)见解析
(2)见解析
(3)见解析
【分析】本题考查轴作图对称变换、解题的关键是熟练掌握轴对称的性质,属于基础题,中考常考题型.
(1)分别画出、、关于对称点、、即可.
(2)分别画出、、即可关于的对称点、、即可.
(3)画出线段的垂直平分线即可.
【详解】(1)如图所示;
(2)如图所示;
(3)画出与的对称轴如图所示;
21.(1)与全等
(2)点关于直线的对称点分别是点;点关于直线的对称点一定在内
(3)线段被直线垂直平分
【分析】(1)根据对称轴图形的性质即可求解;
(2)根据对称轴图形的性质即可求解;
(3)根据对称轴图形的性质即可求解;
【详解】(1)解:与关于直线对称,
∴,
∴,
∴与全等.
(2)解:∵与关于直线对称,
∴点关于直线的对称点分别是点,点关于直线的对称点一定在内.
(3)解:∵与关于直线对称,且点的对称点是点,
∴点到直线的距离等于点到直线的距离,
∴线段被直线垂直平分.
【点睛】本题主要考查轴对称图形的定义,性质,掌握成轴对称的两个图形中任何一个图形都可以看成是由另一个图形经过轴对称变换得到;一个轴对称图形也可以看成是以它的一部分为基础经过轴对称变换而得到的;成轴对称图形的对应点的连线被对称轴垂直平分等知识是解题的关键.
22.见解析
【分析】根据轴对称图形的性质,先找出各关键点关于直线l的对称点,再顺次连接即可.
【详解】解:如图所示.
【点睛】本题考查作图-轴对称变换,解题的关键是掌握轴对称变换的性质,几何图形都可看做是由点组成,我们在画一个图形的轴对称图形时,也是先从确定一些特殊的对称点开始.当点在对称轴上时,它关于对称轴的对称点就是它本身;当点在对称轴一侧时,它关于对称轴的对称点在对称轴的另一侧.
23.
【分析】本题考查了轴对称的性质,熟记性质并判断出阴影部分的面积等于的面积的一半是解题的关键.根据轴对称的性质判断出阴影部分的面积等于的面积的一半,然后计算即可得解.
【详解】解:∵直线是的对称轴,
∴和关于直线成轴对称,
∴.
∵E,F是上的任意两点,
∴与关于直线成轴对称.
∴.
∴阴影部分的面积.
24.图(1)(4)分别关于某条直线成轴对称;图(2)(3)不成轴对称,说明见解析
【分析】本题考查轴对称图形的判定,轴对称图形定义:如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的图形叫做轴对称图形,根据定义逐项判定即可得出结论,熟练掌握轴对称图形的定义是解决问题的关键.
【详解】解:图(1)(4)分别关于某条直线成轴对称;图(2)(3)不成轴对称,
原因如下:
图(1)(4)分别关于某条直线成轴对称,因为沿某一直线对折,每一组的两个图形都可以完全重合(这里的“完全重合”是指必须沿某直线折叠后完全重合,这就要求两个图形必须形状相同、大小相等,同时还对两个图形的位置作了限定);
图(2)(3)不成轴对称,因为不能找到它们的对称轴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
