4.5垂线同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
4.5垂线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下图用几何符号可以表示为( )
A. B. C. D.
2.如图,已知A为直线l外一定点,B为直线l上一动点.则下列说法正确的是( ).
A.当点B自左向右移动时,A,B两点间的距离越来越小
B.连接AB,则线段AB的长度即为点A到直线l的距离
C.过点A有且只有一条直线与直线l平行
D.同一平面内,过点A有两条直线与直线l垂直
3.下列说法正确的有( )
①一条直线的垂线有且只有一条;②过直线上一点有且只有一条直线与已知直线垂直;③在同一平面内,过直线外一点有无数条直线与已知直线垂直;④在同一平面内,可以过任意一点画已知直线的垂线.
A.1个 B.2个 C.3个 D.4个
4.在一个无风的日子,一辆汽车在直线形的公路上由向行驶,如图,是学校的位置,当汽车行驶到下列哪一位置时,学校受汽车噪声的影响最大( )
A.点 B.点 C.点 D.点
5.在下列说法中,正确的有( )
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
A.个 B.个 C.个 D.个
6.如图,,,垂足为点O,,垂足为点O,则等于( )
A.24° B.42° C.48° D.64°
7.已知线段的长为10,点A,B到直线l的距离分别为6和4,则符合条件的直线有( )
A.1条 B.2条 C.3条 D.4条
8.如图,点A,E,B在同一条直线上,,若,则的度数是( )
A. B. C. D.
9.如图所示,直线,直线c与直线a,b分别交于点D,E,射线直线c,若,则的度数是( )
A. B. C. D.
10.下列说法正确的有( )
A.相等的角是对顶角
B.直线外一点到已知直线的垂线段叫做点到该直线的距离
C.两条不相交的直线叫做平行线
D.在同一平面内,若直线,,则直线
11.如果直线直线,直线直线,那么与重合(即,,三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
12.下列选项中,过点画直线的垂线,三角尺的摆放方式正确的是( )
A. B.
C. D.
二、填空题
13.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
14.如图,沿笔直小路的一侧栽植两棵小树,小明在处测得米,米,则点到的距离可能为 .
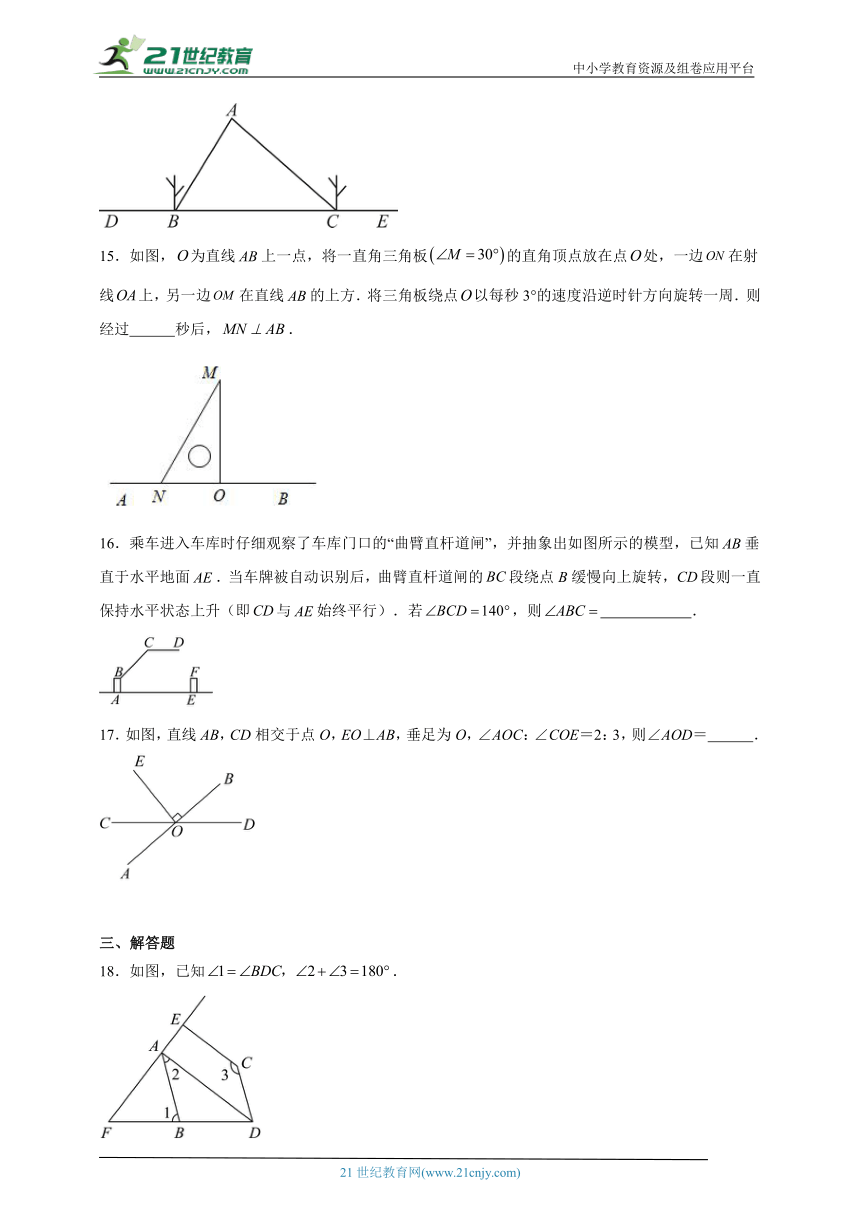
15.如图,为直线上一点,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的上方.将三角板绕点以每秒3°的速度沿逆时针方向旋转一周.则经过 秒后,.
16.乘车进入车库时仔细观察了车库门口的“曲臂直杆道闸”,并抽象出如图所示的模型,已知垂直于水平地面.当车牌被自动识别后,曲臂直杆道闸的段绕点B缓慢向上旋转,段则一直保持水平状态上升(即与始终平行).若,则 .
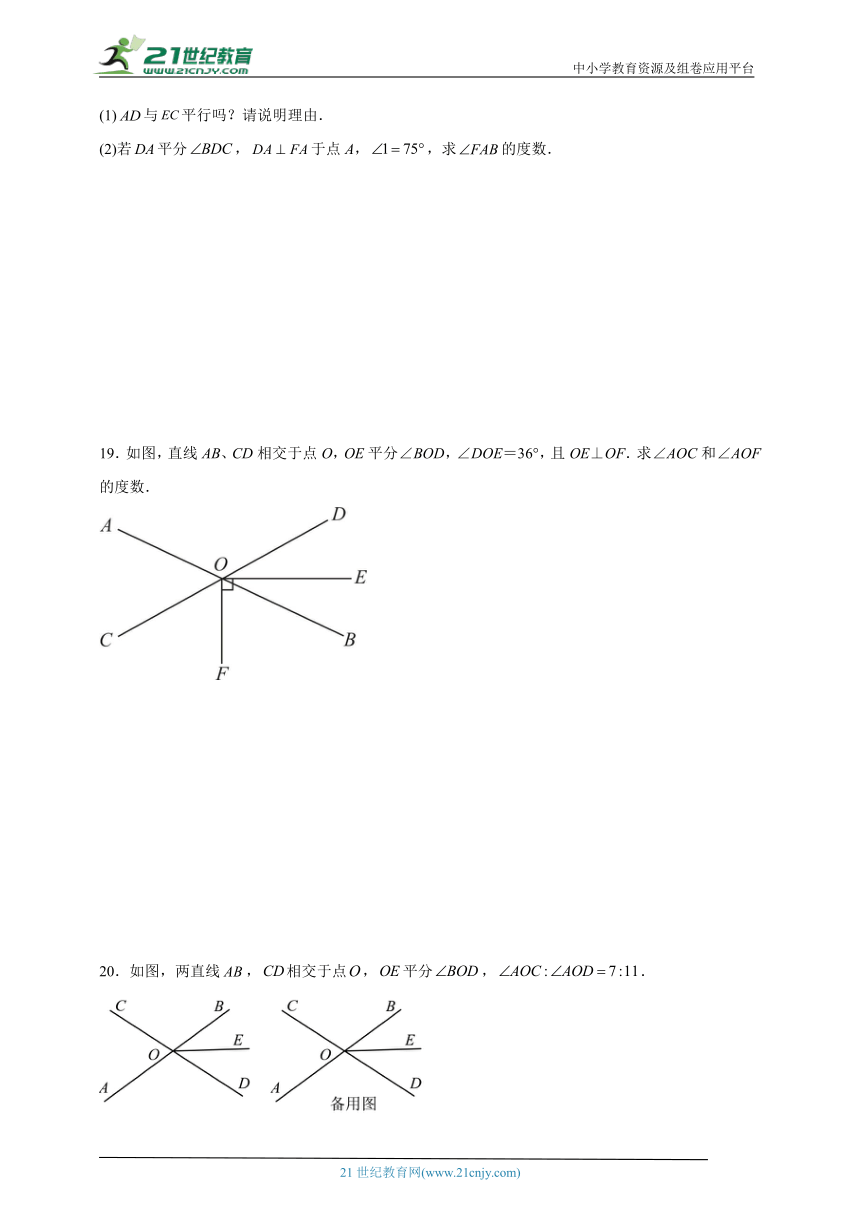
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=2:3,则∠AOD= .
三、解答题
18.如图,已知.
(1)与平行吗?请说明理由.
(2)若平分,于点A,,求的度数.
19.如图,直线AB、CD相交于点O,OE平分∠BOD,∠DOE=36°,且OE⊥OF.求∠AOC和∠AOF的度数.
20.如图,两直线,相交于点,平分,.
(1)求的度数;
(2)若射线,请在图中画出,并求的度数.
21.如图,已知A,B是直线l上两点,C是直线l外一点.
(1)画射线AC,线段BC;
(2)过点C作l的垂线段.
22.如图,点P,Q分别是的边外的点.
(1)过点P画的垂线,交于点C,交于点D.
(2)过点Q画的垂线交于点E,交于点F.
23.如图,在直角三角形中,,.
(1)点B到的距离是_____________;点A到的距离是_____________.
(2)画出表示点C到的距离的线段,并求出这个距离.
24.如图,分别过点作直线的垂线.
《4.5垂线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A B B B C A D D
题号 11 12
答案 C C
1.D
【分析】根据图形含义可得两直线互相垂直,再表示即可.
【详解】解:由图形含义可表示为:,
故选D
【点睛】本题考查的是两条直线互相垂直的表示,熟记垂直的表示方法是解本题的关键.
2.C
【分析】根据点到直线的距离,垂线及平行线的性质,依次判断即可.
【详解】解:A、当点B自左向右移动时,A,B两点间的距离先变小后变大,选项错误;
B、当AB⊥l时,线段AB的长度即为点A到直线l的距离,选项错误;
C、过点A有且只有一条直线与直线l平行,选项正确;
D、同一平面内,过点A有一条直线与直线l垂直,选项错误;
故选:C.
【点睛】题目主要考查点到直线的距离,垂线及平行线的性质,理解题意,综合运用这些知识点是解题关键.
3.A
【分析】本题考查了对垂线的定义的理解,牢记:“在同一平面内,过一点有且只有一条直线与已知直线垂直”是做题的关键;根据垂线的定义,逐项判断即可;
【详解】解:①一条直线的垂线有无数条,故①不符合题意;
②在同一平面内,过直线上一点有且只有一条直线与已知直线垂直,故②不符合题意;
③在同一平面内,过直线外一点有且只有一条直线与已知直线垂直,故③不符合题意;
④在同一平面内,可以过任意一点画已知直线的垂线,故④符合题意;
所以正确的说法只有1个;
故选:A.
4.B
【分析】本题主要考查的是线段长度的比较,理解线段的长度是解题的关键.
【详解】由图可知:最短,
所以当汽车行驶到处时影响最大,
故选:B.
5.B
【分析】根据直线的性质,平行线公理,垂线的性质,以及平行线的性质对各小题分析判断即可得解.
【详解】解:①两点确定一条直线,正确;
②应为过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
③应为在同一平面内,垂直于同一条直线的两条直线平行,故本小题错误;
④平行于同一条直线的两条直线平行,正确;
⑤应为在同一个平面内,过一点有且只有一条直线和已知直线垂直,故本小题错误;
综上所述,说法正确的有①④共2个.
故选B.
【点睛】本题考查了平行线的性质,直线的性质,平行公理以及垂线的性质,熟记性质与概念是解题的关键.
6.B
【分析】根据,,可得∠BOD=∠AOC=90°,再由,可得∠AOB=48°,即可求解.
【详解】解:∵,,
∴∠BOD=∠AOC=90°,
∵,
∴∠AOB=∠AOD-∠BOD=48°,
∴∠BOC=∠AOC-∠AOB=42°.
故选:B
【点睛】本题主要考查了角与角间的和与差,垂直的性质,明确题意,准确得到角与角之间的关系是解题的关键.
7.C
【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
【详解】解:在线段的两旁可分别画一条满足条件的直线;
作线段的垂线,将线段分成6,4两部分,
所以符合条件的直线有3条,
故选:C.
【点睛】本题考查了点到直线的距离,即直线外一点到这条直线的垂线段的长度,注意距离都是非负数.
8.A
【分析】本题考查了垂线,根据平角的定义并结合图形进行分析是解题的关键.
先根据垂直定义可得,然后利用平角定义进行计算,即可解答.
【详解】解:,
,
,
,
故选:A.
9.D
【分析】本题主要考查了平行线的性质,由平行线的性质可得:,由垂直的定义可求出的度数,即可求得.熟记平行线的性质是解决问题的关键.
【详解】解:∵,
∴,
∵直线c,
∴,
∵,
∴,
∴.
故选:D.
10.D
【分析】根据对顶角的定义,点到直线的距离的定义,平行线的判定等知识,一一判断即可.
【详解】解:A、相等的角是对顶角,错误,相等的角不一定是对顶角,本选项不符合题意;
B、直线外一点到已知直线的垂线段叫做点到该直线的距离,错误,应该是直线外一点到已知直线的垂线段的长度叫做点到该直线的距离,本选项不符合题意;
C、两条不相交的直线叫做平行线,错误,条件是在同一平面内,本选项不符合题意;
D、在同一平面内,若直线,,则直线正确,本选项符合题意.
故选:D.
【点睛】本题考查对顶角的定义,点到直线的距离的定义,平行线的判定等知识,解题的关键是掌握基本知识,属于中考常考题型.
11.C
【分析】利用垂线的性质解答.
【详解】解:如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),
其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
【点睛】本题主要考查了垂线,关键是掌握垂线的性质.
12.C
【分析】根据画垂线的方法进行判断即可.
【详解】解:∵三角板有一个角是直角,
∴三角板的一条直角边与直线重合,
∵过点P作直线的垂线,
∴三角板的另一条直角边过点P,
∴符合上述条件的图形只有选项C.
故选:C.
【点睛】本题主要考查了用三角板画垂线,解题的关键是熟练掌握用三角板画垂线的方法.
13. 垂线 垂足
【解析】略
14.6米(答案不唯一)
【分析】本题考查了点到直线的距离,掌握点到直线,垂线段最短是解题的关键.
根据,点到直线,垂线段最短即可求解.
【详解】解:根据题意,,
∴点到的距离,即点到的垂线段长度要小于米,
∴点到的距离可能为米(答案不唯一),
故答案为:米(答案不唯一) .
15.10或70/70或10
【分析】分两种情况讨论,利用旋转的性质即可求解.
【详解】解:如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴(秒);
如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴旋转角为,
∴(秒);
故答案为:10或70.
【点睛】本题考查了垂直的定义、角的和差等知识,解题的关键是理解题意,画出图形,利用垂直的定义求解即可.
16./130度
【分析】此题主要考查了平行线的判定和性质,过点B向右侧作,利用平行线的性质得,即可得,再由得,进而得,从而可得出答案.
【详解】解:过点B向右侧作,则.
∵,
∴,
∵,,
∴,
又∵,
∴,
∴,
∴.
故答案为:.
17.144°
【分析】直接利用垂直的定义得出∠AOE=90°,进而利用∠AOC:∠COE=2:3,得出∠AOC的度数,进而得出答案.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
∵∠AOC:∠COE=2:3,
∴设∠AOC=2x,∠COE=3x,
则3x+2x=90°,
解得:x=18°,
故∠AOC=36°,
则∠AOD=180°-36°=144°.
故答案为:144°.
【点睛】此题主要考查了垂直的定义以及邻补角,正确得出∠AOC度数是解题关键.
18.(1),理由见解析
(2)
【分析】本题考查了平行线的判定与性质,角平分线的定义,两直线垂直的定义,熟练掌握平行线的判定与性质是解题的关键.
(1)由可得,进一步可推得,即可证明;
(2)由角平分线的定义可得,结合(1)的结论可推得,根据两直线垂直的定义可得,由此即得答案.
【详解】(1)解:,理由如下:
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵平分,,
∴,
∵,
∴,
∵,
∴,
∴。
19.
【分析】根据角平分线的意义以及对顶角相等求得,根据OE⊥OF以及平角的定义求得,根据即可求得的度数.
【详解】解: OE平分∠BOD,∠DOE=36°,
OE⊥OF
【点睛】本题考查了与角平分线有关的计算,垂直的定义,平角的定义,几何图形中角度的计算,数形结合是解题的关键.
20.(1)
(2)见解析,或
【分析】(1)根据已知得出,,根据对顶角相等得出,根据角平分线的定义得出,根据邻补角相等即可求解;
(2)分在内和内两种情况分别画出图形,即可求解.
【详解】(1)解:∵,,
∴,,
∴.
又∵平分,
∴,
∴.
(2)分两种情况:
如图①,∵,∴,
∴.
如图②,.
综上,的度数为或.
【点睛】本题考查了垂直的定义,角平分线的定义,对顶角相等,几何图形中角度的计算,数形结合是解题的关键.
21.(1)见详解
(2)见详解
【分析】本题考查了作图复杂作图,射线,线段,垂线段,解决本题的关键是掌握基本作图方法.
(1)根据射线、线段的定义即可画出射线,线段即可;
(2)根据垂线的定义,画出过点作的垂线段即可.
【详解】(1)解:如图,射线,线段即为所作;
(2)如图,垂线段即为所作.
22.(1)见解析
(2)见解析
【分析】本题考查作图 -基本作图,垂线等知识,解题的关键是理解垂线的定义,属于基础题.
(1)根据垂线的定义画出图形即可;
(2)根据垂线的定义画出图形即可.
【详解】(1)解:如图直线即为所作:
(2)解:如上图,直线即为所作.
23.(1)8; 6
(2)图见解析;点C到的距离是
【分析】本题考查了点到直线的距离,熟练掌握点到直线的距离的概念及等面积法是解题的关键,
(1)根据点到直线的距离的概念进行求解即可得到答案;
(2)过点作,则线段表示点C到的距离,再利用等面积法即可求得线段的长.
【详解】(1)解:∵三角形为直角三角形,,,
∵,
∴点B到的距离是的长度为8,
∵
∴点A到的距离是的长度为6.
故答案为:8;6.
(2)解:过点作,如图,线段即为所求.
,即,
,
∴点C到的距离是.
24.见解析
【分析】本题考查了学生利用直尺和三角板作垂线的能力,掌握以上知识是解答本题的关键.
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可;
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可;
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可.
【详解】解:如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.5垂线
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下图用几何符号可以表示为( )
A. B. C. D.
2.如图,已知A为直线l外一定点,B为直线l上一动点.则下列说法正确的是( ).
A.当点B自左向右移动时,A,B两点间的距离越来越小
B.连接AB,则线段AB的长度即为点A到直线l的距离
C.过点A有且只有一条直线与直线l平行
D.同一平面内,过点A有两条直线与直线l垂直
3.下列说法正确的有( )
①一条直线的垂线有且只有一条;②过直线上一点有且只有一条直线与已知直线垂直;③在同一平面内,过直线外一点有无数条直线与已知直线垂直;④在同一平面内,可以过任意一点画已知直线的垂线.
A.1个 B.2个 C.3个 D.4个
4.在一个无风的日子,一辆汽车在直线形的公路上由向行驶,如图,是学校的位置,当汽车行驶到下列哪一位置时,学校受汽车噪声的影响最大( )
A.点 B.点 C.点 D.点
5.在下列说法中,正确的有( )
①两点确定一条直线;
②过一点有且只有一条直线与已知直线平行;
③垂直于同一条直线的两条直线垂直;
④平行于同一条直线的两条直线平行;
⑤过一点有且只有一条直线和已知直线垂直.
A.个 B.个 C.个 D.个
6.如图,,,垂足为点O,,垂足为点O,则等于( )
A.24° B.42° C.48° D.64°
7.已知线段的长为10,点A,B到直线l的距离分别为6和4,则符合条件的直线有( )
A.1条 B.2条 C.3条 D.4条
8.如图,点A,E,B在同一条直线上,,若,则的度数是( )
A. B. C. D.
9.如图所示,直线,直线c与直线a,b分别交于点D,E,射线直线c,若,则的度数是( )
A. B. C. D.
10.下列说法正确的有( )
A.相等的角是对顶角
B.直线外一点到已知直线的垂线段叫做点到该直线的距离
C.两条不相交的直线叫做平行线
D.在同一平面内,若直线,,则直线
11.如果直线直线,直线直线,那么与重合(即,,三点共线),其理由是( )
A.两点确定一条直线
B.在同一平面内,过两点有且只有一条直线与已知直线垂直
C.在同一平面内,过一点有且只有一条直线与已知直线垂直
D.两点之间,线段最短
12.下列选项中,过点画直线的垂线,三角尺的摆放方式正确的是( )
A. B.
C. D.
二、填空题
13.垂直是相交的一种特殊情形,两条直线互相垂直,其中的一条直线叫做另一条直线的 ,它们的交点叫做 .
14.如图,沿笔直小路的一侧栽植两棵小树,小明在处测得米,米,则点到的距离可能为 .
15.如图,为直线上一点,将一直角三角板的直角顶点放在点处,一边在射线上,另一边在直线的上方.将三角板绕点以每秒3°的速度沿逆时针方向旋转一周.则经过 秒后,.
16.乘车进入车库时仔细观察了车库门口的“曲臂直杆道闸”,并抽象出如图所示的模型,已知垂直于水平地面.当车牌被自动识别后,曲臂直杆道闸的段绕点B缓慢向上旋转,段则一直保持水平状态上升(即与始终平行).若,则 .
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=2:3,则∠AOD= .
三、解答题
18.如图,已知.
(1)与平行吗?请说明理由.
(2)若平分,于点A,,求的度数.
19.如图,直线AB、CD相交于点O,OE平分∠BOD,∠DOE=36°,且OE⊥OF.求∠AOC和∠AOF的度数.
20.如图,两直线,相交于点,平分,.
(1)求的度数;
(2)若射线,请在图中画出,并求的度数.
21.如图,已知A,B是直线l上两点,C是直线l外一点.
(1)画射线AC,线段BC;
(2)过点C作l的垂线段.
22.如图,点P,Q分别是的边外的点.
(1)过点P画的垂线,交于点C,交于点D.
(2)过点Q画的垂线交于点E,交于点F.
23.如图,在直角三角形中,,.
(1)点B到的距离是_____________;点A到的距离是_____________.
(2)画出表示点C到的距离的线段,并求出这个距离.
24.如图,分别过点作直线的垂线.
《4.5垂线》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A B B B C A D D
题号 11 12
答案 C C
1.D
【分析】根据图形含义可得两直线互相垂直,再表示即可.
【详解】解:由图形含义可表示为:,
故选D
【点睛】本题考查的是两条直线互相垂直的表示,熟记垂直的表示方法是解本题的关键.
2.C
【分析】根据点到直线的距离,垂线及平行线的性质,依次判断即可.
【详解】解:A、当点B自左向右移动时,A,B两点间的距离先变小后变大,选项错误;
B、当AB⊥l时,线段AB的长度即为点A到直线l的距离,选项错误;
C、过点A有且只有一条直线与直线l平行,选项正确;
D、同一平面内,过点A有一条直线与直线l垂直,选项错误;
故选:C.
【点睛】题目主要考查点到直线的距离,垂线及平行线的性质,理解题意,综合运用这些知识点是解题关键.
3.A
【分析】本题考查了对垂线的定义的理解,牢记:“在同一平面内,过一点有且只有一条直线与已知直线垂直”是做题的关键;根据垂线的定义,逐项判断即可;
【详解】解:①一条直线的垂线有无数条,故①不符合题意;
②在同一平面内,过直线上一点有且只有一条直线与已知直线垂直,故②不符合题意;
③在同一平面内,过直线外一点有且只有一条直线与已知直线垂直,故③不符合题意;
④在同一平面内,可以过任意一点画已知直线的垂线,故④符合题意;
所以正确的说法只有1个;
故选:A.
4.B
【分析】本题主要考查的是线段长度的比较,理解线段的长度是解题的关键.
【详解】由图可知:最短,
所以当汽车行驶到处时影响最大,
故选:B.
5.B
【分析】根据直线的性质,平行线公理,垂线的性质,以及平行线的性质对各小题分析判断即可得解.
【详解】解:①两点确定一条直线,正确;
②应为过直线外一点有且只有一条直线与已知直线平行,故本小题错误;
③应为在同一平面内,垂直于同一条直线的两条直线平行,故本小题错误;
④平行于同一条直线的两条直线平行,正确;
⑤应为在同一个平面内,过一点有且只有一条直线和已知直线垂直,故本小题错误;
综上所述,说法正确的有①④共2个.
故选B.
【点睛】本题考查了平行线的性质,直线的性质,平行公理以及垂线的性质,熟记性质与概念是解题的关键.
6.B
【分析】根据,,可得∠BOD=∠AOC=90°,再由,可得∠AOB=48°,即可求解.
【详解】解:∵,,
∴∠BOD=∠AOC=90°,
∵,
∴∠AOB=∠AOD-∠BOD=48°,
∴∠BOC=∠AOC-∠AOB=42°.
故选:B
【点睛】本题主要考查了角与角间的和与差,垂直的性质,明确题意,准确得到角与角之间的关系是解题的关键.
7.C
【分析】根据从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
【详解】解:在线段的两旁可分别画一条满足条件的直线;
作线段的垂线,将线段分成6,4两部分,
所以符合条件的直线有3条,
故选:C.
【点睛】本题考查了点到直线的距离,即直线外一点到这条直线的垂线段的长度,注意距离都是非负数.
8.A
【分析】本题考查了垂线,根据平角的定义并结合图形进行分析是解题的关键.
先根据垂直定义可得,然后利用平角定义进行计算,即可解答.
【详解】解:,
,
,
,
故选:A.
9.D
【分析】本题主要考查了平行线的性质,由平行线的性质可得:,由垂直的定义可求出的度数,即可求得.熟记平行线的性质是解决问题的关键.
【详解】解:∵,
∴,
∵直线c,
∴,
∵,
∴,
∴.
故选:D.
10.D
【分析】根据对顶角的定义,点到直线的距离的定义,平行线的判定等知识,一一判断即可.
【详解】解:A、相等的角是对顶角,错误,相等的角不一定是对顶角,本选项不符合题意;
B、直线外一点到已知直线的垂线段叫做点到该直线的距离,错误,应该是直线外一点到已知直线的垂线段的长度叫做点到该直线的距离,本选项不符合题意;
C、两条不相交的直线叫做平行线,错误,条件是在同一平面内,本选项不符合题意;
D、在同一平面内,若直线,,则直线正确,本选项符合题意.
故选:D.
【点睛】本题考查对顶角的定义,点到直线的距离的定义,平行线的判定等知识,解题的关键是掌握基本知识,属于中考常考题型.
11.C
【分析】利用垂线的性质解答.
【详解】解:如果直线ON⊥直线a,直线OM⊥直线a,那么OM与ON重合(即O,M,N三点共线),
其理由是在同一平面内,过一点有且只有一条直线与已知直线垂直,
故选:C.
【点睛】本题主要考查了垂线,关键是掌握垂线的性质.
12.C
【分析】根据画垂线的方法进行判断即可.
【详解】解:∵三角板有一个角是直角,
∴三角板的一条直角边与直线重合,
∵过点P作直线的垂线,
∴三角板的另一条直角边过点P,
∴符合上述条件的图形只有选项C.
故选:C.
【点睛】本题主要考查了用三角板画垂线,解题的关键是熟练掌握用三角板画垂线的方法.
13. 垂线 垂足
【解析】略
14.6米(答案不唯一)
【分析】本题考查了点到直线的距离,掌握点到直线,垂线段最短是解题的关键.
根据,点到直线,垂线段最短即可求解.
【详解】解:根据题意,,
∴点到的距离,即点到的垂线段长度要小于米,
∴点到的距离可能为米(答案不唯一),
故答案为:米(答案不唯一) .
15.10或70/70或10
【分析】分两种情况讨论,利用旋转的性质即可求解.
【详解】解:如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴(秒);
如图,,
∵,,
∴,,
∵将三角板绕点以每秒3°的速度沿逆时针方向旋转,
∴旋转角为,
∴(秒);
故答案为:10或70.
【点睛】本题考查了垂直的定义、角的和差等知识,解题的关键是理解题意,画出图形,利用垂直的定义求解即可.
16./130度
【分析】此题主要考查了平行线的判定和性质,过点B向右侧作,利用平行线的性质得,即可得,再由得,进而得,从而可得出答案.
【详解】解:过点B向右侧作,则.
∵,
∴,
∵,,
∴,
又∵,
∴,
∴,
∴.
故答案为:.
17.144°
【分析】直接利用垂直的定义得出∠AOE=90°,进而利用∠AOC:∠COE=2:3,得出∠AOC的度数,进而得出答案.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
∵∠AOC:∠COE=2:3,
∴设∠AOC=2x,∠COE=3x,
则3x+2x=90°,
解得:x=18°,
故∠AOC=36°,
则∠AOD=180°-36°=144°.
故答案为:144°.
【点睛】此题主要考查了垂直的定义以及邻补角,正确得出∠AOC度数是解题关键.
18.(1),理由见解析
(2)
【分析】本题考查了平行线的判定与性质,角平分线的定义,两直线垂直的定义,熟练掌握平行线的判定与性质是解题的关键.
(1)由可得,进一步可推得,即可证明;
(2)由角平分线的定义可得,结合(1)的结论可推得,根据两直线垂直的定义可得,由此即得答案.
【详解】(1)解:,理由如下:
∵,
∴,
∴,
∵,
∴,
∴;
(2)解:∵平分,,
∴,
∵,
∴,
∵,
∴,
∴。
19.
【分析】根据角平分线的意义以及对顶角相等求得,根据OE⊥OF以及平角的定义求得,根据即可求得的度数.
【详解】解: OE平分∠BOD,∠DOE=36°,
OE⊥OF
【点睛】本题考查了与角平分线有关的计算,垂直的定义,平角的定义,几何图形中角度的计算,数形结合是解题的关键.
20.(1)
(2)见解析,或
【分析】(1)根据已知得出,,根据对顶角相等得出,根据角平分线的定义得出,根据邻补角相等即可求解;
(2)分在内和内两种情况分别画出图形,即可求解.
【详解】(1)解:∵,,
∴,,
∴.
又∵平分,
∴,
∴.
(2)分两种情况:
如图①,∵,∴,
∴.
如图②,.
综上,的度数为或.
【点睛】本题考查了垂直的定义,角平分线的定义,对顶角相等,几何图形中角度的计算,数形结合是解题的关键.
21.(1)见详解
(2)见详解
【分析】本题考查了作图复杂作图,射线,线段,垂线段,解决本题的关键是掌握基本作图方法.
(1)根据射线、线段的定义即可画出射线,线段即可;
(2)根据垂线的定义,画出过点作的垂线段即可.
【详解】(1)解:如图,射线,线段即为所作;
(2)如图,垂线段即为所作.
22.(1)见解析
(2)见解析
【分析】本题考查作图 -基本作图,垂线等知识,解题的关键是理解垂线的定义,属于基础题.
(1)根据垂线的定义画出图形即可;
(2)根据垂线的定义画出图形即可.
【详解】(1)解:如图直线即为所作:
(2)解:如上图,直线即为所作.
23.(1)8; 6
(2)图见解析;点C到的距离是
【分析】本题考查了点到直线的距离,熟练掌握点到直线的距离的概念及等面积法是解题的关键,
(1)根据点到直线的距离的概念进行求解即可得到答案;
(2)过点作,则线段表示点C到的距离,再利用等面积法即可求得线段的长.
【详解】(1)解:∵三角形为直角三角形,,,
∵,
∴点B到的距离是的长度为8,
∵
∴点A到的距离是的长度为6.
故答案为:8;6.
(2)解:过点作,如图,线段即为所求.
,即,
,
∴点C到的距离是.
24.见解析
【分析】本题考查了学生利用直尺和三角板作垂线的能力,掌握以上知识是解答本题的关键.
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可;
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可;
用三角板的一条直角边与重合,沿重合的直线平移三角板,使三角板的另一条直角边和点重合,过点沿直角边向画直线即可.
【详解】解:如图所示:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
