第二章四边形同步练习（含解析）

中小学教育资源及组卷应用平台
第二章四边形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，在菱形中，M，N分别在，上，且， 与交于点O，连接，若，则的度数为（ ）
A．28° B．52° C．62° D．72°
2．下列四个银行标志中，是中心对称图形的标志是（ ）
A． B． C． D．
3．如图所示，在矩形ABCD中，∠DBC=29°，将矩形沿直线BD折叠，顶点C落在点E处，则∠ABE的度数是（ ）
A．29° B．32° C．22° D．61°
4．如图，菱形ABCD的周长为28，对角线AC，BD交于点O，E为AD的中点，则OE的长等于（　　）
A．2 B．3.5 C．7 D．14
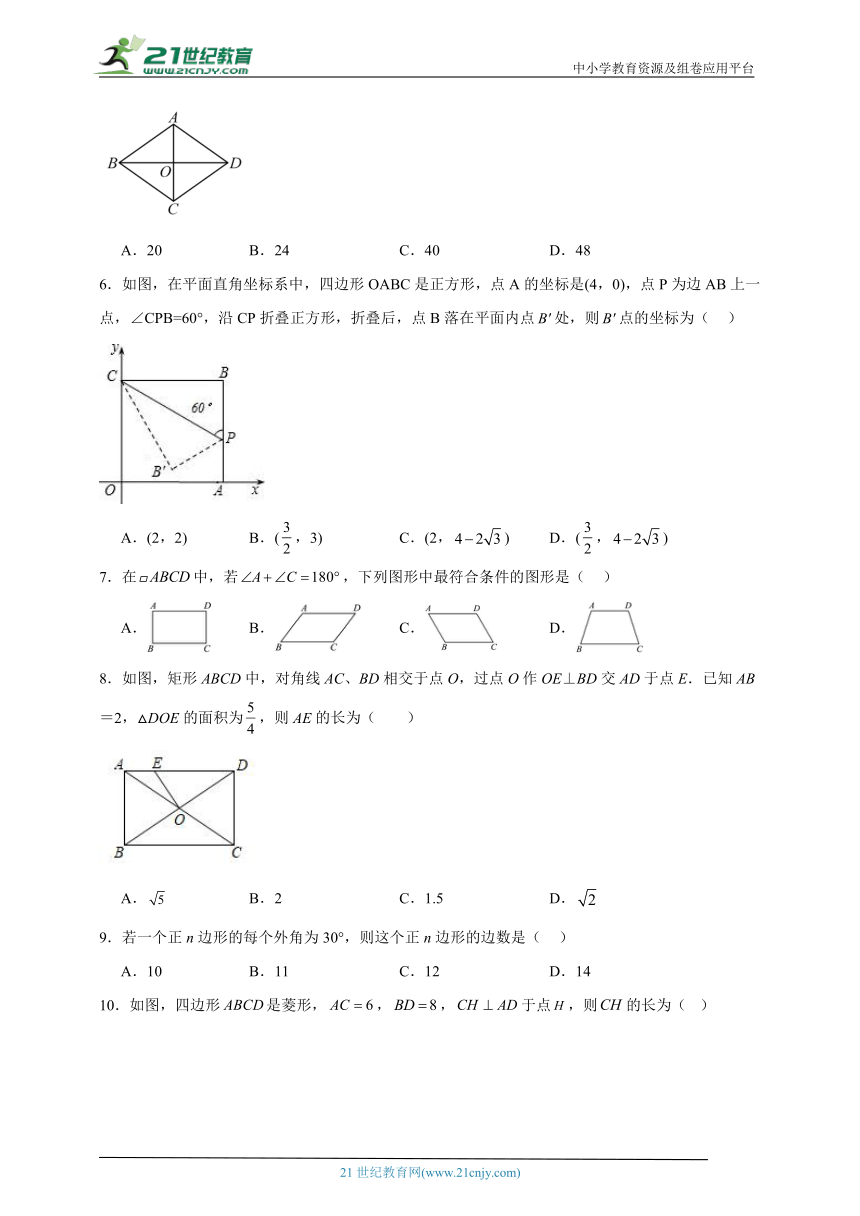
5．如图，菱形ABCD的对角线AC、BD的长分别为6和8，则这个菱形的周长是（　　）
A．20 B．24 C．40 D．48
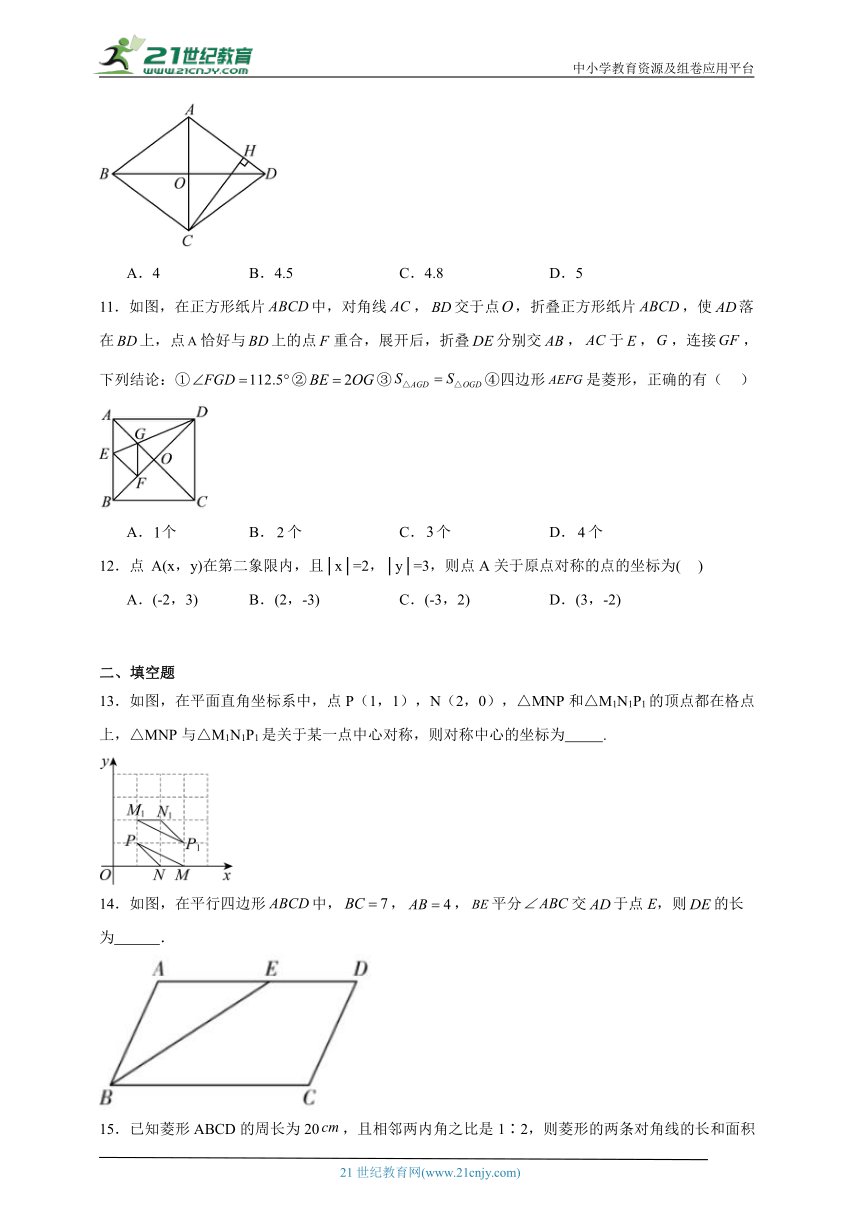
6．如图，在平面直角坐标系中，四边形OABC是正方形，点A的坐标是(4，0)，点P为边AB上一点，∠CPB=60°，沿CP折叠正方形，折叠后，点B落在平面内点处，则点的坐标为（ ）
A．(2，2) B．(，3) C．(2，) D．(，)
7．在中，若，下列图形中最符合条件的图形是（ ）
A． B． C． D．
8．如图，矩形ABCD中，对角线AC、BD相交于点O，过点O作OE⊥BD交AD于点E．已知AB＝2，△DOE的面积为，则AE的长为（　　）
A． B．2 C．1.5 D．
9．若一个正n边形的每个外角为30°，则这个正n边形的边数是（ ）
A．10 B．11 C．12 D．14
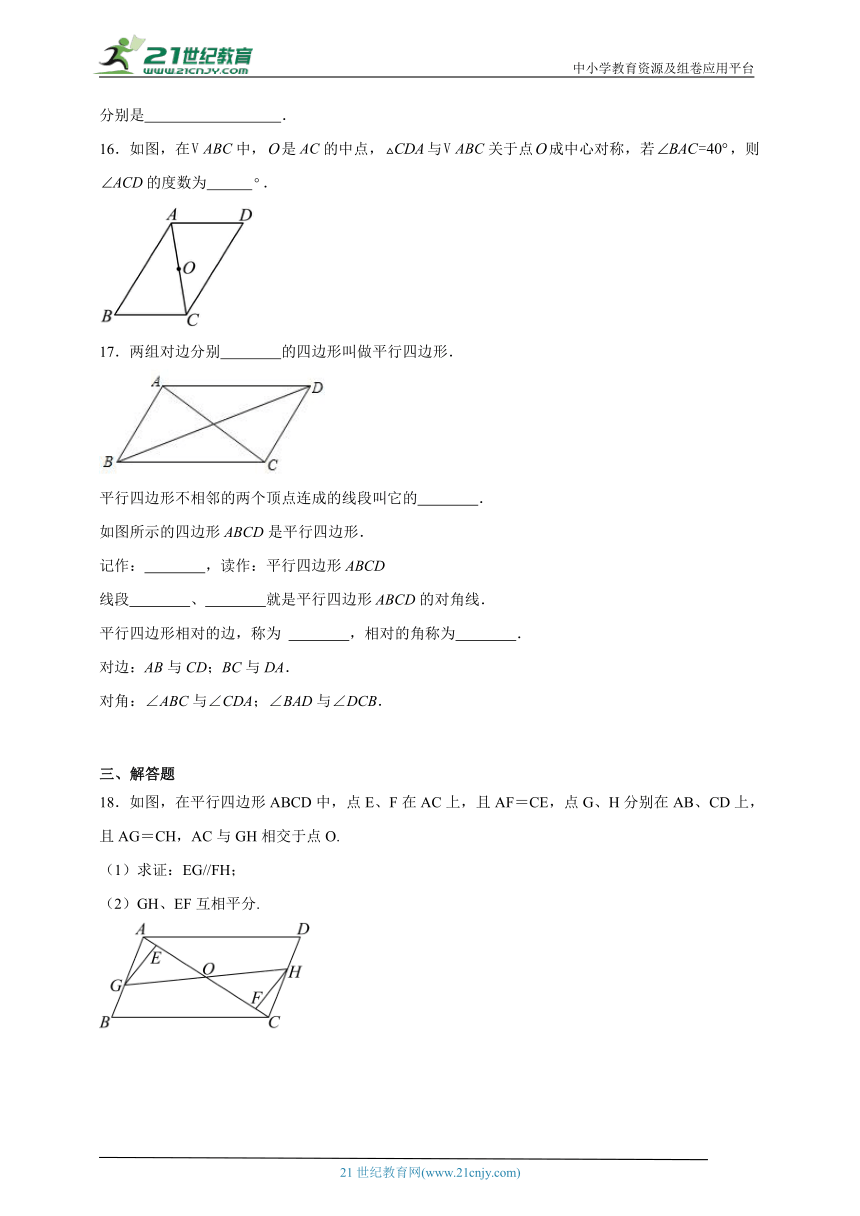
10．如图，四边形是菱形，，，于点，则的长为（ ）
A．4 B．4.5 C．4.8 D．5
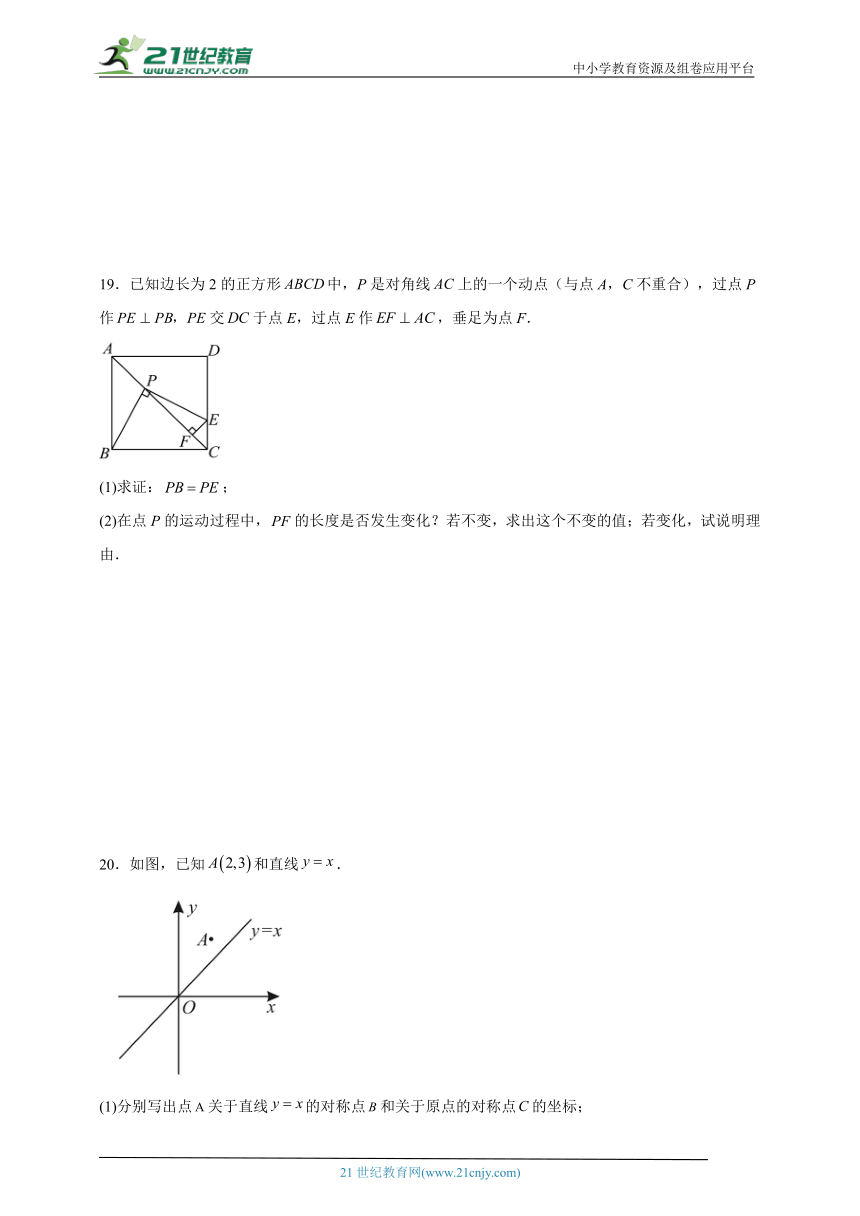
11．如图，在正方形纸片中，对角线，交于点，折叠正方形纸片，使落在上，点恰好与上的点重合，展开后，折叠分别交，于，，连接，下列结论：①②③④四边形是菱形，正确的有（ ）
A．个 B．个 C．个 D．个
12．点 A(x，y)在第二象限内，且│x│=2，│y│=3，则点A关于原点对称的点的坐标为( )
A．(-2，3) B．(2，-3) C．(-3，2) D．(3，-2)
二、填空题
13．如图，在平面直角坐标系中，点P（1，1），N（2，0），△MNP和△M1N1P1的顶点都在格点上，△MNP与△M1N1P1是关于某一点中心对称，则对称中心的坐标为 .
14．如图，在平行四边形中，，，平分交于点E，则的长为 ．
15．已知菱形ABCD的周长为20，且相邻两内角之比是1∶2，则菱形的两条对角线的长和面积分别是 ．
16．如图，在中，是的中点，与关于点成中心对称，若，则的度数为 ．
17．两组对边分别 的四边形叫做平行四边形．
平行四边形不相邻的两个顶点连成的线段叫它的 ．
如图所示的四边形ABCD是平行四边形．
记作： ，读作：平行四边形ABCD
线段 、 就是平行四边形ABCD的对角线．
平行四边形相对的边，称为 ，相对的角称为 ．
对边：AB与CD；BC与DA．
对角：∠ABC与∠CDA；∠BAD与∠DCB．
三、解答题
18．如图，在平行四边形ABCD中，点E、F在AC上，且AF＝CE，点G、H分别在AB、CD上，且AG＝CH，AC与GH相交于点O.
（1）求证：EG//FH；
（2）GH、EF互相平分.

19．已知边长为2的正方形中，P是对角线上的一个动点（与点A，C不重合），过点P作交于点E，过点E作，垂足为点F．
(1)求证：；
(2)在点P的运动过程中，的长度是否发生变化？若不变，求出这个不变的值；若变化，试说明理由．
20．如图，已知和直线．
(1)分别写出点关于直线的对称点和关于原点的对称点的坐标；
(2)若点是点关于原点的对称点，判断四边形的形状，并说明理由．
21．如图所示，已知四边形，，点F在的延长线上，连接交于E，E刚好为的中点．
(1)求证：；
(2)若点B为线段的中点，且，求的长．
22．在菱形ABCD中，点E为AB上一点，点F为BC延长线上一点，连接EF交AC于G．
(1)如图1，若点E为AB中点，，，求菱形ABCD的面积；
(2)如图2，过点F作于点H，．求证：；
(3)如图3，在（2）问的条件下，将线段CG绕点G旋转得线段，点M为中点，当，时，求HM的最大值．
23．已知：如图，点O是平行四边形的对角线的中点，E，F分别是和上的点，且．
(1)求证：四边形是平行四边形；
(2)求证：；
24．如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上的一个动点（不与点A重合），延长ME交CD的延长线于点N，连接MD，AN．
（1）求证：四边形AMDN是平行四边形．
（2）当AM的值为何值时，四边形AMDN是矩形，请说明理由．
《第二章四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B A C A C C C
题号 11 12
答案 C B
1．C
【分析】本题考查了菱形的性质和全等三角形的判定和性质，注意掌握菱形对边平行以及对角线相互垂直的性质．
根据菱形的性质以及，利用可得，可得，然后可得，继而可求得的度数．
【详解】解：四边形为菱形，
，，，
，，，
在和中，
，
，
，
，
，
，
．
故选：C．
2．A
【分析】把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．据此即可判断．
【详解】解：A．是中心对称图形，故此选项符合题意；
B．不是中心对称图形，故此选项不合题意；
C．不是中心对称图形，故此选项不合题意；
D．不是中心对称图形，故此选项不合题意；
故选：A．
【点睛】本题主要考查了中心对称图形定义，关键是找出对称中心．
3．B
【详解】试题分析：根据折叠的性质可得∠EBD=∠DBC=29°，再根据矩形的性质即可求得结果.
由题意得∠EBD=∠DBC=29°，
∵矩形ABCD，
∴∠ABC=90°，
∴∠ABE=∠ABC-∠EBD-∠DBC=32°，
故选B.
考点：本题主要考查矩形的性质，折叠的性质
点评：解答本题的关键是熟练掌握矩形的四个角都是直角，折叠前后的图形全等.
4．B
【分析】由菱形的周长可求得AB的长，再利用三角形中位线定理可求得答案0
【详解】∵四边形ABCD为菱形，∴AB28=7，且O为BD的中点．
∵E为AD的中点，∴OE为△ABD的中位线，∴OEAB=3.5．
故选B．
【点睛】本题考查了菱形的性质，由条件确定出OE为△ABD的中位线是解题的关键．
5．A
【分析】由菱形对角线的性质，相互垂直平分即可得出菱形的边长，菱形四边相等即可得出周长．
【详解】由菱形对角线性质知，AO=AC=3，BO=BD=4，且AO⊥BO，
则AB==5，
故这个菱形的周长L=4AB=20．
故选A．
【点睛】本题考查了菱形面积的计算，考查了勾股定理在直角三角形中的运用，考查了菱形各边长相等的性质，本题中根据勾股定理计算AB的长是解题的关键，难度一般．
6．C
【分析】过B′作BD⊥y轴于D，由折叠的性质可得∠B′CP=∠BCP=30°，CB′=BC=4，根据正方形的性质可求出∠OCB′=30°，根据含30°角的直角三角形的性质可得BD′的长，利用勾股定理可求出CD的长，即可求出OD的长，即可得点B′的坐标.
【详解】过B′作B′D⊥y轴于D，
∵四边形OABC是正方形，∠CPB=60°，
∴∠BCP=30°，
∵沿CP折叠正方形，折叠后，点B落在平面内点处，
∴∠B′CP=∠BCP=30°，B′C=BC =4，
∴∠OCB′=30°，
∵B′D⊥y轴，
∴B′D=B′C=2，
∴CD==，
∴OD=OC-CD=4-，
∴点B′的坐标为（2，4-）.
故选C.
【点睛】本题考查了折叠的性质、正方形的性质及含30°角的直角三角形的性质，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等；30°角所对的直角边，等于斜边的一半；熟练掌握折叠的性质是解题关键.
7．A
【分析】根据平行四边形的性质求得，即可求解．
【详解】解：∵四边形是平行四边形，
∴，
∵，
∴，
∴四边形是矩形，
∴选项A最符合题意，
故选：A．
【点睛】本题考查了平行四边形的性质，矩形的判定，掌握“平行四边形的对角相等”是解题的关键．
8．C
【分析】首先连接BE，由题意可得OE为对角线BD的垂直平分线，可得BE=DE，S△BOE=S△DOE=，由三角形的面积则可求得DE的长，得出BE的长，然后由勾股定理求得答案．
【详解】连接BE，如图所示：
由题意可得，OE为对角线BD的垂直平分线，
∴BE＝DE，S△BOE＝S△DOE＝，
∴S△BDE＝2S△BOE＝．
∴DE AB＝，
又∵AB＝2，
∴DE＝，
∴BE＝
在Rt△ABE中，由勾股定理得：AE＝．
故选C．
【点睛】此题考查了矩形的性质、勾股定理以及三角形的面积问题．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
9．C
【分析】由多边形的外角和为，结合每个外角的度数，即可求出n的值，此题得解．
【详解】解：∵一个正n边形的每一个外角都是，
∴，
故选：C．
【点睛】本题考查了多边形的外角和，牢记多边形的外角和为是解题的关键．
10．C
【点睛】本题考查了菱形的性质，勾股定理，熟练掌握菱形的性质是解题的关键；
根据菱形的性质得出、的长，在求出，利用菱形面积等于对角线乘积的一半，也等于，即可得出答案．
【详解】解：∵四边形是菱形，，
∴，，，
在中
∵，
∵，
∴，
∵，
∴．
故选：C．
11．C
【分析】由四边形是正方形和折叠性质得出，，再由三角形的内角和求出．故①正确；由四边形是正方形和折叠性质，判断出四边形是平行四边形，再由，得出四边形是菱形．利用的直角三角形，由勾股定理得出，，得出，故②④正确；由四边形是正方形和折叠性质，得到，所以，故③错误．
【详解】解：由四边形是正方形和折叠性质得出，，
，
故①正确；
由四边形是正方形和折叠性质得出，，，，
，
，
，
又，
，
四边形是平行四边形，
，
四边形是菱形．
在中，，在中，，
，
故②④正确．
由四边形是正方形和折叠性质知，，，，
在和中，
，
，
故③错误．
综上可知，①②④正确．
故选C．
【点睛】本题主要考查了折叠问题，菱形的判定与性质，正方形的性质，全等三角形的判定与性质，勾股定理，解题的关键是掌握图形折叠前后对应边相等、对应角相等．
12．B
【分析】根据A（x，y）在第二象限内可以判断x，y的符号，再根据|x|=2，|y|=3就可以确定点A的坐标，进而确定点A关于原点的对称点的坐标．
【详解】∵A（x，y）在第二象限内，
∴x＜0 y＞0，
又∵|x|=2，|y|=3，
∴x=-2， y=3，
∴点A关于原点的对称点的坐标是（2，-3）．
故选：B．
【点睛】本题考查了关于原点对称的点的坐标，由点所在的象限能判断出坐标的符号，同时考查了关于原点对称的点坐标之间的关系，难度一般．
13．（2,1）
【分析】观察图形，根据中心对称的性质即可解答.
【详解】∵点P（1，1），N（2，0），
∴由图形可知M（3，0），M1（1，2），N1（2，2），P1（3，1），
∵关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分，
∴对称中心的坐标为（2，1），
故答案为（2，1）．
【点睛】本题考查了中心对称的性质：①关于中心对称的两个图形能够完全重合； ②关于中心对称的两个图形，对应点的连线都经过对称中心，并且被对称中心平分．
14．3
【分析】根据四边形为平行四边形可得，根据平行线的性质和角平分线的定义可得出，继而可得，然后根据已知可求得的长度．
【详解】解：∵四边形为平行四边形，
∴，
∴，
∵平分，
∴，
∴，
∴，
∵，
∴．
故答案为：3．
【点睛】本题考查了平行四边形的性质，等腰三角形的判定与性质，解答本题的关键是根据平行线的性质和角平分线的定义得出．
15．5；；；
【分析】根据菱形的四条边都相等求出菱形的边长，再根据邻角互补求出较小的内角为60°，然后判断出较短的对角线与相邻的两边组成等边三角形，再根据等边三角形的性质求出两对角线，然后根据菱形的面积等于对角线乘积的一半列式计算即可得解．
【详解】∵菱形ABCD的周长为20cm，
∴菱形的边长为20÷4=5cm，
∵相邻两内角之比是1:2，
∴较小的内角为180°×=60°，
∴较短的对角线与相邻的两边组成等边三角形，
∴较短的对角线为5cm，
较长的对角线为2×5× =cm，
面积= cm
【点睛】此题考查菱形的性质，解题关键在于求出较小的内角为60°.
16．
【分析】此题考查了中心对称图形的性质，直接利用中心对称图形的性质得出四边形是平行四边形，进而即可得出答案，得出四边形是平行四边形是解题的关键．
【详解】解：∵是的中点，与关于点成中心对称，
∴四边形是平行四边形，
∴，
∴，
故答案为：．
17． 平行 对角线 AC BD 对边 对角
【解析】略
18．（1）见解析 （2）见解析
【分析】（1）由平行四边形的性质得到AB平行CD，得到内错角∠GAO=∠FCH，根据AF＝CE，同时减去EF可得AE=CF，根据SAS可证△ AGE≌△CHF，得到∠AEG=∠CFH，再由邻补角得到内错角相等，得到两线平行；
（2）连接FG、EH ，由（1）可证四边形EGFH是平行四边形即可得到结论．
【详解】在 ABCD中，
∵AB∥CD，
∴∠GAE=∠HCF，
∵AF=CE，
∴AF-EF=CE=EF，
即；AE=CF，
在△AGE与△CHF中，，
∴△AGE≌△CHF（SAS），
∴∠AEG=∠CFH，
∴∠GEO=∠HFO，
∴EG∥FH；
（2）连接FG、EH
由（1）证得△AGE≌△CHF ，EG∥FH，
∴GE=HF，
∴四边形GFHE是平行四边形，
∴GH、EF互相平分．

【点睛】本题考查了平行四边形的性质和判定，全等三角形的判定与性质，注意数形结合，分清平行四边形的性质和判定．
19．(1)见解析
(2)的长度不变，值为
【分析】（1）过点P作于G，过点P作于H，如图1，利用正方形的性质和角平分线的性质证明，进而证明，即可证明．
（2）连接，如图2．证明，得到．再利用正方形的性质和勾股定理求出，即可得到结论．
【详解】（1）证明：过点P作于G，过点P作于H，如图1．
∵四边形是正方形，，
∴．
∴．
∵，即，
∴．
在和中，
，
∴，
∴．
（2）解：的长度不变，值为，理由如下：
连接，如图2．
∵四边形是正方形，
∴，
∵，即，
∴，
∵，即，
∴，
在和中，
，
∴，
∴．
∵四边形是正方形，
∴，
∴．
∴点P在运动过程中，的长度不变，值为．
【点睛】本题主要考查了正方形的性质，勾股定理，角平分线的性质，全等三角形的性质与判定，正确作出辅助线构造全等三角形是解题的关键．
20．(1)，
(2)矩形，见解析
【分析】本题考查矩形，点关于直线对称的知识，解题的关键是掌握点关于直线对称的性质，矩形的判定，即可．
（1）根据点关于直线对称，则，互换即为对称点坐标求出点，根据点关于原点对称横纵坐标互为相反数，即可；
（2）根据点关于原点对称横纵坐标互为相反数，求出点，再根据矩形的判定，即可．
【详解】（1）∵，
∴点关于直线的对称点；
∵关于原点对称横纵坐标互为相反数，
∴关于原点的对称点的坐标为：．
（2）∵点，
∴点原点的对称点的坐标为：，
∵点与点关于原点对称，点与点关于原点对称，
∴，，
∴四边形是平行四边形，
∵点关于直线的对称点为，点关于原点的对称点为，点关于原点的对称点为，
∴，
∴平行四边形是矩形．
21．(1)见解析；
(2)．
【分析】（1）利用平行线的性质，可得，即可求证；
（2）根据三角形中位线的性质，可得，由（1）可得，则
【详解】（1）证明：∵，
∴，
∵为的中点，
∴，
又∵，
∴；
（2）解：∵为的中点，点B为线段的中点，
∴为的中位线，，
∴，
由（1）得，
∴，即，
∴．
【点睛】此题考查了全等三角形的判定与性质，三角形中位线的性质，平行线的性质，解题的关键是熟练掌握相关基础性质．
22．(1)16
(2)见解析
(3)
【分析】（1）点E为AB中点，构造△ABC的中位线EH，2CF＝BC，证△EHG≌△FCG，AG＝3CG，利用等高三角形面积关系和S△AEG＝3依次求△EHG、△GCF、△BGC、△BGA、△BCA的面积，最后求菱形ABCD的面积；
（2）过点F作AB的平行线，交AC的延长线于Q，得到等腰三角形，由三线合一得，结合GHAC，得到AG＝QG，证△AGE≌△QGF，得AE＝QF＝CF；
（3）C′点的轨迹（路径）是G为圆心，半径为的圆，取GF的中点O，OM是△GFC′的中位线，OM，M点的轨迹（路径）是O为圆心，半径为的圆，HM≤OH+OM，HM的最大值是当H、O、M共线时HM＝OH+OM，HM．
【详解】（1）解：如图1，取AC中点H，连接EH，连接BG．
∵点E为AB中点，
∴EH是△ABC的中位线，
∴，EHBC，
∴∠GEH＝∠F，∠EHG＝∠FCG，
∵2CF＝BC，
∴EH＝CF，
∴△EHG≌△FCG（ASA），
∴GH＝GC，
∴AG＝3GH＝3CG，
∵△AEG和△GEH分别选AG和GH为底，高相同，
∴S△AEG＝3S△GEH，
∵S△AEG＝3，
∴S△GEH＝1，
∴S△FCG＝1，
∵2CF＝BC，
∴同理S△BGC＝2S△FGC＝2，S△ABG＝3S△BGC＝6，
∴S△ABC＝8，
∵菱形ABCD中，AB＝AD，CB＝CD，
∴△ABC≌△ADC（SSS），
∴S△ADC＝S△ABC＝8，
∴菱形ABCD的面积是16；
（2）证明：如图2，过点F作AB的平行线，交AC的延长线于Q．
∴∠BAC＝∠Q，
∵AB＝CB，
∴∠BAC＝∠BCA，
∵∠QCF＝∠BCA，
∴∠QCF＝∠Q，
∴CF＝FQ，
∵FH⊥AC于点H，
∴CH＝QHCQ，
∵GHAC，QG＝GH+QH，
∴GQACCQAQ，
∴GQ＝AG，
又∵∠AGE＝∠QGF，∠EAG＝∠Q，
∴△AGE≌△QGF（ASA），
∴AE＝QF，
∴AE＝CF；
（3）解：如图3，
∵GC′＝GC，
∴点C′的轨迹（路径）是G为圆心，半径为的圆，
取GF的中点O，
∵点M为C'F中点，
∴OM是△的中位线，
∴OMGC′，
∴点M的轨迹（路径）是O为圆心，半径为的圆，
∵HM≤OH+OM，
∴HM的最大值是当H、O、M共线时HM＝OH+OM，
∵∠FHG＝90°，GF的中点是O，
∴OHGF，
∵△AGE≌△QGF，
∴GF＝EG＝7，
∴HM的最大值为．
【点睛】本题属于四边形综合题，考查了菱形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题．
23．(1)见解析；
(2)见解析；
【分析】本题主要考查平行四边形的判定和性质，也考查了全等三角形的判定，熟练掌握相关的判定和性质是解答本题的关键．
（1）直接利用两组对边分别平行的四边形是平行四边形证明即可；
（2）先利用平行四边形的性质得到，，继而得到，从而得证；
【详解】（1）∵平行四边形，
，
又，
∴四边形是平行四边形；
（2）∵平行四边形，
，，，
又∵四边形是平行四边形，
，
，
，
24．（1）证明见解析；（2）AM=1．理由见解析．
【详解】解：（1）∵四边形ABCD是菱形，∴ND∥AM，
∴∠NDE=∠MAE，∠DNE=∠AME，
∵点E是AD中点，∴DE=AE，
在△NDE和△MAE中，，
∴△NDE≌△MAE（AAS），∴ND=MA，
∴四边形AMDN是平行四边形；
（2）解：当AM=1时，四边形AMDN是矩形．
理由如下：
∵四边形ABCD是菱形，∴AD=AB=2，
∵平行四边形AMDN是矩形，∴DM⊥AB，即∠DMA=90°，
∵∠DAB=60°，∴∠ADM=30°，
∴AM=AD=1．
【点睛】本题考查矩形的判定；平行四边形的判定；菱形的性质．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)