2.1多边形同步练习（含解析）

中小学教育资源及组卷应用平台
2.1多边形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．某学生在计算四个多边形的内角和时，得到下列四个答案，其中错误的是（　　）
A． B． C． D．
2．窗棂是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案．如图是从某窗棂样式结构图案上摘取的部分．已知，则的度数是（　　）
A． B． C． D．
3．小聪为某机器人编制一段程序，如果机器人以的速度在平地上按照图中的步骤行走，那么该机器人从开始到停止所需的时间为（ ）
A． B． C． D．
4．用边长相等的下列两种正多边形，不能进行平面镶嵌的是（ ）
A．等边三角形和正六边形 B．正方形和正八边形
C．正五边形和正十边形 D．正六边形和正十二边形
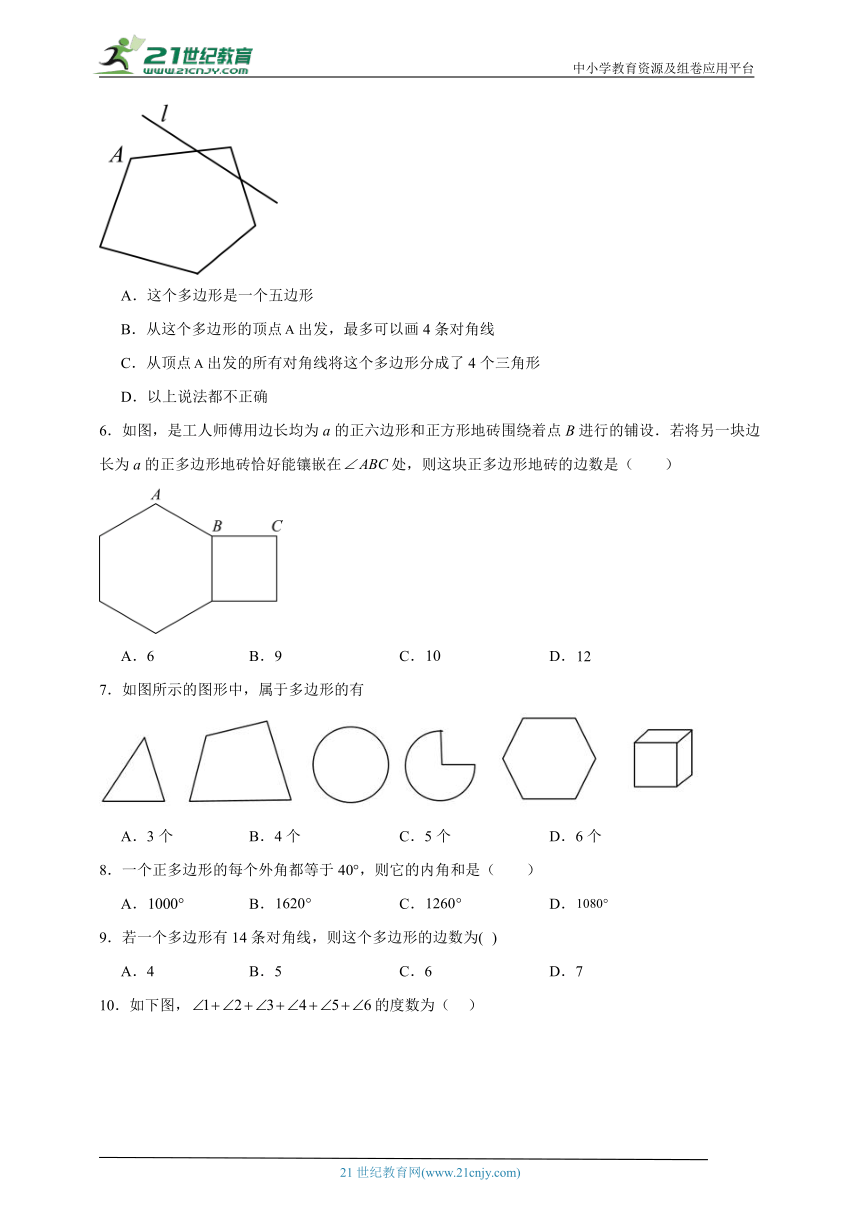
5．在学习完多边形后，小华同学将一个五边形沿如图所示的直线剪掉一个角后，得到一个多边形，下列说法正确的是（ ）
A．这个多边形是一个五边形
B．从这个多边形的顶点出发，最多可以画4条对角线
C．从顶点出发的所有对角线将这个多边形分成了4个三角形
D．以上说法都不正确
6．如图，是工人师傅用边长均为a的正六边形和正方形地砖围绕着点B进行的铺设．若将另一块边长为a的正多边形地砖恰好能镶嵌在处，则这块正多边形地砖的边数是（　　）

A．6 B．9 C． D．
7．如图所示的图形中，属于多边形的有
A．3个 B．4个 C．5个 D．6个
8．一个正多边形的每个外角都等于40°，则它的内角和是（　　）
A． B． C． D．
9．若一个多边形有14条对角线，则这个多边形的边数为( )
A．4 B．5 C．6 D．7
10．如下图，的度数为（ ）
A．540° B．500° C．460° D．420°
11．为了让居民有更多休闲和娱乐的地方，政府又新建了几处广场，工人师傅在铺设地面时，准备选用同一种正多边形地砖．现有下面几种形状的正多边形地砖，其中不能进行平面镶嵌的是　　　　　　　　　　　　　　（ ）
A．正三角形 B．正方形 C．正五边形 D．正六边形
12．如图所示，在锐角中，、分别是、边上的高，且、交于点，若，则的度数是(　　)
A．108° B．128° C．138° D．158°
二、填空题
13．如图，在边长为的大正方形中，剪去一个边长为的小正方形，然后将余下的部分剪开拼成如图所示的长方形，若记大正方形的周长为，拼成的长方形的周长为，则与的大小关系是 ．
14．过某个多边形的一个顶点的所有对角线，将这个多边形分成2023个三角形，则这个多边形的边数为 ．
15．如图1，图2，图3，在中，分别以、为边，向外作正三角形，正四边形，正五边形，、相交于点O．
（1）如图1， ：如图2， ；如图3， ；
（2）如图4，已知：、是以为边向外所作正n边形的一组邻边；、是以为边向外所作正n边形的一组邻边．、的延长线交于点O．此时， （用含n的式子表示）．
16．如图，在△ACD与△BCE中，AD与BE相交于点P，若AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，则∠APB的度数为 ．

17．用等边三角形和正方形作平面镶嵌，则在它的每个顶点周围有个等边三角形和 个正方形．
三、解答题
18．如图所示，试说明．

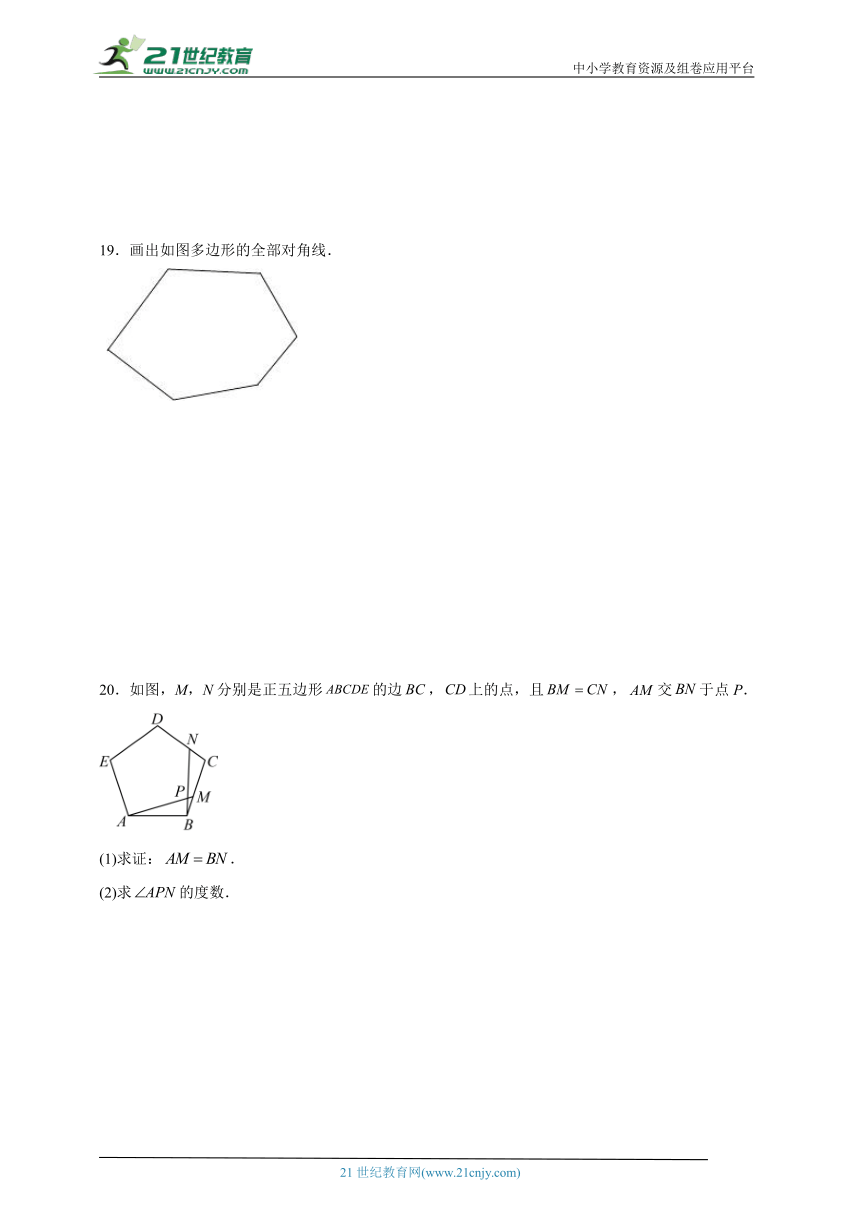
19．画出如图多边形的全部对角线．
20．如图，M，N分别是正五边形的边，上的点，且，交于点P．

(1)求证：．
(2)求的度数．
21．一个多边形的各内角都等于120°，它是几边形？
22．若n边形的内角和等于它外角和的3倍，求边数n.
23．如图，在五边形ABCDE中，，EF平分，CF平分，若，求的度数．
24．如图，每个小正方形的边长都为1．
(1)四边形的面积________；
(2)四边形的周长________；
(3)与有什么关系？请说明理由．
《2.1多边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B D C D A C D D
题号 11 12
答案 C B
1．C
【分析】本题主要考查了多边形的内角和定理，对于定理的理解是解决本题的关键．
n边形的内角和是，即多边形的内角和一定是180的正整数倍，依此即可解答．
【详解】解：多边形的内角和公式是，
内角和是时候是三角形；
内角和是时候是五边形；
内角和是的时候是十边形，
内角和是时候算出来的边数不是整数，所以错误的是C，
故选：C．
2．B
【分析】先根据平行线的性质即可得到，再根据多边形的外角和是即可求得结果．
【详解】解：∵
∴
∴的外角为:
∵五边形的外角和为，
∴．
故选：．
【点睛】本题考查了平行线的性质，多边形的外角和定理，熟记多边形的外角和为是解题的关键．
3．B
【分析】先判断出机器人所走过的路线是正多边形，然后用多边形的外角和除以每一个外角的度数求出多边形的边数，再根据周长公式列式进行计算即可得解﹒
【详解】解∶根据题意得，机器人所走过的路线是正多边形，
∵每一次都是左转，
∴多边形的边数为：，
∴周长为6×2=12米．
∴该机器人从开始到停止所需的时间为：﹒
故选：B﹒
【点睛】本题考查了多边形的内角与外角，判断出走过的路线是正多边形是解题的关键．
4．D
【分析】分别求出各个正多边形每个内角的度数，再结合镶嵌的条件即可作出判断．
【详解】A、正三角形的每个内角是60°，正六边形的每个内角是120°，∵2×60°+2×120°=360°，能密铺；
B、正八边形的每个内角是135°，正方形的每个内角是90°，∵2×135°+90°=360°，能密铺，；
C、正五形的每个内角是108°，正十边形的每个内角是144°，∵2×108°+144°=360°，能密铺，；
D、正六边形的每个内角是120°和正十二边形的每个内角是150°，120m+150n=360°，m=3﹣n，显然n取任何正整数时，m不能得正整数，故不能铺满．
故选D．
【点睛】本题考查平面镶嵌（密铺），关键是掌握平面镶嵌（密铺）的条件.
5．C
【分析】本题考查了多边形的对角线个数问题及被对角线分割成的三角形数目问题，解题关键是找出其中的规律．根据选项一一对照判断即可．
【详解】解：A、这个多边形是一个六边形，故错误，不符合题意．
B、从这个多边形的顶点出发，最多可以画3条对角线，故错误，不符合题意，
C、从顶点出发的所有对角线将这个多边形分成了4个三角形，正确，符合题意，
D、以上说法C正确．
故选∶C．
6．D
【分析】本题考查了正多边形的内角和．熟练掌握正边形的内角和为是解题的关键．
由题意知，正六边形的内角为，正方形的内角为，则，设镶嵌在处的正多边形地砖的边数为，依题意得，，计算求解即可．
【详解】解：由题意知，正六边形的内角为，正方形的内角为，
∴，
设镶嵌在处的正多边形地砖的边数为，
依题意得，，
解得，
故选：D．
7．A
【详解】解：根据多边形的定义：平面内不在同一条直线上的几条线段首尾顺次相接组成的图形叫多边形．显然只有第一个、第二个、第五个符合题意．
故选A．
8．C
【分析】先根据多边形的外角和求多边形的边数，再根据多边形的内角和公式求出即可．
【详解】解：设这个多边形是n边形，根据多边形的外角和为360°可得，40°×n=360°，
解得n=9．
所以这个多边形的内角和为（9-2）×180°=1260°．
故选C.
【点睛】本题考查了多边形的内角与外角，能正确求出多边形的边数是解此题的关键，注意：多边形的外角和等于360°，边数为n的多边形的内角和=(n 2)×180°.
9．D
【分析】根据多边形的对角线公式进行计算即可得解．
【详解】n边形共有条对角线.
当n＝4时， =2；
当n＝5时， =5；
当n＝6时， =9；
当n＝7时， =14.
故选D．
【点睛】本题考查多边形的对角线，关键是熟记多边形的对角线公式.
10．D
【分析】根据三角形内角和定理可得，根据平角的定义和四边形内角和可得，同理可得，据此即可求解．
【详解】解：如图所示，
∵，
∴，
∵，，
∴
∵
∴，
同理可得：，
∴，
故选：D．
【点睛】本题考查了三角形内角和定理，四边形内角和定理，熟知四边形内角和等于是解题的关键．
11．C
【分析】本题意在考查学生对平面镶嵌知识的掌握情况，体现了学数学用数学的思想，由平面镶嵌的知识可知只用一种正多边形能够铺满地面的是正三角形或正四边形或正六边形．
【详解】解：A、正三角形的每个内角是，能整除，能镶嵌；
B、正方形的每个内角是，能整除，能镶嵌；
C、正五边形每个内角是，不能整除，不能镶嵌；
D、正六边形的每个内角是，能整除，能镶嵌．
故选：C．
12．B
【分析】先根据四边形的内角和公式可求出的度数，再根据对顶角相等即可得出答案．
【详解】由题意得：
在四边形ADFE中，
即
解得：
则
故选：B．
【点睛】本题考查了四边形的内角和公式、对顶角的性质（对顶角相等），根据内角和公式求出的度数是解题关键．
13．
【分析】根据周长公式进行计算即可．
【详解】解：左图的周，右图的周长，
所以，
故答案为：．
【点睛】本题考查计算图形周长，理解周长的定义以及长方形周长的计算方法是正确解答的前提．
14．2025
【分析】根据多边形的边数=三角形的个数+2，即可求解．
【详解】解：∵过某个多边形的一个顶点的所有对角线，将这个多边形分成2023个三角形，
∴这个多边形的边数为，
故答案为：2025．
【点睛】本题主要考查多边形的边数，理解多边形和三角形之间的联系是解题的关键．过n边形的一个顶点的所有对角线，将这个多边形分成个三角形．
15．
【分析】（1）根据等边三角形的性质可以得出△ABE≌△ADC，根据三角形的外角与内角的关系就可以求出∠BOC的值；
在图2中，连接BD，然后用同样的方法证明△DAC≌△BAE，根据三角形外角与内角之间的关系就可以求出∠BOC的值；
依此类推就可以得出当作五边形的时候就可以求出图3中∠BOC的值；
（2）根据图1中，∠BOC=120°=；图2中，∠BOC=90°=；图3中，∠BOC=72°=；以此类推找出规律，即可得出图4中当作正n边形时，∠BOC=．
【详解】（1）解：如图1，
∵△ABD和△AEC是等边三角形，
∴AD=AB，AE=AC，∠DAB=∠EAC=∠ABD=∠ADB=60°，
∴∠DAB+∠BAC=∠EAC+∠BAC，
即∠DAC=∠BAE．
在△ABE和△ADC中，
，
∴△ABE≌△ADC（SAS），
∴∠CDA=∠EBA，
∵∠BOC=∠BDO+∠OBD，
∴∠BOC=∠BDA+∠ABE+∠OBD，
∴∠BOC=∠BDA+∠ADC+∠OBA，
∴∠BOC=∠BDA+∠OBD=60°+60°=120°；
如图2中，连接BD，
∵四边形ABFD和四边形ACGE是正方形，
∴AB=AD，AE=AC，∠BAD=∠CAE=90°，∠BDA=∠DBA=45°，
∴∠BAD+∠DAE=∠CAE+∠DAE，
即∠BAE=∠CAD，
在△ABE和△ADC中，
，
∴△ABE≌△ADC（SAS），
∴∠ABE=∠ADC，
∵∠BOC=∠BDO+∠DBO，
∴∠BOC=∠BDA+∠ADO+∠DBO，
∴∠BOC=∠BDA+∠ABE+∠DBO，
∴∠BOC=∠BDA+∠DBA=45°+45°=90°；
如图3中，连接BD，
∵五边形ABHFD和五边形ACIGO是正五边形，
∴AB=AD，AE=AC，∠BAD=∠EAC=108°，
∴∠BAD+∠DAE=∠EAC+∠DAE，∠ABD=∠ADB=36°，
∴∠BAE=∠DAC，
在△ABE和△ADC中，
，
∴△ABE≌△ADC（SAS），
∴∠ABE=∠ADC，
∵∠BOC=∠OBD+∠BDO，
∴∠BOC=∠ADB+∠ADC+∠OBD，
∴∠BOC=∠ADB+∠ABE+∠OBD，
∴∠BOC=∠ADB+∠ABD=72°．
故答案为：120°，90°，72°；
（2）由题可得，
图1中，∠BOC=120°=；
图2中，∠BOC=90°=；
图3中，∠BOC=72°=；
以此类推，图4中，当作正n边形时，∠BOC=．
故答案为：．
【点睛】本题属于三角形综合题，主要考查了全等三角形的判定与性质、等边三角形、正四边形等图形的性质，解决问题的关键是利用正n边形各边相等证明两个三角形全等，运用了类比的思想方法，同时还要熟练掌握正n边形每一个内角的求法，并根据三角形的一个外角等于与它不相邻的两个内角和得出结论．
16．50°/50度
【分析】易证△ACD≌△BCE，由全等三角形的性质可知：∠A＝∠B，再根据已知条件和四边形的内角和为360°，即可求出∠BPD的度数，利用邻补角求得∠APB的度数．
【详解】在△ACD和△BCE中，
，
∴△ACD≌△BCE（SSS），
∴∠A＝∠B，∠BCE＝∠ACD，
∴∠BCA＝∠ECD，
∵∠ACE＝55°，∠BCD＝155°，
∴∠BCA+∠ECD＝100°，
∴∠BCA＝∠ECD＝50°，
∵∠ACE＝55°，
∴∠ACD＝105°
∴∠A+∠D＝75°，
∴∠B+∠D＝75°，
∵∠BCD＝155°，
∴∠BPD＝360°﹣75°﹣155°＝130°，
∴∠APB＝180°－∠BPD＝50°
故答案为：50°．
【点睛】本题考查了全等三角形的判定和性质、三角形的内角和定理以及四边形的内角和定理，解题的关键是利用整体的数学思想求出∠B+∠D＝75°．
17．
【分析】根据正多边形的组合能镶嵌成平面的条件可知，位于同一顶点处的几个角之和为如果设用个正三角形，个正四边形，则有，求出此方程的正整数解即可．
【详解】解：设用个正三角形，个正四边形能进行平面镶嵌．
由题意，有，
解得，
当时，．
故在它的每个顶点周围，有个正三角形和个正方形．
故答案为：．
【点睛】本题考查了平面镶嵌密铺几何图形镶嵌成平面的关键是：围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角．
18．见解析
【分析】本题考查了多边形内角和，及三角形的一个外角等于与它不相邻的两个内角的和的性质，熟记性质并准确识图是解题的关键；
连接，根据三角形的一个外角等于与它不相邻的两个内角的和，把所求角转化为同一个多边形内，根据多边形内角和定理即可解答．
【详解】证明：连接，
，
．
19．图形见解析
【详解】分析：此图为6边形，有=9条对角线，依次画出即可．
本题解析：
如图所示：
20．(1)见解析
(2)
【分析】（1）利用证明即可得出结论；
（2）求出，由全等形的性质可得，然后根据三角形外角的性质即可求解；
【详解】（1）证明：多边形是正五边形，
，，
在和中，，
，
；
（2）解：多边形是正五边形，
，
，
，
是的外角，
．
【点睛】本题考查了正五边形的性质，三角形全等的判定和性质，三角形外角的性质，证明是解题的关键．
21．六边形
【分析】设这个多边形的边数为n，根据多边形的内角和公式列出方程，解方程求解即可．
【详解】解：设这个多边形的边数为n，
则(n－2)×180°＝n×120°，
解得n＝6.
所以它是六边形．
【点睛】本题考查多边形的内角和．熟练掌握多边形的内角和公式是解题的关键．
22．n=8.
【分析】根据n边形的内角和等于外角和的3倍，可得方程180(n﹣2)＝360×3，再解方程即可.
【详解】解：由题意得：180(n﹣2)＝360×3，
解得：n＝8，
【点睛】本题考查了多边形内角和与外角和，要结合多边形的内角和公式与外角和的关系来寻求等量关系，构建方程即可求解．
23．135°
【分析】根据角平分线的性质，，，再根据五边形内角和求出的值，可得到的值，再利用四边形内角和为360°即可求出的度数．
【详解】解：∵EF平分，CF平分，
∴，．
∵，
∴．
∵五边形的内角和为（5-2）×180°=540°，，
∴，
即，
∵四边形EFBD内角和为360°，
∴．
【点睛】本题考查了角平分线和多边形内角和，能熟练运用角平分线与多边形内角和求角的度数是解题的关键．
24．(1)12
(2)
(3)相等，且垂直
【分析】（1）根据正方形的面积减去三个直角三角形的面积计算即可；
（2）根据勾股定理计算即可；
（3）先根据勾股定理的逆定理确定是直角三角形，可得答案．
【详解】（1）四边形的面积；
故答案为：12；
（2）四边形的周长为
；
故答案为：；
（3）相等，且垂直．
理由：如图所示，连接．
根据勾股定理，得，
∴，
∴是直角三角形，
∴，
所以，且．
【点睛】本题主要考查了勾股定理在网格中的应用，勾股定理逆定理，求不规则图形的面积等，将不规则图形的面积转化为规则图形的面积的和或差是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)