4.5一次函数的应用同步练习（含解析）

中小学教育资源及组卷应用平台
4.5一次函数的应用
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．乐乐超市购进一批拼装玩具，进价为每个15元，在销售过程中发现，日销售量（个）与销售单价（元）之间满足如图所示的一次函数关系，若该玩具某天的销售单价是20元时，则当日的销售利润为（ ）
A．200元 B．300元 C．350元 D．500元
2．如图，已知直线与直线都经过，直线交y轴于点，交x轴于点A，直线交y轴于点D，P为y轴上任意一点，连接，以下说法错误的是（　　）
A．的面积为 3 B．当的值最小时，点P的坐标为
C．为直角三角形 D．方程组的解为
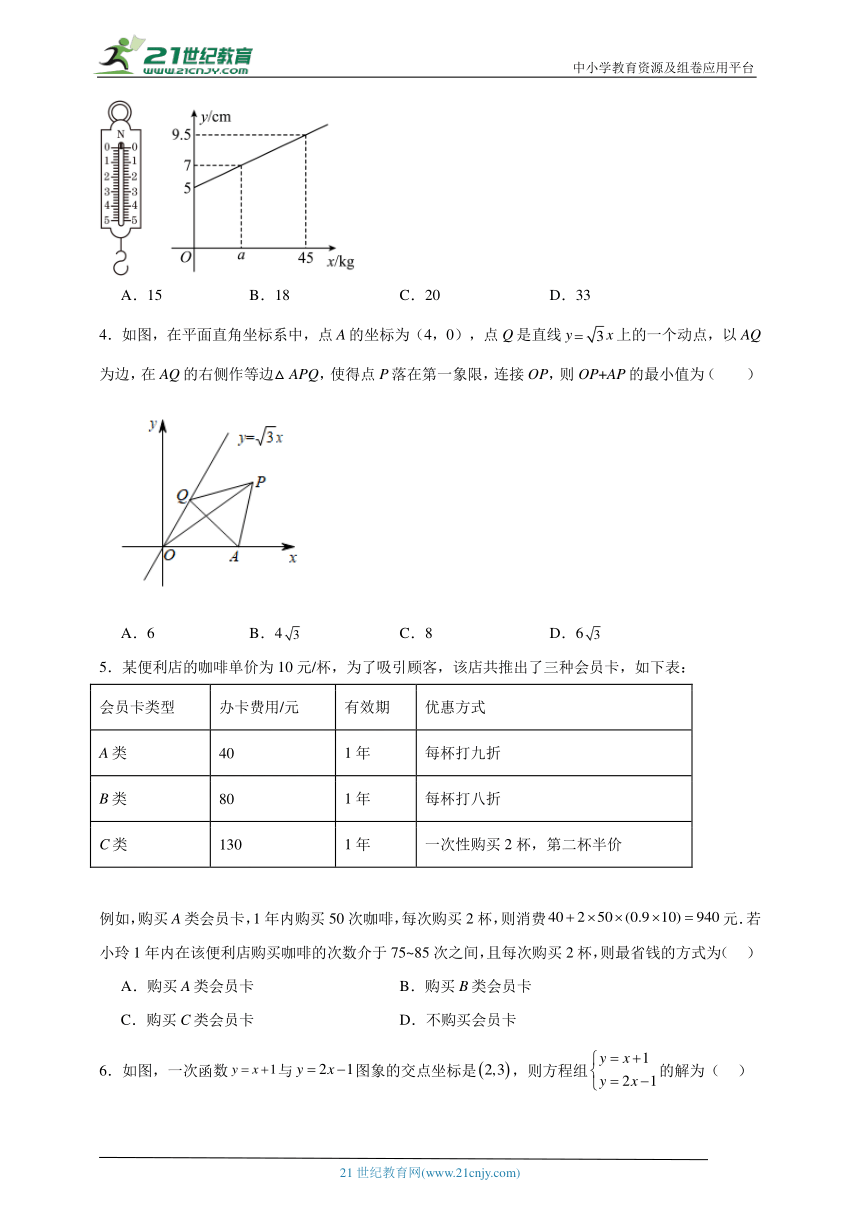
3．如图，一个条形测力计不挂重物时长5cm，挂上重物后，在弹性限度内弹簧伸长的长度与所挂重物的质量成正比，弹簧总长y（cm）关于所挂物体质量x（kg）的函数图象如图所示，则图中a的值是（　　）
A．15 B．18 C．20 D．33
4．如图，在平面直角坐标系中，点A的坐标为（4，0），点Q是直线yx上的一个动点，以AQ为边，在AQ的右侧作等边△APQ，使得点P落在第一象限，连接OP，则OP+AP的最小值为（　　）
A．6 B．4 C．8 D．6
5．某便利店的咖啡单价为10元/杯，为了吸引顾客，该店共推出了三种会员卡，如下表：
会员卡类型 办卡费用/元 有效期 优惠方式
A类 40 1年 每杯打九折
B类 80 1年 每杯打八折
C类 130 1年 一次性购买2杯，第二杯半价
例如，购买A类会员卡，1年内购买50次咖啡，每次购买2杯，则消费元．若小玲1年内在该便利店购买咖啡的次数介于75~85次之间，且每次购买2杯，则最省钱的方式为（ ）
A．购买A类会员卡 B．购买B类会员卡
C．购买C类会员卡 D．不购买会员卡
6．如图，一次函数与图象的交点坐标是，则方程组的解为（ ）
A． B． C． D．
7．如图，直线与两坐标轴分别交于，两点，点是的中点，点，分别是直线，轴上的动点，则的周长的最小值是( )
A． B． C． D．
8．如图所示，一次函数的图象经过点，则方程的解是（ ）
A． B． C． D．无法确定
9．已知方程的解是，则函数的图象可能是（ ）
A． B．
C． D．
10．水龙头关闭不严会造成滴水，为了调查滴水量与流水时间的关系，进行以下试验，并记录如表：
流水时间t/分钟 1 2 4 7
滴水量w/毫升 16 19 a 34
已知滴水量w与流水时间t之间为一次函数关系，以上记录的数据中a的值是（　　）
A．22 B．23 C．24 D．25
11．如图，在平面直角坐标系中，已知A（5，0）点P为线段OA上任意一点．在直线y＝x上取点E，使PO＝PE，延长PE到点F，使PA＝PF，分别取OE、AF中点M、N，连结MN，则MN的最小值是（　　）

A．2.5 B．2.4 C．2.8 D．3
12．如果点同时在函数与的图象上，那么，的值分别为（ ）
A．a=-3，b=-1 B．a=-3，b=1
C．a=1，b=-3 D．a=-1，b=3
二、填空题
13．如图，一次函数y=﹣x﹣2与y=2x+m的图象相交于点P（n，﹣4），则关于x的不等式组的解集为 ．

14．如图，已知一次函数，当x 时，；
当x 时，；
当x 时，；
当时，x的取值范围是 ．
15．今年清明节期间，为提倡文明、环保祭祖，某烟花销售商拟今年不再销售烟花爆竹，改为销售鲜花．经过市场调查，发现有甲、乙、丙、丁四种鲜花组合比较受顾客的喜爱，于是制定了进货方案，其中甲、丙的进货量相同，乙、丁的进货量相同；甲与丁单价均20元/束，乙、丙的单价均为40元/束，且甲、乙的进货总价比丙、丁的进货总价多560元．由于年末资金周转紧张，所以临时决定只购进甲、乙两种组合，甲、乙的进货量与原方案相同，且甲、乙的进货总量不超过400束，则该销售商最多需要准备 元进货资金．
16．（1）一次函数的图像上，位于x轴上方的点的横坐标的范围是 ．
（2）当时，直线在x轴的上方，则不等式的解集是 ．
17．如图，平面直角坐标系中，已知直线上一点 ，为轴上一点，连接，以为边做等腰直角三角形，，过点作线段轴，垂足为，直线与直线交于点，且，连接，直线与直线交于点，则点的坐标是

三、解答题
18．一个弹簧不挂重物时长，挂上重物后伸长的长度与所挂重物的质量成正比，如果挂上的物体后，弹簧伸长．求弹簧总长y（单位：）关于所挂物体质量x（单位：）的函数解析式．
19．某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费，月用水量不超过20立方米时，按2元/立方米计费；月用水量超过20立方米时，其中的20立方米仍按2元/立方米收费，超过部分按2.6元/立方米计费．设每户家庭用水量为x立方米时，应交水费y元．
（1）当0≤x≤20时，y与x的函数关系式为 ；
当x＞20时，y与x的函数关系式为 ．
（2）小明家第二季度交纳水费的情况如下：
月份 四月份 五月份 六月份
交费金额 30元 34元 47.8元
小明家这个季度共用水多少立方米？
20．如图，在平面直角坐标系中，直线 过点．若直线 与x轴、y轴分别交于点B、D，且与直线交于点C，点C的横坐标为2．
(1)求直线的表达式；
(2)直线 上是否存在点M，使为等腰直角三角形？若存在，请求出所有满足条件的点M的坐标；若不存在，请说明理由．
21．某校为实施国家“营养早餐”工程，食堂用甲、乙两种原料配制成某种营养食品，已知这两种原料的维生素C含量及购买这两种原料的价格如下表：
现要配制这种营养食品20千克，要求每千克至少含有480单位的维生素C．设购买甲种原料x千克．
(1)至少需要购买甲种原料多少千克
(2)设食堂用于购买这两种原料的总费用为y元，求y与x的函数关系式．并说明购买甲种原料多少千克时，总费用最少
22．已知函数和相交于点．
（1）求k、b的值；
（2）在同一坐标系中画出两个函数的图象，利用图象求当x取何值时有：①；②且．
23．某饮料厂生产一种饮料，经测算，用1吨水生产的饮料所获利润（元）是1吨水的买入价（元）的一次函数．根据下表提供的数据，求关于的函数表达式．当水价为每吨元时，吨水生产的饮料所获的利润是多少？
1吨水的买入价（元）
利润（元）
24．如图，在平面直角坐标系中，点在y轴正半轴上，点在x轴正半轴上，且．．
(1)求AB；
(2)在y轴上是否存在一点P，使得最小？若存在，请求出的最小值；
(3)在x轴上是否存在一点M，使是以AB为腰的等腰三角形？若存在，请直接写出M点坐标．
《4.5一次函数的应用》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B B C C C D B C C D
题号 11 12
答案 B D
1．B
【分析】根据题意，利用待定系数法求出与的一次函数关系式，然后将代入即可求出销售量，最后利用销售收入减去成本支出即可求出销售利润．
【详解】解：设与的一次函数关系式为，
由图可得，
解得，
所以与的一次函数关系式为，
把代入可得，
所以销售利润为（元）．
故选B．
【点睛】本题考查求一次函数的关系式和利润问题，熟练掌握待定系数法求一次函数的关系式是解题的关键．
2．B
【分析】求得和的长，根据三角形面积计算公式，即可得到的面积；根据轴对称的性质以及两点之间，线段最短，即可得到当的值最小时，点P的坐标为；利用勾股定理的逆定理进行判断；根据一次函数图象与二元一次方程的关系，利用交点坐标可得方程组的解．
【详解】A、把，代入直线，
可得，解得，
∴直线，
令，则，
∴，
∴．
把代入直线，
可得，解得，
∴直线，
令，则，
∴，
∴，
∴，
故本选项正确，不符合题意；
B、点A关于y轴对称的点为，
由点C、的坐标得，直线的表达式为：，
令，则，
∴当的值最小时，点P的坐标为，
故本选项错误，符合题意；
C、∵，，，
∴，，，
∴，
∴为直角三角形，
故本选项正确，不符合题意；
D、∵直线与直线都经过，
∴方程组的解为，
故本选项正确，不符合题意．
故选：B．
【点睛】本题考查了一次函数与二元一次方程组，一次函数的图象与性质，勾股定理，三角形的面积以及轴对称---最短路线问题，凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，多数情况要作点关于某直线的对称点．
3．C
【分析】根据待定系数法可以求出y与x的函数关系式，然后将y=7代入函数解析式，即可得到a的值．
【详解】解：设y与x的函数关系式为y=kx+b，
∵该函数过点（0，5），（45，9.5），
∴，
解得，
即y与x的函数关系式为y=0.1x+5，
当y=7时，
7=0.1x+5，
解得x=20，
∴a=20，
故选：C．
【点睛】本题考查了一次函数的应用，解答本题的关键是会用待定系数法求一次函数的解析式，题目中用的数学思想是数形结合的思想．
4．C
【分析】根据点Q的运动先证明点P在直线PM是运动，再根据轴对称最值问题，作点P关于直线PM的对称点B，连接AB，求出AB的长即可．
【详解】解：如图，作∠OAM＝60°，边AM交直线OQ于点M，作直线PM，
由直线yx可知，∠MOA＝60°，
∴∠MOA＝∠OAM＝60°，
∴△OAM是等边三角形，
∴OA＝OM，
∵△APQ是等边三角形，
∴AQ＝AP，∠PAQ＝60°，
∴∠OAQ＝∠MAP，
∴△OAQ≌△MAP（SAS），
∴∠QOA＝∠PMA＝60°＝∠MAO，
∴PM∥x轴，即点P在直线PM上运动，
过点O关于直线PM的对称点B，连接AB，AB即为所求最小值，
此时，在Rt△OAB中，OA＝4，∠BAO＝60°，
∴∠OBA＝30°，
∴AB＝2OA＝8．
故选：C．
【点睛】本题属于一次函数与几何综合题，涉及勾股定理，等边三角形的性质与判定，全等三角形的性质与判定，轴对称最值问题，旋转的性质等知识，解题的关键是得出点P在直线PM是运动．
5．C
【分析】设一年内在该便利店买咖啡的次数为x次，消费的钱数为y元，根据题意得：列出3类会员卡用含x的关系表示消费的费用y，再确定y的范围，进行比较即可解答．
【详解】设一年内在该便利店买咖啡的次数为x次，消费的钱数为y元，根据题意得：yA=40+0.9x=40+18x，yB=80+0.8x=80+16x，yC=130+15=130+15x，
当75≤x≤85时,
1390≤yA≤1570；
1280≤yB≤1440；
1255≤yC≤1405；
由此可见，C类会员年卡消费最低，所以最省钱的方式为购买C类会员年卡．
故选：C．
【点睛】本题考查了一次函数的应用，解决本题的关键是根据题意，列出函数关系式，并确定函数值的范围．
6．D
【分析】根据“从图形的角度看，确定两条直线交点的坐标，相当于求相应的二元一次方程组的解”即可得出结论．
【详解】解：∵一次函数y＝x＋1与y＝2x 1图象的交点是（2，3），
∴方程组的解为．
故选：D．
【点睛】此题主要考查了图象法解二元一次方程组，掌握二元一次方程组的解与相应的两个函数图象的交点坐标之间的关系是解题的关键．
7．B
【分析】本题考查轴对称最短路线问题，勾股定理，坐标与图形，解题的关键是利用对称性在找到周长的最小时点、点位置，凡是涉及最短距离的问题，一般要考虑线段的性质定理，多数情况要作点关于某直线的对称点．作点关于的对称点，关于的对称点，连接，，由轴对称的性质，可得，，故当点，，，在同一直线上时，的周长，此时周长最小，依据勾股定理即可得到的长，进而得到周长的最小值．
【详解】解：如图，作点关于的对称点，关于的对称点，连接分别交、于点、，此时三角形的周长最小，
∵直线与两坐标轴分别交于、两点，
∴，，
∴，
∴，
由轴对称的性质，可得，，，，，
∴，
∴是等腰直角三角形，
∵点是的中点，
∴，
∴，，
∴，
的周长，此时周长最小，
在中，，
故选：B．
8．C
【分析】将点代入直线解析式，然后与方程对比即可得出方程的解．
【详解】解：一次函数的图象经过点，
∴，
∴为方程的解，
故选：C．
【点睛】题目主要考查一次函数与一元一次方程的联系，理解二者联系是解题关键．
9．C
【分析】由于方程的解是，即时，，所以直线经过点，然后对各选项进行判断．
【详解】解：方程的解是，
经过点．
故选：C．
【点睛】本题考查了一次函数与一元一次方程：已知一次函数的函数值求对应的自变量的值的问题就是一元一次方程的问题．
10．D
【分析】先利用待定系数法求出该一次函数表达式，再将t＝4代入计算即可．
【详解】解：设该一次函数表达式为w＝kt+b（k≠0），根据题意得：
，解得 ，
∴该一次函数表达式为w＝3t+13，
当t＝4时，a＝3×4+13＝25．
故选D．
【点睛】本题主要考查了一次函数的应用，利用待定系数法求出一次函数的解析式是解答本题的关键．
11．B
【分析】如图，连接PM，PN，设AF交EM于J，连接PJ．证明四边形PMJN是矩形，推出MN=PJ，求出PJ的最小值即可解决问题．
【详解】解：如图，连接PM，PN，设AF交EM于J，连接PJ．

∵PO=PE，OM=ME，
∴PM⊥OE，∠OPM=∠EPM，
∵PF=PA，NF=NA，
∴PN⊥AF，∠APN=∠FPN，
∴∠MPN=∠EPM+∠FPN=（∠OPF+∠FPA）=90°，∠PMJ=∠PNJ=90°，
∴四边形PMJN是矩形，
∴MN=PJ，
∴当JP⊥OA时，PJ的值最小此时MN的值最小，
∵AF⊥OM，A（5，0），直线OM的解析式为y=x
∴设直线AF的解析式为y=x+b
∵直线AF过A（5，0），
∴=0，
∴b=，
∴y=，
由，解得
∴
∴PJ的最小值为=2.4
即MN的最小值为2.4
故选：B．
【点睛】本题考查一次函数的应用，矩形的判定和性质，垂线段最短等知识，解题的关键是学会用转化的思想思考问题，属于中考选择题中的压轴题．
12．D
【分析】把点代入两个函数解析式得到方程组 然后解方程组即可．
【详解】把点(1,2)代入y=ax+b与中得
解方程组得
故选D.
【点睛】考查一次函数的交点问题，把点代入两个函数解析式，组成方程组是解题的关键.
13．﹣2＜x＜2
【分析】先将点P（n，﹣4）代入y=﹣x﹣2，求出n的值，再找出直线y=2x+m落在y=﹣x﹣2的下方且都在x轴下方的部分对应的自变量的取值范围即可．
【详解】∵一次函数y=﹣x﹣2的图象过点P（n，﹣4），
∴﹣4=﹣n﹣2，解得n=2，
∴P（2，﹣4），
又∵y=﹣x﹣2与x轴的交点是（﹣2，0），
∴关于x的不等式组的解集为
故答案为
【点睛】本题考查了一次函数与一元一次不等式，体现了数形结合的思想方法，准确确定出n的值，是解答本题的关键．
14．
【分析】根据函数图像上即可求解．
【详解】
，即，解得
故答案为．
即，在直线下方所有的横坐标点的集合
故答案为．
即，在直线上方所有的横坐标点的集合
故答案为．
即，在直线之间所有的横坐标点的集合
故答案为．
【点睛】本题考查了一次函数图像与一元一次不等式，熟练掌握上述知识点是解答本题的关键．
15．12280
【分析】一是甲、乙、丙、丁四种鲜花求进价时都满足：总价=单价×数量关系式；二是甲乙的总价丙丁的总价=560元；三是甲、乙的进货量数量关系为；四是销售商货资金表示为，综合用不等式的知识结合函数知识可求进货最多资金．
【详解】解：设甲、丙进货量各为x束，乙丁进货量各为y束；甲、丁单价为20元/束， 乙、丙单价为40元/束，
依题意得： ，
化简得：， 即，
∵年末只购进甲、乙两种组合，且进货量不变，总数不超过400束，
∴，
∴，
解得：，
设进货总资金为w元，则有：，
当时，的最大值为，
∴该销售商最多需要准备12280元进货资金．
故答案为12280．
【点睛】本题考查一元一次不等式的应用，二元一次方程的应用，一次函数的应用，重点掌握总价、数量和单价之间的等量关系，进货总数不超过400束列不等量关系，难点是列不等关系时是否用取等号．
16．
【分析】（1）根据一次函数的增减性可得y随x增大而减小，把y=0代入即可求出x的值，然后根据一次函数的增减性即可得出结论；
（2）根据题意，画出图象，根据当时，直线在x轴的上方，可得当时，＞0，从而得出结论．
【详解】解：（1）一次函数中，-3＜0
∴y随x增大而减小
当y=0时，解得x=-2
∴y＞0时，x＜-2，
即位于x轴上方的点的横坐标的范围是
故答案为：；
（2）根据题意，画出如下图象
∵直线中，2＞0
∴y随x增大而增大
∵当时，直线在x轴的上方
即当时，＞0
∴的解集为
故答案为：．
【点睛】此题考查的是根据一次函数的增减性求不等式的解集，掌握一次函数增减性与系数的关系和一次函数与一元一次不等式的关系是解决此题的关键．
17．，
【分析】过作轴，交轴于，交于，过作轴，交轴于，，求出，证，推出，，设，求出，得出，求出，得出的坐标，由两点坐标公式求出，在中，由勾股定理求出，得出的坐标，设直线的解析式是，把代入求出直线的解析式，解由两函数解析式组成的方程组，求出方程组的解即可．
【详解】解：过作轴，交轴于，交于，过作轴，交轴于，

，
，，
，
，
，，
在和中，
，
，，
，
设，，
，
，
则，
，即．
直线，
，
点
，
在中，由勾股定理得：，
则的坐标是，
设直线的解析式是，
把代入得：，
即直线的解析式是，
组成方程组
解得：
点，，
故答案为：，．
【点睛】本题是一次函数综合题，考查了用待定系数法求出一次函数的解析式，全等三角形的性质和判定，解方程组，勾股定理，旋转的性质等知识点的应用，主要考查学生综合运用性质进行推理和计算的能力，题目比较好，但是有一定的难度．
18．（，m是弹簧能承受物体的最大质量）
【分析】由题意即可求出挂上xkg的物体后，弹簧伸长的量，再加上弹簧原长即得出y与x的函数关系式，注意自变量的取值范围．
【详解】∵弹簧挂上重物后伸长的长度与所挂重物的质量成正比，且挂上1kg的物体后，弹簧伸长2cm，
∴挂上xkg的物体后，弹簧伸长2xcm．
∵弹簧不挂重物时长12cm，
∴弹簧总长(，m是弹簧能承受物体的最大质量)．
【点睛】本题考查一次函数的实际应用，根据题意找出数量关系列出等式是解答本题的关键．
19．（1）y=2x；y=2.6x-12
（2）55
【详解】试题分析：（1）当0≤x≤20时，y与x的函数表达式是y=2x；…2分
当x＞20时，y与x的函数表达式是y=2×20+2.6（x-20）=2.6x-12；…2分
（2）因为小明家四、五月份的水费都不超过40元，六月份的水费超过40元，
所以把y=30代入y=2x中，得x=15；
把y=34代入y=2x中，得x=17；
把y=47.8代入y=2.6x-12中，得x=23．
所以15+17+23=55．
答：小明家这个季度共用水55立方米．……3分
考点：本题考查了一次函数的应用
点评：此类试题属于难度一般的试题，考生在解答此类试题时一定要注意分析各个变量阶段的要求和函数的求法
20．(1)
(2)存在；或
【分析】本题考查了一次函数的交点问题，用待定系数法求函数解析式，等腰三角形的性质，
（1）先求出 解析式得到，将代入，求解即可；
（2）先求出，得到，，则是等腰直角三角形，得到，再分两种情况讨论即可．
【详解】（1）解：把代入得：
，
解得，
，
当时，，
∴，
将代入，得，
解得，
∴直线的表达式为；
（2）解：当时，，解得，
∴，
∴，，
当时，，即，
∴是等腰直角三角形，
∴；
分以下两种情况：
①过点A作x轴的垂线，交直线于点M，
在 中，令，则，
∴，
即此时是等腰直角三角形，；
②如图，取的中点N，过点N作x轴的垂线，交直线于点，由垂直平分线的性质可得，
∴，
∴，
即此时是等腰直角三角形，
由N为的中点，易得，
在 中，令，则，
∴．
综上，直线上存在点M，使为等腰直角三角形，点M的坐标为或．
21．(1) 8千克(2) y=4x+100，购买甲种原料8千克时，总费用最少
【分析】（1）先由甲种原料所需的质量和饮料的总质量，表示出乙种原料的质量，再结合表格中的数据，根据“至少含有480单位的维生素C”这一不等关系列出不等式，即可求出答案;
（2）根据表中所给的数据列出式子，再根据k的值，即可得出购买甲种原料多少千克时，总费用最少.
【详解】解：（1）依题意，得600x+400（20-x）≥480×20，
解得x≥8.
∴至少需要购买甲种原料8千克.
（2）根据题意得：y=9x+5（20－x），即y=4x+100，
∵k=4＞0，∴y随x的增大而增大.
∵x≥8，∴当x=8时，y最小.
∴购买甲种原料8千克时，总费用最少.
【点睛】本题考查一元一次不等式的应用，一次函数的应用，利用一次函数的增减性判断费用最少是解题的关键.
22．（1），；（2）画图见解析，①，②
【分析】（1）将点分别代入函数和即可求解；
（2）根据描点法画出函数图像，①通过函数图像得到时，自变量的取值范围即可；②观察函数图像，求得且时，自变量的取值范围即可．
【详解】解：（1）将点代入函数得，解得
将点代入函数得，解得
故答案为，
（2）列表，如下
0 2
-2 -1
5 -1
函数图像如下：
①由图像可得：当时，，故答案为
②将代入得，，由图像可知时，
将代入得，，由图像可知时，
由此可得
【点睛】此题考查了待定系数法求解一次函数解析式，一次函数与一元一次不等式的关系，熟练掌握待定系数法以及一次函数与一元一次不等式的关系是解题的关键．
23．；当水价为每吨元时，吨水生产的饮料所获的利润是元
【分析】根据题意，设关于的函数表达式为，将，；，代入解析式即可求解，进而将代入解析式，求得的值，即可求得答案．
【详解】解：根据题意，设关于的函数表达式为，将，；，代入，
得，
解得，
∴，
当时，，
即当水价为每吨元时，吨水生产的饮料所获的利润是元．
【点睛】本题考查了待定系数法求解析式，求函数值，求得解析式是解题的关键．
24．(1)5
(2)
(3)（8，0）、（-2，0）或（-3，0）．
【分析】（1）根据题意求出a、b的值，运用勾股定理可求AB的值；
（2）首先求出点D的坐标，再作点B关于y轴的对称点连接，求解即可；
（3）根据AB是腰分类讨论即可．
【详解】（1）解：∵
∴a=4，b=3
∴OA=4，OB=3
根据勾股定理可得
∴
所以AB长度为5．
（2）解：存在点P，使得PB+PD最小值为
如图；过点D作轴，交y轴于点E，作点B关于y轴的对称点连接，过点D作轴于点F，
∵
∴
在和中
∴
∴OB=AE=3，OA=DE=4
∴点D坐标为（4，7）
∵，DF=7
根据勾股定理可得
∴
∴PB+PD最小值为．
（3）解：当AB=AM时，点M坐标为（-3，0）
当BA=BM时，点M坐标为（8，0）、（-2，0）
∴使以AB为等腰三角形的点M的坐标为（8 ，0）、（-2，0）或（-3，0）．
【点睛】本题是一次函数的综合应用，解题的关键是掌握勾股定理、对称求线段和最小、等腰三角形的判定．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)