第三章投影与视图同步练习(含解析)
图片预览

文档简介
中小学教育资源及组卷应用平台
第三章投影与视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
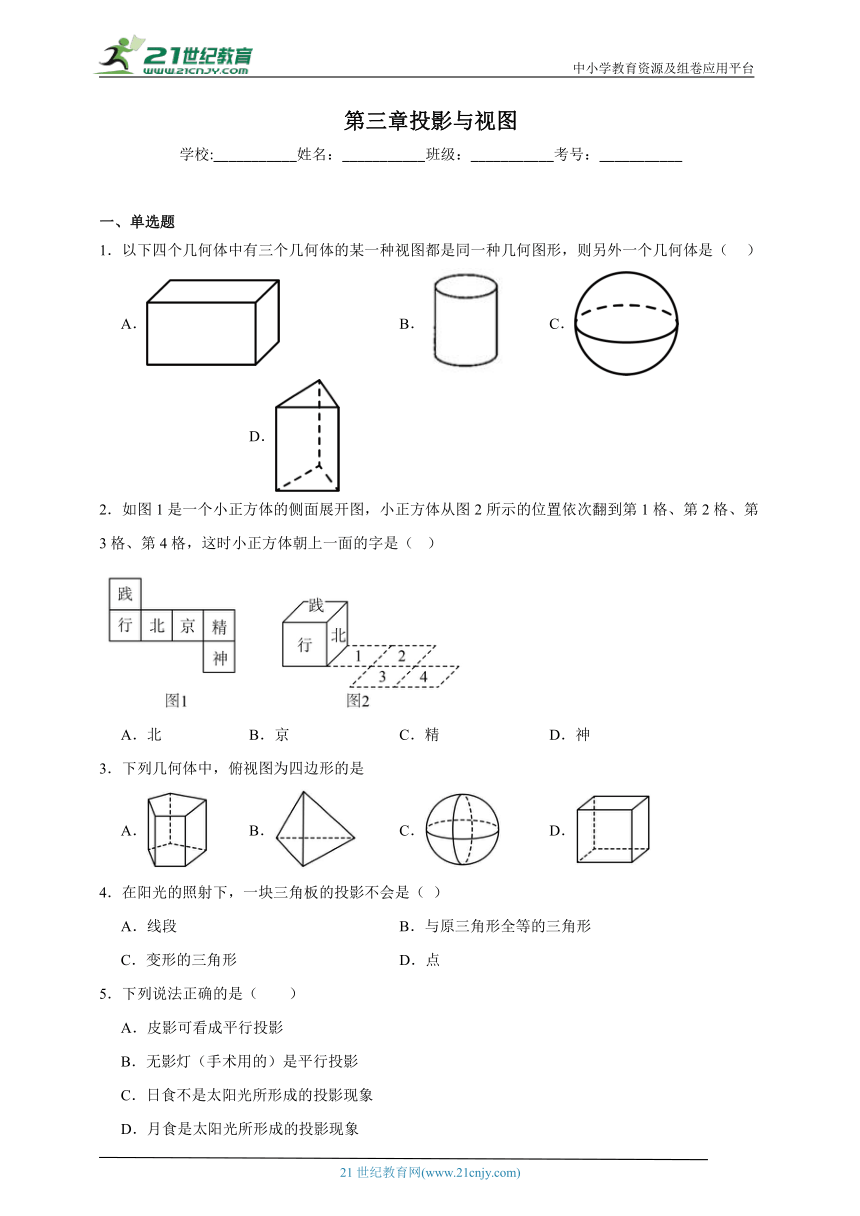
1.以下四个几何体中有三个几何体的某一种视图都是同一种几何图形,则另外一个几何体是( )
A. B. C. D.
2.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
A.北 B.京 C.精 D.神
3.下列几何体中,俯视图为四边形的是
A. B. C. D.
4.在阳光的照射下,一块三角板的投影不会是( )
A.线段 B.与原三角形全等的三角形
C.变形的三角形 D.点
5.下列说法正确的是( )
A.皮影可看成平行投影
B.无影灯(手术用的)是平行投影
C.日食不是太阳光所形成的投影现象
D.月食是太阳光所形成的投影现象
6.某运动会颁奖台如图所示,它的主视图是( )
A. B. C. D.
7.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
8.如图1所示为烽火台,其建筑主体为正四棱台,图2几何体为其结构图.如图2所示,正四棱台是由底面为正方形的正四棱锥切割所得到的,则图2几何体的主视图为( )
A. B. C. D.
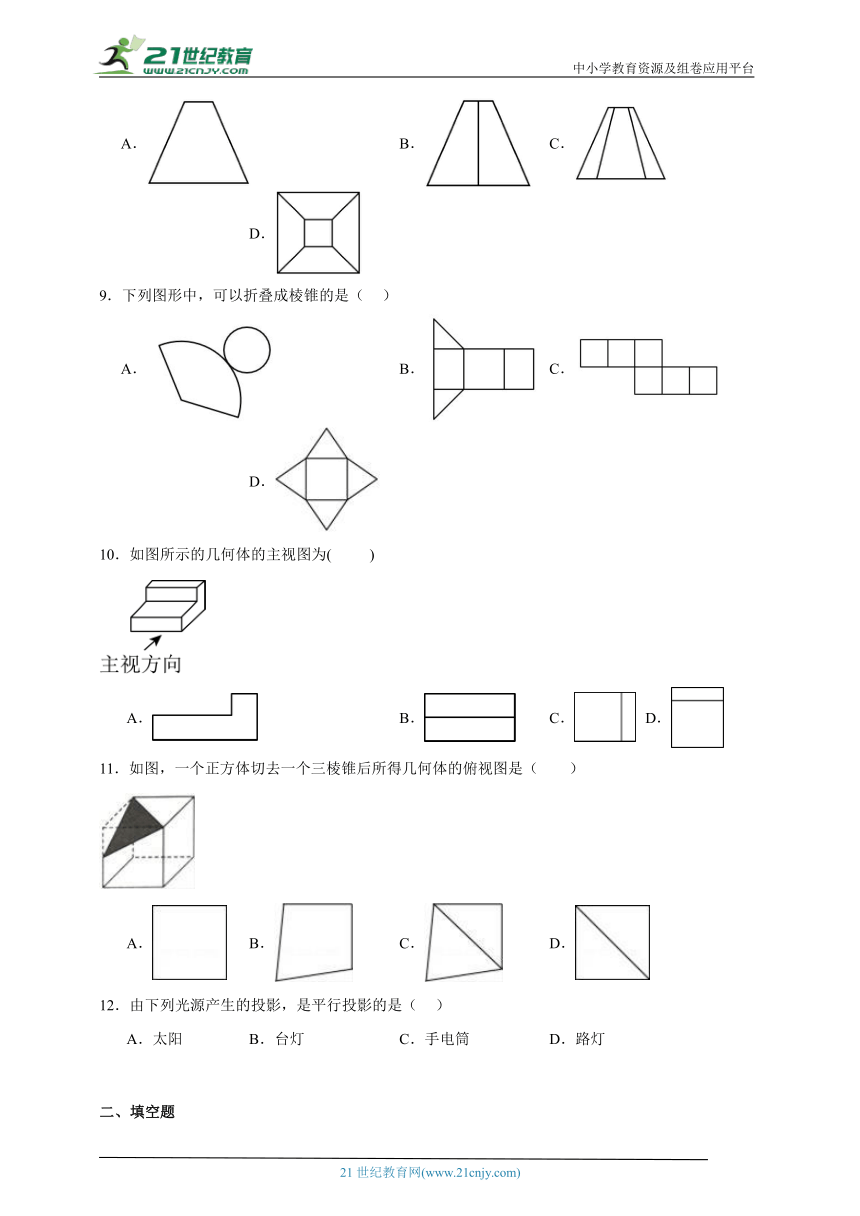
9.下列图形中,可以折叠成棱锥的是( )
A. B. C. D.
10.如图所示的几何体的主视图为( )
A. B. C. D.
11.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
A. B. C. D.
12.由下列光源产生的投影,是平行投影的是( )
A.太阳 B.台灯 C.手电筒 D.路灯
二、填空题
13.常见立体图形长方体、圆柱、圆锥、三棱锥中,侧面展开图是扇形的是 .
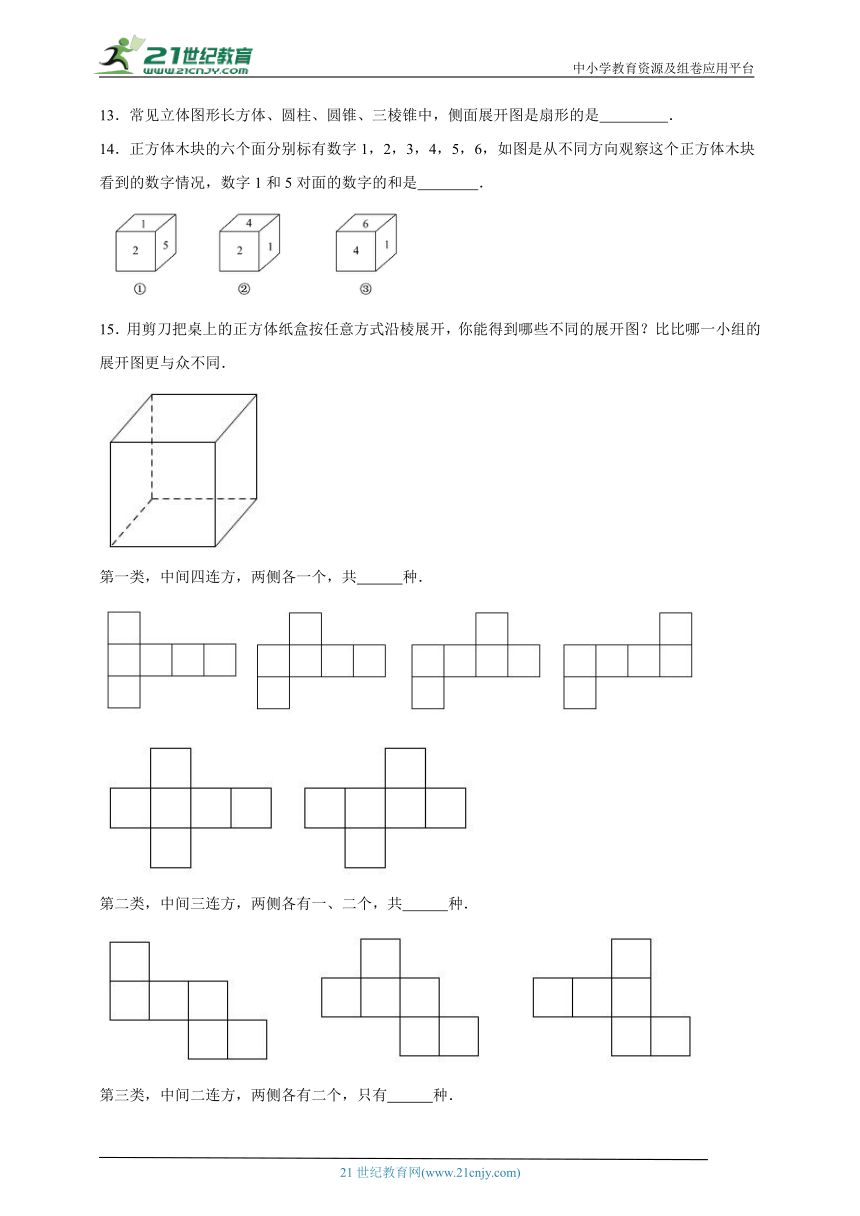
14.正方体木块的六个面分别标有数字1,2,3,4,5,6,如图是从不同方向观察这个正方体木块看到的数字情况,数字1和5对面的数字的和是 .
15.用剪刀把桌上的正方体纸盒按任意方式沿棱展开,你能得到哪些不同的展开图?比比哪一小组的展开图更与众不同.
第一类,中间四连方,两侧各一个,共 种.
第二类,中间三连方,两侧各有一、二个,共 种.
第三类,中间二连方,两侧各有二个,只有 种.
第四类,两排各三个,只有 种.
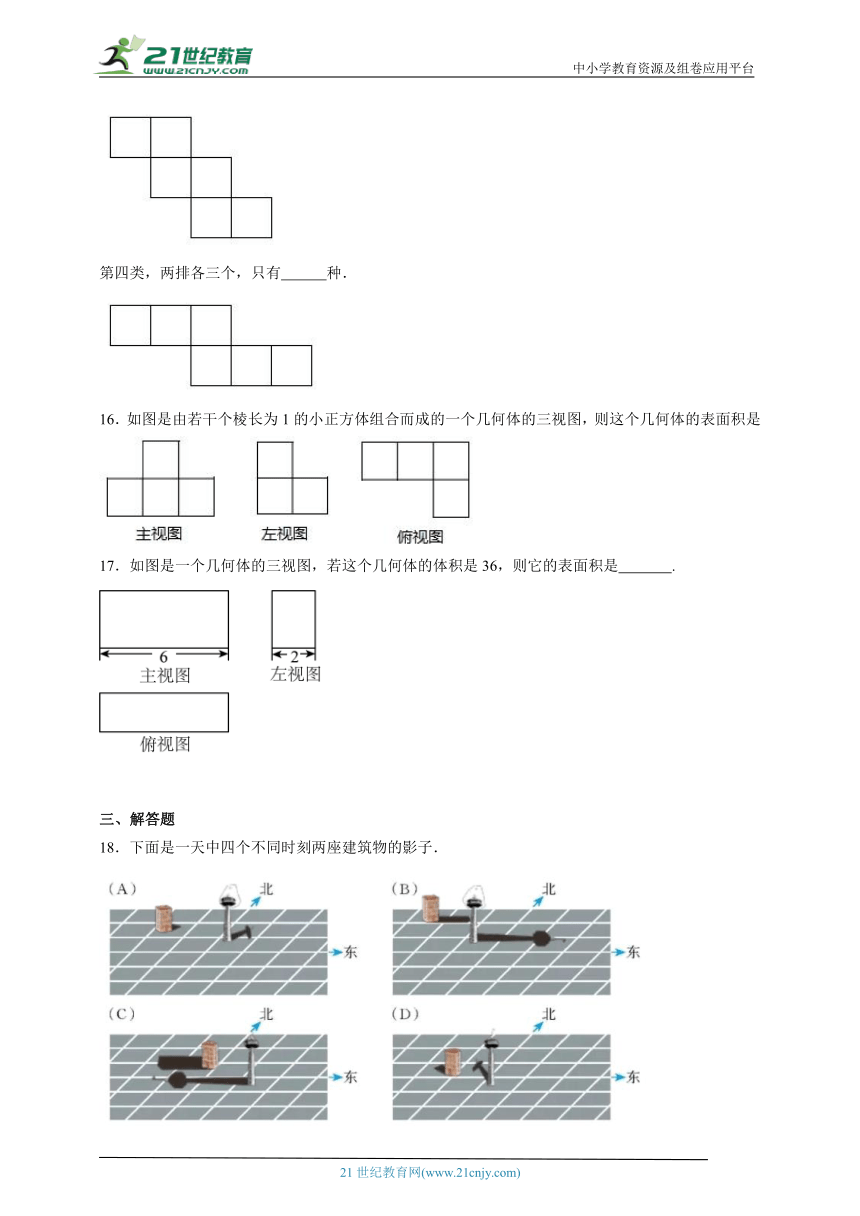
16.如图是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是
17.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 .
三、解答题
18.下面是一天中四个不同时刻两座建筑物的影子.
(1)将它们按时间先后顺序进行排列,并说一说你的理由;
(2)一天当中,物体在太阳光下的影子的方向是如何变化的?
19.如图所示,图1为一个棱长为8的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:
(1)如果正方体相对面上的两个数字之和相等,则______,______.
(2)如果面“10”是左面,面“6”在前面,则上面是______(填“x”或“y”或“2”)
(3)图1中,点M为所在棱的中点,在图2中找点M的位置,直接写出图2中△ABM的面积.
20.画出这个几何体从正面、左面和上面看到的图形.
21.如图是几种几何体的表面展开图,请你分别这几种几何体的名称写出来.
22.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
23.树及其影子、木杆及其影子如图所示,哪个图反了阳光下的情形?哪个图反映了灯光下的情形?说说你的理由.
24.如图,是一个由9个边长为的正方体组成的立体图形.
(1)画出该立体图形的主视图、左视图和俯视图.
(2)若将整个立体图形的表面(包含底部)全部喷上油漆,则被油漆覆盖的面积为______.
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,则最多可以再添加______块小正方体.
《第三章投影与视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D D D C D A D B
题号 11 12
答案 D A
1.C
【分析】长方体、圆柱体和三棱柱的主视图都是矩形,而球的视图都是圆形.
【详解】解:长方体、圆柱、三棱柱为柱体,它们的主视图都是矩形,而球的三种视图都是圆.
故选C.
【点睛】本题考查了简单几何体的三视图的知识,解题关键是要熟练掌握简单几何体的三视图,属于基础题.
2.A
【分析】本题考查正当提相对面上的字;
利用正方体的展开特点得出“践”和“神”相对;“北”和“精”相对;“行”和“京”相对,进一步利用翻转得出答案即可.
【详解】解:由图1可得,“践”和“神”相对;“北”和“精”相对;“行”和“京”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“精”在下面,则这时小正方体朝上面的字是“北”.
故选A.
3.D
【分析】根据俯视图的定义.找到从上面看所得到的图形即可.
【详解】从上面看易得A、B、C、D的俯视图分别为五边形、三角形、圆、四边形.故选D.
【点睛】本题考查简单几何体的三视图.熟练运用三视图的定义判断是解题的关键.
4.D
【分析】将一个三角板放在太阳光下,当它与阳光平行时,它所形成的投影是一条线段;当它与阳光成一定角度但不垂直时,它所形成的投影是三角形.
【详解】解:根据太阳高度角不同,所形成的投影也不同.当三角板与阳光平行时,所形成的投影为一条线段;当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,
故选D.
【点睛】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应视其外在形状,及其与光线的夹角而定.
5.D
【分析】分析各选项可知,皮影和无影灯都是点光源形成的投影,而日食都是太阳光形成的投影;接下来,根据中心投影与平行投影的知识进行分析判断,问题即可得解.
【详解】解:根据平行投影和中心投影的区别可知:皮影和无影灯都是中心投影,而日食是太阳光形成的投影
故选:D.
【点睛】本题主要考查的是中心投影和平行投影的定义,掌握其概念是解决此题的关键.
6.C
【详解】从正面看到的图形如图所示:
,
故选C.
7.D
【分析】因为中心投影物体的高和影长成比例,正确的区分中心投影和平行投影,依次分析选项即可找到符合题意的选项
【详解】因为正方形的对角线互相垂直,且一条对角线垂直地面,光源与对角线组成的平面垂直于地面,则有影子的对角线仍然互相垂直,且由于光源在平板的上方,则上方的边长影子会更长一些,
故选D
【点睛】本题考查了中心投影的概念,应用,利用中心投影的特点,理解中心投影物体的高和影长成比例是解题的关键.
8.A
【分析】本题考查了三视图的知识,找到从正面看所得到的图形即可,注意所有的看到的和看不到的棱都应表现在主视图中.
【详解】解:从几何体的正面可以看到一个等腰梯形.
故选:A.
9.D
【分析】根据展开图的特点即可判断.
【详解】解:A、根据图形判断是圆锥展开图,不符合题意.
B、根据图形判断是三棱柱展开图,不符合题意.
C、根据图形判断是正方体展开图,不符合题意.
D、根据图形判断是四棱锥展开图,符合题意.
故选:D.
【点睛】本题考查几何体展开图的判断,熟悉各个多面体的特征是关键.
10.B
【分析】根据三视图的定义判断即可.
【详解】解:所给几何体是由两个长方体上下放置组合而成,所以其主视图也是上下两个长方形组合而成,且上下两个长方形的宽的长度相同.
故选B.
【点睛】本题考查了三视图知识.
11.D
【分析】俯视图是从上向下看得到的视图,结合选项即可作出判断.
【详解】所给图形的俯视图如图所示:
,
故选D.
【点睛】本题考查了俯视图,明确俯视图是从物体上面看得到的图形是解题的关键.
12.A
【分析】根据平行投影和中心投影的定义进行判断.
【详解】解:用光线照射物体所产生的投影为平行投影,而用路灯、手电筒、台灯等照射物体所产生的投影为中心投影,
故选A.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
13.圆锥
【分析】圆锥的侧面展开图是扇形.
【详解】解:根据圆锥的特征可知,侧面展开图是扇形的是圆锥.
故答案为:圆锥
【点睛】本题主要考查简单几何体的侧面展开图,解题时勿忘记圆锥的特征及圆锥展开图的情形.
14.7
【分析】根据所给正方体以及从不同方向观察物体的特点可知,1对面的数字是3,5对面的数字是4,所以数字1和5对面的数字的和是3+4.
【详解】解:由图①知,1对面的数字可能是3,4,6,
再由图②③知,4和1相邻,6和1也相邻,则1对面的数字只可能是3,
同理,5对面的数字是4,
则3+4=7,
答:数字1和5对面的数字的和是7.
故答案为:7.
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力.
15. 六 三 一 一
【解析】略
16.22
【分析】利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
【详解】解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6-8=22,
故答案为:22.
【点睛】本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”是解题的关键.
17.72
【详解】分析:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,
∴设高为h,则6×2×h=36,解得:h=3.
∴它的表面积是:2×3×2+2×6×2+3×6×2=72.
18.(1)(C)(D)(A)(B),理由见解析;(2)正西、北偏西、正北、北偏东、正东.
【分析】太阳的位置和高度决定了影子的方向和长短.一天中,阳光下物体的影子变化规律是上午影子由长逐渐变短,下午影子由短逐渐变长,方向由西逐渐转向东.
【详解】(1)通过观察分析图片可知,按照时间先后排序为(C)(D)(A)(B).判断依据是影子与太阳的位置相反,上午影子在西方,随着太阳的运动,影子逐渐转向东方.
(2)通过观察可知,一天中,阳光下物体的影子变化规律是方向随着太阳位置的变化而变化,由西逐渐转向东,所以物体在阳光下的影子的方向是:正西、北偏西、正北、北偏东、正东.
【点睛】掌握一天中物体影子的变化规律,是解答本题的关键。
19.(1)12;8(2)2;(3)16或80
【分析】(1)正方体展开图中,相对的两个面之间必然隔着一个正方形,由此知道“2”与“x”是相对面,“4”与“10”是相对面,“6”与“y”是相对面,由相对面两个数之和相等,列式计算即可;
(2)由相邻面和相对面的关系,分析判断即可得到答案;
(3)由点M所在的棱为两个面共用,可以判断得到点M的位置,根据三角形面积公式,即可得到答案.
【详解】解:(1)∵正方体相对面上的两个数字之和相等
∴,
∴,
故答案为:12;8
(2)若面“10”是左面,面“6”在前面,则上面是“2”
(3)因为点M所在的棱为两个面共用,所以它的位置有两种情况,第一种情况如下图:
设点M左边的顶点为点D,则
第二种情况如下图:
综上所述,的面积为:16或80
【点睛】本题考查正方体的展开图,能够准确区分展开图的相对面和相邻面是解题的关键.
20.见解析
【分析】根据三视图的定义结合图形画图即可.
【详解】
解:如图所示,
【点睛】本题考查作图-三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
21.圆锥;圆柱;四棱锥
【解析】略
22.(1)树AB的高约为4m;(2)8m.
【分析】(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,再根据当树与地面成60°角时影长最大,根据三角函数即可求解.
【详解】解:(1)AB=ACtan30°=12× = (米).
答:树高约为 米.
(2)如图(2),B1N=AN=AB1sin45°=× =(米).
NC1=NB1tan60°= × = (米).
AC1=AN+NC1= + .
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2= ;
23.图(1)反映了灯光下的情形,图(2)反映了阳光下的情形,理由见解析.
【分析】根据中心投影与平行投影的特点即可判断.
【详解】如图所示,图(1)反映了灯光下的情形,图(2)反映了阳光下的情形.
【点睛】本题主要考查中心投影与平行投影的区别.中心投影的投射线相交于投影中心,而平行投影的投射线是相互平行的.
24.(1)见解析
(2)
(3)6
【分析】本题考查了几何体的主视图、左视图和俯视图.
(1)根据主视图、左视图和俯视图的定义画图即可;
(2)根据表面积的计算方法求解即可;
(3)根据三视图的特点解答即可.
【详解】(1)如图,
(2).
故答案为:;
(3)如图,保持主视图和左视图不变,则最多可以再添加6块小正方体.
故答案为:6;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第三章投影与视图
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.以下四个几何体中有三个几何体的某一种视图都是同一种几何图形,则另外一个几何体是( )
A. B. C. D.
2.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格、第4格,这时小正方体朝上一面的字是( )
A.北 B.京 C.精 D.神
3.下列几何体中,俯视图为四边形的是
A. B. C. D.
4.在阳光的照射下,一块三角板的投影不会是( )
A.线段 B.与原三角形全等的三角形
C.变形的三角形 D.点
5.下列说法正确的是( )
A.皮影可看成平行投影
B.无影灯(手术用的)是平行投影
C.日食不是太阳光所形成的投影现象
D.月食是太阳光所形成的投影现象
6.某运动会颁奖台如图所示,它的主视图是( )
A. B. C. D.
7.如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
8.如图1所示为烽火台,其建筑主体为正四棱台,图2几何体为其结构图.如图2所示,正四棱台是由底面为正方形的正四棱锥切割所得到的,则图2几何体的主视图为( )
A. B. C. D.
9.下列图形中,可以折叠成棱锥的是( )
A. B. C. D.
10.如图所示的几何体的主视图为( )
A. B. C. D.
11.如图,一个正方体切去一个三棱锥后所得几何体的俯视图是( )
A. B. C. D.
12.由下列光源产生的投影,是平行投影的是( )
A.太阳 B.台灯 C.手电筒 D.路灯
二、填空题
13.常见立体图形长方体、圆柱、圆锥、三棱锥中,侧面展开图是扇形的是 .
14.正方体木块的六个面分别标有数字1,2,3,4,5,6,如图是从不同方向观察这个正方体木块看到的数字情况,数字1和5对面的数字的和是 .
15.用剪刀把桌上的正方体纸盒按任意方式沿棱展开,你能得到哪些不同的展开图?比比哪一小组的展开图更与众不同.
第一类,中间四连方,两侧各一个,共 种.
第二类,中间三连方,两侧各有一、二个,共 种.
第三类,中间二连方,两侧各有二个,只有 种.
第四类,两排各三个,只有 种.
16.如图是由若干个棱长为1的小正方体组合而成的一个几何体的三视图,则这个几何体的表面积是
17.如图是一个几何体的三视图,若这个几何体的体积是36,则它的表面积是 .
三、解答题
18.下面是一天中四个不同时刻两座建筑物的影子.
(1)将它们按时间先后顺序进行排列,并说一说你的理由;
(2)一天当中,物体在太阳光下的影子的方向是如何变化的?
19.如图所示,图1为一个棱长为8的正方体,图2为图1的表面展开图(数字和字母写在外表面上,字母也可以表示数),请根据要求回答问题:
(1)如果正方体相对面上的两个数字之和相等,则______,______.
(2)如果面“10”是左面,面“6”在前面,则上面是______(填“x”或“y”或“2”)
(3)图1中,点M为所在棱的中点,在图2中找点M的位置,直接写出图2中△ABM的面积.
20.画出这个几何体从正面、左面和上面看到的图形.
21.如图是几种几何体的表面展开图,请你分别这几种几何体的名称写出来.
22.某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
23.树及其影子、木杆及其影子如图所示,哪个图反了阳光下的情形?哪个图反映了灯光下的情形?说说你的理由.
24.如图,是一个由9个边长为的正方体组成的立体图形.
(1)画出该立体图形的主视图、左视图和俯视图.
(2)若将整个立体图形的表面(包含底部)全部喷上油漆,则被油漆覆盖的面积为______.
(3)如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,则最多可以再添加______块小正方体.
《第三章投影与视图》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D D D C D A D B
题号 11 12
答案 D A
1.C
【分析】长方体、圆柱体和三棱柱的主视图都是矩形,而球的视图都是圆形.
【详解】解:长方体、圆柱、三棱柱为柱体,它们的主视图都是矩形,而球的三种视图都是圆.
故选C.
【点睛】本题考查了简单几何体的三视图的知识,解题关键是要熟练掌握简单几何体的三视图,属于基础题.
2.A
【分析】本题考查正当提相对面上的字;
利用正方体的展开特点得出“践”和“神”相对;“北”和“精”相对;“行”和“京”相对,进一步利用翻转得出答案即可.
【详解】解:由图1可得,“践”和“神”相对;“北”和“精”相对;“行”和“京”相对;
由图2可得,小正方体从图2的位置依次翻到第4格时,“精”在下面,则这时小正方体朝上面的字是“北”.
故选A.
3.D
【分析】根据俯视图的定义.找到从上面看所得到的图形即可.
【详解】从上面看易得A、B、C、D的俯视图分别为五边形、三角形、圆、四边形.故选D.
【点睛】本题考查简单几何体的三视图.熟练运用三视图的定义判断是解题的关键.
4.D
【分析】将一个三角板放在太阳光下,当它与阳光平行时,它所形成的投影是一条线段;当它与阳光成一定角度但不垂直时,它所形成的投影是三角形.
【详解】解:根据太阳高度角不同,所形成的投影也不同.当三角板与阳光平行时,所形成的投影为一条线段;当它与阳光形成一定角度但不垂直时,它所形成的投影是三角形,不可能是一个点,
故选D.
【点睛】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同,具体形状应视其外在形状,及其与光线的夹角而定.
5.D
【分析】分析各选项可知,皮影和无影灯都是点光源形成的投影,而日食都是太阳光形成的投影;接下来,根据中心投影与平行投影的知识进行分析判断,问题即可得解.
【详解】解:根据平行投影和中心投影的区别可知:皮影和无影灯都是中心投影,而日食是太阳光形成的投影
故选:D.
【点睛】本题主要考查的是中心投影和平行投影的定义,掌握其概念是解决此题的关键.
6.C
【详解】从正面看到的图形如图所示:
,
故选C.
7.D
【分析】因为中心投影物体的高和影长成比例,正确的区分中心投影和平行投影,依次分析选项即可找到符合题意的选项
【详解】因为正方形的对角线互相垂直,且一条对角线垂直地面,光源与对角线组成的平面垂直于地面,则有影子的对角线仍然互相垂直,且由于光源在平板的上方,则上方的边长影子会更长一些,
故选D
【点睛】本题考查了中心投影的概念,应用,利用中心投影的特点,理解中心投影物体的高和影长成比例是解题的关键.
8.A
【分析】本题考查了三视图的知识,找到从正面看所得到的图形即可,注意所有的看到的和看不到的棱都应表现在主视图中.
【详解】解:从几何体的正面可以看到一个等腰梯形.
故选:A.
9.D
【分析】根据展开图的特点即可判断.
【详解】解:A、根据图形判断是圆锥展开图,不符合题意.
B、根据图形判断是三棱柱展开图,不符合题意.
C、根据图形判断是正方体展开图,不符合题意.
D、根据图形判断是四棱锥展开图,符合题意.
故选:D.
【点睛】本题考查几何体展开图的判断,熟悉各个多面体的特征是关键.
10.B
【分析】根据三视图的定义判断即可.
【详解】解:所给几何体是由两个长方体上下放置组合而成,所以其主视图也是上下两个长方形组合而成,且上下两个长方形的宽的长度相同.
故选B.
【点睛】本题考查了三视图知识.
11.D
【分析】俯视图是从上向下看得到的视图,结合选项即可作出判断.
【详解】所给图形的俯视图如图所示:
,
故选D.
【点睛】本题考查了俯视图,明确俯视图是从物体上面看得到的图形是解题的关键.
12.A
【分析】根据平行投影和中心投影的定义进行判断.
【详解】解:用光线照射物体所产生的投影为平行投影,而用路灯、手电筒、台灯等照射物体所产生的投影为中心投影,
故选A.
【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.
13.圆锥
【分析】圆锥的侧面展开图是扇形.
【详解】解:根据圆锥的特征可知,侧面展开图是扇形的是圆锥.
故答案为:圆锥
【点睛】本题主要考查简单几何体的侧面展开图,解题时勿忘记圆锥的特征及圆锥展开图的情形.
14.7
【分析】根据所给正方体以及从不同方向观察物体的特点可知,1对面的数字是3,5对面的数字是4,所以数字1和5对面的数字的和是3+4.
【详解】解:由图①知,1对面的数字可能是3,4,6,
再由图②③知,4和1相邻,6和1也相邻,则1对面的数字只可能是3,
同理,5对面的数字是4,
则3+4=7,
答:数字1和5对面的数字的和是7.
故答案为:7.
【点睛】本题是考查从不同方向观察物体和几何图形,是培养学生的观察能力.
15. 六 三 一 一
【解析】略
16.22
【分析】利用主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,进而判断图形形状,即可得出小正方体的个数.
【详解】解:综合三视图,我们可以得出,这个几何模型的底层有3+1=4个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是4+1=5个.
∴这个几何体的表面积是5×6-8=22,
故答案为:22.
【点睛】本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”是解题的关键.
17.72
【详解】分析:∵由主视图得出长方体的长是6,宽是2,这个几何体的体积是36,
∴设高为h,则6×2×h=36,解得:h=3.
∴它的表面积是:2×3×2+2×6×2+3×6×2=72.
18.(1)(C)(D)(A)(B),理由见解析;(2)正西、北偏西、正北、北偏东、正东.
【分析】太阳的位置和高度决定了影子的方向和长短.一天中,阳光下物体的影子变化规律是上午影子由长逐渐变短,下午影子由短逐渐变长,方向由西逐渐转向东.
【详解】(1)通过观察分析图片可知,按照时间先后排序为(C)(D)(A)(B).判断依据是影子与太阳的位置相反,上午影子在西方,随着太阳的运动,影子逐渐转向东方.
(2)通过观察可知,一天中,阳光下物体的影子变化规律是方向随着太阳位置的变化而变化,由西逐渐转向东,所以物体在阳光下的影子的方向是:正西、北偏西、正北、北偏东、正东.
【点睛】掌握一天中物体影子的变化规律,是解答本题的关键。
19.(1)12;8(2)2;(3)16或80
【分析】(1)正方体展开图中,相对的两个面之间必然隔着一个正方形,由此知道“2”与“x”是相对面,“4”与“10”是相对面,“6”与“y”是相对面,由相对面两个数之和相等,列式计算即可;
(2)由相邻面和相对面的关系,分析判断即可得到答案;
(3)由点M所在的棱为两个面共用,可以判断得到点M的位置,根据三角形面积公式,即可得到答案.
【详解】解:(1)∵正方体相对面上的两个数字之和相等
∴,
∴,
故答案为:12;8
(2)若面“10”是左面,面“6”在前面,则上面是“2”
(3)因为点M所在的棱为两个面共用,所以它的位置有两种情况,第一种情况如下图:
设点M左边的顶点为点D,则
第二种情况如下图:
综上所述,的面积为:16或80
【点睛】本题考查正方体的展开图,能够准确区分展开图的相对面和相邻面是解题的关键.
20.见解析
【分析】根据三视图的定义结合图形画图即可.
【详解】
解:如图所示,
【点睛】本题考查作图-三视图.在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.本题画几何体的三视图时应注意小正方形的数目及位置.
21.圆锥;圆柱;四棱锥
【解析】略
22.(1)树AB的高约为4m;(2)8m.
【分析】(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,再根据当树与地面成60°角时影长最大,根据三角函数即可求解.
【详解】解:(1)AB=ACtan30°=12× = (米).
答:树高约为 米.
(2)如图(2),B1N=AN=AB1sin45°=× =(米).
NC1=NB1tan60°= × = (米).
AC1=AN+NC1= + .
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2= ;
23.图(1)反映了灯光下的情形,图(2)反映了阳光下的情形,理由见解析.
【分析】根据中心投影与平行投影的特点即可判断.
【详解】如图所示,图(1)反映了灯光下的情形,图(2)反映了阳光下的情形.
【点睛】本题主要考查中心投影与平行投影的区别.中心投影的投射线相交于投影中心,而平行投影的投射线是相互平行的.
24.(1)见解析
(2)
(3)6
【分析】本题考查了几何体的主视图、左视图和俯视图.
(1)根据主视图、左视图和俯视图的定义画图即可;
(2)根据表面积的计算方法求解即可;
(3)根据三视图的特点解答即可.
【详解】(1)如图,
(2).
故答案为:;
(3)如图,保持主视图和左视图不变,则最多可以再添加6块小正方体.
故答案为:6;
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
