第四章概率同步练习(含解析)
图片预览




文档简介
中小学教育资源及组卷应用平台
第四章概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( )
A.0 B. C. D.1
2.某班体育委员的抽屉里有5个乒乓球,其中有三个是白色的,两个是黄色的,上体育课的时候,他随手从抽屉里同时拿了两个乒乓球,则他所拿的乒乓球恰好一个白色一个黄色的概率为( ).
A. B. C. D.
3.下列四个命题中,真命题是( )
A.“任意四边形内角和为360°”是不可能事件
B.“湘潭市明天会下雨”是必然事件
C.“预计本题的正确率是95%”表示100位考生中一定有95人做对
D.抛掷一枚质地均匀的硬币,正面朝上的概率是
4.学校给同学们准备了亚运吉祥物“琼琼、宸宸、莲莲”.设同学选择任意一种吉祥物的机会均等.小聪和小慧可以从三种吉祥物中任选一件,则小聪和小慧拿到同一种吉祥物的概率是( )
A. B. C. D.
5.一个不透明袋子中有3个黑球,5个白球,这些球除颜色外无其它差别.从袋子中随机取出1个球,下列说法正确的是( )
A.能够事先确定取出球的颜色 B.取到黑球的可能性更大
C.取到黑球和取到白球的可能性一样大 D.取到白球的可能性更大
6.“明天下雨的概率是”,下列说法正确的是( )
A.明天一定下雨 B.明天一定不下雨
C.明天的地方下雨 D.明天下雨的可能性比较大
7.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为( )
A.20 B.30 C.40 D.50
8.一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同,红球、黄球、黑球的个数之比为5:3:1,则从布袋里任意摸出一个球是黄球的概率是( )
A. B. C. D.
9.下列事件是随机事件的是( )
A.通常情况温度降到0℃以下,纯净的水结冰;
B.随意翻到一本书的某页,这页的页码是偶数;
C.度量三角形的内角和,结果是360°;
D.测量某天的最低气温,结果为-180℃.
10.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
11.在一次抽奖中,若抽中的概率是0.34,则抽不中的概率是( )
A.0.34 B.0.17 C.0.66 D.0.76
12.如图,是一个可以自由转动的转盘,它被分成三个面积相等的扇形,任意转动转盘两次,当转盘停止后,指针所指颜色相同的概率为( )
A. B. C. D.
二、填空题
13.同时投掷两个骰子,它们点数之和不大于4的概率是 .
14.质地均匀的正四面体骰子的四个面上分别写有数字:2,3,4,5.投掷这个正四面体两次,则第一次底面上的数字能够整除第二次底面上的数字的概率是
15.做重复实验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率为 .
16.在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到一个 可以估计这个事件发生的概率.
17.从一副扑克牌(除去大、小王)中任抽一张,则抽到红心的概率为 ;抽到黑桃的概率为 ;抽到红心3的概率为 .
三、解答题
18.小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
19.甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
20.家乐福超市“端午节”举行有奖促销活动:凡一次性购物满200元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖金依次为48元、40元、32元.一次性购物满200元者,如果不摇奖可返还现金15元.
(1)摇奖一次,获一等奖的概率是多少?
(2)小明一次性购物满了200元,他是参与摇奖划算还是领15元现金划算,请你帮他算算.
21.对某篮球运动员进行3分球投篮测试结果如表所示:
投篮次数 10 50 100 150 200
命中次数 4 25 65 90 120
命中率
(1)计算表中投篮50次、100次、150次、200次相应的命中率;
(2)这个运动员3分球投篮命中的概率约是多少?
(3)估计这个运动员3分球投篮30次能得多少分.
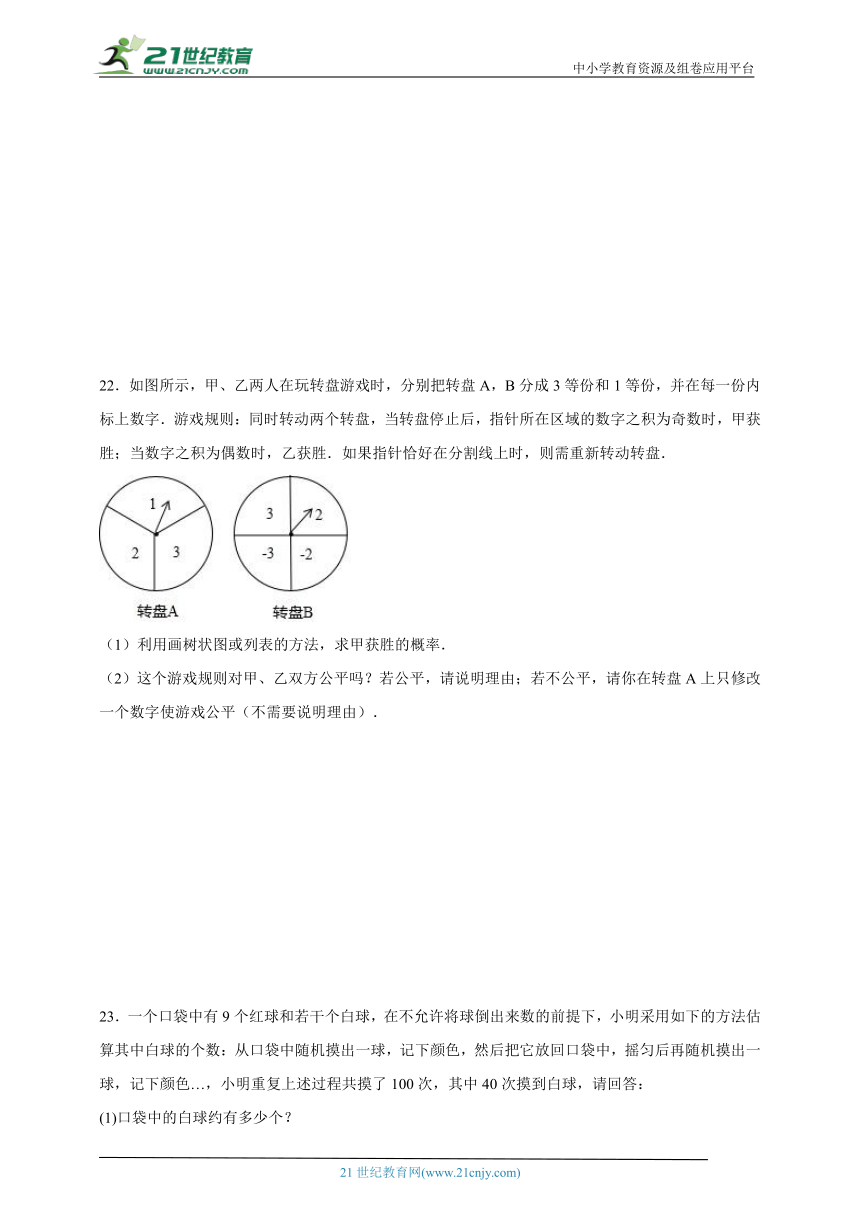
22.如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
23.一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球?
24.在一个口袋里有大小形状都一样的10张卡片,分别写有-1,-2,-3,-4,-5,1,2,3,4,5.从中任意抽出一张卡片.
(1)抽到正数的可能性大还是抽到负数的可能性大?
(2)抽到奇数的可能性大还是抽到偶数的可能性大?
(3)抽到小于2的可能性大还是抽到大于-3的可能性大?
(4)抽到平方数的可能性大还是抽到立方数的可能性大?
(5)抽到绝对值大于1的可能性大还是抽到绝对值小于6的可能性大?
《第四章概率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C D D A B B C
题号 11 12
答案 C A
1.D
【分析】根据题意找出组成命题的所有等可能的情况数,找出组成的命题是真命题的情况数,即可求出所求的概率.
【详解】所有等可能的情况有3种,分别为①② ③;①③ ②;②③ ①,其中组成命题是真命题的情况有:①② ③;①③ ②;②③ ①,则P=1.
故选D.
【点睛】本题考查了用列举法求概率,平行线的性质与判定,等腰三角形的判定与性质,以及命题与定理,弄清题意是解答本题的关键.
2.A
【分析】本题考查的是利用画树状图或列表法求解随机事件的概率,先列表得到所有等可能的结果数有20种,所拿的乒乓球恰好一个白色一个黄色的情况有:种,再利用概率公式计算即可.
【详解】解:用,,表示三个白色乒乓球, ,表示两个黄色的乒乓球,
列表如下:
所有等可能的结果数有20种,他所拿的乒乓球恰好一个白色一个黄色的情况有:种,
∴恰好一个白色一个黄色的概率为.
故选A
3.D
【详解】试题分析:A.“任意四边形内角和为360°”是必然事件,错误;
B.“湘潭市明天会下雨”是随机事件,错误;
C.“预计本题的正确率是95%”表示100位考生中不一定有95人做对,错误;
D.抛掷一枚质地均匀的硬币,正面朝上的概率是,正确.
故选D.
考点:命题与定理.
4.C
【分析】画树状图展示所有9种等可能的情况数.找出符合条件的情况数,然后根据概率公式求解即可.
【详解】解:画树状图为:
共有9种等可能的情况数.其中小聪和小慧拿到同一种吉祥物的有3种情况,
则小聪和小慧拿到同一种吉祥物的概率是.
故选:C.
【点睛】本题考查的列表法与树状补法利用列表或树状图法展示所有或树状图法展示所有可能的结果,求出n.再从中选出符合事件a或b的结果数目m.然后根据概率公式计算事件a或事件b的概率
5.D
【分析】根据不同颜色的球的数量确定摸到哪种球的可能性的大小后即可确定正确的选项
【详解】解:不透明袋子中有3个黑球、5个白球,这些球除颜色外其它无差别,
白球数量大于黑球数量,其摸球具有随机性,
摸到白球的可能性大于摸到黑球的可能性,
故选D
【点睛】本题考查了可能性的大小的知识,哪种球的数量大,摸到这种球的可能性就大
6.D
【分析】本题考查了概率的意义,解决本题的关键是理解概率表示随机事件发生的可能性大小;
根据概率的意义找到正确选项即可.
【详解】解:明天下雨的概率是,说明明天下雨的可能性比较大.所以只有D合题意.
故选:D.
7.A
【详解】分析:根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据白球个数确定出总个数,进而确定出黑球个数n.
详解:根据题意得: ,
计算得出:n=20,
故选A.
点睛:根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
8.B
【详解】分析:用黄球所占的份数除以所有份数的和即可求得是黄球的概率.
详解:∵红球、黄球、黑球的个数之比为5:3:1,
∴从布袋里任意摸出一个球是黄球的概率是.
故选B.
点睛:此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.
9.B
【详解】试题分析:一个概率事件分为:确定事件(包括:必然事件与不可能事件)和随机事件.必然事件发生的可能性是“1”,不可能事件发生的可能性是“0”,随机事件发生的可能性为“0~1”之间.据此可以判断答案B是正确的.
试题解析:A.通常情况温度降到0℃以下,纯净的水结冰,这是一个必然事件,发生的可能性是“1”;
B.随意翻到一本书的某页,这页的页码是偶数,这是一个不确定事件,发生的可能性是“0.5”;这页的页码也可能是奇数;
C.度量三角形的内角和,结果是360°,这是一个不可能事件,发生的可能性是“0”;三角形内角和为180°;
D.测量某天的最低气温,结果为-180°,这是一个不可能事件,发生的可能性是“0”.
故选B.
考点:随机事件.
10.C
【分析】利用列表法或树状图即可解决.
【详解】分别用r、b代表红色帽子、黑色帽子,用R、B、W分别代表红色围巾、黑色围巾、白色围巾,列表如下:
R B W
r rR rB rW
b bR bB bW
则所有可能的结果数为6种,其中恰好为红色帽子和红色围巾的结果数为1种,根据概率公式,恰好为红色帽子和红色围巾的概率是.
故选:C.
【点睛】本题考查了简单事件的概率,常用列表法或画树状图来求解.
11.C
【详解】在一次抽奖中,抽中的概率和抽不中的概率之和是1,抽中的概率是0.34,则抽不中的概率是1-0.34=0.66,故选C.
12.A
【详解】列表得:
红 黄 蓝
红 (红,红) (黄,红) (蓝,红)
黄 (红,黄) (黄,黄) (蓝,黄)
蓝 (红,蓝) (黄,蓝) (蓝,蓝)
由表格可知,所有等可能的情况数有9种,其中颜色相同的情况有3种,则任意转动转盘两次,当转盘停止后,指针所指颜色相同的概率为 .故选A.
13.
【详解】试题分析:根据题意,设第一颗骰子的点数为x,第二颗骰子的点数为y,用(x,y)表示抛掷两个骰子的点数情况,由分步计数原理可得(x,y)的情况数目,由列举法可得其中x+y≤4的情况数目,进而由等可能事件的概率公式计算可得答案.
考点:列表法与树状图法
14.
【详解】试题解析:由树状图
可知共有4×4=16种可能,第一次底面上的数字能够整除第二次底面上的数字的有5种,所以概率是.
故答案为.
15.0.56.
【分析】由于事件“凸面向上”和“凹面向上”是对立事件,根据对立事件的概率和为1计算即可.
【详解】瓶盖只有两面,“凸面向上”的频率约为0.44,
则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为1﹣0.44=0.56,
故答案为0.56.
【点睛】本题主要考查概率的意义、等可能事件的概率,解答此题关键是要明白瓶盖只有两面,即凸面和凹面.
16.常数
【详解】随着实验次数的增加,隐含的规律逐渐显现,事件发生的频率逐渐稳定到某一个数值,所以,我们可以用平稳时的频率去估计这一随机事件在每次实验时发生的机会的大小,在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到一个常数可以估计这个事件发生的概率,故答案为:常数.
17.
【分析】根据题意可得:这幅牌中共有52张,其中到红心13张,黑桃13张,红心3只有1张,故从中任抽一张,抽到红心的概率为,抽到黑桃的概率为;抽到红心3的概率为.
【详解】抽到红心的概率为,抽到黑桃的概率为;抽到红心3的概率为.
故答案为:;;.
【点睛】本题考查了概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A).
18.见解析
【详解】解:根据题意,列表得:
,,
所以小刚得1分的概率为,小明得1分的概率为,
因为,所以游戏对双方不公平.
修改方法不唯一,
若其中一个转盘转出红色,另一个转盘转出了蓝色,则可以配成紫色,此时小刚得7分,否则小明得2分.
也可以修改规则,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色,此时小刚得1分;若两个转盘转出的颜色相同,则小明得1分;否则两人均不得分.
故答案为:不公平,修改方式见上面解析.
红 白 蓝
红 (红,红) (红,白) (红,蓝)
黄 (黄,红) (黄,白) (黄,蓝)
蓝 (蓝,红) (蓝,白) (蓝,蓝)
19.不公平,理由见解析.
【分析】游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】解:这个游戏不公平,游戏所有可能出现的结果如下表:
第二次 第一次 3 4 5 6
3 33 34 35 36
4 43 44 45 46
5 53 54 55 56
6 63 64 65 66
表中共有16种等可能结果,小于45的两位数共有6种.
∴
∵
∴这个游戏不公平.
【点睛】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
20.(1) ;(2) 转转盘划算.
【分析】(1)找到红色区域的份数占总份数的多少即为获得一等奖的概率,
(2)游戏是否合算,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】解:(1)整个圆周被分成了16份,红色为1份,
∴获得一等奖的概率为:,
(2)转转盘:元,
∵16元>15元,
∴转转盘划算.
【点睛】本题主要考查了古典型概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,难度适中.
21.(1);;;
(2)
(3)54分
【分析】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用频率估计概率得到的是近似值,随实验次数的增多,得到的值越来越精确,还考查了频率的计算公式.
(1)用对应的m除以n即可求解;
(2)根据(1)的计算结论可估计这个运动员投篮3分球命中率约为;
(3)根据(2) 的估计得到投篮30次命中次,然后用18乘以3即可.
【详解】(1)解:投篮50次、100次、150次、200次相应的命中率分别为:
;;;;
(2)解:由表格数据知,当投篮次数逐渐增加时,命中率稳定在附近,所以估计这个运动员3分球投篮.
(3)解:由(2)的结论可知这个运动员投篮30次,命中的次数约为(次),约能得到(分).
22.(1)见解析,甲获胜概率为;(2)这个游戏规则对甲、乙双方不公平,将转盘A上的数字2改为1,则游戏公平.
【分析】(1)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得;
(2)先计算出数字之积为偶数的概率,判断概率是否相等即可得知游戏是否公平.
【详解】解:(1)列表如下:
﹣2 ﹣3 2 3
1 ﹣2 ﹣3 2 3
2 ﹣4 ﹣6 4 6
3 ﹣6 ﹣9 6 9
由表可知,共有12种等可能结果,其中指针所在区域的数字之积为奇数的有4种结果,
所以甲获胜概率为;
(2)∵指针所在区域的数字之积为偶数的概率为,
∴这个游戏规则对甲、乙双方不公平,
将转盘A上的数字2改为1,则游戏公平.
【点睛】此题考查了游戏的公平性,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平,用到的知识点为:概率=所求情况数与总情况数之比.
23.(1)小明可估计口袋中的白球的个数是6个.
(2)需准备720个红球.
【详解】试题分析:
(1)用白球的个数:(白球的个数+红球的个数)=40:100,列方程求解;
(2)用彩球的总数乘以,即可得到红球的个数.
试题解析:
(1)解:设白球的个数为x个,
根据题意得:
解得:x=6小明可估计口袋中的白球的个数是6个.
(2)1200× =720.
答:需准备720个红球.
点睛:本题主要考查了用样本估计总体,其本质是利用概率相等来解决问题,如口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,随机摸出一个,摸出白球的概率与重复100次摸到40次白球的概率相同,从而列方程求解.
24.(1)一样大 (2)奇数 (3)大于-3 (4)一样大 (5)绝对值小于6
【分析】一般地,不确定事件发生的可能性是有大小的.而决定不确定事件可能性
大小的因素如下:
①事件发生的可能性大小是由发生事件的条件来决定的;
②可能性的大小与数量的多少有关:数量多,可能性大;数量少,可能性小.
如本题第(1)问中,正数有5个,负数有5个,故抽到正数和负数的可能性一样大.
【详解】解:(1)一样大 (2)奇数 (3)大于-3 (4)一样大 (5)绝对值小于6
【点睛】本题主要考查决定不确定事件可能性大小的因素.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第四章概率
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有以下3个条件:①AC=AB,②AB∥CD,③∠1=∠2,从这3个条件中任选2个作为题设,另1个作为结论,则组成的命题是真命题的概率是( )
A.0 B. C. D.1
2.某班体育委员的抽屉里有5个乒乓球,其中有三个是白色的,两个是黄色的,上体育课的时候,他随手从抽屉里同时拿了两个乒乓球,则他所拿的乒乓球恰好一个白色一个黄色的概率为( ).
A. B. C. D.
3.下列四个命题中,真命题是( )
A.“任意四边形内角和为360°”是不可能事件
B.“湘潭市明天会下雨”是必然事件
C.“预计本题的正确率是95%”表示100位考生中一定有95人做对
D.抛掷一枚质地均匀的硬币,正面朝上的概率是
4.学校给同学们准备了亚运吉祥物“琼琼、宸宸、莲莲”.设同学选择任意一种吉祥物的机会均等.小聪和小慧可以从三种吉祥物中任选一件,则小聪和小慧拿到同一种吉祥物的概率是( )
A. B. C. D.
5.一个不透明袋子中有3个黑球,5个白球,这些球除颜色外无其它差别.从袋子中随机取出1个球,下列说法正确的是( )
A.能够事先确定取出球的颜色 B.取到黑球的可能性更大
C.取到黑球和取到白球的可能性一样大 D.取到白球的可能性更大
6.“明天下雨的概率是”,下列说法正确的是( )
A.明天一定下雨 B.明天一定不下雨
C.明天的地方下雨 D.明天下雨的可能性比较大
7.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为( )
A.20 B.30 C.40 D.50
8.一个布袋里放有红色、黄色、黑色三种球,它们除颜色外其余都相同,红球、黄球、黑球的个数之比为5:3:1,则从布袋里任意摸出一个球是黄球的概率是( )
A. B. C. D.
9.下列事件是随机事件的是( )
A.通常情况温度降到0℃以下,纯净的水结冰;
B.随意翻到一本书的某页,这页的页码是偶数;
C.度量三角形的内角和,结果是360°;
D.测量某天的最低气温,结果为-180℃.
10.小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )
A. B. C. D.
11.在一次抽奖中,若抽中的概率是0.34,则抽不中的概率是( )
A.0.34 B.0.17 C.0.66 D.0.76
12.如图,是一个可以自由转动的转盘,它被分成三个面积相等的扇形,任意转动转盘两次,当转盘停止后,指针所指颜色相同的概率为( )
A. B. C. D.
二、填空题
13.同时投掷两个骰子,它们点数之和不大于4的概率是 .
14.质地均匀的正四面体骰子的四个面上分别写有数字:2,3,4,5.投掷这个正四面体两次,则第一次底面上的数字能够整除第二次底面上的数字的概率是
15.做重复实验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率为 .
16.在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到一个 可以估计这个事件发生的概率.
17.从一副扑克牌(除去大、小王)中任抽一张,则抽到红心的概率为 ;抽到黑桃的概率为 ;抽到红心3的概率为 .
三、解答题
18.小明和小刚用如图所示的两个转盘做配紫色游戏,游戏规则是:分别旋转两个转盘,若其中一个转盘转出了红色,另一个转出了蓝色则可以配成紫色.此时小刚得1分,否则小明得1分.这个游戏规则对双方公平吗?请说明理由.若你认为不公平,如何修改规则才能使游戏对双方公平?
19.甲、乙两同学用一副扑克牌中牌面数字分别是3、4、5、6的4张牌做抽数学游戏.游戏规则是:将这4张牌的正面全部朝下,洗匀,从中随机抽取一张,抽得的数作为十位上的数字,然后,将所抽的牌放回,正面全部朝下、洗匀,再从中随机抽取一张,抽得的数作为个位上的数字,这样就得到一个两位数.若这个两位数小于45,则甲获胜,否则乙获胜.你认为这个游戏公平吗?请运用概率知识说明理由.
20.家乐福超市“端午节”举行有奖促销活动:凡一次性购物满200元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被分成16等分,摇中红、黄、蓝色区域,分获一、二、三等奖,奖金依次为48元、40元、32元.一次性购物满200元者,如果不摇奖可返还现金15元.
(1)摇奖一次,获一等奖的概率是多少?
(2)小明一次性购物满了200元,他是参与摇奖划算还是领15元现金划算,请你帮他算算.
21.对某篮球运动员进行3分球投篮测试结果如表所示:
投篮次数 10 50 100 150 200
命中次数 4 25 65 90 120
命中率
(1)计算表中投篮50次、100次、150次、200次相应的命中率;
(2)这个运动员3分球投篮命中的概率约是多少?
(3)估计这个运动员3分球投篮30次能得多少分.
22.如图所示,甲、乙两人在玩转盘游戏时,分别把转盘A,B分成3等份和1等份,并在每一份内标上数字.游戏规则:同时转动两个转盘,当转盘停止后,指针所在区域的数字之积为奇数时,甲获胜;当数字之积为偶数时,乙获胜.如果指针恰好在分割线上时,则需重新转动转盘.
(1)利用画树状图或列表的方法,求甲获胜的概率.
(2)这个游戏规则对甲、乙双方公平吗?若公平,请说明理由;若不公平,请你在转盘A上只修改一个数字使游戏公平(不需要说明理由).
23.一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球?
24.在一个口袋里有大小形状都一样的10张卡片,分别写有-1,-2,-3,-4,-5,1,2,3,4,5.从中任意抽出一张卡片.
(1)抽到正数的可能性大还是抽到负数的可能性大?
(2)抽到奇数的可能性大还是抽到偶数的可能性大?
(3)抽到小于2的可能性大还是抽到大于-3的可能性大?
(4)抽到平方数的可能性大还是抽到立方数的可能性大?
(5)抽到绝对值大于1的可能性大还是抽到绝对值小于6的可能性大?
《第四章概率》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D A D C D D A B B C
题号 11 12
答案 C A
1.D
【分析】根据题意找出组成命题的所有等可能的情况数,找出组成的命题是真命题的情况数,即可求出所求的概率.
【详解】所有等可能的情况有3种,分别为①② ③;①③ ②;②③ ①,其中组成命题是真命题的情况有:①② ③;①③ ②;②③ ①,则P=1.
故选D.
【点睛】本题考查了用列举法求概率,平行线的性质与判定,等腰三角形的判定与性质,以及命题与定理,弄清题意是解答本题的关键.
2.A
【分析】本题考查的是利用画树状图或列表法求解随机事件的概率,先列表得到所有等可能的结果数有20种,所拿的乒乓球恰好一个白色一个黄色的情况有:种,再利用概率公式计算即可.
【详解】解:用,,表示三个白色乒乓球, ,表示两个黄色的乒乓球,
列表如下:
所有等可能的结果数有20种,他所拿的乒乓球恰好一个白色一个黄色的情况有:种,
∴恰好一个白色一个黄色的概率为.
故选A
3.D
【详解】试题分析:A.“任意四边形内角和为360°”是必然事件,错误;
B.“湘潭市明天会下雨”是随机事件,错误;
C.“预计本题的正确率是95%”表示100位考生中不一定有95人做对,错误;
D.抛掷一枚质地均匀的硬币,正面朝上的概率是,正确.
故选D.
考点:命题与定理.
4.C
【分析】画树状图展示所有9种等可能的情况数.找出符合条件的情况数,然后根据概率公式求解即可.
【详解】解:画树状图为:
共有9种等可能的情况数.其中小聪和小慧拿到同一种吉祥物的有3种情况,
则小聪和小慧拿到同一种吉祥物的概率是.
故选:C.
【点睛】本题考查的列表法与树状补法利用列表或树状图法展示所有或树状图法展示所有可能的结果,求出n.再从中选出符合事件a或b的结果数目m.然后根据概率公式计算事件a或事件b的概率
5.D
【分析】根据不同颜色的球的数量确定摸到哪种球的可能性的大小后即可确定正确的选项
【详解】解:不透明袋子中有3个黑球、5个白球,这些球除颜色外其它无差别,
白球数量大于黑球数量,其摸球具有随机性,
摸到白球的可能性大于摸到黑球的可能性,
故选D
【点睛】本题考查了可能性的大小的知识,哪种球的数量大,摸到这种球的可能性就大
6.D
【分析】本题考查了概率的意义,解决本题的关键是理解概率表示随机事件发生的可能性大小;
根据概率的意义找到正确选项即可.
【详解】解:明天下雨的概率是,说明明天下雨的可能性比较大.所以只有D合题意.
故选:D.
7.A
【详解】分析:根据白球的频率稳定在0.4附近得到白球的概率约为0.4,根据白球个数确定出总个数,进而确定出黑球个数n.
详解:根据题意得: ,
计算得出:n=20,
故选A.
点睛:根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.
8.B
【详解】分析:用黄球所占的份数除以所有份数的和即可求得是黄球的概率.
详解:∵红球、黄球、黑球的个数之比为5:3:1,
∴从布袋里任意摸出一个球是黄球的概率是.
故选B.
点睛:此题考查了概率公式的应用.注意用到的知识点为:概率=所求情况数与总情况数之比.
9.B
【详解】试题分析:一个概率事件分为:确定事件(包括:必然事件与不可能事件)和随机事件.必然事件发生的可能性是“1”,不可能事件发生的可能性是“0”,随机事件发生的可能性为“0~1”之间.据此可以判断答案B是正确的.
试题解析:A.通常情况温度降到0℃以下,纯净的水结冰,这是一个必然事件,发生的可能性是“1”;
B.随意翻到一本书的某页,这页的页码是偶数,这是一个不确定事件,发生的可能性是“0.5”;这页的页码也可能是奇数;
C.度量三角形的内角和,结果是360°,这是一个不可能事件,发生的可能性是“0”;三角形内角和为180°;
D.测量某天的最低气温,结果为-180°,这是一个不可能事件,发生的可能性是“0”.
故选B.
考点:随机事件.
10.C
【分析】利用列表法或树状图即可解决.
【详解】分别用r、b代表红色帽子、黑色帽子,用R、B、W分别代表红色围巾、黑色围巾、白色围巾,列表如下:
R B W
r rR rB rW
b bR bB bW
则所有可能的结果数为6种,其中恰好为红色帽子和红色围巾的结果数为1种,根据概率公式,恰好为红色帽子和红色围巾的概率是.
故选:C.
【点睛】本题考查了简单事件的概率,常用列表法或画树状图来求解.
11.C
【详解】在一次抽奖中,抽中的概率和抽不中的概率之和是1,抽中的概率是0.34,则抽不中的概率是1-0.34=0.66,故选C.
12.A
【详解】列表得:
红 黄 蓝
红 (红,红) (黄,红) (蓝,红)
黄 (红,黄) (黄,黄) (蓝,黄)
蓝 (红,蓝) (黄,蓝) (蓝,蓝)
由表格可知,所有等可能的情况数有9种,其中颜色相同的情况有3种,则任意转动转盘两次,当转盘停止后,指针所指颜色相同的概率为 .故选A.
13.
【详解】试题分析:根据题意,设第一颗骰子的点数为x,第二颗骰子的点数为y,用(x,y)表示抛掷两个骰子的点数情况,由分步计数原理可得(x,y)的情况数目,由列举法可得其中x+y≤4的情况数目,进而由等可能事件的概率公式计算可得答案.
考点:列表法与树状图法
14.
【详解】试题解析:由树状图
可知共有4×4=16种可能,第一次底面上的数字能够整除第二次底面上的数字的有5种,所以概率是.
故答案为.
15.0.56.
【分析】由于事件“凸面向上”和“凹面向上”是对立事件,根据对立事件的概率和为1计算即可.
【详解】瓶盖只有两面,“凸面向上”的频率约为0.44,
则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为1﹣0.44=0.56,
故答案为0.56.
【点睛】本题主要考查概率的意义、等可能事件的概率,解答此题关键是要明白瓶盖只有两面,即凸面和凹面.
16.常数
【详解】随着实验次数的增加,隐含的规律逐渐显现,事件发生的频率逐渐稳定到某一个数值,所以,我们可以用平稳时的频率去估计这一随机事件在每次实验时发生的机会的大小,在同样条件下,大量重复试验时,根据一个随机事件发生的频率逐渐稳定到一个常数可以估计这个事件发生的概率,故答案为:常数.
17.
【分析】根据题意可得:这幅牌中共有52张,其中到红心13张,黑桃13张,红心3只有1张,故从中任抽一张,抽到红心的概率为,抽到黑桃的概率为;抽到红心3的概率为.
【详解】抽到红心的概率为,抽到黑桃的概率为;抽到红心3的概率为.
故答案为:;;.
【点睛】本题考查了概率的求法.如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A).
18.见解析
【详解】解:根据题意,列表得:
,,
所以小刚得1分的概率为,小明得1分的概率为,
因为,所以游戏对双方不公平.
修改方法不唯一,
若其中一个转盘转出红色,另一个转盘转出了蓝色,则可以配成紫色,此时小刚得7分,否则小明得2分.
也可以修改规则,若其中一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色,此时小刚得1分;若两个转盘转出的颜色相同,则小明得1分;否则两人均不得分.
故答案为:不公平,修改方式见上面解析.
红 白 蓝
红 (红,红) (红,白) (红,蓝)
黄 (黄,红) (黄,白) (黄,蓝)
蓝 (蓝,红) (蓝,白) (蓝,蓝)
19.不公平,理由见解析.
【分析】游戏是否公平,关键要看是否游戏双方赢的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】解:这个游戏不公平,游戏所有可能出现的结果如下表:
第二次 第一次 3 4 5 6
3 33 34 35 36
4 43 44 45 46
5 53 54 55 56
6 63 64 65 66
表中共有16种等可能结果,小于45的两位数共有6种.
∴
∵
∴这个游戏不公平.
【点睛】本题考查的是游戏公平性的判断.判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平.用到的知识点为:概率=所求情况数与总情况数之比.
20.(1) ;(2) 转转盘划算.
【分析】(1)找到红色区域的份数占总份数的多少即为获得一等奖的概率,
(2)游戏是否合算,关键要看游戏双方获胜的机会是否相等,即判断双方取胜的概率是否相等,或转化为在总情况明确的情况下,判断双方取胜所包含的情况数目是否相等.
【详解】解:(1)整个圆周被分成了16份,红色为1份,
∴获得一等奖的概率为:,
(2)转转盘:元,
∵16元>15元,
∴转转盘划算.
【点睛】本题主要考查了古典型概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=,难度适中.
21.(1);;;
(2)
(3)54分
【分析】本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率;用频率估计概率得到的是近似值,随实验次数的增多,得到的值越来越精确,还考查了频率的计算公式.
(1)用对应的m除以n即可求解;
(2)根据(1)的计算结论可估计这个运动员投篮3分球命中率约为;
(3)根据(2) 的估计得到投篮30次命中次,然后用18乘以3即可.
【详解】(1)解:投篮50次、100次、150次、200次相应的命中率分别为:
;;;;
(2)解:由表格数据知,当投篮次数逐渐增加时,命中率稳定在附近,所以估计这个运动员3分球投篮.
(3)解:由(2)的结论可知这个运动员投篮30次,命中的次数约为(次),约能得到(分).
22.(1)见解析,甲获胜概率为;(2)这个游戏规则对甲、乙双方不公平,将转盘A上的数字2改为1,则游戏公平.
【分析】(1)列表得出所有等可能结果,从中找到符合条件的结果数,再根据概率公式计算可得;
(2)先计算出数字之积为偶数的概率,判断概率是否相等即可得知游戏是否公平.
【详解】解:(1)列表如下:
﹣2 ﹣3 2 3
1 ﹣2 ﹣3 2 3
2 ﹣4 ﹣6 4 6
3 ﹣6 ﹣9 6 9
由表可知,共有12种等可能结果,其中指针所在区域的数字之积为奇数的有4种结果,
所以甲获胜概率为;
(2)∵指针所在区域的数字之积为偶数的概率为,
∴这个游戏规则对甲、乙双方不公平,
将转盘A上的数字2改为1,则游戏公平.
【点睛】此题考查了游戏的公平性,判断游戏公平性就要计算每个事件的概率,概率相等就公平,否则就不公平,用到的知识点为:概率=所求情况数与总情况数之比.
23.(1)小明可估计口袋中的白球的个数是6个.
(2)需准备720个红球.
【详解】试题分析:
(1)用白球的个数:(白球的个数+红球的个数)=40:100,列方程求解;
(2)用彩球的总数乘以,即可得到红球的个数.
试题解析:
(1)解:设白球的个数为x个,
根据题意得:
解得:x=6小明可估计口袋中的白球的个数是6个.
(2)1200× =720.
答:需准备720个红球.
点睛:本题主要考查了用样本估计总体,其本质是利用概率相等来解决问题,如口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,随机摸出一个,摸出白球的概率与重复100次摸到40次白球的概率相同,从而列方程求解.
24.(1)一样大 (2)奇数 (3)大于-3 (4)一样大 (5)绝对值小于6
【分析】一般地,不确定事件发生的可能性是有大小的.而决定不确定事件可能性
大小的因素如下:
①事件发生的可能性大小是由发生事件的条件来决定的;
②可能性的大小与数量的多少有关:数量多,可能性大;数量少,可能性小.
如本题第(1)问中,正数有5个,负数有5个,故抽到正数和负数的可能性一样大.
【详解】解:(1)一样大 (2)奇数 (3)大于-3 (4)一样大 (5)绝对值小于6
【点睛】本题主要考查决定不确定事件可能性大小的因素.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
