2.2圆心角、圆周角同步练习(含解析)
图片预览

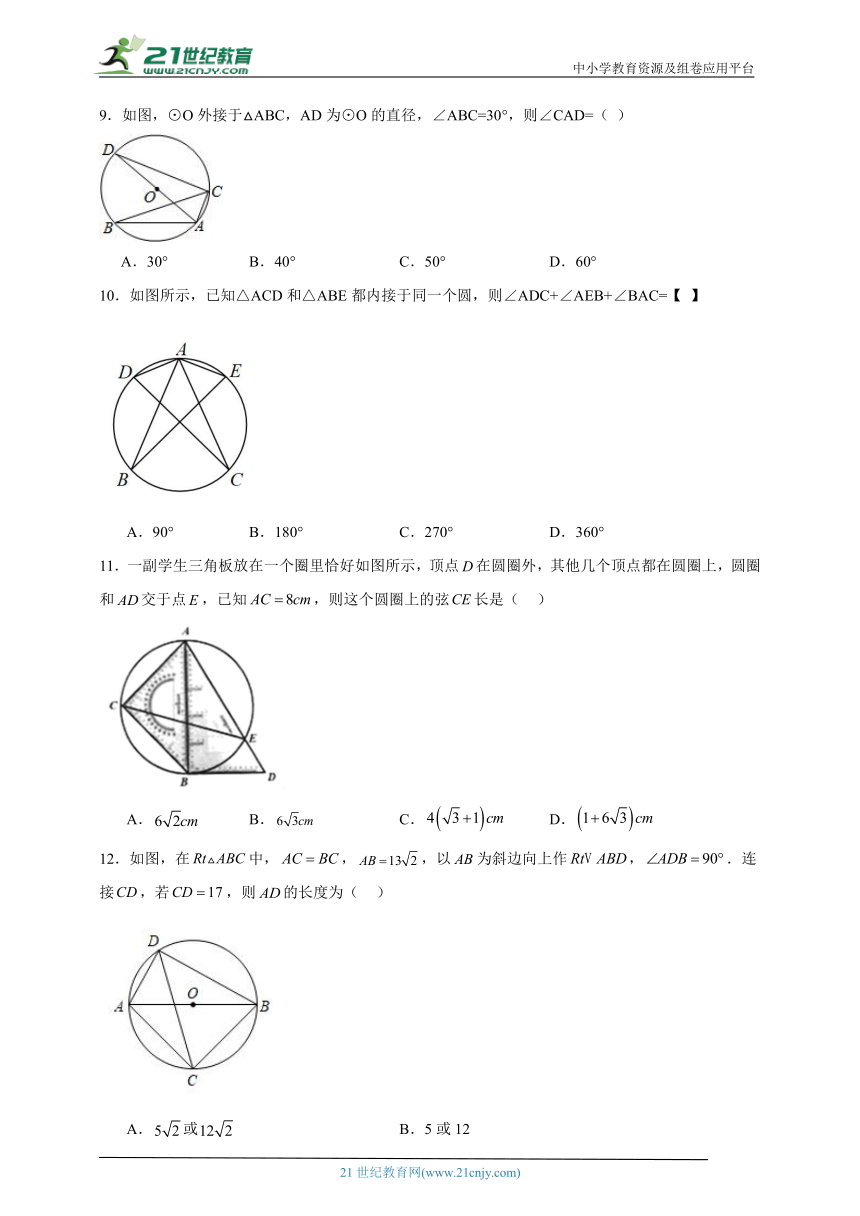

文档简介
中小学教育资源及组卷应用平台
2.2圆心角、圆周角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB为⊙O的直径,点C、D在⊙O上,若∠AOD=30°,则∠BCD的度数是( )
A.150° B.120° C.105° D.75°
2.如图,AB、AC是⊙O的两条弦,∠A=35°,过C点的切线与OB的延长线交于点D,则∠D的度数为( )
A.20° B.30° C.35° D.40°
3.如图,四边形内接于圆O,E为延长线上一点,若,则的度数为( )
A. B. C. D.
4.如图所示,四边形的四个顶点都在上,称这样的四边形为圆内接四边形,则图中( )
A. B. C. D.
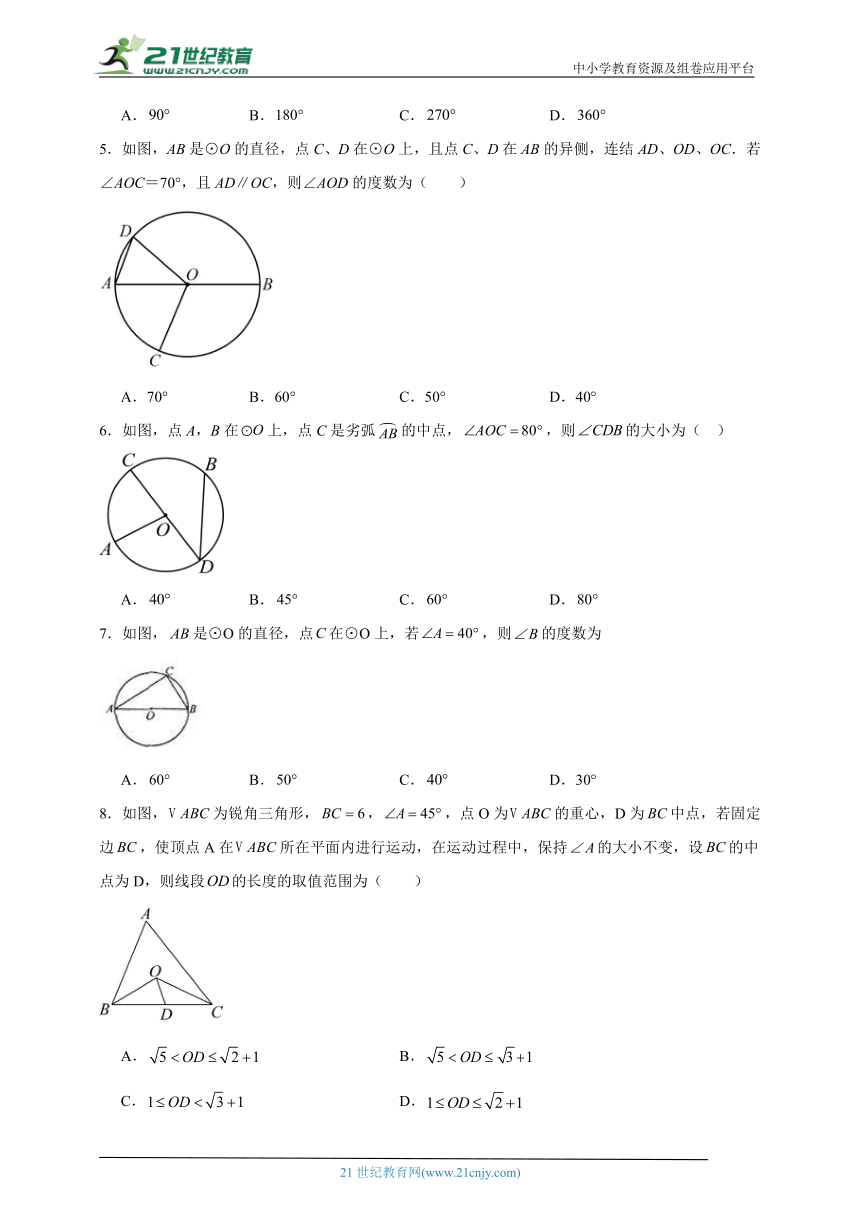
5.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
6.如图,点A,B在上,点C是劣弧的中点,,则的大小为( )
A. B. C. D.
7.如图,是⊙O的直径,点在⊙O上,若,则的度数为
A. B. C. D.30°
8.如图,为锐角三角形,,,点O为的重心,D为中点,若固定边,使顶点A在所在平面内进行运动,在运动过程中,保持的大小不变,设的中点为D,则线段的长度的取值范围为( )
A. B.
C. D.
9.如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A.30° B.40° C.50° D.60°
10.如图所示,已知△ACD和△ABE都内接于同一个圆,则∠ADC+∠AEB+∠BAC=【 】
A.90° B.180° C.270° D.360°
11.一副学生三角板放在一个圈里恰好如图所示,顶点在圆圈外,其他几个顶点都在圆圈上,圆圈和交于点,已知,则这个圆圈上的弦长是( )
A. B. C. D.
12.如图,在中,,,以为斜边向上作,.连接,若,则的长度为( )
A.或 B.5或12
C.或 D.5或10
二、填空题
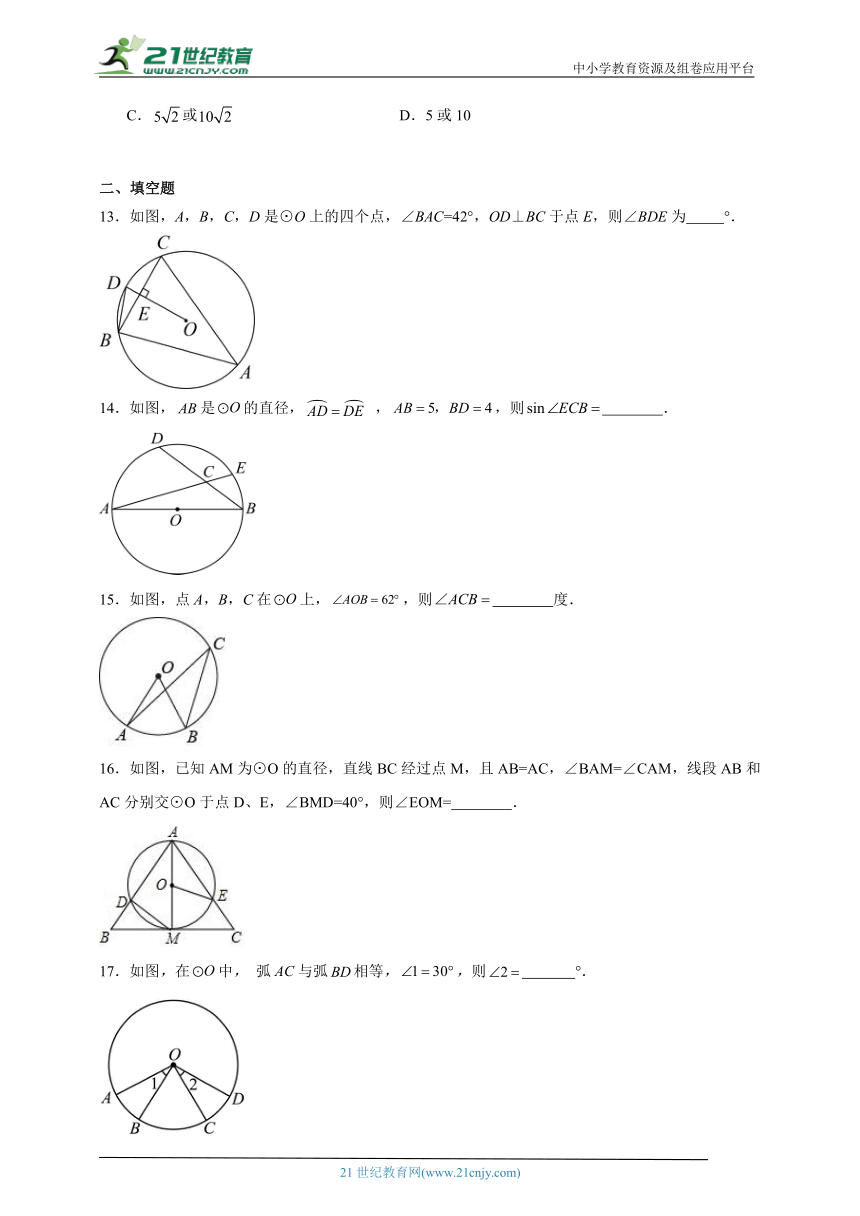
13.如图,A,B,C,D是⊙O上的四个点,∠BAC=42°,OD⊥BC于点E,则∠BDE为 °.
14.如图,是的直径, ,,则 .
15.如图,点A,B,C在上,,则 度.
16.如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM= .
17.如图,在中, 弧与弧相等,,则 °.
三、解答题
18.如图是半径为2的圆,
(1)在其中画两个不重叠的扇形AOB和扇形BOC,使扇形AOB的圆心角为120度,扇形BOC的圆心角为90度,
(2)求第三个扇形AOC的面积.
19.已知AB是⊙O的直径.
(1)如图①,,∠MON=35°,求∠AON的大小;
(2)如图②,E,F是⊙O上的两个点,AD⊥EF于点D,若∠DAE=20°,求∠BAF的大小.
20.已知:如图,内接于,平分交于点M,于D.求证:.
21.如图,四边形内接于一圆,是边的延长线.
(1)求证;
(2)若,,求的度数.
22.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
23.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这种设计的合理性.
24.如图,⊙O中弦AB=CD,且AB与CD交于E.
求证:DE=AE.
《2.2圆心角、圆周角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D A B D D B
题号 11 12
答案 C A
1.C
【详解】试题解析:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AOD=30°,
∴∠ACD=15°,
∴∠BCD=∠ACB+∠ACD=105°,
故选C.
2.A
【分析】由于CD是切线,可知∠OCD=90°,而∠A=35°,利用圆周角定理可求∠COD,进而可求∠D.
【详解】连接OC,
∵CD是切线,
∴∠OCD=90°,
∵∠A=35°,
∴∠COD=2∠A=70°,
∴∠D=90° 70°=20°.
故选A.
【点睛】本题考查的是圆,熟练掌握切线的性质是解题的关键.
3.B
【分析】根据圆内接四边形的性质得出,再由同角的补角相等即可得出结果.本题主要考查了圆内接四边形的性质,熟知圆内接四边形的对角互补是解决此题的关键.
【详解】解:∵四边形是圆内接四边形,
∴,
又,
∴,
故选:B.
4.B
【分析】先证明:∠DAC+∠ACD=∠DBC+∠ABD=∠ABC,再利用三角形的内角和定理可得: 再利用四边形的内角和可得答案.
【详解】由圆内接四边形对角互补得.
证明:
连接AC、BD
∵∠DAC=∠DBC,∠ACD=∠ABD(同弧所对的圆周角相等)
∴∠DAC+∠ACD=∠DBC+∠ABD=∠ABC
∵∠DAC+∠ACD+∠ADC=180°(三角形内角和180°)
∴∠ABC+∠ADC=180°
故选B
【点睛】本题考查圆内接四边形对角互补的知识点,牢记定理是解题关键.
5.D
【分析】首先由AD∥OC可以得到∠AOC=∠DAO,又由OD=OA得到∠ADO=∠DAO,由此即可求出∠AOD的度数.
【详解】解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180-70°-70°=40°.
故选:D.
【点睛】本题主要考查平行线的性质,等腰三角形的判定和性质及圆的基本性质,由半径相等得到∠ADO=∠DAO是解题的关键.
6.A
【分析】此题考查圆周角定理,由点是劣弧的中点,得到,根据圆周角定理即可得到结论.
【详解】解:∵点C是劣弧的中点,
∴,
∴,
∵,
∴,
故选:A.
7.B
【详解】∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=40°,
∴∠B=90°-∠A=50°.
故选B
8.D
【分析】如图,作的外接圆,点为圆心,,根据重心定理,得出,根据圆周角定理,得出,进而得出,再根据等角对等边,得出,再根据勾股定理,得出,,当时,最长,可求此时最大值,由于,可得此时最小值,进而可得的取值范围.
【详解】解:如图,作的外接圆,点为圆心,,
∵点O为的重心,
∴,
∵,
∴,
∴,
∴,由勾股定理知,
∴,
∵当时,最长,
∴最大值为,
∵,
∴,
∴.
故选:D
【点睛】本题考查了三角形的外接圆、重心定理、圆周角定理、等角对等边、勾股定理等知识,解题的关键在于熟练掌握外接圆.重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍.该点叫做三角形的重心.
9.D
【分析】首先由∠ABC=30°,推出∠ADC=30°,然后根据AD为⊙O的直径,推出∠DCA=90°,最后根据直角三角形的性质即可推出∠CAD=90°-∠ADC,通过计算即可求出结果.
【详解】解:∵∠ABC=30°,
∴∠ADC=30°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°-30°=60°.
故选D.
【点睛】本题主要考查圆周角定理,直角三角形的性质,角的计算,关键在于通过相关的性质定理推出∠ADC和∠DCA的度数.
10.B
【详解】∵∠ADC,∠AEB,∠BAC所对圆弧正好是一个圆周,
∴∠ADC+∠AEB+∠BAC=180°.故选B.
11.C
【分析】作于点E,连接BE,在中求出EF的长,在中求出CF的长,即可求出CE的长.
【详解】解:如图,作于点E,连接BE,
∵是等腰直角三角形,,
∴,,,
∴,AB是直径,
∴,
∵是含的三角板,
∴,
∴,,,
∴
在中,,,
∴,
在中,,,
∴CF=4,
∴=.
故选C.
【点睛】本题考查了圆周角定理及勾股定理,能够把求CE长度问题转化直角三角形中的计算问题是解题的关键.
12.A
【分析】分两种情况讨论,当时,或当时,画出相应的图形,延长至点,使,作于点,证明,根据全等三角形的性质
得到,继而证明为等腰直角三角形,再由勾股定理解得,最后根据线段的和差解题即可.
【详解】解:当时,如图,延长至点,使,作于点,
中,
在与中,
为等腰直角三角形,
;
当时,如图,
延长至点,使,作于点,
中,
在与中,
为等腰直角三角形,
;
综上所述,的长度为或,
故选:A.
【点睛】本题考查全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识,是重要考点,难度一般,掌握相关知识是解题关键.
13.69
【分析】连接CD,由圆内接四边形的性质得∠BDC+∠BAC=180°,可得∠BDC =180°-42°=138°,再由垂径定理得出,则BD=CD,然后根据等腰三角形的性质即可求出∠BDE的度数.
【详解】解:如图,连接CD,
∵A,B,C,D是⊙O上的四个点,
∴∠BDC+∠BAC=180°,
∵∠BAC=42°,
∴∠BDC =180°-42°=138°,
∵OD⊥BC,
∴,
∴BD=CD,
∴∠BDE=∠BDC=,
故答案为:69.
【点睛】本题考查的是圆内接四边形的性质及垂径定理等知识,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14./0.8
【分析】本题考查了圆周角定理,解直角三角形,以及勾股定理等知识.掌握圆周角的两个定理:①在同圆或等圆中,同弧或等弧所对的圆周角相等.②半圆(或直径)所对的圆周角是直角;
连接,根据直径所对的圆周角是直角,构建两个直角三角形,再利用等弧所对的圆周角相等得:,最后利用等角的三角函数得出结论.
【详解】解:连接,
∵是的直径,
∴,
在中,,
∴,
∵,
∴.
∴.
∴,
∴.
∴.
∴.
故答案为:
15.31
【分析】根据圆周角定理进行求解即可;
【详解】解:由圆周角定理可知:
故答案为:31.
【点睛】本题主要考查圆周角定理,掌握圆周角定理是解题的关键.
16.80°
【详解】解:连接EM,
∵AB=AC,∠BAM=∠CAM,∴AM⊥BC,
∵AM为⊙O的直径,∴∠ADM=∠AEM=90°,
∴∠AME=∠AMD=90°﹣∠BMD=50°∴∠EAM=40°,
∴∠EOM=2∠EAM=80°,
故答案为80°.
【点睛】本题考查圆周角定理.
17.30
【分析】由弧与弧相等推得弧和弧相等,再根据在同圆中,等弧所对的圆周角相等,从而求出的度数.
【详解】解:∵弧与弧相等,
∴弧和弧相等,
∴;
故答案为:30.
【点睛】本题考查圆心角、弧、弦的关系,熟练掌握等弧所对的圆周角相等是解题的关键.
18.(1)作图见解析;(2)
【分析】(1)根据扇形定义及题目要求画出即可;
(2)根据扇形的面积公式计算即可.
【详解】解:(1)如图所示:
(2),,
,
故.
【点睛】本题考查的是扇形面积的计算,解题的关键是根据题意求出对应圆心角度数是前提,掌握扇形的面积公式.
19.(1)75°;(2)20°
【分析】(1)根据圆心角、弧、弦之间的关系求出∠MON=∠MOC=∠BOC=35°,再求出答案即可;
(2)根据三角形外角性质求出∠AEF,根据圆内接四边形的性质得出∠AEF+∠ABF=180°,求出∠ABF,根据圆周角定理求出∠AFB=90°,再根据三角形内角和定理求出即可.
【详解】解:(1)∵,∠MON=35°,
∴∠MON=∠MOC=∠BOC=35°,
∴∠AON=180°﹣∠MON﹣∠MOC﹣∠BOC=180°﹣35°﹣35°﹣35°=75°;
(2)连接BF,
∵AD⊥直线,
∴∠ADE=90°,
∵∠DAE=20°,
∴∠AEF=∠ADE+∠DAE=110°,
∵四边形为圆内接四边形,
∴∠ABF+∠AEF=180°,
∴∠ABF=70°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=180°﹣∠AFB﹣∠ABF=20°.
【点睛】本题考查的是圆心角与弧之间的关系,圆的内接四边形的性质,圆周角定理,掌握以上知识是解题的关键.
20.见解析.
【分析】首先延长AO交⊙O于N,连接BN,根据圆周角定理与AD⊥BC,可得∠ABN=∠ADC=90°,又由∠C=∠N,可得∠BAN=∠DAC,然后根据AM平分∠BAC,即可证得∠MAO=∠MAD.
【详解】证明:延长AO交⊙O于N,连接BN,
∵AN是⊙O的直径,AD⊥BC,
∴∠ABN=∠ADC=90°,
∴∠BAN+∠N=90°,∠DAC+∠C=90°,
∵∠N=∠C,
∴∠BAN=∠DAC,
∵AM平分∠BAC, 即∠BAM=∠CAM,
∴∠MAO=∠MAD.
【点睛】本题主要考查了圆周角定理以及角平分线的定义,解题的关键是准确作出辅助线,掌握圆周角定理的应用.
21.(1)见解析
(2)
【分析】(1)根据圆内接四边形的性质得到,根据同角的补角相等证明结论;
(2)根据圆周角定理得到,根据三角形内角和定理计算即可.
【详解】(1)证明:四边形内接于圆,
,
,
;
(2)解:,
,
.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,解题的关键是掌握圆内接四边形的对角互补.
22.(1)∠A=90°﹣α;(2)∠A=60°.
【分析】(1)根据圆内接四边形的性质得到∠A=∠BCF,再利用三角形外角性质得∠EBF=∠A+∠E,由三角形内角和定理得∠EBF=180°-∠BCF-∠F,所以∠A+∠E=180-∠A-∠F,然后利用∠E+∠F=α可得∠A=90°-α;
(2)利用(1)中的结论进行计算.
【详解】(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
【点睛】本题考查了圆内接四边形的性质:圆内接四边形的对角互补;圆内接四边形的任意一个外角等于它的内对角.
23.见解析
【分析】根据题意画出示意图,其中BC表示电影幕的宽,G、I分别为圆弧形排列的座位中的任意两个,根据图形可知∠BGC、∠BJC分别为两个座位的视角,由此结合圆周角定理的推论求解即可.
【详解】根据题意画出图形,BC表示电影幕的宽,
由同弧所对圆周角相等可知∠BGC=∠BJC,即同排的观众视角相等.
【点睛】本题是圆周角定理的推论在实际问题中的应用,解题的关键是要理解在同排的观众视角需相同.
24.见解析
【分析】连接AD,由于AB=CD,所以 ,从而得到,再根据同弧所对的圆周角相等得到∠BAD=∠CDA,最后由等角对等边证得DE=AE.
【详解】解:证明:连接AD,
∵AB=CD,
∴ ,
∴,
即 ,
∴∠BAD=∠CDA,
∴DE=AE(等角对等边).
【点睛】本题考查了在同圆中,圆周角、弧、弦的关系及等腰三角形的判定,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.2圆心角、圆周角
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,AB为⊙O的直径,点C、D在⊙O上,若∠AOD=30°,则∠BCD的度数是( )
A.150° B.120° C.105° D.75°
2.如图,AB、AC是⊙O的两条弦,∠A=35°,过C点的切线与OB的延长线交于点D,则∠D的度数为( )
A.20° B.30° C.35° D.40°
3.如图,四边形内接于圆O,E为延长线上一点,若,则的度数为( )
A. B. C. D.
4.如图所示,四边形的四个顶点都在上,称这样的四边形为圆内接四边形,则图中( )
A. B. C. D.
5.如图,AB是⊙O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连结AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
6.如图,点A,B在上,点C是劣弧的中点,,则的大小为( )
A. B. C. D.
7.如图,是⊙O的直径,点在⊙O上,若,则的度数为
A. B. C. D.30°
8.如图,为锐角三角形,,,点O为的重心,D为中点,若固定边,使顶点A在所在平面内进行运动,在运动过程中,保持的大小不变,设的中点为D,则线段的长度的取值范围为( )
A. B.
C. D.
9.如图,⊙O外接于△ABC,AD为⊙O的直径,∠ABC=30°,则∠CAD=( )
A.30° B.40° C.50° D.60°
10.如图所示,已知△ACD和△ABE都内接于同一个圆,则∠ADC+∠AEB+∠BAC=【 】
A.90° B.180° C.270° D.360°
11.一副学生三角板放在一个圈里恰好如图所示,顶点在圆圈外,其他几个顶点都在圆圈上,圆圈和交于点,已知,则这个圆圈上的弦长是( )
A. B. C. D.
12.如图,在中,,,以为斜边向上作,.连接,若,则的长度为( )
A.或 B.5或12
C.或 D.5或10
二、填空题
13.如图,A,B,C,D是⊙O上的四个点,∠BAC=42°,OD⊥BC于点E,则∠BDE为 °.
14.如图,是的直径, ,,则 .
15.如图,点A,B,C在上,,则 度.
16.如图,已知AM为⊙O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交⊙O于点D、E,∠BMD=40°,则∠EOM= .
17.如图,在中, 弧与弧相等,,则 °.
三、解答题
18.如图是半径为2的圆,
(1)在其中画两个不重叠的扇形AOB和扇形BOC,使扇形AOB的圆心角为120度,扇形BOC的圆心角为90度,
(2)求第三个扇形AOC的面积.
19.已知AB是⊙O的直径.
(1)如图①,,∠MON=35°,求∠AON的大小;
(2)如图②,E,F是⊙O上的两个点,AD⊥EF于点D,若∠DAE=20°,求∠BAF的大小.
20.已知:如图,内接于,平分交于点M,于D.求证:.
21.如图,四边形内接于一圆,是边的延长线.
(1)求证;
(2)若,,求的度数.
22.如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E,F.
(1)若∠E+∠F=α,求∠A的度数(用含α的式子表示);
(2)若∠E+∠F=60°,求∠A的度数.
23.为什么有些电影院的座位排列(横排)呈圆弧形?说一说这种设计的合理性.
24.如图,⊙O中弦AB=CD,且AB与CD交于E.
求证:DE=AE.
《2.2圆心角、圆周角》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B D A B D D B
题号 11 12
答案 C A
1.C
【详解】试题解析:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AOD=30°,
∴∠ACD=15°,
∴∠BCD=∠ACB+∠ACD=105°,
故选C.
2.A
【分析】由于CD是切线,可知∠OCD=90°,而∠A=35°,利用圆周角定理可求∠COD,进而可求∠D.
【详解】连接OC,
∵CD是切线,
∴∠OCD=90°,
∵∠A=35°,
∴∠COD=2∠A=70°,
∴∠D=90° 70°=20°.
故选A.
【点睛】本题考查的是圆,熟练掌握切线的性质是解题的关键.
3.B
【分析】根据圆内接四边形的性质得出,再由同角的补角相等即可得出结果.本题主要考查了圆内接四边形的性质,熟知圆内接四边形的对角互补是解决此题的关键.
【详解】解:∵四边形是圆内接四边形,
∴,
又,
∴,
故选:B.
4.B
【分析】先证明:∠DAC+∠ACD=∠DBC+∠ABD=∠ABC,再利用三角形的内角和定理可得: 再利用四边形的内角和可得答案.
【详解】由圆内接四边形对角互补得.
证明:
连接AC、BD
∵∠DAC=∠DBC,∠ACD=∠ABD(同弧所对的圆周角相等)
∴∠DAC+∠ACD=∠DBC+∠ABD=∠ABC
∵∠DAC+∠ACD+∠ADC=180°(三角形内角和180°)
∴∠ABC+∠ADC=180°
故选B
【点睛】本题考查圆内接四边形对角互补的知识点,牢记定理是解题关键.
5.D
【分析】首先由AD∥OC可以得到∠AOC=∠DAO,又由OD=OA得到∠ADO=∠DAO,由此即可求出∠AOD的度数.
【详解】解:∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180-70°-70°=40°.
故选:D.
【点睛】本题主要考查平行线的性质,等腰三角形的判定和性质及圆的基本性质,由半径相等得到∠ADO=∠DAO是解题的关键.
6.A
【分析】此题考查圆周角定理,由点是劣弧的中点,得到,根据圆周角定理即可得到结论.
【详解】解:∵点C是劣弧的中点,
∴,
∴,
∵,
∴,
故选:A.
7.B
【详解】∵AB是⊙O的直径,
∴∠C=90°,
∵∠A=40°,
∴∠B=90°-∠A=50°.
故选B
8.D
【分析】如图,作的外接圆,点为圆心,,根据重心定理,得出,根据圆周角定理,得出,进而得出,再根据等角对等边,得出,再根据勾股定理,得出,,当时,最长,可求此时最大值,由于,可得此时最小值,进而可得的取值范围.
【详解】解:如图,作的外接圆,点为圆心,,
∵点O为的重心,
∴,
∵,
∴,
∴,
∴,由勾股定理知,
∴,
∵当时,最长,
∴最大值为,
∵,
∴,
∴.
故选:D
【点睛】本题考查了三角形的外接圆、重心定理、圆周角定理、等角对等边、勾股定理等知识,解题的关键在于熟练掌握外接圆.重心定理:三角形的三条中线交于一点,这点到顶点的距离是它到对边中点距离的2倍.该点叫做三角形的重心.
9.D
【分析】首先由∠ABC=30°,推出∠ADC=30°,然后根据AD为⊙O的直径,推出∠DCA=90°,最后根据直角三角形的性质即可推出∠CAD=90°-∠ADC,通过计算即可求出结果.
【详解】解:∵∠ABC=30°,
∴∠ADC=30°,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠CAD=90°-30°=60°.
故选D.
【点睛】本题主要考查圆周角定理,直角三角形的性质,角的计算,关键在于通过相关的性质定理推出∠ADC和∠DCA的度数.
10.B
【详解】∵∠ADC,∠AEB,∠BAC所对圆弧正好是一个圆周,
∴∠ADC+∠AEB+∠BAC=180°.故选B.
11.C
【分析】作于点E,连接BE,在中求出EF的长,在中求出CF的长,即可求出CE的长.
【详解】解:如图,作于点E,连接BE,
∵是等腰直角三角形,,
∴,,,
∴,AB是直径,
∴,
∵是含的三角板,
∴,
∴,,,
∴
在中,,,
∴,
在中,,,
∴CF=4,
∴=.
故选C.
【点睛】本题考查了圆周角定理及勾股定理,能够把求CE长度问题转化直角三角形中的计算问题是解题的关键.
12.A
【分析】分两种情况讨论,当时,或当时,画出相应的图形,延长至点,使,作于点,证明,根据全等三角形的性质
得到,继而证明为等腰直角三角形,再由勾股定理解得,最后根据线段的和差解题即可.
【详解】解:当时,如图,延长至点,使,作于点,
中,
在与中,
为等腰直角三角形,
;
当时,如图,
延长至点,使,作于点,
中,
在与中,
为等腰直角三角形,
;
综上所述,的长度为或,
故选:A.
【点睛】本题考查全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理等知识,是重要考点,难度一般,掌握相关知识是解题关键.
13.69
【分析】连接CD,由圆内接四边形的性质得∠BDC+∠BAC=180°,可得∠BDC =180°-42°=138°,再由垂径定理得出,则BD=CD,然后根据等腰三角形的性质即可求出∠BDE的度数.
【详解】解:如图,连接CD,
∵A,B,C,D是⊙O上的四个点,
∴∠BDC+∠BAC=180°,
∵∠BAC=42°,
∴∠BDC =180°-42°=138°,
∵OD⊥BC,
∴,
∴BD=CD,
∴∠BDE=∠BDC=,
故答案为:69.
【点睛】本题考查的是圆内接四边形的性质及垂径定理等知识,掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧是解题的关键.
14./0.8
【分析】本题考查了圆周角定理,解直角三角形,以及勾股定理等知识.掌握圆周角的两个定理:①在同圆或等圆中,同弧或等弧所对的圆周角相等.②半圆(或直径)所对的圆周角是直角;
连接,根据直径所对的圆周角是直角,构建两个直角三角形,再利用等弧所对的圆周角相等得:,最后利用等角的三角函数得出结论.
【详解】解:连接,
∵是的直径,
∴,
在中,,
∴,
∵,
∴.
∴.
∴,
∴.
∴.
∴.
故答案为:
15.31
【分析】根据圆周角定理进行求解即可;
【详解】解:由圆周角定理可知:
故答案为:31.
【点睛】本题主要考查圆周角定理,掌握圆周角定理是解题的关键.
16.80°
【详解】解:连接EM,
∵AB=AC,∠BAM=∠CAM,∴AM⊥BC,
∵AM为⊙O的直径,∴∠ADM=∠AEM=90°,
∴∠AME=∠AMD=90°﹣∠BMD=50°∴∠EAM=40°,
∴∠EOM=2∠EAM=80°,
故答案为80°.
【点睛】本题考查圆周角定理.
17.30
【分析】由弧与弧相等推得弧和弧相等,再根据在同圆中,等弧所对的圆周角相等,从而求出的度数.
【详解】解:∵弧与弧相等,
∴弧和弧相等,
∴;
故答案为:30.
【点睛】本题考查圆心角、弧、弦的关系,熟练掌握等弧所对的圆周角相等是解题的关键.
18.(1)作图见解析;(2)
【分析】(1)根据扇形定义及题目要求画出即可;
(2)根据扇形的面积公式计算即可.
【详解】解:(1)如图所示:
(2),,
,
故.
【点睛】本题考查的是扇形面积的计算,解题的关键是根据题意求出对应圆心角度数是前提,掌握扇形的面积公式.
19.(1)75°;(2)20°
【分析】(1)根据圆心角、弧、弦之间的关系求出∠MON=∠MOC=∠BOC=35°,再求出答案即可;
(2)根据三角形外角性质求出∠AEF,根据圆内接四边形的性质得出∠AEF+∠ABF=180°,求出∠ABF,根据圆周角定理求出∠AFB=90°,再根据三角形内角和定理求出即可.
【详解】解:(1)∵,∠MON=35°,
∴∠MON=∠MOC=∠BOC=35°,
∴∠AON=180°﹣∠MON﹣∠MOC﹣∠BOC=180°﹣35°﹣35°﹣35°=75°;
(2)连接BF,
∵AD⊥直线,
∴∠ADE=90°,
∵∠DAE=20°,
∴∠AEF=∠ADE+∠DAE=110°,
∵四边形为圆内接四边形,
∴∠ABF+∠AEF=180°,
∴∠ABF=70°,
∵AB是⊙O的直径,
∴∠AFB=90°,
∴∠BAF=180°﹣∠AFB﹣∠ABF=20°.
【点睛】本题考查的是圆心角与弧之间的关系,圆的内接四边形的性质,圆周角定理,掌握以上知识是解题的关键.
20.见解析.
【分析】首先延长AO交⊙O于N,连接BN,根据圆周角定理与AD⊥BC,可得∠ABN=∠ADC=90°,又由∠C=∠N,可得∠BAN=∠DAC,然后根据AM平分∠BAC,即可证得∠MAO=∠MAD.
【详解】证明:延长AO交⊙O于N,连接BN,
∵AN是⊙O的直径,AD⊥BC,
∴∠ABN=∠ADC=90°,
∴∠BAN+∠N=90°,∠DAC+∠C=90°,
∵∠N=∠C,
∴∠BAN=∠DAC,
∵AM平分∠BAC, 即∠BAM=∠CAM,
∴∠MAO=∠MAD.
【点睛】本题主要考查了圆周角定理以及角平分线的定义,解题的关键是准确作出辅助线,掌握圆周角定理的应用.
21.(1)见解析
(2)
【分析】(1)根据圆内接四边形的性质得到,根据同角的补角相等证明结论;
(2)根据圆周角定理得到,根据三角形内角和定理计算即可.
【详解】(1)证明:四边形内接于圆,
,
,
;
(2)解:,
,
.
【点睛】本题考查的是圆内接四边形的性质、圆周角定理,解题的关键是掌握圆内接四边形的对角互补.
22.(1)∠A=90°﹣α;(2)∠A=60°.
【分析】(1)根据圆内接四边形的性质得到∠A=∠BCF,再利用三角形外角性质得∠EBF=∠A+∠E,由三角形内角和定理得∠EBF=180°-∠BCF-∠F,所以∠A+∠E=180-∠A-∠F,然后利用∠E+∠F=α可得∠A=90°-α;
(2)利用(1)中的结论进行计算.
【详解】(1)∵四边形ABCD为⊙O的内接四边形,
∴∠A=∠BCF,
∵∠EBF=∠A+∠E,
而∠EBF=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180°﹣∠BCF﹣∠F,
∴∠A+∠E=180﹣∠A﹣∠F,
即2∠A=180°﹣(∠E+∠F),
∵∠E+∠F=α,
∴∠A=90°﹣α;
(2)当α=60°时,∠A=90°﹣×60°=60°.
【点睛】本题考查了圆内接四边形的性质:圆内接四边形的对角互补;圆内接四边形的任意一个外角等于它的内对角.
23.见解析
【分析】根据题意画出示意图,其中BC表示电影幕的宽,G、I分别为圆弧形排列的座位中的任意两个,根据图形可知∠BGC、∠BJC分别为两个座位的视角,由此结合圆周角定理的推论求解即可.
【详解】根据题意画出图形,BC表示电影幕的宽,
由同弧所对圆周角相等可知∠BGC=∠BJC,即同排的观众视角相等.
【点睛】本题是圆周角定理的推论在实际问题中的应用,解题的关键是要理解在同排的观众视角需相同.
24.见解析
【分析】连接AD,由于AB=CD,所以 ,从而得到,再根据同弧所对的圆周角相等得到∠BAD=∠CDA,最后由等角对等边证得DE=AE.
【详解】解:证明:连接AD,
∵AB=CD,
∴ ,
∴,
即 ,
∴∠BAD=∠CDA,
∴DE=AE(等角对等边).
【点睛】本题考查了在同圆中,圆周角、弧、弦的关系及等腰三角形的判定,根据题意作出辅助线,构造出等腰三角形是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
