2.6弧长与扇形面积同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
2.6弧长与扇形面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
A.2cm2 B.4cm2 C.4cm2 D.πcm2
2.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( )
A. B. C.7 D.6
3.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
4.道路施工部门在铺设如图所示的管道时,需要先按照其中心线计算长度后再备料.图中的管道中心线的长为(单位:m)( )
A. B. C. D.
5.在数学跨学科主题活动课上,芳芳用半径,圆心角的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是( )
A. B. C. D.
6.已知扇形的半径为6,圆心角为.则它的面积是( )
A. B. C. D.
7.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
8.圆心角为60°,且半径为12的扇形的面积等于( )
A.48π B.24π C.4π D.2π
9.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地 B.老鼠先到达B地
C.猫和老鼠同时到达B地 D.无法确定
10.如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连接CD,当CD取得最大值时,扇形OAB的面积为( )
A. B. C. D.
11.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.3π B.6π C.5π D.4π
12.如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
A.4π cm B.3π cm C.2π cm D.π cm
二、填空题
13.将等腰直角三角板与量角器按如图所示的方式摆放,使三角板的直角顶点与量角器的中心O重合,且两条直角边分别与量角器边缘所在的弧交于A、B两点.若厘米,则的长度为 厘米.(结果保留)
14.如图,从一块边长为,的菱形铁片上剪出一个扇形,这个扇形在以为圆心的圆上(阴影部分),且圆弧与,分别相切于点,,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是 .
15.如图,正六边形的边长为6,点B,F在上,若图中阴影部分恰是一个圆锥的侧面展开图,则这个圆锥高为 .
16.如图,在的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.、A、分别是小正方形的顶点,则扇形的弧长等于 .(结果保留根号及).
17.已知扇形的弧长为,面积为,则此扇形的圆心角为 度.
三、解答题
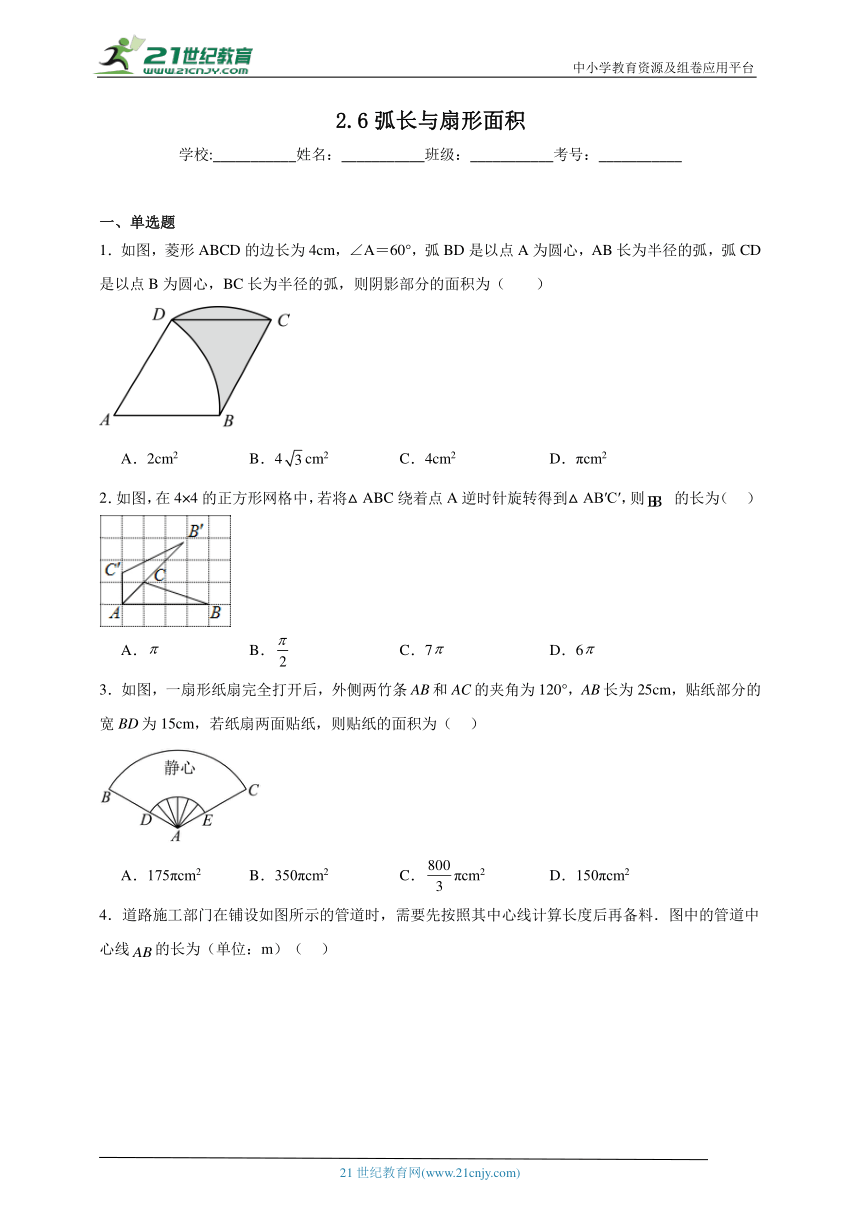
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
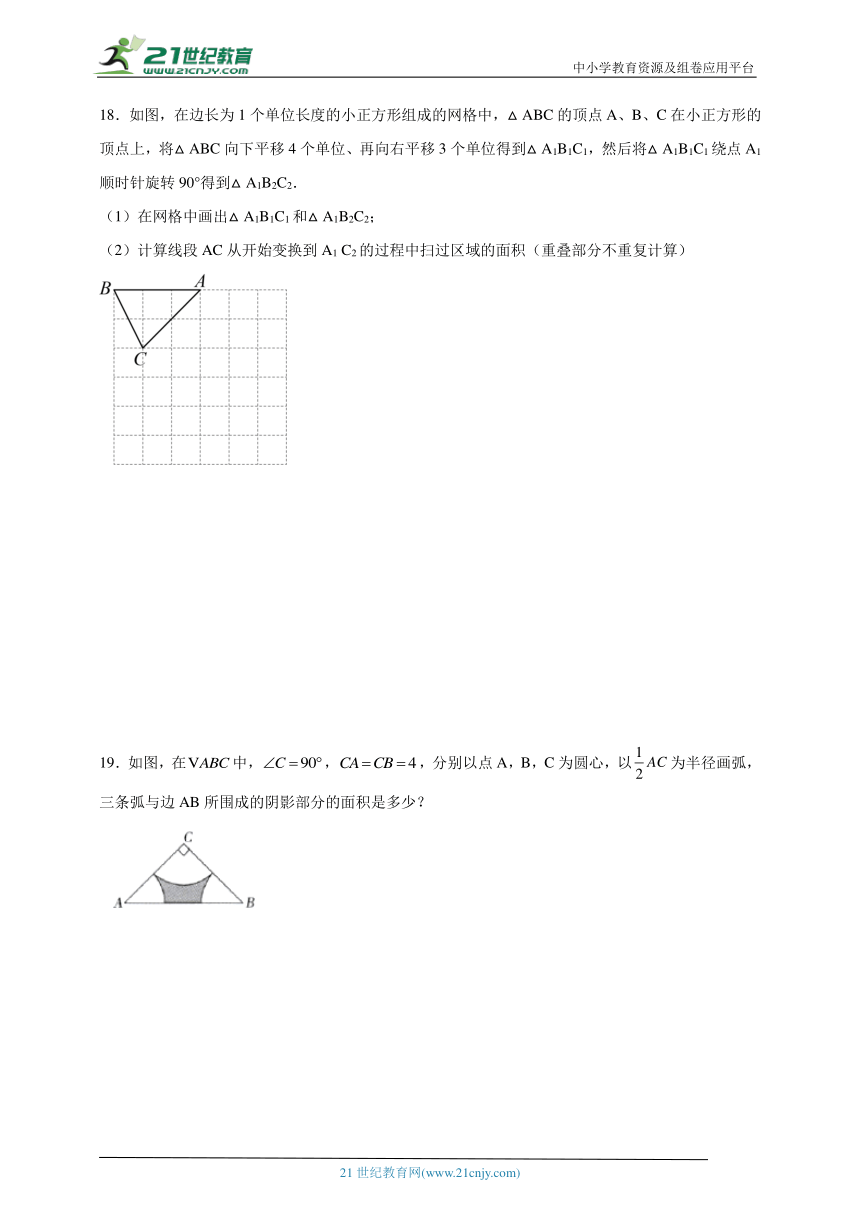
19.如图,在中,,,分别以点A,B,C为圆心,以为半径画弧,三条弧与边AB所围成的阴影部分的面积是多少?
20.如图,是的直径,点是延长线上的一点,点在上,且AC=CD,.
求证:是的切线;
若的半径为,求图中阴影部分的面积.
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当AB=4,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
22.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
23.制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
24.如图,点,将绕点旋转得到.
(1)请在图中画出,并写出点的坐标;
(2)求旋转过程中点的轨迹长.
《2.6弧长与扇形面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B C D C B C A
题号 11 12
答案 B C
1.B
【分析】连接BD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠ABD=60°,再求出∠CBD=60°,DB=BC=AD,从而确定S扇形BDC=S扇形ABD,然后求出阴影部分的面积=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD,计算即可得解.
【详解】解:如图,连接BD,
∵四边形ABCD是菱形,
∴AB=AD=BC,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,AD=DB=BC=4
又∵菱形的对边AD∥BC,
∴∠CBD=∠ADB=60°,
∴S扇形BDC=S扇形ABD
∴S阴影=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD==4cm2.
故选B.
【点睛】本题考查了菱形的性质,等边三角形的性质和面积,熟记性质并作辅助线构造出等边三角形是解题的关键.
2.A
【详解】解:根据图示知,∠BAB′=∠CAC ′=45°,
∴的长为:.
故选A.
3.B
【分析】贴纸部分的面积等于大扇形的面积减去小扇形ADE的面积,由此即可解答.
【详解】∵AB=25,BD=15,
∴AD=10,
∴S贴纸= =175π×2=350cm2,
故选B.
【点睛】本题主要考查扇形面积的计算的应用,解答本题的关键是熟练掌握扇形面积计算公式.
4.B
【分析】根据题意,求长即可求解.
【详解】解:依题意,,
故选:B.
【点睛】本题考查了求弧长,掌握弧长公式是解题的关键.
5.C
【分析】利用扇形的弧长等于圆锥的底圆周长求解即可.
【详解】解:由题意可知:
扇形的弧长
设底面圆半径为r,
∵扇形的弧长等于圆锥的底圆周长
∴,解得:,
故选:C.
【点睛】本题考查弧长公式,解题的关键是理解扇形的弧长等于圆锥的底圆周长.
6.D
【分析】已知扇形的半径和圆心角度数求扇形的面积,选择公式直接计算即可.
【详解】解:.
故选:D
【点睛】本题考查扇形面积公式的知识点,熟知扇形面积公式及适用条件是解题的关键.
7.C
【分析】根据翻折的性质,可得到,进而求出,,再根据进行计算即可.
【详解】解:如图,
由翻折的性质可知,, ,
∵,
∴,
在中,,
∴,
∴,
∴,
∴,
∴
,
故选:C.
【点睛】本题考查扇形面积的计算,掌握扇形面积的计算方法,翻折的性质以及解直角三角形是正确解答的前提.
8.B
【分析】直接根据扇形的面积公式进行计算.
【详解】解:根据扇形的面积公式,得
S==24π(cm2).
故选B.
【点睛】本题主要是考查了扇形的面积公式,掌握扇形的面积公式是解题的关键.
9.C
【详解】解:以AB为直径的半圆的长是: AB.
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:a+b+c+d=(a+b+c+d)= AB.
故猫和老鼠行走的路径长相同.
故选C.
10.A
【分析】∠AOB=90°时,CD最大,由求出扇形面积即可.
【详解】解:解:由PC⊥OA,PD⊥OB可知,∠OCP+∠ODP=180°,
∴O、C、P、D四点共圆,CD为此圆直径时,CD最大,
∴当∠AOB=90°时,CD最大,如图:
此时扇形面积为.
故选:A.
【点睛】本题考查扇形面积计算,解题的关键是掌握∠AOB=90°时,CD最大.
11.B
【详解】阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积.
则阴影部分的面积是:=6π
故选:B.
12.C
【分析】点D所转过的路径长是一段弧,是一段圆心角为180°,半径为OD的弧,故根据弧长公式计算即可.
【详解】解:BD=4,
∴OD=2
∴点D所转过的路径长==2π.
故选:C.
【点睛】本题主要考查了弧长公式:.
13./
【分析】直接根据弧长公式进行计算即可.
【详解】,
,
故答案为:.
【点睛】本题考查了弧长公式,即,熟练掌握知识点是解题的关键.
14.
【分析】先利用菱形的性质得到含30°角的直角三角形,再利用勾股定理求出AE,最后利用弧长公式求出弧长,弧长即为圆锥底面圆的周长,再利用周长公式即可求半径.
【详解】解:如图,连接AE,由切线性质可知:AE⊥BC,即∠AEB=90°;
∵菱形铁片上∠BAD=120°,
∴∠B=180°-120°=60°,
∴∠BAE=30°,
∴AB=2BE=2,
∴BE=1,
∵,
∴,
∴扇形的弧长为:,
所以圆锥底面圆半径为:,
故答案为:.
【点睛】本题考查了菱形的性质、含30°角的直角三角形的性质、勾股定理、弧长公式等内容,解决本题的关键是牢记相关性质与公式,本题需要学生理解扇形与圆锥的关系,蕴含了一定的空间想象思维,涉及到了数形结合等思想方法.
15.
【分析】本题考查了正多边形的内角,圆锥的侧面展开图的弧长与底面圆的关系,母线、底面圆的半径和圆锥的高构成直角三角形的关系,弄清弧长与圆锥的底面圆的周长的关系及母线、底面圆的半径和高的关系是解题的关键.
根据正六边形的内角和,即可求得内角的度数,进而根据边长等于的半径,根据弧长公式求得弧的长,再根据底面圆的周长就是弧的长,求得底面圆的半径,进而根据母线、底面圆的半径和圆锥的高构成直角三角形,求解.
【详解】解:∵正六边形的边长为6,
∴,
∴弧的长为:,
∵图中阴影部分恰是一个圆锥的侧面展开图.
∴弧的长即为圆锥底面的周长,
设圆锥底面圆的半径为,则,
解得:,
∴圆锥的高,
故答案为:.
16.
【分析】根据正方形的性质,得扇形所在的圆心角是,进而求得扇形的半径,即可解题.
【详解】解:根据图形中正方形的性质,得:
,,
∴扇形的弧长为:.
故答案为:.
【点睛】本题主要考查了扇形周长的计算,熟练掌握弧长的计算公式:,是解题的关键.
17.60
【分析】本题考查求扇形的圆心角,根据扇形的面积公式进行求解即可.
【详解】解:设扇形的半径为,圆心角的度数为,
由题意,得:,
∴,
∴,
∴;
故答案为:60.
18.见解析
【详解】试题分析:(1)根据图形平移及旋转的性质画出△A1B1C1及△A1B2C2即可;
(2)根据图形平移及旋转的性质可知,将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以以2为半径,圆心角为90°的扇形的面积,再减去重叠部分的面积,根据平行四边形的面积及扇形面积公式进行解答即可.
解:(1)如图所示:
(2)∵图中是边长为1个单位长度的小正方形组成的网格,
∴AC==2,
∵将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以2为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2为半径,圆心角为45°的扇形的面积,
∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+﹣=14+π.
点评:本题考查的是旋转变换及平移变换,扇形的面积公式,熟知图形旋转、平移不变性的特点是解答此题的关键.
19.
【分析】由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出S△ABC=×4×4=8,然后代入即可得到答案.
【详解】∵∠C=90°,CA=CB=4,
∴AC=2,S△ABC=×4×4=8,
∵三条弧所对的圆心角的和为180°,
三个扇形的面积和=×π×22=2π,
∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=8-2π.
故答案为8-2π.
【点睛】本题考查了等腰直角三角形的性质,得出阴影部分的面积=S△ABC-三个扇形的面积和是解题关键.
20.(1)见解析;(2)
【分析】(1)根据圆周角定理和等腰三角形的性质,即可得到答案;
(2)根据扇形面积公式进行计算,即可得到答案.
【详解】证明:连接.
,
.
,
.
.即,
是的切线.
解:,
.
,
在中,,
,
,
图中阴影部分的面积.
【点睛】本题考查圆周角定理、等腰三角形的性质和扇形面积公式,解题的关键是掌握圆周角定理、等腰三角形的性质和扇形面积公式
21.(1)详见解析;(2)4.
【分析】(1)连接OD,利用三角形中位线的性质可以得到OD∥BC,然后根据DE⊥BC即可得到OD⊥DE,从而判断DE是圆的切线;
(2)过点O作OF⊥AD,垂足为F,根据平行线的性质得出∠ADO的度数,然后根据等腰三角形的性质和勾股定理得到∠AOD的度数和AD,OF的长度,然后利用扇形面积减去三角形面积即可求得阴影部分面积.
【详解】解:(1)连接OD,
∵AB是⊙O的直径,D是AC的中点,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∵点D在圆上,
∴DE为⊙O的切线;
(2)过点O作OF⊥AD,垂足为F,
∵OD∥BC,
∴∠ADO=∠C =30°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∴∠A=∠C,∠AOD=120°,
∴AB=BC=4,
∵OD是△ABC的中位线,
∴OD=2, OF=,
∴AF= =3,
∴AD=2AF=6,
∴S△AOD=AD OF=×6×=3,
∴阴影部分面积S=﹣3=.
【点睛】本题主要考查切线的判定,等腰三角形的判定及性质,三角形内角和定理及扇形的面积公式,能够作出辅助线是解题的关键.
22.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【分析】(1)设它的侧面展开图的圆心角为n°,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,然后求出n的值即可;
(2)连接BB′,如图,根据两点之间线段对短得到BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,然后利用△ABB′为等腰直角三角形得到BB′的长.
【详解】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
【点睛】本题考查了求圆锥侧面展开图的圆心角和在圆锥侧面求最短路径问题,解答关键是根据公式计算求出圆心角和将立体问题转化为平面问题加以解决.
23.(3000+1000π)mm
【详解】试题分析:先求出两个弯形管道的弧长,然后再加上直管部分即可.
试题解析:,
中心虚线的长度为
(mm).
24.(1)图形见解析, ;(2)5π.
【分析】(1)根据关于原点对称的点的坐标特点画出△A′B′C′,并写出点A′的坐标即可;
(2)连接OA,先根据勾股定理求出OA的长,再根据弧长公式即可得出结论.
【详解】解:(1)如图所示,即为所求出;;
(2)连接,
∵,
∴旋转过程中点的轨迹长.
【点睛】本题考查的是作图变换 旋转,熟知图形旋转不变性的性质是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.6弧长与扇形面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,菱形ABCD的边长为4cm,∠A=60°,弧BD是以点A为圆心,AB长为半径的弧,弧CD是以点B为圆心,BC长为半径的弧,则阴影部分的面积为( )
A.2cm2 B.4cm2 C.4cm2 D.πcm2
2.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则的长为( )
A. B. C.7 D.6
3.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为( )
A.175πcm2 B.350πcm2 C.πcm2 D.150πcm2
4.道路施工部门在铺设如图所示的管道时,需要先按照其中心线计算长度后再备料.图中的管道中心线的长为(单位:m)( )
A. B. C. D.
5.在数学跨学科主题活动课上,芳芳用半径,圆心角的扇形纸板,做了一个圆锥形的生日帽,如图所示.在不考虑接缝的情况下,这个圆锥形生日帽的底面圆半径是( )
A. B. C. D.
6.已知扇形的半径为6,圆心角为.则它的面积是( )
A. B. C. D.
7.如图.将扇形翻折,使点A与圆心O重合,展开后折痕所在直线l与交于点C,连接.若,则图中阴影部分的面积是( )
A. B. C. D.
8.圆心角为60°,且半径为12的扇形的面积等于( )
A.48π B.24π C.4π D.2π
9.如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是( )
A.猫先到达B地 B.老鼠先到达B地
C.猫和老鼠同时到达B地 D.无法确定
10.如图,已知扇形OAB的半径OA=6,点P为弧AB上一动点,过点P作PC⊥OA,PD⊥OB,连接CD,当CD取得最大值时,扇形OAB的面积为( )
A. B. C. D.
11.如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.3π B.6π C.5π D.4π
12.如图,已知□ABCD的对角线BD=4cm,将□ABCD绕其对称中心O旋转180°,则点D所转过的路径长为( )
A.4π cm B.3π cm C.2π cm D.π cm
二、填空题
13.将等腰直角三角板与量角器按如图所示的方式摆放,使三角板的直角顶点与量角器的中心O重合,且两条直角边分别与量角器边缘所在的弧交于A、B两点.若厘米,则的长度为 厘米.(结果保留)
14.如图,从一块边长为,的菱形铁片上剪出一个扇形,这个扇形在以为圆心的圆上(阴影部分),且圆弧与,分别相切于点,,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径是 .
15.如图,正六边形的边长为6,点B,F在上,若图中阴影部分恰是一个圆锥的侧面展开图,则这个圆锥高为 .
16.如图,在的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.、A、分别是小正方形的顶点,则扇形的弧长等于 .(结果保留根号及).
17.已知扇形的弧长为,面积为,则此扇形的圆心角为 度.
三、解答题
18.如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1,然后将△A1B1C1绕点A1顺时针旋转90°得到△A1B2C2.
(1)在网格中画出△A1B1C1和△A1B2C2;
(2)计算线段AC从开始变换到A1 C2的过程中扫过区域的面积(重叠部分不重复计算)
19.如图,在中,,,分别以点A,B,C为圆心,以为半径画弧,三条弧与边AB所围成的阴影部分的面积是多少?
20.如图,是的直径,点是延长线上的一点,点在上,且AC=CD,.
求证:是的切线;
若的半径为,求图中阴影部分的面积.
21.如图,以AB为直径的⊙O经过AC的中点D,DE⊥BC于点E.
(1)求证:DE是⊙O的切线;
(2)当AB=4,∠C=30°时,求图中阴影部分的面积(结果保留根号和π).
22.如图,圆锥母线的长l等于底面半径r的4倍,
(1)求它的侧面展开图的圆心角.
(2)当圆锥的底面半径r=4cm时,求从B点出发沿圆锥侧面绕一圈回到B点的最短路径的长
23.制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB的长为3 000mm,弯形管道部分BC,CD弧的半径都是1 000mm,∠O=∠O’=90°,计算图中中心虚线的长度.
24.如图,点,将绕点旋转得到.
(1)请在图中画出,并写出点的坐标;
(2)求旋转过程中点的轨迹长.
《2.6弧长与扇形面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A B B C D C B C A
题号 11 12
答案 B C
1.B
【分析】连接BD,判断出△ABD是等边三角形,根据等边三角形的性质可得∠ABD=60°,再求出∠CBD=60°,DB=BC=AD,从而确定S扇形BDC=S扇形ABD,然后求出阴影部分的面积=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD,计算即可得解.
【详解】解:如图,连接BD,
∵四边形ABCD是菱形,
∴AB=AD=BC,
∵∠A=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,AD=DB=BC=4
又∵菱形的对边AD∥BC,
∴∠CBD=∠ADB=60°,
∴S扇形BDC=S扇形ABD
∴S阴影=S扇形BDC-(S扇形ABD-S△ABD)=S△ABD==4cm2.
故选B.
【点睛】本题考查了菱形的性质,等边三角形的性质和面积,熟记性质并作辅助线构造出等边三角形是解题的关键.
2.A
【详解】解:根据图示知,∠BAB′=∠CAC ′=45°,
∴的长为:.
故选A.
3.B
【分析】贴纸部分的面积等于大扇形的面积减去小扇形ADE的面积,由此即可解答.
【详解】∵AB=25,BD=15,
∴AD=10,
∴S贴纸= =175π×2=350cm2,
故选B.
【点睛】本题主要考查扇形面积的计算的应用,解答本题的关键是熟练掌握扇形面积计算公式.
4.B
【分析】根据题意,求长即可求解.
【详解】解:依题意,,
故选:B.
【点睛】本题考查了求弧长,掌握弧长公式是解题的关键.
5.C
【分析】利用扇形的弧长等于圆锥的底圆周长求解即可.
【详解】解:由题意可知:
扇形的弧长
设底面圆半径为r,
∵扇形的弧长等于圆锥的底圆周长
∴,解得:,
故选:C.
【点睛】本题考查弧长公式,解题的关键是理解扇形的弧长等于圆锥的底圆周长.
6.D
【分析】已知扇形的半径和圆心角度数求扇形的面积,选择公式直接计算即可.
【详解】解:.
故选:D
【点睛】本题考查扇形面积公式的知识点,熟知扇形面积公式及适用条件是解题的关键.
7.C
【分析】根据翻折的性质,可得到,进而求出,,再根据进行计算即可.
【详解】解:如图,
由翻折的性质可知,, ,
∵,
∴,
在中,,
∴,
∴,
∴,
∴,
∴
,
故选:C.
【点睛】本题考查扇形面积的计算,掌握扇形面积的计算方法,翻折的性质以及解直角三角形是正确解答的前提.
8.B
【分析】直接根据扇形的面积公式进行计算.
【详解】解:根据扇形的面积公式,得
S==24π(cm2).
故选B.
【点睛】本题主要是考查了扇形的面积公式,掌握扇形的面积公式是解题的关键.
9.C
【详解】解:以AB为直径的半圆的长是: AB.
设四个小半圆的直径分别是a,b,c,d,则a+b+c+d=AB.
则老鼠行走的路径长是:a+b+c+d=(a+b+c+d)= AB.
故猫和老鼠行走的路径长相同.
故选C.
10.A
【分析】∠AOB=90°时,CD最大,由求出扇形面积即可.
【详解】解:解:由PC⊥OA,PD⊥OB可知,∠OCP+∠ODP=180°,
∴O、C、P、D四点共圆,CD为此圆直径时,CD最大,
∴当∠AOB=90°时,CD最大,如图:
此时扇形面积为.
故选:A.
【点睛】本题考查扇形面积计算,解题的关键是掌握∠AOB=90°时,CD最大.
11.B
【详解】阴影部分的面积=以AB′为直径的半圆的面积+扇形ABB′的面积-以AB为直径的半圆的面积.
则阴影部分的面积是:=6π
故选:B.
12.C
【分析】点D所转过的路径长是一段弧,是一段圆心角为180°,半径为OD的弧,故根据弧长公式计算即可.
【详解】解:BD=4,
∴OD=2
∴点D所转过的路径长==2π.
故选:C.
【点睛】本题主要考查了弧长公式:.
13./
【分析】直接根据弧长公式进行计算即可.
【详解】,
,
故答案为:.
【点睛】本题考查了弧长公式,即,熟练掌握知识点是解题的关键.
14.
【分析】先利用菱形的性质得到含30°角的直角三角形,再利用勾股定理求出AE,最后利用弧长公式求出弧长,弧长即为圆锥底面圆的周长,再利用周长公式即可求半径.
【详解】解:如图,连接AE,由切线性质可知:AE⊥BC,即∠AEB=90°;
∵菱形铁片上∠BAD=120°,
∴∠B=180°-120°=60°,
∴∠BAE=30°,
∴AB=2BE=2,
∴BE=1,
∵,
∴,
∴扇形的弧长为:,
所以圆锥底面圆半径为:,
故答案为:.
【点睛】本题考查了菱形的性质、含30°角的直角三角形的性质、勾股定理、弧长公式等内容,解决本题的关键是牢记相关性质与公式,本题需要学生理解扇形与圆锥的关系,蕴含了一定的空间想象思维,涉及到了数形结合等思想方法.
15.
【分析】本题考查了正多边形的内角,圆锥的侧面展开图的弧长与底面圆的关系,母线、底面圆的半径和圆锥的高构成直角三角形的关系,弄清弧长与圆锥的底面圆的周长的关系及母线、底面圆的半径和高的关系是解题的关键.
根据正六边形的内角和,即可求得内角的度数,进而根据边长等于的半径,根据弧长公式求得弧的长,再根据底面圆的周长就是弧的长,求得底面圆的半径,进而根据母线、底面圆的半径和圆锥的高构成直角三角形,求解.
【详解】解:∵正六边形的边长为6,
∴,
∴弧的长为:,
∵图中阴影部分恰是一个圆锥的侧面展开图.
∴弧的长即为圆锥底面的周长,
设圆锥底面圆的半径为,则,
解得:,
∴圆锥的高,
故答案为:.
16.
【分析】根据正方形的性质,得扇形所在的圆心角是,进而求得扇形的半径,即可解题.
【详解】解:根据图形中正方形的性质,得:
,,
∴扇形的弧长为:.
故答案为:.
【点睛】本题主要考查了扇形周长的计算,熟练掌握弧长的计算公式:,是解题的关键.
17.60
【分析】本题考查求扇形的圆心角,根据扇形的面积公式进行求解即可.
【详解】解:设扇形的半径为,圆心角的度数为,
由题意,得:,
∴,
∴,
∴;
故答案为:60.
18.见解析
【详解】试题分析:(1)根据图形平移及旋转的性质画出△A1B1C1及△A1B2C2即可;
(2)根据图形平移及旋转的性质可知,将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以以2为半径,圆心角为90°的扇形的面积,再减去重叠部分的面积,根据平行四边形的面积及扇形面积公式进行解答即可.
解:(1)如图所示:
(2)∵图中是边长为1个单位长度的小正方形组成的网格,
∴AC==2,
∵将△ABC向下平移4个单位AC所扫过的面积是以4为底,以2为高的平行四边形的面积;再向右平移3个单位AC扫过的面积是以3为底以2为高的平行四边形的面积;当△A1B1C1绕点A1顺时针旋转90°到△A1B2C2时,A1C1所扫过的面积是以A1为圆心以2为半径,圆心角为90°的扇形的面积,重叠部分是以A1为圆心,以2为半径,圆心角为45°的扇形的面积,
∴线段AC在变换到A1C2的过程中扫过区域的面积=4×2+3×2+﹣=14+π.
点评:本题考查的是旋转变换及平移变换,扇形的面积公式,熟知图形旋转、平移不变性的特点是解答此题的关键.
19.
【分析】由于三条弧所对的圆心角的和为180°,根据扇形的面积公式可计算出三个扇形的面积和,而三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和,再利用三角形的面积公式计算出S△ABC=×4×4=8,然后代入即可得到答案.
【详解】∵∠C=90°,CA=CB=4,
∴AC=2,S△ABC=×4×4=8,
∵三条弧所对的圆心角的和为180°,
三个扇形的面积和=×π×22=2π,
∴三条弧与边AB所围成的阴影部分的面积=S△ABC-三个扇形的面积和=8-2π.
故答案为8-2π.
【点睛】本题考查了等腰直角三角形的性质,得出阴影部分的面积=S△ABC-三个扇形的面积和是解题关键.
20.(1)见解析;(2)
【分析】(1)根据圆周角定理和等腰三角形的性质,即可得到答案;
(2)根据扇形面积公式进行计算,即可得到答案.
【详解】证明:连接.
,
.
,
.
.即,
是的切线.
解:,
.
,
在中,,
,
,
图中阴影部分的面积.
【点睛】本题考查圆周角定理、等腰三角形的性质和扇形面积公式,解题的关键是掌握圆周角定理、等腰三角形的性质和扇形面积公式
21.(1)详见解析;(2)4.
【分析】(1)连接OD,利用三角形中位线的性质可以得到OD∥BC,然后根据DE⊥BC即可得到OD⊥DE,从而判断DE是圆的切线;
(2)过点O作OF⊥AD,垂足为F,根据平行线的性质得出∠ADO的度数,然后根据等腰三角形的性质和勾股定理得到∠AOD的度数和AD,OF的长度,然后利用扇形面积减去三角形面积即可求得阴影部分面积.
【详解】解:(1)连接OD,
∵AB是⊙O的直径,D是AC的中点,
∴OD是△ABC的中位线,
∴OD∥BC,
∵DE⊥BC,
∴OD⊥DE,
∵点D在圆上,
∴DE为⊙O的切线;
(2)过点O作OF⊥AD,垂足为F,
∵OD∥BC,
∴∠ADO=∠C =30°,
∵OD=OA,
∴∠OAD=∠ODA=30°,
∴∠A=∠C,∠AOD=120°,
∴AB=BC=4,
∵OD是△ABC的中位线,
∴OD=2, OF=,
∴AF= =3,
∴AD=2AF=6,
∴S△AOD=AD OF=×6×=3,
∴阴影部分面积S=﹣3=.
【点睛】本题主要考查切线的判定,等腰三角形的判定及性质,三角形内角和定理及扇形的面积公式,能够作出辅助线是解题的关键.
22.(1)它的侧面展开图的圆心角为90°;(2)BB′=8.
【分析】(1)设它的侧面展开图的圆心角为n°,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和弧长公式得到2πr=,然后求出n的值即可;
(2)连接BB′,如图,根据两点之间线段对短得到BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,然后利用△ABB′为等腰直角三角形得到BB′的长.
【详解】解:(1)设它的侧面展开图的圆心角为n°,
根据题意得2πr=,
而l=2r,
所以2πr=,解得n=90,
所以它的侧面展开图的圆心角为90°;
(2)连接BB′,如图,
此时BB′为从B点出发沿圆锥侧面绕一圈回到B点的最短路径,
∵r=4,
∴l=2r=8,
∵∠BAB′=90°,
∴△ABB′为等腰直角三角形,
∴BB′=AB=8.
【点睛】本题考查了求圆锥侧面展开图的圆心角和在圆锥侧面求最短路径问题,解答关键是根据公式计算求出圆心角和将立体问题转化为平面问题加以解决.
23.(3000+1000π)mm
【详解】试题分析:先求出两个弯形管道的弧长,然后再加上直管部分即可.
试题解析:,
中心虚线的长度为
(mm).
24.(1)图形见解析, ;(2)5π.
【分析】(1)根据关于原点对称的点的坐标特点画出△A′B′C′,并写出点A′的坐标即可;
(2)连接OA,先根据勾股定理求出OA的长,再根据弧长公式即可得出结论.
【详解】解:(1)如图所示,即为所求出;;
(2)连接,
∵,
∴旋转过程中点的轨迹长.
【点睛】本题考查的是作图变换 旋转,熟知图形旋转不变性的性质是解答此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
