9.9利用位似放缩图形同步练习(含解析)
文档属性
| 名称 | 9.9利用位似放缩图形同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 15:40:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
9.9利用位似放缩图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知△ABC,任取一点O,连结AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法错误的是( )
A.△ABC与△DEF是位似图形 B.△ABC与△DEF是相似图形
C.△ABC与△DEF的面积之比为4:1 D.△ABC与△DEF的周长之比为4:1
2.在平面直角坐标系中,已知点,,以原点O为位似中心把缩小到原来的则点B的对应点的坐标是( )
A. B.或 C. D.或
3.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若AA':OA'=2:3,则下列说法错误的是( )
A.△A'OB'∽△AOB
B.A'B'//AB
C.点O到A'B'与AB的距离之比为3:5
D.△A'B'C'与△ABC的面积之比为3:5
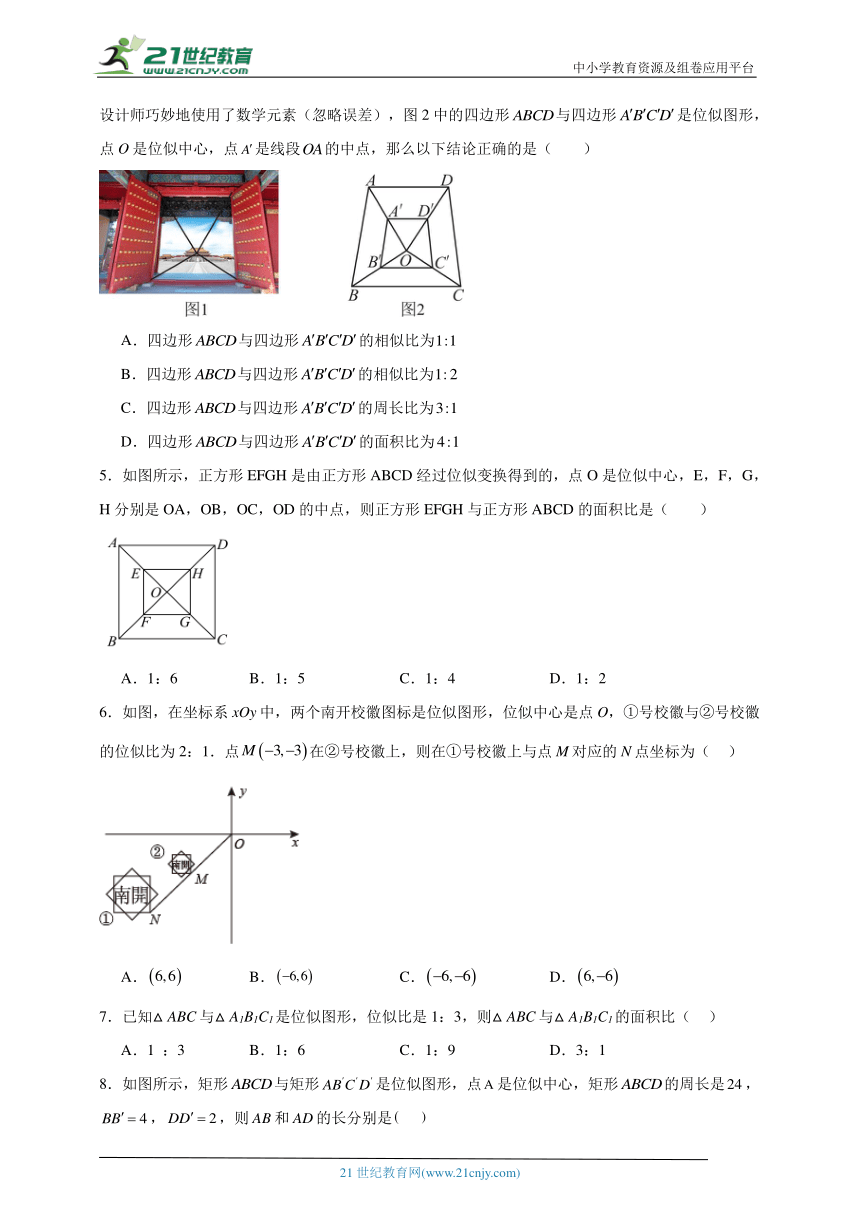
4.2020年是紫禁城建成600年暨故宫博物院成立95周年,在此之前有多个国家曾发行过紫禁城元素的邮品.图1所示的摩纳哥发行的小型张中的图案,以敞开的紫禁城大门和大门内的石狮和太和殿作为邮票和小型张的边饰,如果标记出图1中大门的门框并画出相关的几何图形(图2),我们发现设计师巧妙地使用了数学元素(忽略误差),图2中的四边形与四边形是位似图形,点O是位似中心,点是线段的中点,那么以下结论正确的是( )
A.四边形与四边形的相似比为
B.四边形与四边形的相似比为
C.四边形与四边形的周长比为
D.四边形与四边形的面积比为
5.如图所示,正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E,F,G,H分别是OA,OB,OC,OD的中点,则正方形EFGH与正方形ABCD的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
6.如图,在坐标系xOy中,两个南开校徽图标是位似图形,位似中心是点O,①号校徽与②号校徽的位似比为2:1.点在②号校徽上,则在①号校徽上与点M对应的N点坐标为( )
A. B. C. D.
7.已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )
A.1 :3 B.1:6 C.1:9 D.3:1
8.如图所示,矩形与矩形是位似图形,点是位似中心,矩形的周长是,,,则和的长分别是
A., B., C., D.,
9.如图,与是位似图形,点O为位似中心,若,则与周长比是( )
A. B. C. D.
10. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,
OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是【 】
A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
11.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.无限小数是无理数
C.阴天会下雨是必然事件
D.在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k
12.如图,网格中每个小正方形的边长都是1,的三个顶点均在格点上,与位似,点为位似中心,且位似比为1:2.若在网格中建立坐标系,点的坐标为,则点的对应点的坐标为( )
A. B.或 C. D.或
二、填空题
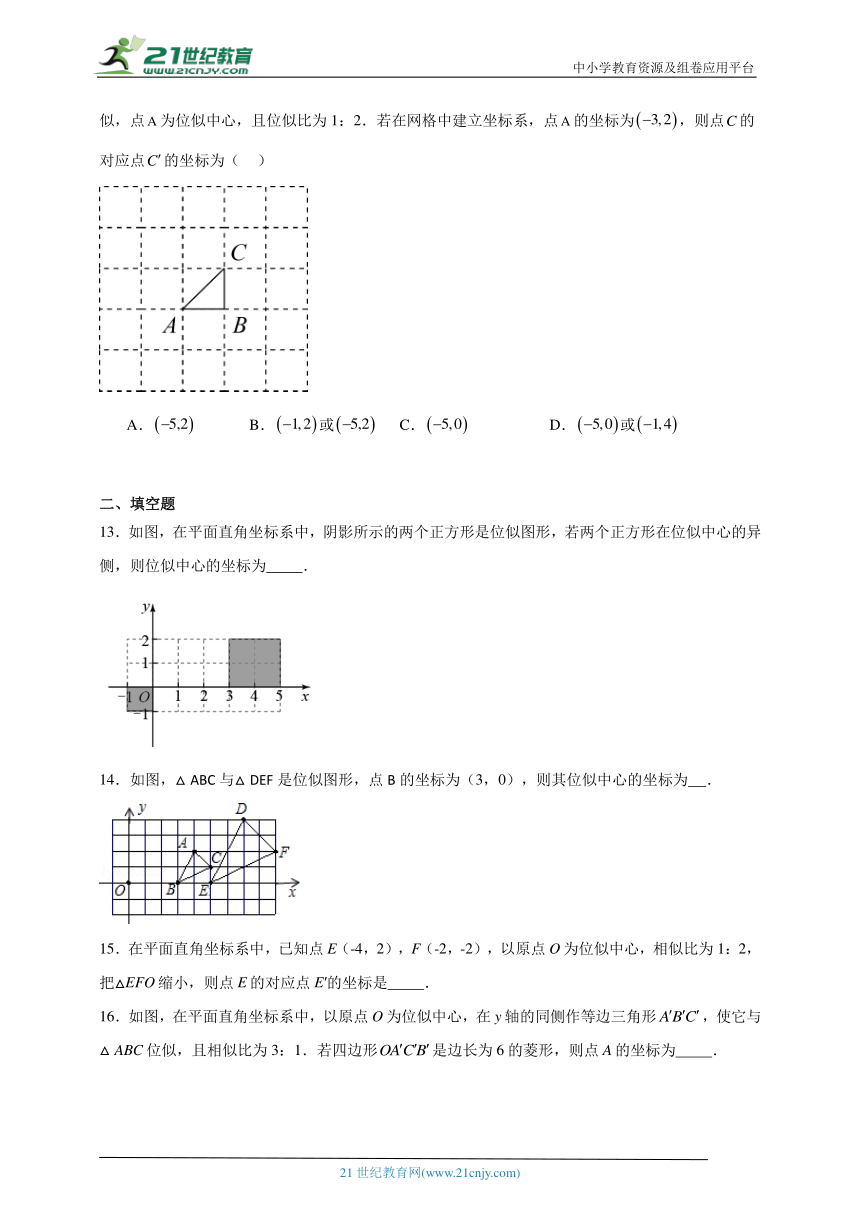
13.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若两个正方形在位似中心的异侧,则位似中心的坐标为 .
14.如图,△ABC与△DEF是位似图形,点B的坐标为(3,0),则其位似中心的坐标为 .
15.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为1:2,把△EFO缩小,则点E的对应点E′的坐标是 .
16.如图,在平面直角坐标系中,以原点O为位似中心,在y轴的同侧作等边三角形,使它与△ABC位似,且相似比为3:1.若四边形是边长为6的菱形,则点A的坐标为 .
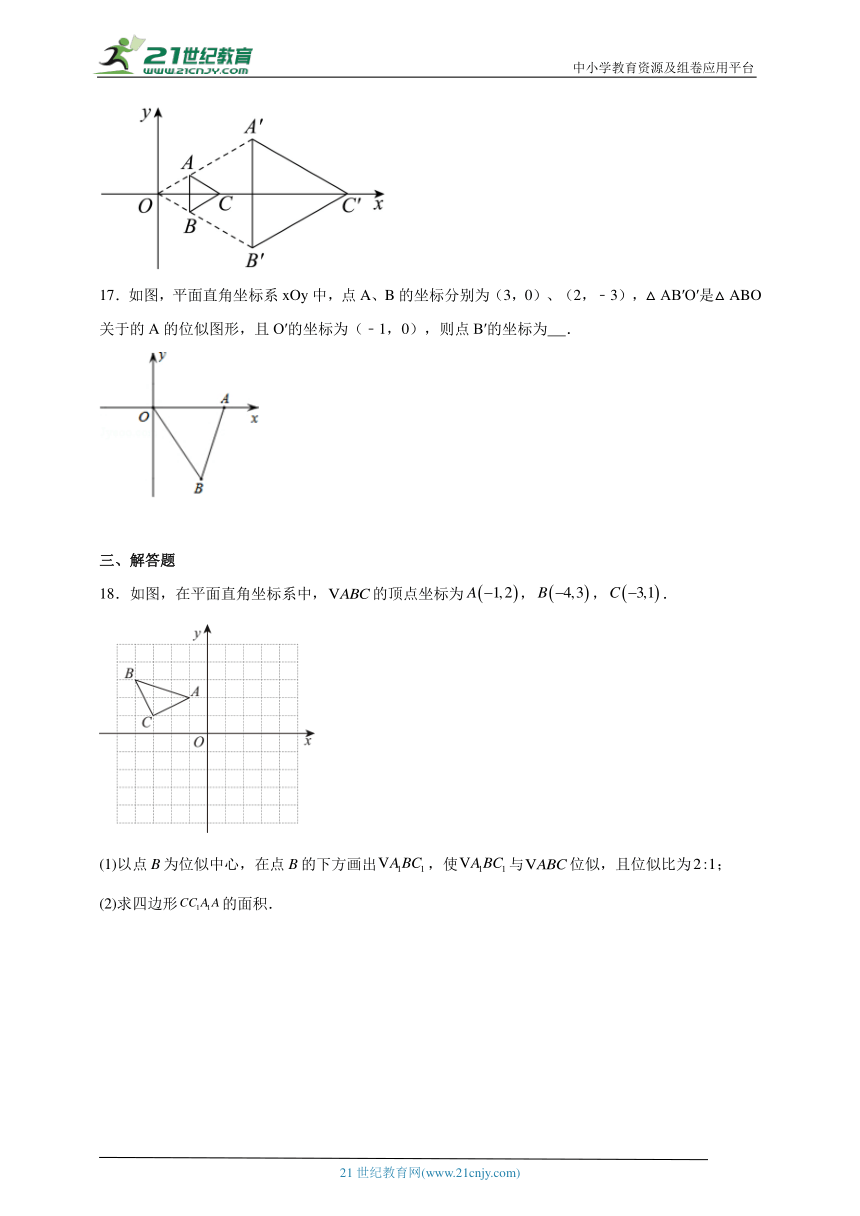
17.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 .
三、解答题
18.如图,在平面直角坐标系中,的顶点坐标为,,.
(1)以点B为位似中心,在点B的下方画出,使与位似,且位似比为;
(2)求四边形的面积.
19.如图在由边长为1个单位长度的小正方形组成的12×12网格中,已知点A,B,C,D均为网格线的交点
(1)在网格中将△ABC绕点D顺时针旋转90°画出旋转后的图形△A1B1C1;
(2)在网格中将△ABC放大2倍得到△DEF,使A与D为对应点.
20.如图,已知五边形A'B'C'D'E'是五边形的位似图形,但被小玮擦去了一部分,你能将它补完整吗?
21.如图,在6×6的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上.按要求完成下列画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以BO为边,画出△OBC,使△OBC∽△ABO,C为格点.
(2)在图2中,以点O为位似中心,在网格内画出△ODE,使△ODE与△OAB位似,且位似比k=2,点D、E为格点.
(3)在图3中,在OA边上找一个点F,且满足.
22.如图,在边长为1的小正方形组成的网格中,的顶点在格点(网格线的交点)上,以点O为原点建立平面直角坐标系,点B的坐标为.
(1)将向左平移5个单位长度,得到,画出;
(2)以点O为位似中心,将放大到两倍(即新图与原图的相似比为2),得到,在所给的方格纸中画出;
(3)若点M是的中点,经过(1)、(2)两次变换,M的对应点M2的坐标是 .
23.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
24.已知点O在内,以点O为位似中心画一个三角形,使它与位似,且相似比为.
《9.9利用位似放缩图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D D C C C B A D
题号 11 12
答案 D D
1.D
【分析】根据位似图形的性质,得出△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
【详解】解:根据位似性质可得:A、△ABC与△DEF是位似图形,故本选项正确,不符合题意;
△ABC与△DEF是相似图形,故B选项正确,不符合题意;
∵将△ABC的三边缩小到原来的,
∴△ABC与△DEF的周长之比为2:1,故D选项不正确,符合题意;
∵面积比等于相似比的平方,
∴△ABC与△DEF的面积之比为4:1,故C选项正确,不符合题意;
故选:D.
【点睛】本题主要考查了位似图形的性质,正确的记忆位似图形性质是解决问题的关键.
2.D
【分析】本题主要考查了位似变换.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或.
根据位似变换的性质,把的横纵坐标乘以或,计算即可.
【详解】∵以原点O为位似中心,相似比为,把缩小,点B的坐标为,
∴点B的对应点的坐标为或,
即或.
故选:D.
3.D
【分析】根据位移变换的性质得到,进而求得,根据相似三角形的性质得到,根据相似三角形的面积比等于相似比的平方解答即可.
【详解】△A'B'C'是△ABC以点O为位似中心经过位似变换得到的
AA':OA'=2:3
即点O到A'B'与AB的距离之比为3:5
所以,选项D错误,
故选:D.
【点睛】本题考查的是位似变换的概念、相似三角形的性质,掌握位似与相似的关系、相似三角形的面积比等于相似比的平方是解题的关键.
4.D
【分析】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.两个位似图形必须是相似形;对应点的连线都经过同一点,对应边平行或共线.先利用位似的性质得到,然后根据相似的性质进行判断.
【详解】解:四边形与四边形是位似图形,点是位似中心,点是线段的中点,
,
∴,
四边形与四边形的相似比为,周长的比为,面积比为.
故选:D.
5.C
【分析】由正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E,F,G,H分别是OA,OB,OC,OD的中点,易求得位似比等于EH:AD=1:2,又由相似三角形面积的比等于相似比的平方,即可求得正方形EFGH与正方形ABCD的面积比.
【详解】∵正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,
∴正方形EFGH∽正方形ABCD,
∵E,F,G,H分别是OA,OB,OC,OD的中点,
∴EH=AD,
即位似比为:EH:AD=1:2,
∴正方形EFGH与正方形ABCD的面积比是:1:4.
故选C.
【点睛】此题考查位似变换,解题关键在于利用相似的性质进行解答.
6.C
【分析】根据两个图形上对应点的横坐标与横坐标之比等于位似比,纵坐标与纵坐标之比等于位似比求解即可.
【详解】解:∵①号校徽与②号校徽的位似比为2:1.点M( 3, 3)在②号校徽上,
∴在①号校徽上与点M对应的N点坐标为(-6,-6),
故选C.
【点睛】本题主要考查了求位似图形对应点的坐标,熟知两个位似图形上对应点的横坐标与横坐标之比等于位似比,纵坐标与纵坐标之比等于位似比是关键.
7.C
【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.
【详解】∵△ABC与△A1B1C1是位似图形,位似比是1:3,
∴△ABC与△A1B1C1的面积比为1:9,
故选:C.
【点睛】本题主要考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.
8.B
【分析】根据矩形的性质得到,根据位似变换的性质得到,根据平行线分线段成比例定理列出比例式,代入计算得到答案.
【详解】解:∵矩形ABCD的周长是24,
∴,
∴,
∵,,
∴,
∵矩形ABCD与矩形是位似图形,
∴,
∴,,
∴,即,
解得,,
则,
故选:B.
【点睛】本题考查了位似图形的性质,熟练掌握位似图形的任意一对对应点与位似中心在同一直线上,它们到位似中心的距离之比等于相似比是解答本题的关键.也考查了平行线分线段成比例定理.
9.A
【分析】根据位似图形是相似图形,相似三角形的周长比等于相似比,进行求解即可.
【详解】解:∵与是位似图形,
∴,
∵,
∴相似比为:,
∴与周长比等于相似比;
故选A.
【点睛】本题考查相似三角形的性质.熟练掌握位似图形是相似图形,相似三角形的周长比等于相似比,是解题的关键.
10.D
【详解】如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一
条直线上,那么这两个图形叫做位似图形.把一个图形变换成与之位似的图形是位似变换.因此,
∵矩形OA′B′C′与矩形OABC关于点O位似,∴矩形OA′B′C′∽矩形OABC.
∵矩形OA′B′C′的面积等于矩形OABC面积的,∴位似比为:.
∵点B的坐标为(-4,6),∴点B′的坐标是:(-2,3)或(2,-3).故选D.
11.D
【分析】根据圆周角定理以及无理数的定义和随机事件的定义和位似图形的性质分别判断得出答案即可.
【详解】解: A、根据必须是同圆或等圆中,相等的圆心角所对的弧才相等,故此选项错误;
B、无限不循环小数是无理数,无限循环小数是有理数,故此选项错误;
C、阴天会下雨是随机事件,故此选项错误;
D、根据位似图形的性质得出:在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k,故此选项正确.
故选:D.
12.D
【分析】根据位似变换的概念和性质、结合图形解答.
【详解】解:如图,
由图可知,点C的坐标为(-2,3),
以点A为位似中心,在网格中画,使与△ABC位似,且位似比为1:2,
则点的坐标为(-5,0)或(-1,4),
故选:D.
【点睛】本题考查位似变换的应用,熟练掌握位似变换的概念和性质是解题关键.
13.
【分析】连接各组对应点,它们在两个正方形之间相交于点,则点为位似中心,然后写出点坐标即可.
【详解】解:如图,点为位似中心,.
故答案为:.
【点睛】本题考查位似变换:位似的两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),掌握位似变换的性质是解题的关键.
14.(1,0)
【详解】分析:利用△ABC与△DEF是位似图形,连接图上对应三点的坐标,连线的交点就是位似中心.
详解:
连接各对应点A,D,与C,F,交点Q即是位似中心的坐标,
∴其位似中心的坐标为:(1,0),
故答案为(1,0).
点睛:本题考查了位似图形的位似中心的确定方法.顺次连接各对应点得出位似中心是解决问题的关键.
15.(-2,1)或(2,-1).
【分析】根据已知得出位似图形对应坐标与位似图形比的关系进而得出答案.
【详解】解:∵顶点E的坐标是(-4,2),以原点O为位似中心相似比为1:2将△EFO缩小得到它的位似图形△E′F′O,
∴点E′的坐标是:(×(-4),×2),[- ×(-4),- ×2],
即(-2,1)或(2,-1).
故答案为(-2,1)或(2,-1).
【点睛】本题考查位似图形的性质,根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k得出是解题的关键.
16.
【分析】根据菱形的性质、等边三角形的性质求出,通过相似比即可得A的坐标.
【详解】解:若四边形是边长为6的菱形,.
∵是等边三角形
∴
则
∵,且相似比为3:1
∴
故答案为:
【点睛】本题主要考查菱形的性质、等边三角形的性质、位似图形的性质,掌握相关知识并灵活应用是解题的关键.
17..
【分析】根据位似图形的性质画出图形,利用对应边之间的关系得出B′点坐标即可.
【详解】如图,过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
∵点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),
∴,AE=1,EO=2,BE=3.
∴,即,
解得:.
∴
∴点B′的坐标为:.
18.(1)作图详见解析
(2)
【分析】本题考查了位似的性质,平面直角坐标系内三角形面积的求法,
(1)根据相似比的以及点的坐标即可求得;
(2)根据位似的性质可得到的坐标,利用割补法即可求得四边形的面积.
【详解】(1)解:如图所示,即为所求,
(2)解:,
∵与位似,且位似比为;
则,
∴.
.
19.(1)见解析(2)见解析
【分析】(1)根据旋转变换的定义和性质求解可得;
(2)根据位似变换的定义和性质求解可得.
【详解】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△DEF即为所求.
【点睛】本题主要考查作图﹣位似变换与旋转变换,解题的关键是掌握位似变换与旋转变换的定义与性质.
20.补充图形见解析
【分析】先确定位似中心,再根据位似的性质通过作平行画出对应点即可.
【详解】解:如图,分别延长AA′、BB′,它们相交于点O,再过点A作AE∥A′E′交OE′的延长线于E,过点B′作B′C′∥BC′交OC于C′,过点C′作C′D′∥CD交OD于D′,然后连接DE、D′E′即可.
【点睛】本题考查了作图﹣位似变化:先确定位似中心;利用平行确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.
21.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据相似三角形的判定与性质画出△OBC,使△OBC∽△ABO;
(2)根据位似图形的性质以及相似三角形的性质即可画出△ODE;
(3)取格点G,连接BG交AO于点F,根据相似三角形的性质得出.
【详解】(1)如图所示,△OBC即为所求;
(2)如图所示,△ODE即为所求;
(3)如图所示,点F即为所求.
【点睛】本题主要考查了作图-相似变换,熟练掌握相似三角形的判定与性质是解题的关键.
22.(1)见解析
(2)见解析
(3)
【分析】本题考查作图位似变换,平移变换等知识,解题的关键是正确寻找图形,属于中考常考题型.
(1)利用平移变换的性质分别作出A,B,C的对应点,,即可.
(2)根据位似变换的性质分别作出,,的对应点,,即可.
(3)根据点的位置,写出坐标即可.
【详解】(1)解:如图,即为所求.
(2)解:如图,即为所求.
(3)解:若点M是的中点,经过(1)、(2)两次变换,M的对应点的坐标为,
故答案为:.
23.(1)作图见试题解析;(2)等腰直角.
【分析】(1)延长AB到B′,使AB′=2AB,得到B的对应点B′,同样得到C、D的对应点C′,D′,再顺次连接即可;
(2)利用勾股定理求出,,,可以得到AD′=C′D′,,即可判定△AC′D′是等腰直角三角形.
【详解】(1)如图所示:
(2)∵=16+64=80,=36+4=40,=36+4=40,∴AD′=C′D′,,
∴△AC′D′是等腰直角三角形.
故答案为等腰直角.
考点:作图-位似变换.
24.见解析
【分析】在内任意取一点即为O,连接OA、OB、OC,在依次连接OA、OB、OC的中点E、F、D即为所求的三角形.
【详解】如图所示:
【点睛】本题考查位似作图,根据相似比为即可判断新三角形的顶点分别为OA、OB、OC的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.9利用位似放缩图形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知△ABC,任取一点O,连结AO、BO、CO,并取它们的中点D、E、F,得△DEF,则下列说法错误的是( )
A.△ABC与△DEF是位似图形 B.△ABC与△DEF是相似图形
C.△ABC与△DEF的面积之比为4:1 D.△ABC与△DEF的周长之比为4:1
2.在平面直角坐标系中,已知点,,以原点O为位似中心把缩小到原来的则点B的对应点的坐标是( )
A. B.或 C. D.或
3.如图,△A'B'C'是△ABC以点O为位似中心经过位似变换得到的,若AA':OA'=2:3,则下列说法错误的是( )
A.△A'OB'∽△AOB
B.A'B'//AB
C.点O到A'B'与AB的距离之比为3:5
D.△A'B'C'与△ABC的面积之比为3:5
4.2020年是紫禁城建成600年暨故宫博物院成立95周年,在此之前有多个国家曾发行过紫禁城元素的邮品.图1所示的摩纳哥发行的小型张中的图案,以敞开的紫禁城大门和大门内的石狮和太和殿作为邮票和小型张的边饰,如果标记出图1中大门的门框并画出相关的几何图形(图2),我们发现设计师巧妙地使用了数学元素(忽略误差),图2中的四边形与四边形是位似图形,点O是位似中心,点是线段的中点,那么以下结论正确的是( )
A.四边形与四边形的相似比为
B.四边形与四边形的相似比为
C.四边形与四边形的周长比为
D.四边形与四边形的面积比为
5.如图所示,正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E,F,G,H分别是OA,OB,OC,OD的中点,则正方形EFGH与正方形ABCD的面积比是( )
A.1:6 B.1:5 C.1:4 D.1:2
6.如图,在坐标系xOy中,两个南开校徽图标是位似图形,位似中心是点O,①号校徽与②号校徽的位似比为2:1.点在②号校徽上,则在①号校徽上与点M对应的N点坐标为( )
A. B. C. D.
7.已知△ABC与△A1B1C1是位似图形,位似比是1:3,则△ABC与△A1B1C1的面积比( )
A.1 :3 B.1:6 C.1:9 D.3:1
8.如图所示,矩形与矩形是位似图形,点是位似中心,矩形的周长是,,,则和的长分别是
A., B., C., D.,
9.如图,与是位似图形,点O为位似中心,若,则与周长比是( )
A. B. C. D.
10. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,
OC在y轴上,如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的,那么点B′的坐标是【 】
A.(-2,3) B.(2,-3) C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
11.下列说法正确的是( )
A.相等的圆心角所对的弧相等
B.无限小数是无理数
C.阴天会下雨是必然事件
D.在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k
12.如图,网格中每个小正方形的边长都是1,的三个顶点均在格点上,与位似,点为位似中心,且位似比为1:2.若在网格中建立坐标系,点的坐标为,则点的对应点的坐标为( )
A. B.或 C. D.或
二、填空题
13.如图,在平面直角坐标系中,阴影所示的两个正方形是位似图形,若两个正方形在位似中心的异侧,则位似中心的坐标为 .
14.如图,△ABC与△DEF是位似图形,点B的坐标为(3,0),则其位似中心的坐标为 .
15.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,相似比为1:2,把△EFO缩小,则点E的对应点E′的坐标是 .
16.如图,在平面直角坐标系中,以原点O为位似中心,在y轴的同侧作等边三角形,使它与△ABC位似,且相似比为3:1.若四边形是边长为6的菱形,则点A的坐标为 .
17.如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为 .
三、解答题
18.如图,在平面直角坐标系中,的顶点坐标为,,.
(1)以点B为位似中心,在点B的下方画出,使与位似,且位似比为;
(2)求四边形的面积.
19.如图在由边长为1个单位长度的小正方形组成的12×12网格中,已知点A,B,C,D均为网格线的交点
(1)在网格中将△ABC绕点D顺时针旋转90°画出旋转后的图形△A1B1C1;
(2)在网格中将△ABC放大2倍得到△DEF,使A与D为对应点.
20.如图,已知五边形A'B'C'D'E'是五边形的位似图形,但被小玮擦去了一部分,你能将它补完整吗?
21.如图,在6×6的正方形网格中,每个小正方形的边长均为1,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上.按要求完成下列画图.(要求仅用无刻度的直尺,且保留必要的画图痕迹)
(1)在图1中,以BO为边,画出△OBC,使△OBC∽△ABO,C为格点.
(2)在图2中,以点O为位似中心,在网格内画出△ODE,使△ODE与△OAB位似,且位似比k=2,点D、E为格点.
(3)在图3中,在OA边上找一个点F,且满足.
22.如图,在边长为1的小正方形组成的网格中,的顶点在格点(网格线的交点)上,以点O为原点建立平面直角坐标系,点B的坐标为.
(1)将向左平移5个单位长度,得到,画出;
(2)以点O为位似中心,将放大到两倍(即新图与原图的相似比为2),得到,在所给的方格纸中画出;
(3)若点M是的中点,经过(1)、(2)两次变换,M的对应点M2的坐标是 .
23.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
24.已知点O在内,以点O为位似中心画一个三角形,使它与位似,且相似比为.
《9.9利用位似放缩图形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D D C C C B A D
题号 11 12
答案 D D
1.D
【分析】根据位似图形的性质,得出△ABC与△DEF是位似图形进而根据位似图形一定是相似图形得出△ABC与△DEF是相似图形,再根据周长比等于位似比,以及根据面积比等于相似比的平方,即可得出答案.
【详解】解:根据位似性质可得:A、△ABC与△DEF是位似图形,故本选项正确,不符合题意;
△ABC与△DEF是相似图形,故B选项正确,不符合题意;
∵将△ABC的三边缩小到原来的,
∴△ABC与△DEF的周长之比为2:1,故D选项不正确,符合题意;
∵面积比等于相似比的平方,
∴△ABC与△DEF的面积之比为4:1,故C选项正确,不符合题意;
故选:D.
【点睛】本题主要考查了位似图形的性质,正确的记忆位似图形性质是解决问题的关键.
2.D
【分析】本题主要考查了位似变换.在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或.
根据位似变换的性质,把的横纵坐标乘以或,计算即可.
【详解】∵以原点O为位似中心,相似比为,把缩小,点B的坐标为,
∴点B的对应点的坐标为或,
即或.
故选:D.
3.D
【分析】根据位移变换的性质得到,进而求得,根据相似三角形的性质得到,根据相似三角形的面积比等于相似比的平方解答即可.
【详解】△A'B'C'是△ABC以点O为位似中心经过位似变换得到的
AA':OA'=2:3
即点O到A'B'与AB的距离之比为3:5
所以,选项D错误,
故选:D.
【点睛】本题考查的是位似变换的概念、相似三角形的性质,掌握位似与相似的关系、相似三角形的面积比等于相似比的平方是解题的关键.
4.D
【分析】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.两个位似图形必须是相似形;对应点的连线都经过同一点,对应边平行或共线.先利用位似的性质得到,然后根据相似的性质进行判断.
【详解】解:四边形与四边形是位似图形,点是位似中心,点是线段的中点,
,
∴,
四边形与四边形的相似比为,周长的比为,面积比为.
故选:D.
5.C
【分析】由正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,E,F,G,H分别是OA,OB,OC,OD的中点,易求得位似比等于EH:AD=1:2,又由相似三角形面积的比等于相似比的平方,即可求得正方形EFGH与正方形ABCD的面积比.
【详解】∵正方形EFGH是由正方形ABCD经过位似变换得到的,点O是位似中心,
∴正方形EFGH∽正方形ABCD,
∵E,F,G,H分别是OA,OB,OC,OD的中点,
∴EH=AD,
即位似比为:EH:AD=1:2,
∴正方形EFGH与正方形ABCD的面积比是:1:4.
故选C.
【点睛】此题考查位似变换,解题关键在于利用相似的性质进行解答.
6.C
【分析】根据两个图形上对应点的横坐标与横坐标之比等于位似比,纵坐标与纵坐标之比等于位似比求解即可.
【详解】解:∵①号校徽与②号校徽的位似比为2:1.点M( 3, 3)在②号校徽上,
∴在①号校徽上与点M对应的N点坐标为(-6,-6),
故选C.
【点睛】本题主要考查了求位似图形对应点的坐标,熟知两个位似图形上对应点的横坐标与横坐标之比等于位似比,纵坐标与纵坐标之比等于位似比是关键.
7.C
【分析】根据位似图形的面积比等于位似比的平方,即可得到答案.
【详解】∵△ABC与△A1B1C1是位似图形,位似比是1:3,
∴△ABC与△A1B1C1的面积比为1:9,
故选:C.
【点睛】本题主要考查位似图形的性质,熟练掌握位似图形的面积比等于位似比的平方是解题的关键.
8.B
【分析】根据矩形的性质得到,根据位似变换的性质得到,根据平行线分线段成比例定理列出比例式,代入计算得到答案.
【详解】解:∵矩形ABCD的周长是24,
∴,
∴,
∵,,
∴,
∵矩形ABCD与矩形是位似图形,
∴,
∴,,
∴,即,
解得,,
则,
故选:B.
【点睛】本题考查了位似图形的性质,熟练掌握位似图形的任意一对对应点与位似中心在同一直线上,它们到位似中心的距离之比等于相似比是解答本题的关键.也考查了平行线分线段成比例定理.
9.A
【分析】根据位似图形是相似图形,相似三角形的周长比等于相似比,进行求解即可.
【详解】解:∵与是位似图形,
∴,
∵,
∴相似比为:,
∴与周长比等于相似比;
故选A.
【点睛】本题考查相似三角形的性质.熟练掌握位似图形是相似图形,相似三角形的周长比等于相似比,是解题的关键.
10.D
【详解】如果两个图形不仅是相似图形,而且每组对应点的连线交于一点,对应边互相平行或在一
条直线上,那么这两个图形叫做位似图形.把一个图形变换成与之位似的图形是位似变换.因此,
∵矩形OA′B′C′与矩形OABC关于点O位似,∴矩形OA′B′C′∽矩形OABC.
∵矩形OA′B′C′的面积等于矩形OABC面积的,∴位似比为:.
∵点B的坐标为(-4,6),∴点B′的坐标是:(-2,3)或(2,-3).故选D.
11.D
【分析】根据圆周角定理以及无理数的定义和随机事件的定义和位似图形的性质分别判断得出答案即可.
【详解】解: A、根据必须是同圆或等圆中,相等的圆心角所对的弧才相等,故此选项错误;
B、无限不循环小数是无理数,无限循环小数是有理数,故此选项错误;
C、阴天会下雨是随机事件,故此选项错误;
D、根据位似图形的性质得出:在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k,故此选项正确.
故选:D.
12.D
【分析】根据位似变换的概念和性质、结合图形解答.
【详解】解:如图,
由图可知,点C的坐标为(-2,3),
以点A为位似中心,在网格中画,使与△ABC位似,且位似比为1:2,
则点的坐标为(-5,0)或(-1,4),
故选:D.
【点睛】本题考查位似变换的应用,熟练掌握位似变换的概念和性质是解题关键.
13.
【分析】连接各组对应点,它们在两个正方形之间相交于点,则点为位似中心,然后写出点坐标即可.
【详解】解:如图,点为位似中心,.
故答案为:.
【点睛】本题考查位似变换:位似的两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行(或共线),掌握位似变换的性质是解题的关键.
14.(1,0)
【详解】分析:利用△ABC与△DEF是位似图形,连接图上对应三点的坐标,连线的交点就是位似中心.
详解:
连接各对应点A,D,与C,F,交点Q即是位似中心的坐标,
∴其位似中心的坐标为:(1,0),
故答案为(1,0).
点睛:本题考查了位似图形的位似中心的确定方法.顺次连接各对应点得出位似中心是解决问题的关键.
15.(-2,1)或(2,-1).
【分析】根据已知得出位似图形对应坐标与位似图形比的关系进而得出答案.
【详解】解:∵顶点E的坐标是(-4,2),以原点O为位似中心相似比为1:2将△EFO缩小得到它的位似图形△E′F′O,
∴点E′的坐标是:(×(-4),×2),[- ×(-4),- ×2],
即(-2,1)或(2,-1).
故答案为(-2,1)或(2,-1).
【点睛】本题考查位似图形的性质,根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k得出是解题的关键.
16.
【分析】根据菱形的性质、等边三角形的性质求出,通过相似比即可得A的坐标.
【详解】解:若四边形是边长为6的菱形,.
∵是等边三角形
∴
则
∵,且相似比为3:1
∴
故答案为:
【点睛】本题主要考查菱形的性质、等边三角形的性质、位似图形的性质,掌握相关知识并灵活应用是解题的关键.
17..
【分析】根据位似图形的性质画出图形,利用对应边之间的关系得出B′点坐标即可.
【详解】如图,过点B作BE⊥x轴于点E,B′作B′F⊥x轴于点F,
∵点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于的A的位似图形,且O′的坐标为(﹣1,0),
∴,AE=1,EO=2,BE=3.
∴,即,
解得:.
∴
∴点B′的坐标为:.
18.(1)作图详见解析
(2)
【分析】本题考查了位似的性质,平面直角坐标系内三角形面积的求法,
(1)根据相似比的以及点的坐标即可求得;
(2)根据位似的性质可得到的坐标,利用割补法即可求得四边形的面积.
【详解】(1)解:如图所示,即为所求,
(2)解:,
∵与位似,且位似比为;
则,
∴.
.
19.(1)见解析(2)见解析
【分析】(1)根据旋转变换的定义和性质求解可得;
(2)根据位似变换的定义和性质求解可得.
【详解】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△DEF即为所求.
【点睛】本题主要考查作图﹣位似变换与旋转变换,解题的关键是掌握位似变换与旋转变换的定义与性质.
20.补充图形见解析
【分析】先确定位似中心,再根据位似的性质通过作平行画出对应点即可.
【详解】解:如图,分别延长AA′、BB′,它们相交于点O,再过点A作AE∥A′E′交OE′的延长线于E,过点B′作B′C′∥BC′交OC于C′,过点C′作C′D′∥CD交OD于D′,然后连接DE、D′E′即可.
【点睛】本题考查了作图﹣位似变化:先确定位似中心;利用平行确定能代表所作的位似图形的关键点;最后顺次连接上述各点,得到放大或缩小的图形.
21.(1)见解析
(2)见解析
(3)见解析
【分析】(1)根据相似三角形的判定与性质画出△OBC,使△OBC∽△ABO;
(2)根据位似图形的性质以及相似三角形的性质即可画出△ODE;
(3)取格点G,连接BG交AO于点F,根据相似三角形的性质得出.
【详解】(1)如图所示,△OBC即为所求;
(2)如图所示,△ODE即为所求;
(3)如图所示,点F即为所求.
【点睛】本题主要考查了作图-相似变换,熟练掌握相似三角形的判定与性质是解题的关键.
22.(1)见解析
(2)见解析
(3)
【分析】本题考查作图位似变换,平移变换等知识,解题的关键是正确寻找图形,属于中考常考题型.
(1)利用平移变换的性质分别作出A,B,C的对应点,,即可.
(2)根据位似变换的性质分别作出,,的对应点,,即可.
(3)根据点的位置,写出坐标即可.
【详解】(1)解:如图,即为所求.
(2)解:如图,即为所求.
(3)解:若点M是的中点,经过(1)、(2)两次变换,M的对应点的坐标为,
故答案为:.
23.(1)作图见试题解析;(2)等腰直角.
【分析】(1)延长AB到B′,使AB′=2AB,得到B的对应点B′,同样得到C、D的对应点C′,D′,再顺次连接即可;
(2)利用勾股定理求出,,,可以得到AD′=C′D′,,即可判定△AC′D′是等腰直角三角形.
【详解】(1)如图所示:
(2)∵=16+64=80,=36+4=40,=36+4=40,∴AD′=C′D′,,
∴△AC′D′是等腰直角三角形.
故答案为等腰直角.
考点:作图-位似变换.
24.见解析
【分析】在内任意取一点即为O,连接OA、OB、OC,在依次连接OA、OB、OC的中点E、F、D即为所求的三角形.
【详解】如图所示:
【点睛】本题考查位似作图,根据相似比为即可判断新三角形的顶点分别为OA、OB、OC的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
