第六章特殊平行四边形同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
第六章特殊平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,GH折叠,使点B和点C都落在点P处,若∠BFE+∠CGH=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
2.如图所示,将一矩形纸片沿AB折叠,已知,则( )
A.48° B.66° C.72° D.78°
3.如图,用平移法说明平行四边形的面积公式时, 若平移到,,,则的平移距离为( )
A.1 B.3 C.4 D.5
4.如图,正方形ABCD中AB=6,点E在CD上,且CD=3DE,将沿AE对折至,延长边EF交边BC于点G,连接AG、CF.下列结论:①;②;③;④;⑤,其中正确结论的个数是( )个
A.2 B.3 C.4 D.5
5.如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
6.如图,矩形沿对角线折叠,已知长,宽,那么折叠后重合部分的面积是( )
A. B. C. D.
7.如图,在菱形中,E是的中点,F是的中点,连接.如果,那么的长为( )
A.4 B.8 C.16 D.32
8.如图,菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24
C.28 D.40
9.如图,在四边形中,,,连接与交于点O,若,,则四边形的面积为( )
A.24 B.36 C.48 D.60
10.下列命题中,正确的命题的是( )
A.有两边相等的平行四边形是菱形 B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形 D.两条对角线相等的四边形是矩形
11.如图,是的高,分别是三边中点,则与的大小关系是( )
A. B. C. D.不能确定
12.如图,在中,下列条件中不能使成为菱形的是( )
A. B. C. D.
二、填空题
13.把一张长方形纸条ABCD沿EF折叠,若∠AEG=62°,则∠DEF= °.
14.如图,四边形纸片ABCD中,,,,,点E在BC上,且.将四边形纸片ABCD沿AE折叠,点C、D分别落在点、处,与AB交于点F,则BF长为 .
15.在矩形中,对角线与交于点,请添加一个条件: 使得矩形是正方形.(只写一个)
16.在中,于点D,交于点E,交于点F,当满足条件 时,四边形是矩形.
17.如图,, 是正方形 的边 上的两个动点,满足 ,连接 交 于点 ,连接 交 于点 ,连接 ,若正方形的边长为 ,则线段 的最小值是 .
三、解答题
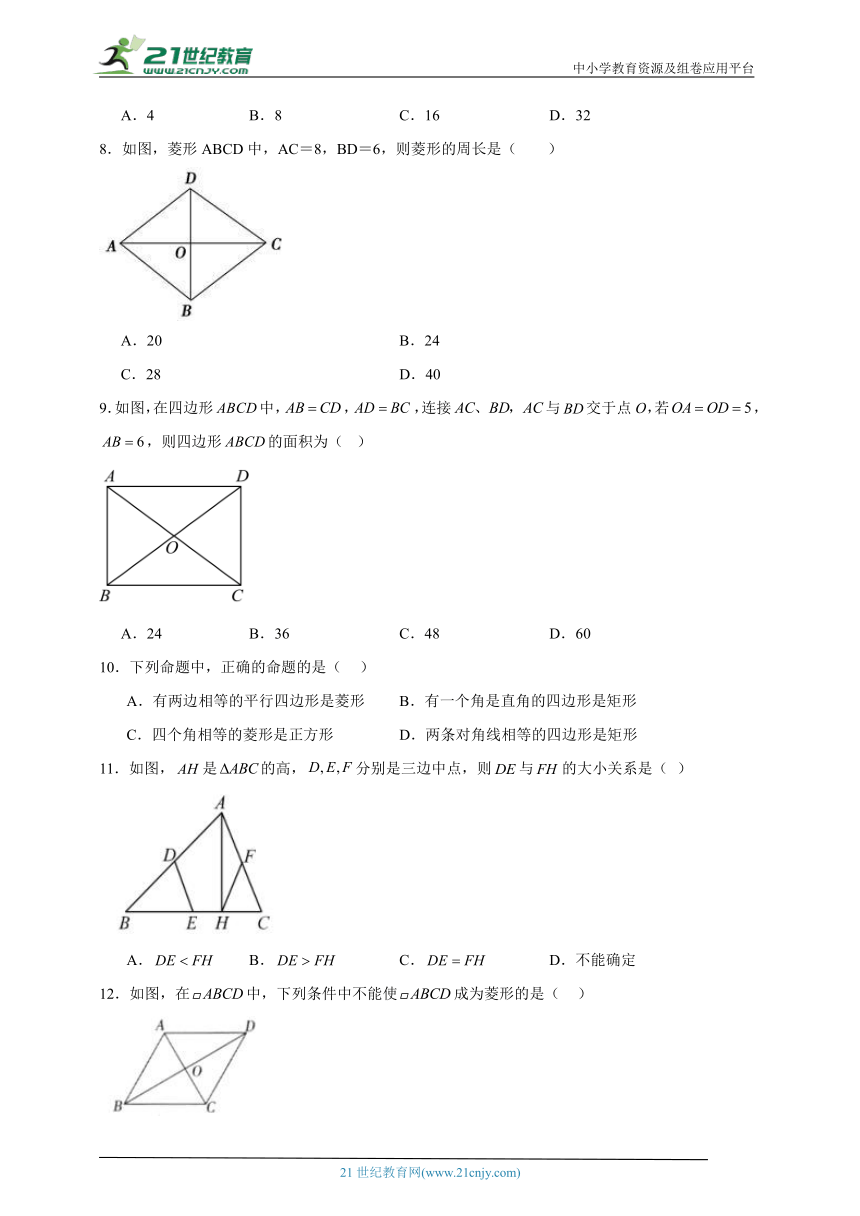
18.如图,在平面直角坐标系中,正方形的顶点A的坐标为,对角线轴于点C,点D在y轴上.
(1)求点B的坐标;
(2)求直线的解析式.
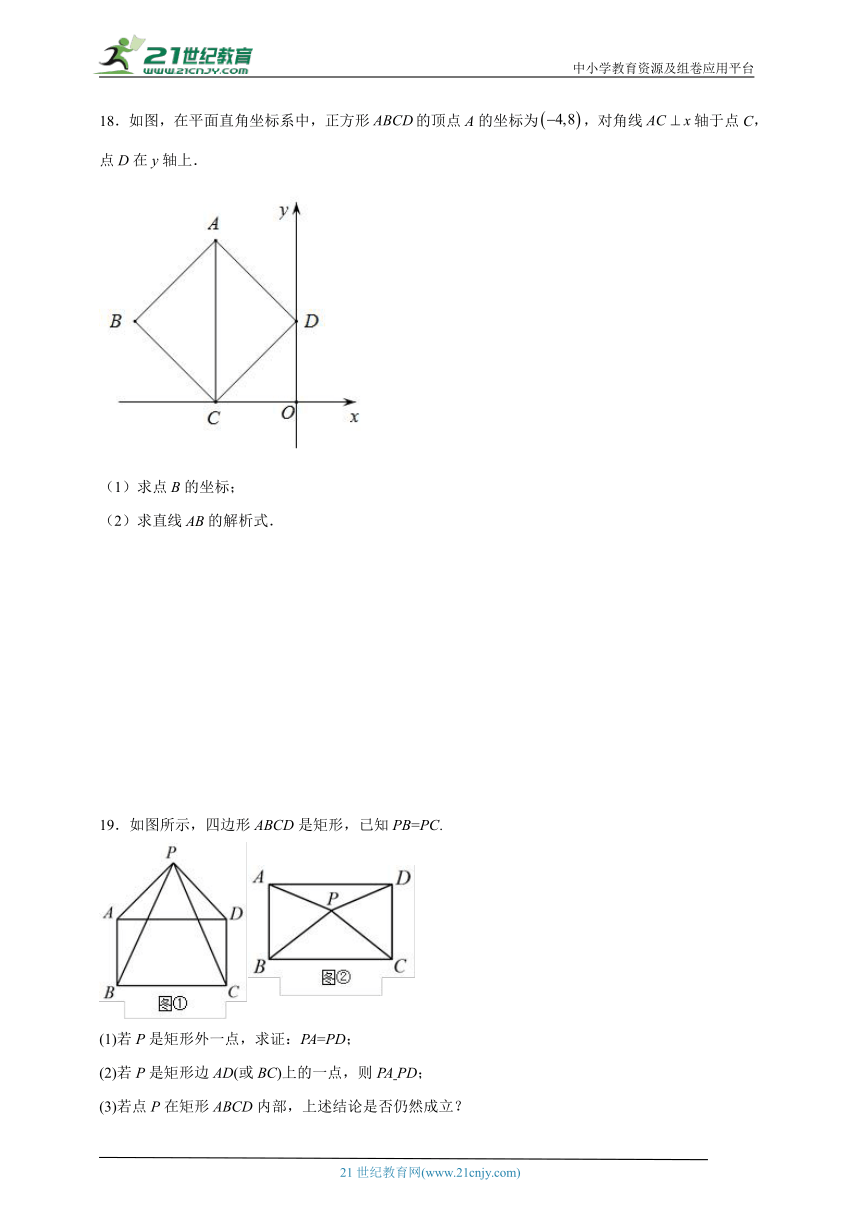
19.如图所示,四边形ABCD是矩形,已知PB=PC.
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
20.如图所示,点和点分别在正方形的边上,且为边的中点,,连接,,,试判断的形状,并说明理由.
21.如图,已知矩形纸片,,,.按以下步骤操作:
第一步:对折矩形纸片,使与重合,得到折痕,把纸片展平.
第二步:再一次折叠纸片,使点A落在上,并使折痕经过点B,得到折痕,同时得到了线段.
(1)求线段的长;
(2)通过观察猜测的度数是多少?并进行证明;
(3)在四边形中,点P、Q同时从B点出发,分别作匀速运动,点P沿以每秒1个单位向终点C运动,点Q沿、以每秒2个单位向终点D运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
①设两点从点B开始运动了x秒,当时,点Q在什么位置?
②两点在运动的过程中,是否存在四边形为菱形?如果存在,求出x的值;如果不存在,请说明理由.
22. 求证:矩形的对角线相等.
23.已知:平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.求证:
(1)BE⊥AC;
(2)EG=EF.
24.如图将边长为4的正方形纸片ABCD折叠,使B点落在CD边上一点E,压平后得到折痕MN,当.
(1)求NE的长;
(2)连AN、AE,NG⊥AE,垂足为G,求GN的长;
(3)直接写出AM的长度.
《第六章特殊平行四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C B A C B A C C
题号 11 12
答案 C A
1.C
【分析】由折叠可得EF,GH分别是∠BFP和∠CGP的角平分线,可得∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,进而根据平角定义及三角形内角和180°可得∠FPG的度数.
【详解】解:由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
【点睛】本题考查矩形与折叠、角平分线的性质、两直线平行内错角相等等知识,是重要考点,掌握相关知识是解题关键.
2.C
【分析】由折叠及矩形的性质可得,再根据平行线的性质求出,根据周角的定义求解即可.
【详解】∵将一矩形纸片沿AB折叠,
∴,
,
,
,
,
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质及平行线的性质,熟练掌握知识点是解题的关键.
3.C
【分析】本题考查了平行四边形的性质,平移的性质,根据平移的性质结合矩形的面积公式即可得到结论.
【详解】解:∵四边形是平行四边形,
∴,
∵,
∴,
∴四边形是矩形,
由平移的性质得,
∴,
∴平行四边形的面积=矩形的面积,
∴的平移距离为4.
故选:C.
4.B
【分析】先根据正方形的性质可得,再根据折叠的性质可得,从而可得,然后利用直角三角形全等的判定定理即可判断①;先根据全等三角形的性质可得,设,则,再在中,利用勾股定理求出的值,由此即可判断②;先根据等腰三角形的性质可得,再根据三角形的内角和定理可得,根据平角的定义可得,从而可得,然后根据平行线的判定即可判断③;根据线段的长度可得,再根据三角形的面积公式可得,由此即可判断④;根据线段的长度分别求出和的值,由此即可判断⑤.
【详解】解:四边形是正方形,且,
,
,
,
由折叠的性质得:,
,
在和中,,
,结论①正确;
,
设,则,
在中,,即,
解得,
,
,结论②正确;
,
,
又,
,
,结论③正确;
,
,
,
,
,结论④错误;
,
,
,
,结论⑤错误;
综上,正确结论的个数是3个,
故选:B.
【点睛】本题考查了正方形的性质、折叠的性质、直角三角形全等的判定定理与性质、勾股定理等知识点,熟练掌握正方形的性质和折叠的性质是解题关键.
5.A
【分析】利用中位线、菱形、矩形的性质可知,每一次操作后得到的四边形面积为原四边形面积的一半,由此可解.
【详解】解:如图,连接AC,BD,,.
∵ 四边形ABCD是矩形,
∴,,.
∵ ,,,分别是矩形四个边的中点,
∴,
∴,
∴四边形是菱形,
∵ ,,
∴四边形的面积为:.
同理,由中位线的性质可知,
,,
,,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形,
∴四边形的面积为:.
∴每一次操作后得到的四边形面积为原四边形面积的一半,
∴四边形的面积是.
故选:A.
【点睛】本题考查矩形的性质,菱形的性质以及中位线的性质,证明四边形是菱形,四边形是矩形是解题的关键.
6.C
【分析】由矩形的性质易得,那么可用表示出,利用的三边关系即可求得长,然后三角形面积公式求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∵
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质,解决此类问题,应利用折叠找到相应的直角三角形,利用勾股定理求得所需线段长度.
7.B
【分析】本题考查了三角形的中位线性质、菱形的性质.熟练掌握三角形的中位线性质、菱形的性质是解题的关键.
根据三角形的中位线性质求出,再根据菱形的性质即可求解.
【详解】解:在中,E是的中点,F是的中点,
,
,
,
,
四边形是菱形,
.
故选B.
8.A
【详解】设对角线的交点为O,∵四边形ABCD是菱形,AC=8,BD=6,∴∠AOD=90°,AO=4,DO=3,∴,∴周长为5×4=20,故选A.
9.C
【分析】本题考查了矩形的判定与性质,勾股定理,得到四边形是矩形是解题的关键.
先证明四边形是矩形,得到,再运用勾股定理即可求解,继而得到矩形的面积.
【详解】解:∵在四边形中,,,
∴四边形是平行四边形,
∴,
∴,
∴四边形是矩形,
∴,
∴,
∴矩形的面积为,
故选:C.
10.C
【分析】利用菱形的判定、矩形的判定、正方形的判定定理分别判断后即可确定正确的选项.
【详解】解:A、有两邻边相等的平行四边形是菱形,故原命题错误;
B、有一个角是直角的平行四边形是矩形,故原命题错误;
C、四个角相等的菱形是正方形,故原命题正确;
D、两条对角线相等的平行四边形是矩形,故原命题错误,
故选:C.
【点睛】本题考查了命题与定理的知识,解题的关键是了解特殊的平行四边形的判定方法,难度不大.
11.C
【分析】根据三角形中位线定理和直角三角形的性质可DE=AC,FH=AC,最后运用等量代换即可解答.
【详解】解:∵ D,E分别是AB,BC的中点,
∴DE=AC,
∵F为AC的中点,是的高
∴FH=AC
∴DE=FH.
故选:C.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线等于第三边的一半是解答本题的关键.
12.A
【分析】根据菱形的判定逐项分析即可.
【详解】解:A. 不能使成为菱形,符合题意;
B.根据一组邻边相等的平行四边形是菱形可得是菱形,故不符合题意;
C. 根据对角线互相垂直的平行四边形是菱形可得是菱形,故不符合题意;
D. 根据对角线互相垂直的平行四边形是菱形可得是菱形,故不符合题意,
故选A.
【点睛】本题考查了菱形的判定定理,注意:菱形的判定定理有:①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形,④对角线平分一组对角的平行四边形是菱形.
13.59°
【分析】根据折叠的性质,得到,再根据平行线的性质得到,求出解决即可.
【详解】解:∵把一张长方形纸片ABCD沿EF折叠
则
故答案是59°.
【点睛】本题考查了折叠的性质以及平行线的性质,解决本题的关键是熟练掌握折叠与平行线的性质,找到相等的角.
14.5
【分析】根据折叠的性质可得,则,勾股定理求得,证明,即可求得.
【详解】解:∵,,,,
∴四边形是矩形,
,
将四边形纸片ABCD沿AE折叠,点C、D分别落在点、处,
,
,
,
中,
,
,
又
故答案为:5
【点睛】本题考查了折叠的性质,矩形的判定,勾股定理,全等三角形的性质与判定,掌握折叠的性质与勾股定理是解题的关键.
15.(答案不唯一)
【分析】本题考查正方形的判定,解题的关键是掌握:有一组邻边相等或对角线互相垂直的矩形是正方形.据此解答即可.
【详解】解:.
理由:∵四边形是矩形,
又∵,
∴四边形是正方形.
故答案为:(答案不唯一).
16.
【分析】先证四边形是平行四边形,再证,即可得出结论.本题考查矩形的判定、平行四边形的判定与性质、等知识,熟练掌握菱矩形的判定和平行四边形的判定与性质.
【详解】证明:,,
四边形是平行四边形,,
当时
∴四边形是矩形
∴当满足条件时,四边形是矩形
故答案为:
17.
【分析】根据正方形的性质可得,,然后利用证明和全等,根据全等三角形对应角相等可得,利用证明和全等,根据全等三角形对应角相等可得,从而得到,然后求出,取的中点O,连接OF、,根据直角三角形斜边上的中线等于斜边的一半可得,利用勾股定理列式求出,然后根据三角形的三边关系可知当O、F、C三点共线时,的长度最小.
【详解】解:在正方形中,,,,
在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∴,
取的中点O,连接,
则,
在中,,
根据三角形的三边关系,,
∴当O、F、C三点共线时,的长度最小,
最小值.
故答案为:.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出CF最小时点F的位置是解题关键,也是本题的难点.
18.(1)点B的坐标为;(2)直线的解析式为.
【分析】(1)由正方形的性质可以得到对角线之间的关系,进而得到坐标;
(2)已知两点坐标,用待定系数法求直线解析式.
【详解】解:(1)如图,连接,过点B作轴,点E为垂足,
∵四边形是正方形,
∴,,
故点B的坐标为;
(2)设直线的解析式为,
则,解得.
故直线的解析式为.
【点睛】本题考查了正方形的性质、坐标的表示、待定系数法求一次函数解析式,难度不大.
19.(1)详见解析;(2)=;(3)成立,理由详见解析.
【分析】(1)由四边形ABCD是矩形,可得AB=DC,∠ABC=∠DCB=90°,又由PB=PC可得∠PBC=∠PCB,求出∠PBA=∠PCD,进而利用SAS证明△APB≌△DPC即可得到PA=PD;
(2)当P是矩形边AD(或BC)上的一点,通过HL可证Rt△APB≌Rt△DPC,得到PA=PD;
(3)当点P在矩形ABCD内部时,同(1)可证△APB≌△DPC,得到PA=PD.
【详解】(1)证明:如图①,
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,,
∴△APB≌△DPC,
∴PA=PD;
(2) 如图②,当P是矩形边AD上的一点,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,PB=PC,
∴Rt△APB≌Rt△DPC(HL),
∴PA=PD,
当P是矩形边BC上的一点,同理可得:PA=PD,
∴若P是矩形边AD(或BC)上的一点,则PA=PD;
(3)成立.
理由如下:
如图③,
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,,
∴△APB≌△DPC,
∴PA=PD.
【点睛】此题考查了矩形的性质以及全等三角形的判定和性质,难度适中,根据矩形的性质得到判定全等的条件是解决问题的关键.
20.是直角三角形,且.
【分析】设正方形的边长为x,得到,,.
然后分别利用勾股定理求出,最后得到,即可解答.
【详解】是直角三角形,理由如下:
设正方形的边长为x.
因为点是边的中点,所以.
又因为,所以,.
在中,根据勾股定理,
得.
在中,根据勾股定理,
得.
在中,根据勾股定理,
得.
因为,
所以为直角三角形,且.
【点睛】此题考查勾股定理的逆定理,正方形的性质,解题关键在于列出方程.
21.(1)
(2),证明见解析
(3)①当时,点在点处;②存在,
【分析】(1)根据勾股定理即可求出;
(2)连接,通过证明为等边三角形,即可求解;
(3)①先求出时,点Q所走路程,即可得出点Q的位置;②根据菱形的性质可得,,求出点P和点Q运动的时间,若相等,则存在,否则,不存在.
【详解】(1)解:∵四边形为矩形,
∴,
∵,,
∴;
(2)猜测:,
证明:连接,
∵为折痕,
∴垂直平分,
∴,
∵由折叠所得,
∴,
∴,则为等边三角形,
∴,
∴;
(3)解:①当时,点Q所走路程为:;
∵,
∴当时,点在点处.
②存在,
∵四边形是菱形,,
∴,
∴点Q所走路程为:;点P所走路程为;
∴点Q行走的时间(秒),点P行走的时间(秒),
∵点Q行走的时间=点P行走的时间,
∴存在,当时,四边形是菱形.
【点睛】本题主要考查了勾股定理,等边三角形的判定和性质,菱形的判定和性质,解题的关键是掌握直角三角形两直角边平方和等于斜边的平方,等边三角形三个内角都是,菱形是四条边都相等.
22.见解析
【详解】已知:四边形ABCD是矩形,AC与BD是对角线,
求证:AC=BD.
证明: ∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
又∵BC=CB,
∴△ABC≌△DCB,
∴AC=BD.
所以矩形的对角线相等.
23.(1)证明见解析;(2)证明见解析.
【分析】(1)由已知条件易证△OBC是等腰三角形,E是OC的中点,根据等腰三角形中底边上的高与中线合一的性质知BE⊥AC.
(2)利用直角三角形中斜边上的中线等于斜边的一半及中位线定理可证EG=EF.
【详解】解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,BD=2BO.
由已知BD="2AD,"
∴BO=BC.
又E是OC中点,
∴BE⊥AC.
(2)由(1)BE⊥AC,又G是AB中点,
∴EG是Rt△ABE斜边上的中线.
∴EG=AB
又∵EF是△OCD的中位线,
∴EF=CD.
又AB="CD,"
∴EG=EF.
【点睛】本题考查1.三角形中位线定理;2.等腰三角形的判定与性质;3.直角三角形斜边上的中线;4.平行四边形的性质.
24.(1)NE=2.5;
(2)NG=;
(3)AM=0.5.
【分析】(1)由折叠性质可得EN=BN,由题意可得CE=DE,在Rt△CEN中,利用勾股定理求解即可;
(2)利用正方形面积减去△ABN,△ADE和△CEN的面积可得△AEN的面积,利用勾股定理可得AE,利用三角形面积公式即可求解;
(3)连接BM,EM,由折叠性质可得AM=FM,AB=EF,∠BAD=∠EFM,可证得△ABM≌△FEM,从而得到BM=EM,在Rt△ABM和Rt△DEM中,设AM=x,则DM=4-x,利用勾股定理分别表示出BM,EM,利用等量关系构造方程即可求解.
【详解】(1)解:∵四边形ABCD为正方形,
∴∠C=90°,
∵,BC=CD=4,
∴CE=DE=2,
由折叠性质可得:EN=BN,
设EN=x,则BN=x,
∴CN=BC-BN=4-x,
在Rt△CEN中,由勾股定理可得:NE2=CN2+CE2,
即x2=(4-x)2+22,
解得:x=2.5,
∴NE=2.5;
(2)解:在Rt△ADE中,由勾股定理可得:
AE= ,
由(1)可得NE=2.5,
∴BN=2.5,
∴CN=BC-BN=1.5,
∵S ABCD=BC×CD=16,S△ABN=×AB×BN=×4×2.5=5,
S△CEN=×CN×CE=×1.5×2=1.5,S△ADE=×AD×DE=×4×2=4,
∴S△AEN=S ABCD-S△ABN-S△CEN-S△ADE=16-5-1.5-4=5.5,
∵NG⊥AE,
∴S△AEN=×AE×NG,
即5.5=×2×NG,
∴NG=;
(3)解:如图,连接BM,EM,
由折叠性质可得:
AM=FM,AB=EF,∠BAM=∠EFM,
∴△ABM≌△FEM(SAS),
∴BM=EM,
设AM=x,则DM=4-x,
在Rt△ABM中,由勾股定理可得:
BM2=AB2+AM2,即BM2=42+x2,
在Rt△DEM中,由勾股定理可得:
EM2=DM2+DE2,即EM2=(4-x)2+22,
∵BM=EM,
∴BM2=EM2,
∴42+x2=(4-x)2+22,
解得:x=0.5,
∴AM=0.5.
【点睛】本题考查折叠的性质,正方形的性质,勾股定理等知识点,解题的关键是明确折叠的性质:折叠是一种对称变换,属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章特殊平行四边形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知长方形纸片ABCD,点E,H在AD边上,点F,G在BC边上,GH折叠,使点B和点C都落在点P处,若∠BFE+∠CGH=118°,则∠FPG的度数为( )
A.54° B.55° C.56° D.57°
2.如图所示,将一矩形纸片沿AB折叠,已知,则( )
A.48° B.66° C.72° D.78°
3.如图,用平移法说明平行四边形的面积公式时, 若平移到,,,则的平移距离为( )
A.1 B.3 C.4 D.5
4.如图,正方形ABCD中AB=6,点E在CD上,且CD=3DE,将沿AE对折至,延长边EF交边BC于点G,连接AG、CF.下列结论:①;②;③;④;⑤,其中正确结论的个数是( )个
A.2 B.3 C.4 D.5
5.如图,已知矩形ABCD的边长分别为a,b,进行如下操作:第一次,顺次连接矩形ABCD各边的中点,得到四边形;第二次,顺次连接四边形各边的中点,得到四边形;…如此反复操作下去,则第n次操作后,得到四边形的面积是( )
A. B. C. D.
6.如图,矩形沿对角线折叠,已知长,宽,那么折叠后重合部分的面积是( )
A. B. C. D.
7.如图,在菱形中,E是的中点,F是的中点,连接.如果,那么的长为( )
A.4 B.8 C.16 D.32
8.如图,菱形ABCD中,AC=8,BD=6,则菱形的周长是( )
A.20 B.24
C.28 D.40
9.如图,在四边形中,,,连接与交于点O,若,,则四边形的面积为( )
A.24 B.36 C.48 D.60
10.下列命题中,正确的命题的是( )
A.有两边相等的平行四边形是菱形 B.有一个角是直角的四边形是矩形
C.四个角相等的菱形是正方形 D.两条对角线相等的四边形是矩形
11.如图,是的高,分别是三边中点,则与的大小关系是( )
A. B. C. D.不能确定
12.如图,在中,下列条件中不能使成为菱形的是( )
A. B. C. D.
二、填空题
13.把一张长方形纸条ABCD沿EF折叠,若∠AEG=62°,则∠DEF= °.
14.如图,四边形纸片ABCD中,,,,,点E在BC上,且.将四边形纸片ABCD沿AE折叠,点C、D分别落在点、处,与AB交于点F,则BF长为 .
15.在矩形中,对角线与交于点,请添加一个条件: 使得矩形是正方形.(只写一个)
16.在中,于点D,交于点E,交于点F,当满足条件 时,四边形是矩形.
17.如图,, 是正方形 的边 上的两个动点,满足 ,连接 交 于点 ,连接 交 于点 ,连接 ,若正方形的边长为 ,则线段 的最小值是 .
三、解答题
18.如图,在平面直角坐标系中,正方形的顶点A的坐标为,对角线轴于点C,点D在y轴上.
(1)求点B的坐标;
(2)求直线的解析式.
19.如图所示,四边形ABCD是矩形,已知PB=PC.
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
20.如图所示,点和点分别在正方形的边上,且为边的中点,,连接,,,试判断的形状,并说明理由.
21.如图,已知矩形纸片,,,.按以下步骤操作:
第一步:对折矩形纸片,使与重合,得到折痕,把纸片展平.
第二步:再一次折叠纸片,使点A落在上,并使折痕经过点B,得到折痕,同时得到了线段.
(1)求线段的长;
(2)通过观察猜测的度数是多少?并进行证明;
(3)在四边形中,点P、Q同时从B点出发,分别作匀速运动,点P沿以每秒1个单位向终点C运动,点Q沿、以每秒2个单位向终点D运动.当这两点中有一点到达自己的终点时,另一点也停止运动.
①设两点从点B开始运动了x秒,当时,点Q在什么位置?
②两点在运动的过程中,是否存在四边形为菱形?如果存在,求出x的值;如果不存在,请说明理由.
22. 求证:矩形的对角线相等.
23.已知:平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E,F,G分别是OC,OD,AB的中点.求证:
(1)BE⊥AC;
(2)EG=EF.
24.如图将边长为4的正方形纸片ABCD折叠,使B点落在CD边上一点E,压平后得到折痕MN,当.
(1)求NE的长;
(2)连AN、AE,NG⊥AE,垂足为G,求GN的长;
(3)直接写出AM的长度.
《第六章特殊平行四边形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C C C B A C B A C C
题号 11 12
答案 C A
1.C
【分析】由折叠可得EF,GH分别是∠BFP和∠CGP的角平分线,可得∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,进而根据平角定义及三角形内角和180°可得∠FPG的度数.
【详解】解:由折叠可知:
EF,GH分别是∠BFP和∠CGP的角平分线,
∴∠PFE=∠BFE,∠PGH=∠CGH,
∴∠PFE+∠PGH=∠BFE+∠CGH=118°,
∴∠BFP+∠CGP=2(∠BFE+∠CGH)=236°,
∴∠PFG+∠PGF=360°﹣(∠BFP+∠CGP)=360°﹣236°=124°,
∴∠FPG=180°﹣(∠PFG+∠PGF)=180°﹣124°=56°.
故选:C.
【点睛】本题考查矩形与折叠、角平分线的性质、两直线平行内错角相等等知识,是重要考点,掌握相关知识是解题关键.
2.C
【分析】由折叠及矩形的性质可得,再根据平行线的性质求出,根据周角的定义求解即可.
【详解】∵将一矩形纸片沿AB折叠,
∴,
,
,
,
,
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质及平行线的性质,熟练掌握知识点是解题的关键.
3.C
【分析】本题考查了平行四边形的性质,平移的性质,根据平移的性质结合矩形的面积公式即可得到结论.
【详解】解:∵四边形是平行四边形,
∴,
∵,
∴,
∴四边形是矩形,
由平移的性质得,
∴,
∴平行四边形的面积=矩形的面积,
∴的平移距离为4.
故选:C.
4.B
【分析】先根据正方形的性质可得,再根据折叠的性质可得,从而可得,然后利用直角三角形全等的判定定理即可判断①;先根据全等三角形的性质可得,设,则,再在中,利用勾股定理求出的值,由此即可判断②;先根据等腰三角形的性质可得,再根据三角形的内角和定理可得,根据平角的定义可得,从而可得,然后根据平行线的判定即可判断③;根据线段的长度可得,再根据三角形的面积公式可得,由此即可判断④;根据线段的长度分别求出和的值,由此即可判断⑤.
【详解】解:四边形是正方形,且,
,
,
,
由折叠的性质得:,
,
在和中,,
,结论①正确;
,
设,则,
在中,,即,
解得,
,
,结论②正确;
,
,
又,
,
,结论③正确;
,
,
,
,
,结论④错误;
,
,
,
,结论⑤错误;
综上,正确结论的个数是3个,
故选:B.
【点睛】本题考查了正方形的性质、折叠的性质、直角三角形全等的判定定理与性质、勾股定理等知识点,熟练掌握正方形的性质和折叠的性质是解题关键.
5.A
【分析】利用中位线、菱形、矩形的性质可知,每一次操作后得到的四边形面积为原四边形面积的一半,由此可解.
【详解】解:如图,连接AC,BD,,.
∵ 四边形ABCD是矩形,
∴,,.
∵ ,,,分别是矩形四个边的中点,
∴,
∴,
∴四边形是菱形,
∵ ,,
∴四边形的面积为:.
同理,由中位线的性质可知,
,,
,,
∴四边形是平行四边形,
∵,
∴,
∴四边形是矩形,
∴四边形的面积为:.
∴每一次操作后得到的四边形面积为原四边形面积的一半,
∴四边形的面积是.
故选:A.
【点睛】本题考查矩形的性质,菱形的性质以及中位线的性质,证明四边形是菱形,四边形是矩形是解题的关键.
6.C
【分析】由矩形的性质易得,那么可用表示出,利用的三边关系即可求得长,然后三角形面积公式求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∵
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质,解决此类问题,应利用折叠找到相应的直角三角形,利用勾股定理求得所需线段长度.
7.B
【分析】本题考查了三角形的中位线性质、菱形的性质.熟练掌握三角形的中位线性质、菱形的性质是解题的关键.
根据三角形的中位线性质求出,再根据菱形的性质即可求解.
【详解】解:在中,E是的中点,F是的中点,
,
,
,
,
四边形是菱形,
.
故选B.
8.A
【详解】设对角线的交点为O,∵四边形ABCD是菱形,AC=8,BD=6,∴∠AOD=90°,AO=4,DO=3,∴,∴周长为5×4=20,故选A.
9.C
【分析】本题考查了矩形的判定与性质,勾股定理,得到四边形是矩形是解题的关键.
先证明四边形是矩形,得到,再运用勾股定理即可求解,继而得到矩形的面积.
【详解】解:∵在四边形中,,,
∴四边形是平行四边形,
∴,
∴,
∴四边形是矩形,
∴,
∴,
∴矩形的面积为,
故选:C.
10.C
【分析】利用菱形的判定、矩形的判定、正方形的判定定理分别判断后即可确定正确的选项.
【详解】解:A、有两邻边相等的平行四边形是菱形,故原命题错误;
B、有一个角是直角的平行四边形是矩形,故原命题错误;
C、四个角相等的菱形是正方形,故原命题正确;
D、两条对角线相等的平行四边形是矩形,故原命题错误,
故选:C.
【点睛】本题考查了命题与定理的知识,解题的关键是了解特殊的平行四边形的判定方法,难度不大.
11.C
【分析】根据三角形中位线定理和直角三角形的性质可DE=AC,FH=AC,最后运用等量代换即可解答.
【详解】解:∵ D,E分别是AB,BC的中点,
∴DE=AC,
∵F为AC的中点,是的高
∴FH=AC
∴DE=FH.
故选:C.
【点睛】本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线等于第三边的一半是解答本题的关键.
12.A
【分析】根据菱形的判定逐项分析即可.
【详解】解:A. 不能使成为菱形,符合题意;
B.根据一组邻边相等的平行四边形是菱形可得是菱形,故不符合题意;
C. 根据对角线互相垂直的平行四边形是菱形可得是菱形,故不符合题意;
D. 根据对角线互相垂直的平行四边形是菱形可得是菱形,故不符合题意,
故选A.
【点睛】本题考查了菱形的判定定理,注意:菱形的判定定理有:①有一组邻边相等的平行四边形是菱形,②四条边都相等的四边形是菱形,③对角线互相垂直的平行四边形是菱形,④对角线平分一组对角的平行四边形是菱形.
13.59°
【分析】根据折叠的性质,得到,再根据平行线的性质得到,求出解决即可.
【详解】解:∵把一张长方形纸片ABCD沿EF折叠
则
故答案是59°.
【点睛】本题考查了折叠的性质以及平行线的性质,解决本题的关键是熟练掌握折叠与平行线的性质,找到相等的角.
14.5
【分析】根据折叠的性质可得,则,勾股定理求得,证明,即可求得.
【详解】解:∵,,,,
∴四边形是矩形,
,
将四边形纸片ABCD沿AE折叠,点C、D分别落在点、处,
,
,
,
中,
,
,
又
故答案为:5
【点睛】本题考查了折叠的性质,矩形的判定,勾股定理,全等三角形的性质与判定,掌握折叠的性质与勾股定理是解题的关键.
15.(答案不唯一)
【分析】本题考查正方形的判定,解题的关键是掌握:有一组邻边相等或对角线互相垂直的矩形是正方形.据此解答即可.
【详解】解:.
理由:∵四边形是矩形,
又∵,
∴四边形是正方形.
故答案为:(答案不唯一).
16.
【分析】先证四边形是平行四边形,再证,即可得出结论.本题考查矩形的判定、平行四边形的判定与性质、等知识,熟练掌握菱矩形的判定和平行四边形的判定与性质.
【详解】证明:,,
四边形是平行四边形,,
当时
∴四边形是矩形
∴当满足条件时,四边形是矩形
故答案为:
17.
【分析】根据正方形的性质可得,,然后利用证明和全等,根据全等三角形对应角相等可得,利用证明和全等,根据全等三角形对应角相等可得,从而得到,然后求出,取的中点O,连接OF、,根据直角三角形斜边上的中线等于斜边的一半可得,利用勾股定理列式求出,然后根据三角形的三边关系可知当O、F、C三点共线时,的长度最小.
【详解】解:在正方形中,,,,
在和中,
,
∴,
∴,
在和中,
,
∴,
∴,
∴,
∵,
∴,
∴,
取的中点O,连接,
则,
在中,,
根据三角形的三边关系,,
∴当O、F、C三点共线时,的长度最小,
最小值.
故答案为:.
【点睛】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系,确定出CF最小时点F的位置是解题关键,也是本题的难点.
18.(1)点B的坐标为;(2)直线的解析式为.
【分析】(1)由正方形的性质可以得到对角线之间的关系,进而得到坐标;
(2)已知两点坐标,用待定系数法求直线解析式.
【详解】解:(1)如图,连接,过点B作轴,点E为垂足,
∵四边形是正方形,
∴,,
故点B的坐标为;
(2)设直线的解析式为,
则,解得.
故直线的解析式为.
【点睛】本题考查了正方形的性质、坐标的表示、待定系数法求一次函数解析式,难度不大.
19.(1)详见解析;(2)=;(3)成立,理由详见解析.
【分析】(1)由四边形ABCD是矩形,可得AB=DC,∠ABC=∠DCB=90°,又由PB=PC可得∠PBC=∠PCB,求出∠PBA=∠PCD,进而利用SAS证明△APB≌△DPC即可得到PA=PD;
(2)当P是矩形边AD(或BC)上的一点,通过HL可证Rt△APB≌Rt△DPC,得到PA=PD;
(3)当点P在矩形ABCD内部时,同(1)可证△APB≌△DPC,得到PA=PD.
【详解】(1)证明:如图①,
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,,
∴△APB≌△DPC,
∴PA=PD;
(2) 如图②,当P是矩形边AD上的一点,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,PB=PC,
∴Rt△APB≌Rt△DPC(HL),
∴PA=PD,
当P是矩形边BC上的一点,同理可得:PA=PD,
∴若P是矩形边AD(或BC)上的一点,则PA=PD;
(3)成立.
理由如下:
如图③,
∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
∵PB=PC,
∴∠PBC=∠PCB,
∴∠PBA=∠PCD.
在△APB和△DPC中,,
∴△APB≌△DPC,
∴PA=PD.
【点睛】此题考查了矩形的性质以及全等三角形的判定和性质,难度适中,根据矩形的性质得到判定全等的条件是解决问题的关键.
20.是直角三角形,且.
【分析】设正方形的边长为x,得到,,.
然后分别利用勾股定理求出,最后得到,即可解答.
【详解】是直角三角形,理由如下:
设正方形的边长为x.
因为点是边的中点,所以.
又因为,所以,.
在中,根据勾股定理,
得.
在中,根据勾股定理,
得.
在中,根据勾股定理,
得.
因为,
所以为直角三角形,且.
【点睛】此题考查勾股定理的逆定理,正方形的性质,解题关键在于列出方程.
21.(1)
(2),证明见解析
(3)①当时,点在点处;②存在,
【分析】(1)根据勾股定理即可求出;
(2)连接,通过证明为等边三角形,即可求解;
(3)①先求出时,点Q所走路程,即可得出点Q的位置;②根据菱形的性质可得,,求出点P和点Q运动的时间,若相等,则存在,否则,不存在.
【详解】(1)解:∵四边形为矩形,
∴,
∵,,
∴;
(2)猜测:,
证明:连接,
∵为折痕,
∴垂直平分,
∴,
∵由折叠所得,
∴,
∴,则为等边三角形,
∴,
∴;
(3)解:①当时,点Q所走路程为:;
∵,
∴当时,点在点处.
②存在,
∵四边形是菱形,,
∴,
∴点Q所走路程为:;点P所走路程为;
∴点Q行走的时间(秒),点P行走的时间(秒),
∵点Q行走的时间=点P行走的时间,
∴存在,当时,四边形是菱形.
【点睛】本题主要考查了勾股定理,等边三角形的判定和性质,菱形的判定和性质,解题的关键是掌握直角三角形两直角边平方和等于斜边的平方,等边三角形三个内角都是,菱形是四条边都相等.
22.见解析
【详解】已知:四边形ABCD是矩形,AC与BD是对角线,
求证:AC=BD.
证明: ∵四边形ABCD是矩形,
∴AB=DC,∠ABC=∠DCB=90°,
又∵BC=CB,
∴△ABC≌△DCB,
∴AC=BD.
所以矩形的对角线相等.
23.(1)证明见解析;(2)证明见解析.
【分析】(1)由已知条件易证△OBC是等腰三角形,E是OC的中点,根据等腰三角形中底边上的高与中线合一的性质知BE⊥AC.
(2)利用直角三角形中斜边上的中线等于斜边的一半及中位线定理可证EG=EF.
【详解】解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,BD=2BO.
由已知BD="2AD,"
∴BO=BC.
又E是OC中点,
∴BE⊥AC.
(2)由(1)BE⊥AC,又G是AB中点,
∴EG是Rt△ABE斜边上的中线.
∴EG=AB
又∵EF是△OCD的中位线,
∴EF=CD.
又AB="CD,"
∴EG=EF.
【点睛】本题考查1.三角形中位线定理;2.等腰三角形的判定与性质;3.直角三角形斜边上的中线;4.平行四边形的性质.
24.(1)NE=2.5;
(2)NG=;
(3)AM=0.5.
【分析】(1)由折叠性质可得EN=BN,由题意可得CE=DE,在Rt△CEN中,利用勾股定理求解即可;
(2)利用正方形面积减去△ABN,△ADE和△CEN的面积可得△AEN的面积,利用勾股定理可得AE,利用三角形面积公式即可求解;
(3)连接BM,EM,由折叠性质可得AM=FM,AB=EF,∠BAD=∠EFM,可证得△ABM≌△FEM,从而得到BM=EM,在Rt△ABM和Rt△DEM中,设AM=x,则DM=4-x,利用勾股定理分别表示出BM,EM,利用等量关系构造方程即可求解.
【详解】(1)解:∵四边形ABCD为正方形,
∴∠C=90°,
∵,BC=CD=4,
∴CE=DE=2,
由折叠性质可得:EN=BN,
设EN=x,则BN=x,
∴CN=BC-BN=4-x,
在Rt△CEN中,由勾股定理可得:NE2=CN2+CE2,
即x2=(4-x)2+22,
解得:x=2.5,
∴NE=2.5;
(2)解:在Rt△ADE中,由勾股定理可得:
AE= ,
由(1)可得NE=2.5,
∴BN=2.5,
∴CN=BC-BN=1.5,
∵S ABCD=BC×CD=16,S△ABN=×AB×BN=×4×2.5=5,
S△CEN=×CN×CE=×1.5×2=1.5,S△ADE=×AD×DE=×4×2=4,
∴S△AEN=S ABCD-S△ABN-S△CEN-S△ADE=16-5-1.5-4=5.5,
∵NG⊥AE,
∴S△AEN=×AE×NG,
即5.5=×2×NG,
∴NG=;
(3)解:如图,连接BM,EM,
由折叠性质可得:
AM=FM,AB=EF,∠BAM=∠EFM,
∴△ABM≌△FEM(SAS),
∴BM=EM,
设AM=x,则DM=4-x,
在Rt△ABM中,由勾股定理可得:
BM2=AB2+AM2,即BM2=42+x2,
在Rt△DEM中,由勾股定理可得:
EM2=DM2+DE2,即EM2=(4-x)2+22,
∵BM=EM,
∴BM2=EM2,
∴42+x2=(4-x)2+22,
解得:x=0.5,
∴AM=0.5.
【点睛】本题考查折叠的性质,正方形的性质,勾股定理等知识点,解题的关键是明确折叠的性质:折叠是一种对称变换,属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
