5.1圆同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
5.1圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校计划在校园内修建一座周长为12米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是( )
A.正三角形 B.正方形 C.圆 D.不能确定
2.有下列四种说法:
①半径确定了,圆就确定了;②直径是弦;
③弦是直径;④半圆是弧,但弧不一定是半圆.
其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
3.下列作图语句描述正确的是( )
A.作射线AB,使AB=a B.作∠AOB=∠α
C.以点O为圆心作弧 D.延长直线AB到C,使AC=BC
4.下列说法:①长度相等的弧是等弧;②圆周角的度数等于圆心角度数的一半③劣弧一定比优弧短;④直径是圆中最长的弦;⑤经过三点可以作一个圆.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的有( )
A.圆中最长的弦是直径 B.弦是直径 C.弧是半圆 D.圆只有一条对称轴
6.下列命题中,属于假命题的是( )
A.三角形的内角和等于180°; B.圆是轴对称图形,任何一条直径都是圆的对称轴;
C.对顶角相等; D.在同一平面内,垂直于同一条直线的两条直线相互平行.
7.若⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
8.的半径为,点A在外,则的长可以是( )
A. B. C. D.
9.已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
A.点A在⊙O B.点A在⊙O内 C.点A在⊙O外 D.点A与圆心O重合
10.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部
B.一定在⊙O的外部
C.一定在⊙O的上
D.不能确定
11.已知点C为线段AB延长线上的一点,以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为( )
A.点B在⊙A上 B.点B在⊙A外 C.点B在⊙A内 D.不能确定
12.在中,,,,点D是AB上的中点,以点C为圆心,6为半径作圆,则点D与的位置关系是( )
A.点D在内 B.点D在上 C.点D在外 D.不能确定
二、填空题
13.一个圆的直径是4cm,周长是 cm.
14.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的 倍.(精确到个位)
15.的圆心是原点,半径为,点在上,如果点在第一象限内,那么 .
16.如图,在中,,,点是上一点,且,点是边上一动点,连接,将沿翻折得到,点与点对应,连接,则的最小值为 .
17.在同一平面内,的半径是8,点不在上,若点到上的点的最小距离是,则点到上的点最大距离是 .
三、解答题
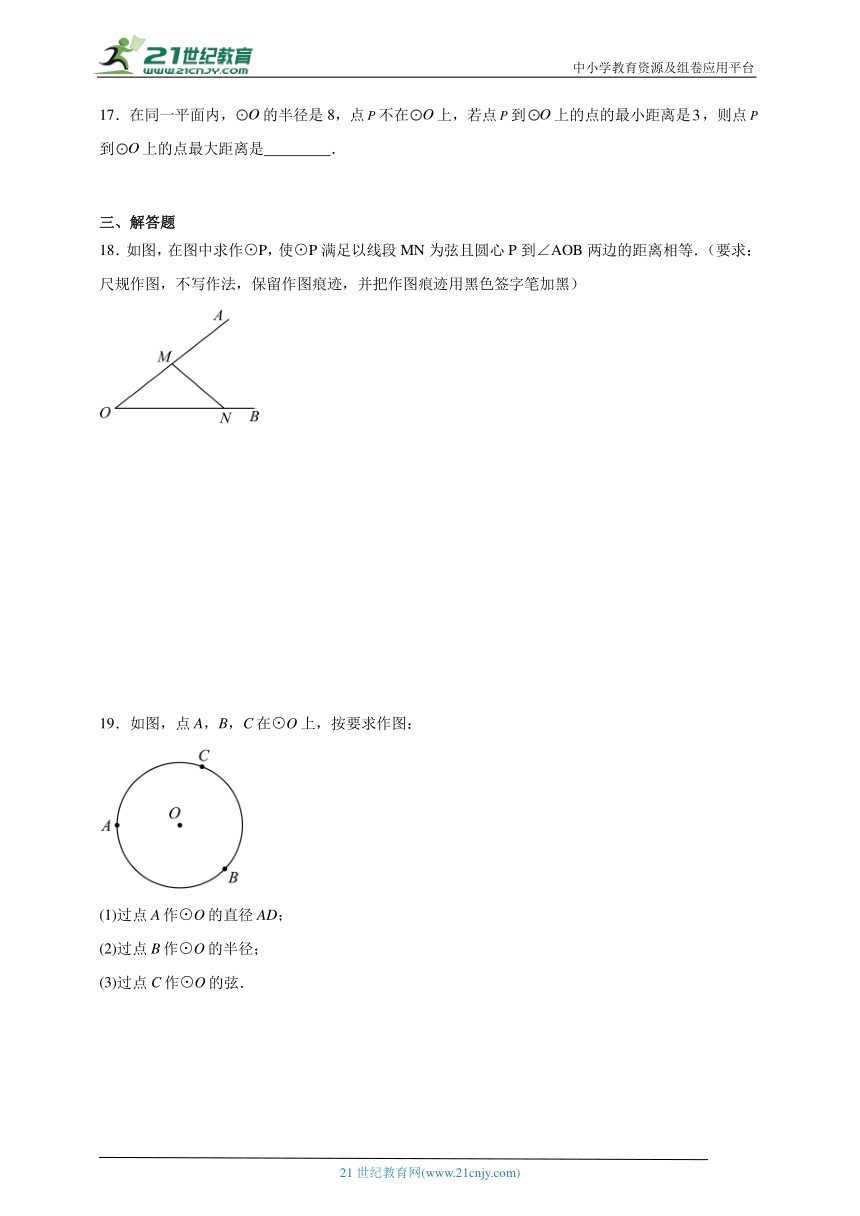
18.如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
19.如图,点A,B,C在⊙O上,按要求作图:
(1)过点A作⊙O的直径AD;
(2)过点B作⊙O的半径;
(3)过点C作⊙O的弦.
20.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
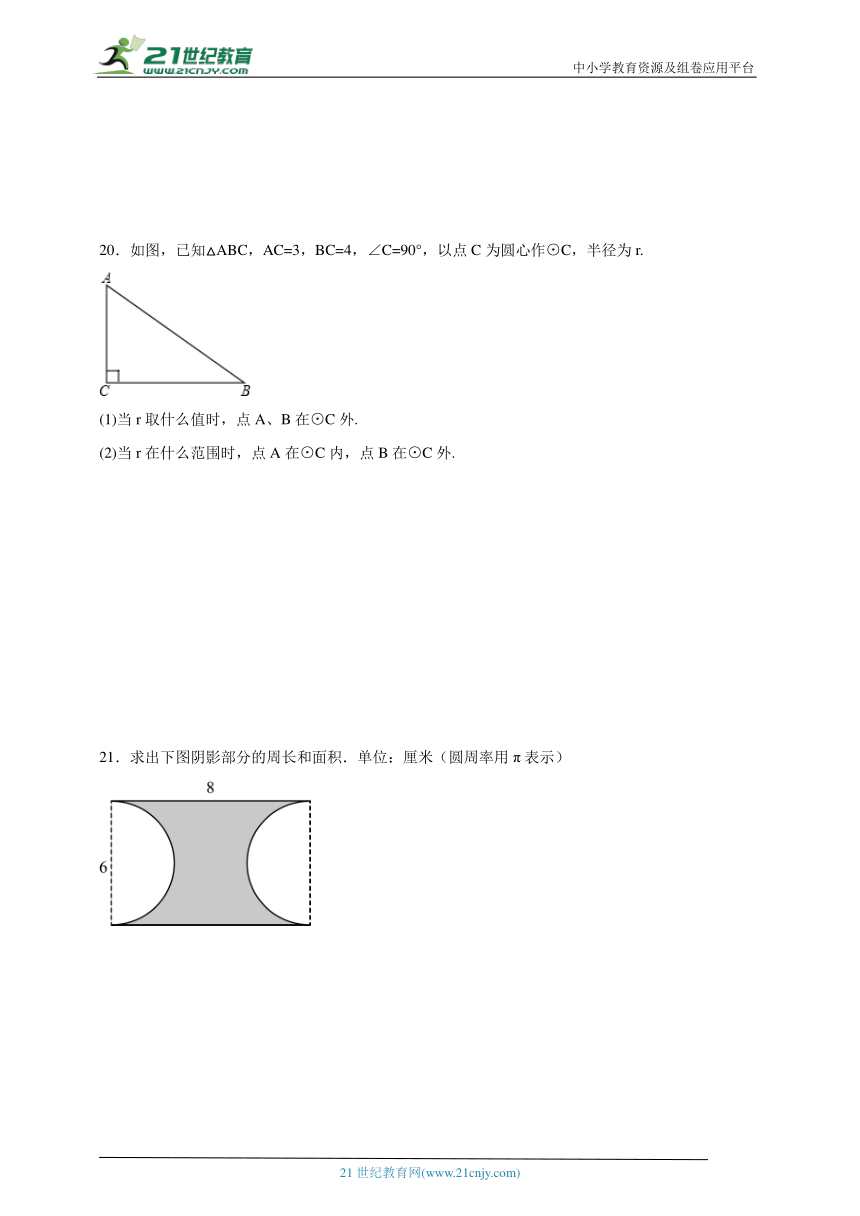
21.求出下图阴影部分的周长和面积.单位:厘米(圆周率用π表示)
22.阅读下列材料:
平面上两点P1(x1,y1),P2(x2,y2)之间的距离表示为,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为,变形可得:(x﹣a)2+(y﹣b)2=r2,我们称其为圆心为C(a,b),半径为r的圆的标准方程.例如:由圆的标准方程(x﹣1)2+(y﹣2)2=25可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.
(1)圆心为C(3,4),半径为2的圆的标准方程为: ;
(2)若已知⊙C的标准方程为:(x﹣2)2+y2=22,圆心为C,请判断点A(3,﹣1)与⊙C的位置关系.
23.⊙O的半径r=5 cm,圆心O到直线l的距离OD=3 cm,在直线l上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R三点与⊙O的位置关系各是怎样的?
24.如图,菱形的对角线相交于点O,四条边的中点分别为.这四个点共圆吗?圆心在哪里?
《5.1圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B A A B A D C B
题号 11 12
答案 C A
1.C
【分析】根据周长分别求得正三角形,正方形,圆的面积,从而比较可得到面积最大的是什么形状.
【详解】当设计成正三角形,则边长是4米,则面积是 平方米;
当设计成正方形时,边长是3米,则面积是9平方米;
当设计成圆时,半径是米,则面积是π( 平方米.
∵这三个数中最大,
∴使花坛面积最大的图案是圆.
故选C.
【点睛】本题考查了正三角形,正方形,圆的有关计算,关键是掌握面积周长一定的所有平面图形中,圆的面积最大.
2.B
【分析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.
【详解】解:圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选B.
【点睛】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.
3.B
【分析】根据射线、直线的延伸性以及确定弧的条件即可作出判断.
【详解】解:A、射线是不可度量的,故选项错误;
B、描述一个行为且角的表示正确,正确;
C、需要说明半径的长,故选项错误.
D、直线是向两方无线延伸的,故选项错误;
故选:B.
【点睛】本题考查尺规作图的定义,正确根据题意判断能否画出固定图形进而判断是解题关键.
4.A
【分析】利用圆的有关定义及确定圆的条件分别判断后即可确定正确的选项.
【详解】解:①长度相等的弧是不一定是等弧,故错误,不符合题意;
②同弧所对的圆周角的度数等于圆心角度数的一半,故原命题错误,不符合题意;
③劣弧不一定比优弧短,故原命题错误,不符合题意;
④直径是圆中最长的弦,正确,符合题意;
⑤经过不在同一直线上的三点可以作一个圆,故原命题错误,不符合题意,
正确的有1个,
故选:A.
【点睛】本题考查了圆的有关定义及确定圆的条件,解题的关键是了解圆的基础知识,难度较小.
5.A
【分析】利用圆的有关概念及性质分别判断后即可确定正确的选项.
【详解】解:A、圆中最长的弦是直径,正确,符合题意;
B、直径是弦,但弦不一定是直径,故错误,不符合题意;
C、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
D、圆有无数条对称轴,故错误,不符合题意,
故选:A.
【点睛】本题考查了圆的认识,解题的关键是正确的了解有关概念及性质,难度不大.
6.B
【分析】根据三角形内角和定理对A进行判断;根据对顶角的性质对C进行判断;根据对称轴的定义对B进行判断;根据平行线的判定方法对D进行判断.
【详解】三角形的内角和等于180°,所以A选项为真命题;
B、圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴,所以C选项为假命题;
C、对顶角相等,所以B选项为真命题;
D、在同一平面内,垂直于同一条直线的两条直线相互平行,所以D选项为真命题.
所以B选项是正确的.
【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
7.A
【详解】点在圆内,点到圆心的距离小于半径,
又因为圆的半径为6,
所以OP的长小于6,
因为5<6,所以选项A符合题意,
故选A
8.D
【分析】本题主要考查点与圆心之间的距离关系,熟练掌握点与圆心之间的距离关系是解题的关键.设点与圆心的距离为,已知点在圆外,则,即可判断.
【详解】解:当点A在外时,;
A、B、C选项均不符合;
故选:D.
9.C
【分析】根据点与圆的位置关系判断即可
【详解】∵O的半径是5,点A到圆心O的距离是7,
即点A到圆心O的距离大于圆的半径,
∴点A在O外.
故选C.
【点睛】掌握点与圆的位置关系的判定方法是解题关键.
10.B
【详解】试题分析:的直径为10,半径为5,点到点的距离大于8,点一定在的外部,故选B.
考点:点与圆的位置关系.
11.C
【分析】根据题意确定AC>AB,从而确定点与圆的位置关系即可.
【详解】解:∵点C为线段AB延长线上的一点,
∴AC>AB,
∴以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为点B在⊙A内,
故选:C.
【点睛】本题考查的知识点是点与圆的位置关系,根据题意确定出AC>AB是解此题的关键.
12.A
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,本题可由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【详解】解:由勾股定理,得
AB==10,
∵CD是AB边上的中线,
∴CD=AB=5,
∴CD=5<⊙C的半径,
∴点D在⊙C内.
故选:A.
【点睛】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
13.
【分析】根据圆的周长公式(,其中为圆的周长,为圆的直径)即可得.
【详解】圆的直径是,
圆的周长是,
故答案为:.
【点睛】本题考查了圆的周长公式,熟记公式是解题关键.
14.14
【分析】根据圆的性质和正方形的性质求圆的半径和正方形的边长,利用面积公式求解即可.
【详解】解:如图
由题意得AC与EF共线
∵圆的直径与正方形的对角线之比为3:1
∴EF:AC=3:1
∴OE:OA=3:1
设OE=3x,OA= x
在正方形ABCD中
由勾股定理得:AD=x
∴圆的面积为:π×(3x)2=9πx2
正方形的面积为(x)2=2 x2
∴9πx2÷2 x2=≈14
故答案为:14
【点睛】本题主要考查了圆的性质和正方形的性质,以及圆与正方形的面积公式的求解.
15.
【分析】如图,可得,,运用勾股定理可以求得的长,即为的值.
【详解】解:如图
由题意得:,
由勾股定理可得:,
即.
故答案为:.
【点睛】本题考查了圆的性质和勾股定理,其中根据题意画出图形确定相应线段的长是解答本题的关键.
16..
【分析】如图,作辅助圆;根据勾股定理依次求出AE、EM、AM、DM的长度,即可解决问题.
【详解】解:如图,由题意的:,
∴点在以为圆心,为半径的圆上,作;连接交于点,此时值最小;过作与.
∵,
∴,
由勾股定理得:.
∵,
∴,
∴.
∵,
∴如图中,
即线段长的最小值是.
故答案为:.
【点睛】该题主要考查了翻折变换的性质、勾股定理、最值问题等几何知识点及其应用问题;解题的关键是作辅助圆,从整体上把握题意,准确找出图形中数量关系.
17.13或19
【分析】本题考查了点与圆的位置关系.熟练掌握点与圆的位置关系是解题的关键.
由题意知,分点在内,点在外两种情况求解即可.
【详解】解:由题意知,分点在内,点在外两种情况求解;
当点在内,如图1,
∴,,
∴,
∴最大距离是13;
当点在外,如图2,
∴,,
∴,
∴最大距离是19;
综上所述,的半径是13或19;
故答案为:13或19.
18.见解析.
【详解】试题分析:先做出∠AOB的角平分线,再求出线段MN的垂直平分线就得到点P.
试题解析:
考点:尺规作图角平分线和线段的垂直平分线、圆的性质.
19.(1)见解析
(2)见解析
(3)见解析
【分析】(1)作射线,交于点,则线段即为的直径;
(2)连接,线段即为所求;
(3)连接,线段即为所求(答案不唯一).
【详解】(1)如图所示,作射线,交于点,则线段即为的直径;
(2)如图所示,连接,线段即为所求;
(3)如图所示,连接,线段即为所求的一条弦(答案不唯一).
【点睛】本题考查了圆的基本概念,连接圆上任意两点是圆的弦,直径是经过圆心的弦,半径是圆上一点与圆心的连线,掌握以上知识是解题的关键.
20.(1)0<r<3;(2)3<r<4.
【详解】试题分析:(1)要保证点在圆外,则点到圆心的距离应大于圆的半径,根据这一数量关系就可得到r的取值范围;
(2)根据点到圆心的距离小于圆的半径,则点在圆内和点到圆心的距离应大于圆的半径,则点在圆外求得r的取值范围.
试题解析:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
考点:点与圆的位置关系.
21.阴影部分的周长为(6π+16)厘米,面积为(48-9π)平方厘米
【分析】根据阴影部分的周长=一个圆的周长+矩形长的2倍,阴影部分的面积=矩形的面积﹣一个圆面积计算即可.
【详解】解:由题意知,周长=π×6+2×8=6π+16(厘米);
面积=8×6﹣π×=48﹣9π(平方厘米),
答:阴影部分的周长为(6π+16)厘米,面积为(48-9π)平方厘米.
【点睛】本题主要考查圆的周长和面积公式,熟练掌握圆的周长和面积公式是解题的关键.
22.(1);(2)点A在⊙C的内部.
【分析】(1)先设圆上任意一点的坐标(x,y),根据圆的标准方程公式求解即可;
(2)先根据圆的标准方程求出圆心坐标,利用两点距离公式求出点A到圆心的距离d,然后与半径r相比较,d>r,点在圆外,d=r,点在圆上,d<r,点在圆内,即可判断点A与圆的位置关系.
【详解】解:(1)设圆上任意一点的坐标为(x,y),
∴,
故答案为;
(2)∵⊙C的标准方程为:(x﹣2)2+y2=22,
∴圆心坐标为C(2,0),
∵点A(3,﹣1),AC=
∴点A在⊙C的内部.
【点睛】本题考查两点距离公式的拓展内容,圆的标准方程,正确理解题意、熟练掌握基本知识是解题关键.
23.点P在⊙O上;点Q在⊙O外;点R在⊙O内.
【分析】连接OR、OP、OQ,根据勾股定理求得OR、OP、OQ的长,再与半径比较即可解答.
【详解】如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,∴OP===5(cm)=r,
∴点P在⊙O上;
∵QD=5 cm,∴OQ=== (cm)>5 cm=r,
∴点Q在⊙O外;∵RD=3 cm,
∴OR===3 (cm)<5 cm=r,
∴点R在⊙O内.
【点睛】本题考查了点与圆的位置关系,解决本题的关键是首先根据勾股定理算出点到圆心的距离,再比较点到圆心的距离与圆半径大小关系完成判定.
24.共圆,圆心在点O处
【分析】根据三角形中位线的性质,证出四边形EFGH是平行四边形,根据菱形性质证出四边形EFGH是矩形,根据矩形性质可得E,F,G,H到矩形中心的距离相等,从而得出结论.
【详解】解:点E,F,G,H四点共圆,圆心在点O处. 理由如下:
连接HE,EF,FG,GH,OH,OE,OF,OG.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EF平行且等于AC, HG平行且等于AC,
∴EF平行且等于GH
∴四边形EFGH是平行四边形,
又∵四边形ABCD是菱形
∴
∴∠AOB=90°
∠HEF=90°,
∴四边形EFGH是矩形,
∴E,F,G,H到矩形中心的距离相等
∴这个矩形的四个顶点在同一个圆上,圆心即为点O.
【点睛】考核知识点:点和圆的位置关系.理解矩形、菱形的判定和性质和点和圆的位置关系是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.1圆
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校计划在校园内修建一座周长为12米的花坛,同学们设计出正三角形、正方形和圆共三种图案,其中使花坛面积最大的图案是( )
A.正三角形 B.正方形 C.圆 D.不能确定
2.有下列四种说法:
①半径确定了,圆就确定了;②直径是弦;
③弦是直径;④半圆是弧,但弧不一定是半圆.
其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
3.下列作图语句描述正确的是( )
A.作射线AB,使AB=a B.作∠AOB=∠α
C.以点O为圆心作弧 D.延长直线AB到C,使AC=BC
4.下列说法:①长度相等的弧是等弧;②圆周角的度数等于圆心角度数的一半③劣弧一定比优弧短;④直径是圆中最长的弦;⑤经过三点可以作一个圆.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的有( )
A.圆中最长的弦是直径 B.弦是直径 C.弧是半圆 D.圆只有一条对称轴
6.下列命题中,属于假命题的是( )
A.三角形的内角和等于180°; B.圆是轴对称图形,任何一条直径都是圆的对称轴;
C.对顶角相等; D.在同一平面内,垂直于同一条直线的两条直线相互平行.
7.若⊙O的半径为6,点P在⊙O内,则OP的长可能是( )
A.5 B.6 C.7 D.8
8.的半径为,点A在外,则的长可以是( )
A. B. C. D.
9.已知⊙O的半径是5,点A到圆心O的距离是7,则点A与⊙O的位置关系是( )
A.点A在⊙O B.点A在⊙O内 C.点A在⊙O外 D.点A与圆心O重合
10.已知⊙O的直径为10,点P到点O的距离大于8,那么点P的位置( )
A.一定在⊙O的内部
B.一定在⊙O的外部
C.一定在⊙O的上
D.不能确定
11.已知点C为线段AB延长线上的一点,以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为( )
A.点B在⊙A上 B.点B在⊙A外 C.点B在⊙A内 D.不能确定
12.在中,,,,点D是AB上的中点,以点C为圆心,6为半径作圆,则点D与的位置关系是( )
A.点D在内 B.点D在上 C.点D在外 D.不能确定
二、填空题
13.一个圆的直径是4cm,周长是 cm.
14.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的 倍.(精确到个位)
15.的圆心是原点,半径为,点在上,如果点在第一象限内,那么 .
16.如图,在中,,,点是上一点,且,点是边上一动点,连接,将沿翻折得到,点与点对应,连接,则的最小值为 .
17.在同一平面内,的半径是8,点不在上,若点到上的点的最小距离是,则点到上的点最大距离是 .
三、解答题
18.如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
19.如图,点A,B,C在⊙O上,按要求作图:
(1)过点A作⊙O的直径AD;
(2)过点B作⊙O的半径;
(3)过点C作⊙O的弦.
20.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
21.求出下图阴影部分的周长和面积.单位:厘米(圆周率用π表示)
22.阅读下列材料:
平面上两点P1(x1,y1),P2(x2,y2)之间的距离表示为,称为平面内两点间的距离公式,根据该公式,如图,设P(x,y)是圆心坐标为C(a,b)、半径为r的圆上任意一点,则点P适合的条件可表示为,变形可得:(x﹣a)2+(y﹣b)2=r2,我们称其为圆心为C(a,b),半径为r的圆的标准方程.例如:由圆的标准方程(x﹣1)2+(y﹣2)2=25可得它的圆心为(1,2),半径为5.根据上述材料,结合你所学的知识,完成下列各题.
(1)圆心为C(3,4),半径为2的圆的标准方程为: ;
(2)若已知⊙C的标准方程为:(x﹣2)2+y2=22,圆心为C,请判断点A(3,﹣1)与⊙C的位置关系.
23.⊙O的半径r=5 cm,圆心O到直线l的距离OD=3 cm,在直线l上有P,Q,R三点,且有PD=4 cm,QD=5 cm,RD=3 cm,那么P,Q,R三点与⊙O的位置关系各是怎样的?
24.如图,菱形的对角线相交于点O,四条边的中点分别为.这四个点共圆吗?圆心在哪里?
《5.1圆》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B B A A B A D C B
题号 11 12
答案 C A
1.C
【分析】根据周长分别求得正三角形,正方形,圆的面积,从而比较可得到面积最大的是什么形状.
【详解】当设计成正三角形,则边长是4米,则面积是 平方米;
当设计成正方形时,边长是3米,则面积是9平方米;
当设计成圆时,半径是米,则面积是π( 平方米.
∵这三个数中最大,
∴使花坛面积最大的图案是圆.
故选C.
【点睛】本题考查了正三角形,正方形,圆的有关计算,关键是掌握面积周长一定的所有平面图形中,圆的面积最大.
2.B
【分析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.
【详解】解:圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.
其中错误说法的是①③两个.
故选B.
【点睛】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.
3.B
【分析】根据射线、直线的延伸性以及确定弧的条件即可作出判断.
【详解】解:A、射线是不可度量的,故选项错误;
B、描述一个行为且角的表示正确,正确;
C、需要说明半径的长,故选项错误.
D、直线是向两方无线延伸的,故选项错误;
故选:B.
【点睛】本题考查尺规作图的定义,正确根据题意判断能否画出固定图形进而判断是解题关键.
4.A
【分析】利用圆的有关定义及确定圆的条件分别判断后即可确定正确的选项.
【详解】解:①长度相等的弧是不一定是等弧,故错误,不符合题意;
②同弧所对的圆周角的度数等于圆心角度数的一半,故原命题错误,不符合题意;
③劣弧不一定比优弧短,故原命题错误,不符合题意;
④直径是圆中最长的弦,正确,符合题意;
⑤经过不在同一直线上的三点可以作一个圆,故原命题错误,不符合题意,
正确的有1个,
故选:A.
【点睛】本题考查了圆的有关定义及确定圆的条件,解题的关键是了解圆的基础知识,难度较小.
5.A
【分析】利用圆的有关概念及性质分别判断后即可确定正确的选项.
【详解】解:A、圆中最长的弦是直径,正确,符合题意;
B、直径是弦,但弦不一定是直径,故错误,不符合题意;
C、半圆是弧,但弧不一定是半圆,故错误,不符合题意;
D、圆有无数条对称轴,故错误,不符合题意,
故选:A.
【点睛】本题考查了圆的认识,解题的关键是正确的了解有关概念及性质,难度不大.
6.B
【分析】根据三角形内角和定理对A进行判断;根据对顶角的性质对C进行判断;根据对称轴的定义对B进行判断;根据平行线的判定方法对D进行判断.
【详解】三角形的内角和等于180°,所以A选项为真命题;
B、圆是轴对称图形,任何一条直径所在的直线都是圆的对称轴,所以C选项为假命题;
C、对顶角相等,所以B选项为真命题;
D、在同一平面内,垂直于同一条直线的两条直线相互平行,所以D选项为真命题.
所以B选项是正确的.
【点睛】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.
7.A
【详解】点在圆内,点到圆心的距离小于半径,
又因为圆的半径为6,
所以OP的长小于6,
因为5<6,所以选项A符合题意,
故选A
8.D
【分析】本题主要考查点与圆心之间的距离关系,熟练掌握点与圆心之间的距离关系是解题的关键.设点与圆心的距离为,已知点在圆外,则,即可判断.
【详解】解:当点A在外时,;
A、B、C选项均不符合;
故选:D.
9.C
【分析】根据点与圆的位置关系判断即可
【详解】∵O的半径是5,点A到圆心O的距离是7,
即点A到圆心O的距离大于圆的半径,
∴点A在O外.
故选C.
【点睛】掌握点与圆的位置关系的判定方法是解题关键.
10.B
【详解】试题分析:的直径为10,半径为5,点到点的距离大于8,点一定在的外部,故选B.
考点:点与圆的位置关系.
11.C
【分析】根据题意确定AC>AB,从而确定点与圆的位置关系即可.
【详解】解:∵点C为线段AB延长线上的一点,
∴AC>AB,
∴以A为圆心,AC长为半径作⊙A,则点B与⊙A的位置关系为点B在⊙A内,
故选:C.
【点睛】本题考查的知识点是点与圆的位置关系,根据题意确定出AC>AB是解此题的关键.
12.A
【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系,本题可由勾股定理等性质算出点与圆心的距离d,则d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内.
【详解】解:由勾股定理,得
AB==10,
∵CD是AB边上的中线,
∴CD=AB=5,
∴CD=5<⊙C的半径,
∴点D在⊙C内.
故选:A.
【点睛】本题考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.
13.
【分析】根据圆的周长公式(,其中为圆的周长,为圆的直径)即可得.
【详解】圆的直径是,
圆的周长是,
故答案为:.
【点睛】本题考查了圆的周长公式,熟记公式是解题关键.
14.14
【分析】根据圆的性质和正方形的性质求圆的半径和正方形的边长,利用面积公式求解即可.
【详解】解:如图
由题意得AC与EF共线
∵圆的直径与正方形的对角线之比为3:1
∴EF:AC=3:1
∴OE:OA=3:1
设OE=3x,OA= x
在正方形ABCD中
由勾股定理得:AD=x
∴圆的面积为:π×(3x)2=9πx2
正方形的面积为(x)2=2 x2
∴9πx2÷2 x2=≈14
故答案为:14
【点睛】本题主要考查了圆的性质和正方形的性质,以及圆与正方形的面积公式的求解.
15.
【分析】如图,可得,,运用勾股定理可以求得的长,即为的值.
【详解】解:如图
由题意得:,
由勾股定理可得:,
即.
故答案为:.
【点睛】本题考查了圆的性质和勾股定理,其中根据题意画出图形确定相应线段的长是解答本题的关键.
16..
【分析】如图,作辅助圆;根据勾股定理依次求出AE、EM、AM、DM的长度,即可解决问题.
【详解】解:如图,由题意的:,
∴点在以为圆心,为半径的圆上,作;连接交于点,此时值最小;过作与.
∵,
∴,
由勾股定理得:.
∵,
∴,
∴.
∵,
∴如图中,
即线段长的最小值是.
故答案为:.
【点睛】该题主要考查了翻折变换的性质、勾股定理、最值问题等几何知识点及其应用问题;解题的关键是作辅助圆,从整体上把握题意,准确找出图形中数量关系.
17.13或19
【分析】本题考查了点与圆的位置关系.熟练掌握点与圆的位置关系是解题的关键.
由题意知,分点在内,点在外两种情况求解即可.
【详解】解:由题意知,分点在内,点在外两种情况求解;
当点在内,如图1,
∴,,
∴,
∴最大距离是13;
当点在外,如图2,
∴,,
∴,
∴最大距离是19;
综上所述,的半径是13或19;
故答案为:13或19.
18.见解析.
【详解】试题分析:先做出∠AOB的角平分线,再求出线段MN的垂直平分线就得到点P.
试题解析:
考点:尺规作图角平分线和线段的垂直平分线、圆的性质.
19.(1)见解析
(2)见解析
(3)见解析
【分析】(1)作射线,交于点,则线段即为的直径;
(2)连接,线段即为所求;
(3)连接,线段即为所求(答案不唯一).
【详解】(1)如图所示,作射线,交于点,则线段即为的直径;
(2)如图所示,连接,线段即为所求;
(3)如图所示,连接,线段即为所求的一条弦(答案不唯一).
【点睛】本题考查了圆的基本概念,连接圆上任意两点是圆的弦,直径是经过圆心的弦,半径是圆上一点与圆心的连线,掌握以上知识是解题的关键.
20.(1)0<r<3;(2)3<r<4.
【详解】试题分析:(1)要保证点在圆外,则点到圆心的距离应大于圆的半径,根据这一数量关系就可得到r的取值范围;
(2)根据点到圆心的距离小于圆的半径,则点在圆内和点到圆心的距离应大于圆的半径,则点在圆外求得r的取值范围.
试题解析:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
考点:点与圆的位置关系.
21.阴影部分的周长为(6π+16)厘米,面积为(48-9π)平方厘米
【分析】根据阴影部分的周长=一个圆的周长+矩形长的2倍,阴影部分的面积=矩形的面积﹣一个圆面积计算即可.
【详解】解:由题意知,周长=π×6+2×8=6π+16(厘米);
面积=8×6﹣π×=48﹣9π(平方厘米),
答:阴影部分的周长为(6π+16)厘米,面积为(48-9π)平方厘米.
【点睛】本题主要考查圆的周长和面积公式,熟练掌握圆的周长和面积公式是解题的关键.
22.(1);(2)点A在⊙C的内部.
【分析】(1)先设圆上任意一点的坐标(x,y),根据圆的标准方程公式求解即可;
(2)先根据圆的标准方程求出圆心坐标,利用两点距离公式求出点A到圆心的距离d,然后与半径r相比较,d>r,点在圆外,d=r,点在圆上,d<r,点在圆内,即可判断点A与圆的位置关系.
【详解】解:(1)设圆上任意一点的坐标为(x,y),
∴,
故答案为;
(2)∵⊙C的标准方程为:(x﹣2)2+y2=22,
∴圆心坐标为C(2,0),
∵点A(3,﹣1),AC=
∴点A在⊙C的内部.
【点睛】本题考查两点距离公式的拓展内容,圆的标准方程,正确理解题意、熟练掌握基本知识是解题关键.
23.点P在⊙O上;点Q在⊙O外;点R在⊙O内.
【分析】连接OR、OP、OQ,根据勾股定理求得OR、OP、OQ的长,再与半径比较即可解答.
【详解】如图,连接OR,OP,OQ.
∵PD=4 cm,OD=3 cm,且OD⊥l,∴OP===5(cm)=r,
∴点P在⊙O上;
∵QD=5 cm,∴OQ=== (cm)>5 cm=r,
∴点Q在⊙O外;∵RD=3 cm,
∴OR===3 (cm)<5 cm=r,
∴点R在⊙O内.
【点睛】本题考查了点与圆的位置关系,解决本题的关键是首先根据勾股定理算出点到圆心的距离,再比较点到圆心的距离与圆半径大小关系完成判定.
24.共圆,圆心在点O处
【分析】根据三角形中位线的性质,证出四边形EFGH是平行四边形,根据菱形性质证出四边形EFGH是矩形,根据矩形性质可得E,F,G,H到矩形中心的距离相等,从而得出结论.
【详解】解:点E,F,G,H四点共圆,圆心在点O处. 理由如下:
连接HE,EF,FG,GH,OH,OE,OF,OG.
∵E,F,G,H分别是AB,BC,CD,DA的中点,
∴EF平行且等于AC, HG平行且等于AC,
∴EF平行且等于GH
∴四边形EFGH是平行四边形,
又∵四边形ABCD是菱形
∴
∴∠AOB=90°
∠HEF=90°,
∴四边形EFGH是矩形,
∴E,F,G,H到矩形中心的距离相等
∴这个矩形的四个顶点在同一个圆上,圆心即为点O.
【点睛】考核知识点:点和圆的位置关系.理解矩形、菱形的判定和性质和点和圆的位置关系是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
