5.3垂径定理同步练习(含解析)
图片预览



文档简介
中小学教育资源及组卷应用平台
5.3垂径定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,⊙O的半径为10,弦AB的长度是16,ON垂直AB,垂足为N,则ON的长度为( )
A.5 B.6 C.8 D.10
2.如图工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.则这个小圆孔的宽口AB的长度是( )
A.5mm B.6mm C.8mm D.10mm
3.如图,是的直径,为弦,于点E,则下列结论中不成立的是( )
A. B. C. D.
4.如图,在中,是弦,,半径为4,.则的长( )
A. B. C. D.
5.如图,的弦交直径于E,,,则的长为( )
A. B. C. D.
6.下列语句,错误的是( )
A.直径是弦 B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心 D.平分弧的半径垂直于弧所对的弦
7.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE C.OE=CE D.∠AOC=60°
8.如图是一个圆弧形门拱,拱高,跨度,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是【 】
A.CM=DM B. C.∠ACD=∠ADC D.OM=MD
10.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8 B.2 C.2或8 D.3或7
11.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
12.如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是( )
A.若⊙O的半径是2,点E是OB的中点,则CD=
B.若CD=,则⊙O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
二、填空题
13.过⊙O内一点M的最长弦长为10cm,最短弦长8cm,那么⊙O的半径等于 ,OM的长为 .
14.如图所示,在内有折线,其中,则的长为 .
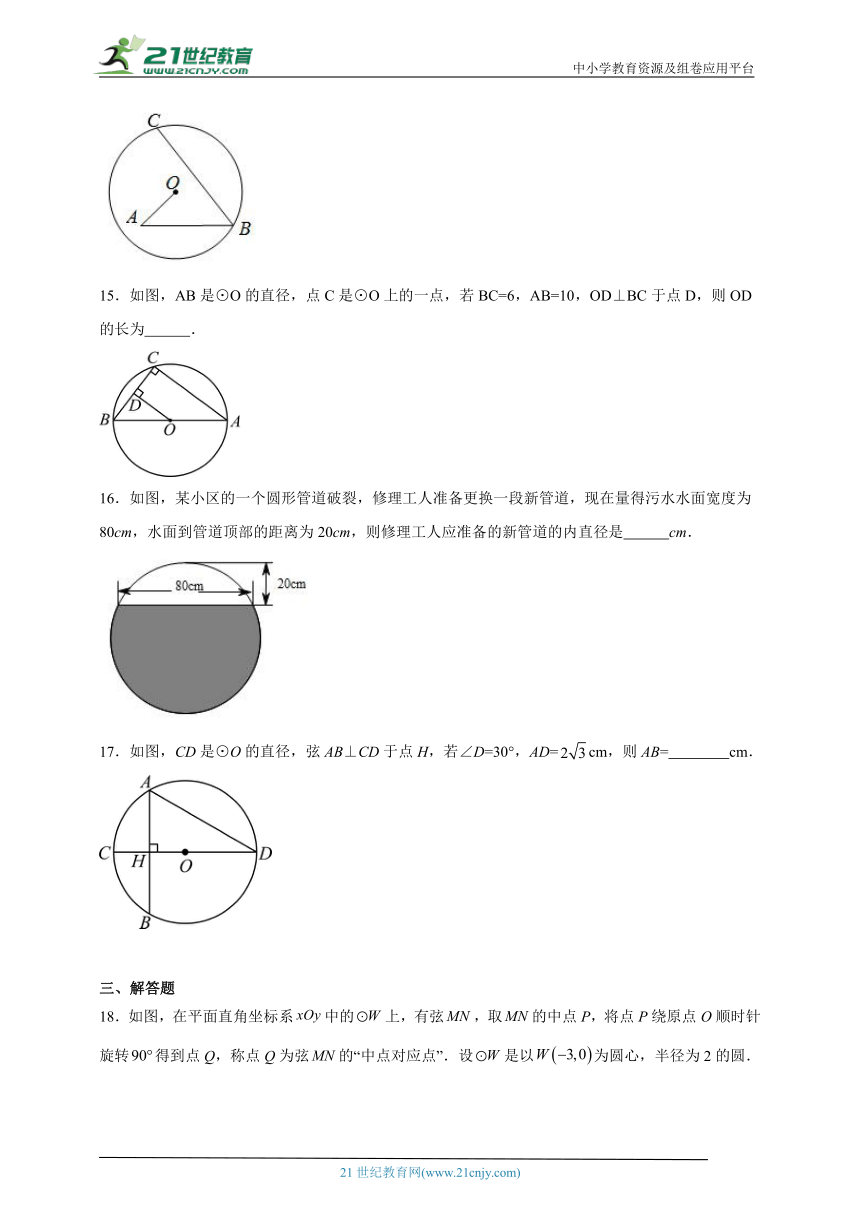
15.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
16.如图,某小区的一个圆形管道破裂,修理工人准备更换一段新管道,现在量得污水水面宽度为80cm,水面到管道顶部的距离为20cm,则修理工人应准备的新管道的内直径是 cm.
17.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,AD=cm,则AB= cm.
三、解答题
18.如图,在平面直角坐标系中的上,有弦,取的中点P,将点P绕原点O顺时针旋转得到点Q,称点Q为弦的“中点对应点”.设是以为圆心,半径为2的圆.
(1)已知弦长度为2,点Q为弦的“中点对应点”.
①当轴时,在图1中画出点Q,并且直接写出线段的长度;
②当在圆上运动时,直接写出线段的取值范围.
(2)已知点,点N为上的一动点,设直线与x轴、y轴分别交于点A、点B,若线段上存在弦的“中点对应点”点Q,求出b的取值范围.
19.在直径为的圆柱形油槽内装入一些油后,截面如图,油面宽为,当油面宽为时,油上升了多少厘米?
王源的解题步骤如下:
[解]连接,过点作于点.
于点,且为弦,.
当时,在中,.
当时,在中,.
.即油上升了.
请问王源的解题过程正确吗?如果不正确,请写出正确的解题步骤.
20.如图,是的直径,于点,连接并延长交于点,且恰为的中点.
(1)求的度数;
(2)证明:是的中点.
21.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.
(1)求OD的长.
(2)求EC的长.
22.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
23.如图,AB是⊙O的直径,点P是AB上一点,且点P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据;(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求⊙O的半径.
24.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
《5.3垂径定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D B B B D C
题号 11 12
答案 A C
1.B
【分析】根据⊙O的半径为10,弦AB的长度是16,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
【详解】解:由题意可得,
故选B.
【点睛】本题考查垂径定理,解题的关键是明确垂径定理的主要内容,利用垂径定理解答问题.
2.C
【分析】连接AB,OA,过点O作OD⊥AB于点D,先根据钢珠的直径是10mm,钢珠顶端离零件表面的距离为8mm求出OA及OD的长,再根据勾股定理即可求出AD的长,由垂径定理即可得出结论.
【详解】
解:连接AB,OA,过点O作OD⊥AB于点D,
∵钢珠的直径是10mm,钢珠顶端离零件表面的距离为8mm,
∴OA=5mm,OD=8-5=3mm,
∵OD⊥AB,
∴在Rt△OAD中,AD===4mm,
∴AB=2AD=8mm.
故选C.
【点睛】本题考查的是垂径定理在实际生活中的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
3.C
【分析】根据垂径定理可得:,,进而得到,无法得到,即可得到答案.
【详解】解:是的直径,为弦,于点E,
,,
B、D选项结论成立,不符合题意;
,
,
A选项结论成立,不符合题意;
无法判断,
C选项结论不成立,符合题意,
故选C.
【点睛】本题主要考查了垂径定理,熟练掌握垂直弦的直径平分弦,并且平分弦所对的弧是解题关键.
4.C
【分析】作于点C,连接,根据30°所对的直角边等于斜边的一半可得,根据勾股定理可得的长,再根据垂径定理可得的长.
【详解】解:如图,作于点C,连接,
∵
∴,
∴,
∴.
故选:C.
【点睛】本题考查垂径定理以及勾股定理,作出辅助线构造直角三角形是解题的关键.
5.D
【分析】过点O作于点F,先根据已知条件求出,则,再根据垂径定理得到,则,利用勾股定理求出即可求出.
【详解】解:过点O作于点F,
∵,,
∴,
∴,
∴由垂径定理可知:,
∴,
∴由勾股定理可知:,
在中,由勾股定理可知:,
故选:D.
【点睛】本题主要考查了垂径定理,勾股定理相关知识,正确作出辅助线构造直角三角形是解题的关键.
6.B
【分析】将每一句话进行分析和处理即可得出本题答案.
【详解】A.直径是弦,正确.
B.∵在同圆或等圆中,相等的圆心角所对的弧相等,
∴相等的圆心角所对的弧相等,错误.
C.弦的垂直平分线一定经过圆心,正确.
D.平分弧的半径垂直于弧所对的弦,正确.
故答案选:B.
【点睛】本题考查了圆中弦、圆心角、弧度之间的关系,熟练掌握该知识点是本题解题的关键.
7.B
【分析】根据垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧求解.
【详解】解:∵直径AB⊥弦CD
∴CE=DE
故选B.
【点睛】本题考查垂径定理,本题属于基础应用题,只需学生熟练掌握垂径定理,即可完成.
8.B
【分析】设这个门拱的半径为r,则OB=r-1,根据垂径定理求出BC的长,再根据勾股定理求出r的值即可.
【详解】设这个门拱的半径为r,则OB=r 1,
∵CD=4m,AB⊥CD,
∴BC=CD=2m,
在Rt△BOC中,
∵BC+OB=OC,即2+(r 1) =r,解得r=2.5m.
故选B.
【点睛】此题考查垂径定理的应用,勾股定理,解题关键在于求出BC的长.
9.D
【详解】∵AB是⊙O的直径,弦CD⊥AB,垂足为M,
∴M为CD的中点,即CM=DM,选项A成立;
∵B为的中点,即,选项B成立;
在△ACM和△ADM中,∵AM=AM,∠AMC=∠AMD=90°,CM=DM,
∴△ACM≌△ADM(SAS),∴∠ACD=∠ADC,选项C成立.
而OM与MD不一定相等,选项D不成立.故选D.
10.C
【详解】如图,连接OC,
∵直径AB⊥CD,
∴根据垂径定理,CE=DE=CD=×8=4.
在Rt△OCE中,OC=AB=5,
∴根据勾股定理,.
当点E在半径OB上时,BE=OB﹣OE=5﹣3=2;
当点E在半径OA上时,BE=OB+OE=5+3=8.
∴BE的长为2或8.
故选:C.
11.A
【分析】由题意可知,C、O、G三点在一条直线上OG最小,MN最大,再由勾股定理求得AB,然后由三角形面积求得CF,最后由垂径定理和勾股定理即可求得MN的最大值.
【详解】解:如图,过O作OG⊥AB于G,连接OC、OM,
∵DE=6,∠ACB=90°,OD=OE,
∴OC=DE=3,
∵OM=3,
∴只有OG最小,GM才能最大,从而MN有最大值,
∴只有C、O、G三点在一条直线上OG最小,
过C作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10,
∵AC BC=AB CF,
∴CF=,
∴OG=CF OC=,
∴MG==,
∴MN=2MG=
故选:A
【点睛】本题考查了勾股定理,垂线段最短,垂径定理等知识,正确作出辅助线,得出C、O、G三点在一条直线上OG最小是解题的关键.
12.C
【分析】根据垂径定理,解直角三角形知识,一一求解判断即可.
【详解】解:A、∵OC=OB=2,
∵点E是OB的中点,
∴OE=1,
∵CD⊥AB,
∴∠CEO=90°,CD=2CE,
∴ ,
∴,本选项错误不符合题意;
B、根据,缺少条件,无法得出半径是1,本选项错误,不符合题意;
C、∵∠A=30°,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴BC=OC,
∵CD⊥AB,
∴CE=DE,
∴BC=BD,
∴OC=OD=BC=BD,
∴四边形OCBD是菱形;故本选项正确本选项符合题意.
D、∵四边形OCBD是平行四边形,OC=OD,
所以四边形OCBD是菱形
∴OC=BC,
∵OC=OB,
∴OC=OB=BC,
∴∠BOC=60°,
∴,故本选项错误不符合题意..
故选:C.
【点睛】本题考查了圆周角定理,垂径定理,菱形的判定和性质,等边三角形的判定和性质,正确的理解题意是解题的关键.
13. 5cm 3cm
【分析】如图,过⊙O内一点M的最长的弦为直角AD,最短的弦为垂直OM的弦BC,由已知可得AD=10cm,BC=8cm,然后利用勾股定理求得OM的长即可.
【详解】
如图,过⊙O内一点M的最长的弦为直角AD,最短的弦为垂直OM的弦BC,
由已知可得AD=10cm,BC=8cm,
∴OA=OB=5cm,BM=4cm,
则OM==3cm.
故答案为5cm;3cm.
【点睛】本题主要考查了圆的基本知识点,垂径定理,解此题的关键在于熟练掌握其知识点.
14.
【分析】过点O分别作OD⊥AB,OE⊥BC,垂足分别为点D、E,延长DO交BC于点H,连接OB,然后根据含30°角的直角三角形的性质可求OD的长,进而可得BD,然后利用勾股定理及垂径定理可求解问题.
【详解】解:过点O分别作OD⊥AB,OE⊥BC,垂足分别为点D、E,延长DO交BC于点H,如图所示:
∴BE=CE,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,,
∴OH=4,
∵∠HDB=90°,
∴∠HOE=30°,
∴,
∴,
∴;
故答案为.
【点睛】本题主要考查垂径定理及含30°直角三角形的性质,熟练掌握垂径定理及含30°直角三角形的性质是解题的关键.
15.4
【分析】根据垂径定理求得BD,然后根据勾股定理求得即可.
【详解】解:∵OD⊥BC,
∴BD=CD=BC=3,
∵OB=AB=5,
∴在Rt△OBD中,OD==4.
故答案为4.
【点睛】本题考查垂径定理及其勾股定理,熟记定理并灵活应用是本题的解题关键.
16.100
【分析】由垂径定理和勾股定理计算即可.
【详解】如图所示,作管道圆心O,管道顶部为A点,污水水面为BD,连接AO,AO与BD垂直相交于点C.
设AO=OB=r
则OC=r-20,BC=
有
化简得r=50
故新管道直径为100cm.
故答案为:100.
【点睛】本题为垂径定理的实际应用题,主要是通过圆心距,圆的半径及弦长的一半构成直角三角形,并应用勾股定理,来解决问题.
17.
【分析】根据∠D=30°,直角三角形中30°角对应的直角边等于斜边的一半计算出AH,再根据垂直于弦的直径平分弦得到AB=2AH计算出AB.
【详解】在中,∠D=30°
∴
∴cm
∵弦AB⊥CD
∴cm
故答案为:
【点睛】本题考查直角三角形和圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.
18.(1)①图见解析,;②;
(2).
【分析】(1)①连接、,由题意可得,求得点的坐标,即可求解,由旋转的性质可得,利用勾股定理即可求解;②确定点的运动轨迹,即可求解;
(2)如图,在上,记与轴的交点记为,,当靠近时,为分界点,可得此时的最小值,当靠近时,如图,连接,设点,根据旋转的性质可得,弦的中点,求得点的坐标,根据,得到关于的一元二次方程,根据判别式,可得的最大值,从而即可求解.
【详解】(1)解:①连接、,如下图:
由题意可得:,,,,
由勾股定理可得:,
即,
将点P绕原点O顺时针旋转得到点Q,则点,
由旋转的性质可得:;
②由①可得,则当在圆上运动时,点的轨迹是以为圆心,以为半径的圆,
取点,连接,如下图,
由题意可得:,,,
∴
∴,
∴点的轨迹是以为圆心,以为半径的圆,
则,
则的最小值为:,最大值为,
即.
(2)解:如图,∵在上,
记与轴的交点记为,,当靠近时,为分界点,
此时,,重合,,重合,,重合,
∴过,
∴,
当靠近时,如图,连接,
由题意设点,
根据旋转的性质可得,弦的中点
又,则,
由题意可得,即,
化简可得:,
由题意可得:,
解得:,
综上.
【点睛】此题考查了圆的性质,旋转的性质,全等三角形的判定与性质,一元二次方程根与判别式的关系,解题的关键是理解题意,熟练掌握相关基础性质.
19.王源的解题过程不正确.正确解题步骤见解析.油上升了或.
【分析】连接AO,过点O作OC⊥AB于点C,根据垂径定理结合勾股定理求出当AB=6cm和8cm时OC的长度,即可得出结论.
【详解】王源的解题过程不正确.正确解题步骤如下:
连接,过点作于点,如图所示.
∵于点,且为弦,.
当时,在中,,;
当时,在中,.
或.
答:油上升了或.
【点睛】本题主要考查了垂径定理以及勾股定理,解题的关键是求出OC的长,根据OC的变化来得出结论.
20.(1)
(2)见解析
【分析】本题考查了垂径定理、等边三角形的判定与性质、线段垂直平分线的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)连接,由垂径定理得出,由线段垂直平分线的性质得出,,从而得出,推出是等边三角形,即可得出结论;
(2)证明出是等边三角形,结合得出,即可得证.
【详解】(1)解:如图,连接,
,,为的直径,
,
垂直平分,
,
为的中点,过圆心,
,
垂直平分,
,
,
是等边三角形,
,,
(2)解:为的中点,
,
,
,
为等边三角形,
,
,即是的中点.
21.(1)5 (2)
【分析】(1)设⊙O的半径为r,根据垂径定理求出AC的长,在Rt△OAC中利用勾股定理求出r的值;
(2)连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
【详解】解:(1)设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,
r=5,
∴OD=r=5;
(2)连接BE,如图:
由(1)得:AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,EC===2.
故答案为(1)5;(2).
【点睛】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
22.(1)见解析;(2) 169πcm .
【分析】(1)由垂径定理知,垂直于弦的直径是弦的中垂线,故作AC,BC的中垂线交于点O,则点O是弧ACB所在圆的圆心;
(2)在Rt△OAD中,由勾股定理可求得半径OA的长,由圆的面积公式进行计算即可.
【详解】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x 8)cm,
则根据勾股定理列方程:
x2=122+(x 8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:×132=169(cm2).
【点睛】本题考查的是垂径定理和勾股定理的应用,垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
23.(1)画图见解析,依据:平分弦(非直径)的直径垂直于弦;(2)⊙O的半径为5.
【分析】(1)过P点作AB的垂线即可,作图依据是垂径定理的推论.
(2)设⊙O的半径为r,在Rt△OPD中,利用勾股定理构建方程即可解决问题.
【详解】(1)过P点作AB的垂线交圆与C、D两点, CD就是所求的弦,如图.
依据:平分弦(非直径)的直径垂直于弦;
(2)如图,连接OD,
∵OA⊥CD于点P,AB是⊙O的直径,
∴∠OPD=90°,PD=CD,
∵CD=8,
∴PD=4.
设⊙O的半径为r,则OD=r,OP=OA﹣AP=r﹣2,
在Rt△ODP中,∠OPD=90°,
∴OD2=OP2+PD2,
即r2=(r﹣2)2+42,
解得r=5,
即⊙O的半径为5.
【点睛】本题主要考查了垂径定理,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
24.OE=OF,证明见解析.
【详解】试题分析:
过O作OM⊥AB于M,
∴AM=BM
∵AE=BF
∴EM="FM"
即OM垂直平分EF
∴OE=OF
考点:本题考查的是垂径定理,垂直平分线的性质
点评:解答本题的关键是熟练掌握垂直平分线的性质:垂直平分线上的点到线段两端的距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.3垂径定理
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图所示,⊙O的半径为10,弦AB的长度是16,ON垂直AB,垂足为N,则ON的长度为( )
A.5 B.6 C.8 D.10
2.如图工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示.则这个小圆孔的宽口AB的长度是( )
A.5mm B.6mm C.8mm D.10mm
3.如图,是的直径,为弦,于点E,则下列结论中不成立的是( )
A. B. C. D.
4.如图,在中,是弦,,半径为4,.则的长( )
A. B. C. D.
5.如图,的弦交直径于E,,,则的长为( )
A. B. C. D.
6.下列语句,错误的是( )
A.直径是弦 B.相等的圆心角所对的弧相等
C.弦的垂直平分线一定经过圆心 D.平分弧的半径垂直于弧所对的弦
7.如图,已知⊙O的直径AB⊥弦CD于点E,下列结论中一定正确的是( )
A.AE=OE B.CE=DE C.OE=CE D.∠AOC=60°
8.如图是一个圆弧形门拱,拱高,跨度,那么这个门拱的半径为( )
A.2m B.2.5m C.3m D.5m
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是【 】
A.CM=DM B. C.∠ACD=∠ADC D.OM=MD
10.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( )
A.8 B.2 C.2或8 D.3或7
11.在Rt△ ABC中,∠ C=90°,BC=6,AC=8,D、E分别是AC、BC上的一点,且DE=6, 若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B. C. D.
12.如图,AB是⊙O的直径,点E是AB上一点,过点E作CD⊥AB,交⊙O于点C,D,以下结论正确的是( )
A.若⊙O的半径是2,点E是OB的中点,则CD=
B.若CD=,则⊙O的半径是1
C.若∠CAB=30°,则四边形OCBD是菱形
D.若四边形OCBD是平行四边形,则∠CAB=60°
二、填空题
13.过⊙O内一点M的最长弦长为10cm,最短弦长8cm,那么⊙O的半径等于 ,OM的长为 .
14.如图所示,在内有折线,其中,则的长为 .
15.如图,AB是⊙O的直径,点C是⊙O上的一点,若BC=6,AB=10,OD⊥BC于点D,则OD的长为 .
16.如图,某小区的一个圆形管道破裂,修理工人准备更换一段新管道,现在量得污水水面宽度为80cm,水面到管道顶部的距离为20cm,则修理工人应准备的新管道的内直径是 cm.
17.如图,CD是⊙O的直径,弦AB⊥CD于点H,若∠D=30°,AD=cm,则AB= cm.
三、解答题
18.如图,在平面直角坐标系中的上,有弦,取的中点P,将点P绕原点O顺时针旋转得到点Q,称点Q为弦的“中点对应点”.设是以为圆心,半径为2的圆.
(1)已知弦长度为2,点Q为弦的“中点对应点”.
①当轴时,在图1中画出点Q,并且直接写出线段的长度;
②当在圆上运动时,直接写出线段的取值范围.
(2)已知点,点N为上的一动点,设直线与x轴、y轴分别交于点A、点B,若线段上存在弦的“中点对应点”点Q,求出b的取值范围.
19.在直径为的圆柱形油槽内装入一些油后,截面如图,油面宽为,当油面宽为时,油上升了多少厘米?
王源的解题步骤如下:
[解]连接,过点作于点.
于点,且为弦,.
当时,在中,.
当时,在中,.
.即油上升了.
请问王源的解题过程正确吗?如果不正确,请写出正确的解题步骤.
20.如图,是的直径,于点,连接并延长交于点,且恰为的中点.
(1)求的度数;
(2)证明:是的中点.
21.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2.
(1)求OD的长.
(2)求EC的长.
22.如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24cm,CD=8cm.
(1)求作此残片所在的圆(不写作法,保留作图痕迹).
(2)求残片所在圆的面积.
23.如图,AB是⊙O的直径,点P是AB上一点,且点P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据;(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求⊙O的半径.
24.如图所示,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且AE=BF,请你找出线段OE与OF的数量关系,并给予证明.
《5.3垂径定理》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B C C C D B B B D C
题号 11 12
答案 A C
1.B
【分析】根据⊙O的半径为10,弦AB的长度是16,ON⊥AB,可以求得AN的长,从而可以求得ON的长.
【详解】解:由题意可得,
故选B.
【点睛】本题考查垂径定理,解题的关键是明确垂径定理的主要内容,利用垂径定理解答问题.
2.C
【分析】连接AB,OA,过点O作OD⊥AB于点D,先根据钢珠的直径是10mm,钢珠顶端离零件表面的距离为8mm求出OA及OD的长,再根据勾股定理即可求出AD的长,由垂径定理即可得出结论.
【详解】
解:连接AB,OA,过点O作OD⊥AB于点D,
∵钢珠的直径是10mm,钢珠顶端离零件表面的距离为8mm,
∴OA=5mm,OD=8-5=3mm,
∵OD⊥AB,
∴在Rt△OAD中,AD===4mm,
∴AB=2AD=8mm.
故选C.
【点睛】本题考查的是垂径定理在实际生活中的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
3.C
【分析】根据垂径定理可得:,,进而得到,无法得到,即可得到答案.
【详解】解:是的直径,为弦,于点E,
,,
B、D选项结论成立,不符合题意;
,
,
A选项结论成立,不符合题意;
无法判断,
C选项结论不成立,符合题意,
故选C.
【点睛】本题主要考查了垂径定理,熟练掌握垂直弦的直径平分弦,并且平分弦所对的弧是解题关键.
4.C
【分析】作于点C,连接,根据30°所对的直角边等于斜边的一半可得,根据勾股定理可得的长,再根据垂径定理可得的长.
【详解】解:如图,作于点C,连接,
∵
∴,
∴,
∴.
故选:C.
【点睛】本题考查垂径定理以及勾股定理,作出辅助线构造直角三角形是解题的关键.
5.D
【分析】过点O作于点F,先根据已知条件求出,则,再根据垂径定理得到,则,利用勾股定理求出即可求出.
【详解】解:过点O作于点F,
∵,,
∴,
∴,
∴由垂径定理可知:,
∴,
∴由勾股定理可知:,
在中,由勾股定理可知:,
故选:D.
【点睛】本题主要考查了垂径定理,勾股定理相关知识,正确作出辅助线构造直角三角形是解题的关键.
6.B
【分析】将每一句话进行分析和处理即可得出本题答案.
【详解】A.直径是弦,正确.
B.∵在同圆或等圆中,相等的圆心角所对的弧相等,
∴相等的圆心角所对的弧相等,错误.
C.弦的垂直平分线一定经过圆心,正确.
D.平分弧的半径垂直于弧所对的弦,正确.
故答案选:B.
【点睛】本题考查了圆中弦、圆心角、弧度之间的关系,熟练掌握该知识点是本题解题的关键.
7.B
【分析】根据垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧求解.
【详解】解:∵直径AB⊥弦CD
∴CE=DE
故选B.
【点睛】本题考查垂径定理,本题属于基础应用题,只需学生熟练掌握垂径定理,即可完成.
8.B
【分析】设这个门拱的半径为r,则OB=r-1,根据垂径定理求出BC的长,再根据勾股定理求出r的值即可.
【详解】设这个门拱的半径为r,则OB=r 1,
∵CD=4m,AB⊥CD,
∴BC=CD=2m,
在Rt△BOC中,
∵BC+OB=OC,即2+(r 1) =r,解得r=2.5m.
故选B.
【点睛】此题考查垂径定理的应用,勾股定理,解题关键在于求出BC的长.
9.D
【详解】∵AB是⊙O的直径,弦CD⊥AB,垂足为M,
∴M为CD的中点,即CM=DM,选项A成立;
∵B为的中点,即,选项B成立;
在△ACM和△ADM中,∵AM=AM,∠AMC=∠AMD=90°,CM=DM,
∴△ACM≌△ADM(SAS),∴∠ACD=∠ADC,选项C成立.
而OM与MD不一定相等,选项D不成立.故选D.
10.C
【详解】如图,连接OC,
∵直径AB⊥CD,
∴根据垂径定理,CE=DE=CD=×8=4.
在Rt△OCE中,OC=AB=5,
∴根据勾股定理,.
当点E在半径OB上时,BE=OB﹣OE=5﹣3=2;
当点E在半径OA上时,BE=OB+OE=5+3=8.
∴BE的长为2或8.
故选:C.
11.A
【分析】由题意可知,C、O、G三点在一条直线上OG最小,MN最大,再由勾股定理求得AB,然后由三角形面积求得CF,最后由垂径定理和勾股定理即可求得MN的最大值.
【详解】解:如图,过O作OG⊥AB于G,连接OC、OM,
∵DE=6,∠ACB=90°,OD=OE,
∴OC=DE=3,
∵OM=3,
∴只有OG最小,GM才能最大,从而MN有最大值,
∴只有C、O、G三点在一条直线上OG最小,
过C作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠ACB=90°,BC=6,AC=8,
∴AB==10,
∵AC BC=AB CF,
∴CF=,
∴OG=CF OC=,
∴MG==,
∴MN=2MG=
故选:A
【点睛】本题考查了勾股定理,垂线段最短,垂径定理等知识,正确作出辅助线,得出C、O、G三点在一条直线上OG最小是解题的关键.
12.C
【分析】根据垂径定理,解直角三角形知识,一一求解判断即可.
【详解】解:A、∵OC=OB=2,
∵点E是OB的中点,
∴OE=1,
∵CD⊥AB,
∴∠CEO=90°,CD=2CE,
∴ ,
∴,本选项错误不符合题意;
B、根据,缺少条件,无法得出半径是1,本选项错误,不符合题意;
C、∵∠A=30°,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴BC=OC,
∵CD⊥AB,
∴CE=DE,
∴BC=BD,
∴OC=OD=BC=BD,
∴四边形OCBD是菱形;故本选项正确本选项符合题意.
D、∵四边形OCBD是平行四边形,OC=OD,
所以四边形OCBD是菱形
∴OC=BC,
∵OC=OB,
∴OC=OB=BC,
∴∠BOC=60°,
∴,故本选项错误不符合题意..
故选:C.
【点睛】本题考查了圆周角定理,垂径定理,菱形的判定和性质,等边三角形的判定和性质,正确的理解题意是解题的关键.
13. 5cm 3cm
【分析】如图,过⊙O内一点M的最长的弦为直角AD,最短的弦为垂直OM的弦BC,由已知可得AD=10cm,BC=8cm,然后利用勾股定理求得OM的长即可.
【详解】
如图,过⊙O内一点M的最长的弦为直角AD,最短的弦为垂直OM的弦BC,
由已知可得AD=10cm,BC=8cm,
∴OA=OB=5cm,BM=4cm,
则OM==3cm.
故答案为5cm;3cm.
【点睛】本题主要考查了圆的基本知识点,垂径定理,解此题的关键在于熟练掌握其知识点.
14.
【分析】过点O分别作OD⊥AB,OE⊥BC,垂足分别为点D、E,延长DO交BC于点H,连接OB,然后根据含30°角的直角三角形的性质可求OD的长,进而可得BD,然后利用勾股定理及垂径定理可求解问题.
【详解】解:过点O分别作OD⊥AB,OE⊥BC,垂足分别为点D、E,延长DO交BC于点H,如图所示:
∴BE=CE,
∵,
∴,
∴,
∴,
∵,
∴,,
∴,,
∴OH=4,
∵∠HDB=90°,
∴∠HOE=30°,
∴,
∴,
∴;
故答案为.
【点睛】本题主要考查垂径定理及含30°直角三角形的性质,熟练掌握垂径定理及含30°直角三角形的性质是解题的关键.
15.4
【分析】根据垂径定理求得BD,然后根据勾股定理求得即可.
【详解】解:∵OD⊥BC,
∴BD=CD=BC=3,
∵OB=AB=5,
∴在Rt△OBD中,OD==4.
故答案为4.
【点睛】本题考查垂径定理及其勾股定理,熟记定理并灵活应用是本题的解题关键.
16.100
【分析】由垂径定理和勾股定理计算即可.
【详解】如图所示,作管道圆心O,管道顶部为A点,污水水面为BD,连接AO,AO与BD垂直相交于点C.
设AO=OB=r
则OC=r-20,BC=
有
化简得r=50
故新管道直径为100cm.
故答案为:100.
【点睛】本题为垂径定理的实际应用题,主要是通过圆心距,圆的半径及弦长的一半构成直角三角形,并应用勾股定理,来解决问题.
17.
【分析】根据∠D=30°,直角三角形中30°角对应的直角边等于斜边的一半计算出AH,再根据垂直于弦的直径平分弦得到AB=2AH计算出AB.
【详解】在中,∠D=30°
∴
∴cm
∵弦AB⊥CD
∴cm
故答案为:
【点睛】本题考查直角三角形和圆的性质,解题的关键是熟练掌握直角三角形和圆的相关知识.
18.(1)①图见解析,;②;
(2).
【分析】(1)①连接、,由题意可得,求得点的坐标,即可求解,由旋转的性质可得,利用勾股定理即可求解;②确定点的运动轨迹,即可求解;
(2)如图,在上,记与轴的交点记为,,当靠近时,为分界点,可得此时的最小值,当靠近时,如图,连接,设点,根据旋转的性质可得,弦的中点,求得点的坐标,根据,得到关于的一元二次方程,根据判别式,可得的最大值,从而即可求解.
【详解】(1)解:①连接、,如下图:
由题意可得:,,,,
由勾股定理可得:,
即,
将点P绕原点O顺时针旋转得到点Q,则点,
由旋转的性质可得:;
②由①可得,则当在圆上运动时,点的轨迹是以为圆心,以为半径的圆,
取点,连接,如下图,
由题意可得:,,,
∴
∴,
∴点的轨迹是以为圆心,以为半径的圆,
则,
则的最小值为:,最大值为,
即.
(2)解:如图,∵在上,
记与轴的交点记为,,当靠近时,为分界点,
此时,,重合,,重合,,重合,
∴过,
∴,
当靠近时,如图,连接,
由题意设点,
根据旋转的性质可得,弦的中点
又,则,
由题意可得,即,
化简可得:,
由题意可得:,
解得:,
综上.
【点睛】此题考查了圆的性质,旋转的性质,全等三角形的判定与性质,一元二次方程根与判别式的关系,解题的关键是理解题意,熟练掌握相关基础性质.
19.王源的解题过程不正确.正确解题步骤见解析.油上升了或.
【分析】连接AO,过点O作OC⊥AB于点C,根据垂径定理结合勾股定理求出当AB=6cm和8cm时OC的长度,即可得出结论.
【详解】王源的解题过程不正确.正确解题步骤如下:
连接,过点作于点,如图所示.
∵于点,且为弦,.
当时,在中,,;
当时,在中,.
或.
答:油上升了或.
【点睛】本题主要考查了垂径定理以及勾股定理,解题的关键是求出OC的长,根据OC的变化来得出结论.
20.(1)
(2)见解析
【分析】本题考查了垂径定理、等边三角形的判定与性质、线段垂直平分线的性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)连接,由垂径定理得出,由线段垂直平分线的性质得出,,从而得出,推出是等边三角形,即可得出结论;
(2)证明出是等边三角形,结合得出,即可得证.
【详解】(1)解:如图,连接,
,,为的直径,
,
垂直平分,
,
为的中点,过圆心,
,
垂直平分,
,
,
是等边三角形,
,,
(2)解:为的中点,
,
,
,
为等边三角形,
,
,即是的中点.
21.(1)5 (2)
【分析】(1)设⊙O的半径为r,根据垂径定理求出AC的长,在Rt△OAC中利用勾股定理求出r的值;
(2)连接BE,由AE是直径,根据圆周角定理得到∠ABE=90°,利用OC是△ABE的中位线得到BE=2OC=6,然后在Rt△CBE中利用勾股定理可计算出CE.
【详解】解:(1)设⊙O半径为r,则OA=OD=r,OC=r﹣2,
∵OD⊥AB,
∴∠ACO=90°,
AC=BC=AB=4,
在Rt△ACO中,由勾股定理得:r2=42+(r﹣2)2,
r=5,
∴OD=r=5;
(2)连接BE,如图:
由(1)得:AE=2r=10,
∵AE为⊙O的直径,
∴∠ABE=90°,
由勾股定理得:BE=6,
在Rt△ECB中,EC===2.
故答案为(1)5;(2).
【点睛】本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
22.(1)见解析;(2) 169πcm .
【分析】(1)由垂径定理知,垂直于弦的直径是弦的中垂线,故作AC,BC的中垂线交于点O,则点O是弧ACB所在圆的圆心;
(2)在Rt△OAD中,由勾股定理可求得半径OA的长,由圆的面积公式进行计算即可.
【详解】解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12cm,OD=(x 8)cm,
则根据勾股定理列方程:
x2=122+(x 8)2,
解得:x=13.
即:圆的半径为13cm.
所以圆的面积为:×132=169(cm2).
【点睛】本题考查的是垂径定理和勾股定理的应用,垂径定理和勾股定理相结合,构造直角三角形,可解决计算弦长、半径、弦心距等问题.
23.(1)画图见解析,依据:平分弦(非直径)的直径垂直于弦;(2)⊙O的半径为5.
【分析】(1)过P点作AB的垂线即可,作图依据是垂径定理的推论.
(2)设⊙O的半径为r,在Rt△OPD中,利用勾股定理构建方程即可解决问题.
【详解】(1)过P点作AB的垂线交圆与C、D两点, CD就是所求的弦,如图.
依据:平分弦(非直径)的直径垂直于弦;
(2)如图,连接OD,
∵OA⊥CD于点P,AB是⊙O的直径,
∴∠OPD=90°,PD=CD,
∵CD=8,
∴PD=4.
设⊙O的半径为r,则OD=r,OP=OA﹣AP=r﹣2,
在Rt△ODP中,∠OPD=90°,
∴OD2=OP2+PD2,
即r2=(r﹣2)2+42,
解得r=5,
即⊙O的半径为5.
【点睛】本题主要考查了垂径定理,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
24.OE=OF,证明见解析.
【详解】试题分析:
过O作OM⊥AB于M,
∴AM=BM
∵AE=BF
∴EM="FM"
即OM垂直平分EF
∴OE=OF
考点:本题考查的是垂径定理,垂直平分线的性质
点评:解答本题的关键是熟练掌握垂直平分线的性质:垂直平分线上的点到线段两端的距离相等.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
