5.10圆锥的侧面积同步练习(含解析)
文档属性
| 名称 | 5.10圆锥的侧面积同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 922.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 15:44:09 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.10圆锥的侧面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.150° C.180° D.240°
2.如图是将一个圆锥的侧面展开得到的扇形纸片,已知该扇形的半径是,弧长是,则这个圆锥的高是( )
A. B. C. D.
3.若圆锥经过轴的剖面是正三角形,则它的侧面积与底面积之比为( )
A. B. C. D.
4.如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )
A. B. C. D.
5.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为 ( )
A.2 cm B.3 cm C.4 cm D.6 cm
6.已知一圆锥侧面展开图如图所示,则该圆锥的底面半径为( )
A. B.1 C.π D.2
7.已知圆锥的底面半径为,母线长为,那么圆锥侧面展开图所成扇形的圆心角为( )
A. B. C. D.
8.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( )
A.3 B.4 C. D.2
10.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
A.R=2r; B.; C.R=3r; D.R=4r.
11.如图,一个圆锥的底面半径为4,母线长为6 ,则这个圆锥的侧面积是( )
A.24 B. C.12 D.
12.一张半径为6cm的扇形纸片卷成一个圆锥的侧面,要求圆锥底面圆的半径为4cm,那么这张扇形纸片的圆心角度数是( )
A.150° B.240° C.200° D.180°
二、填空题
13.圆锥的底面半径为4,母线长为5.则这个圆锥的侧面积为 .
14.一个圆锥的主视图是边长为4cm的正三角形,则这个圆锥的侧面积等于 cm2.
15.如图,在扇形中,圆心角为,点与点的距离为.若扇形恰好是一个圆锥的侧面展开图,则该圆锥的底面圆半径为 .
16.在RtABC中,∠C=90°,AC=12,BC=5,将ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是
17.如图是一个几何体的三视图,其中主视图与左视图都是边长为4的等边三角形,则这个几何体的侧面展开图的面积为 .
三、解答题
18.已知在中,,,,将绕边所在的直线旋转一周得到一个圆锥,求该圆锥的全面积.
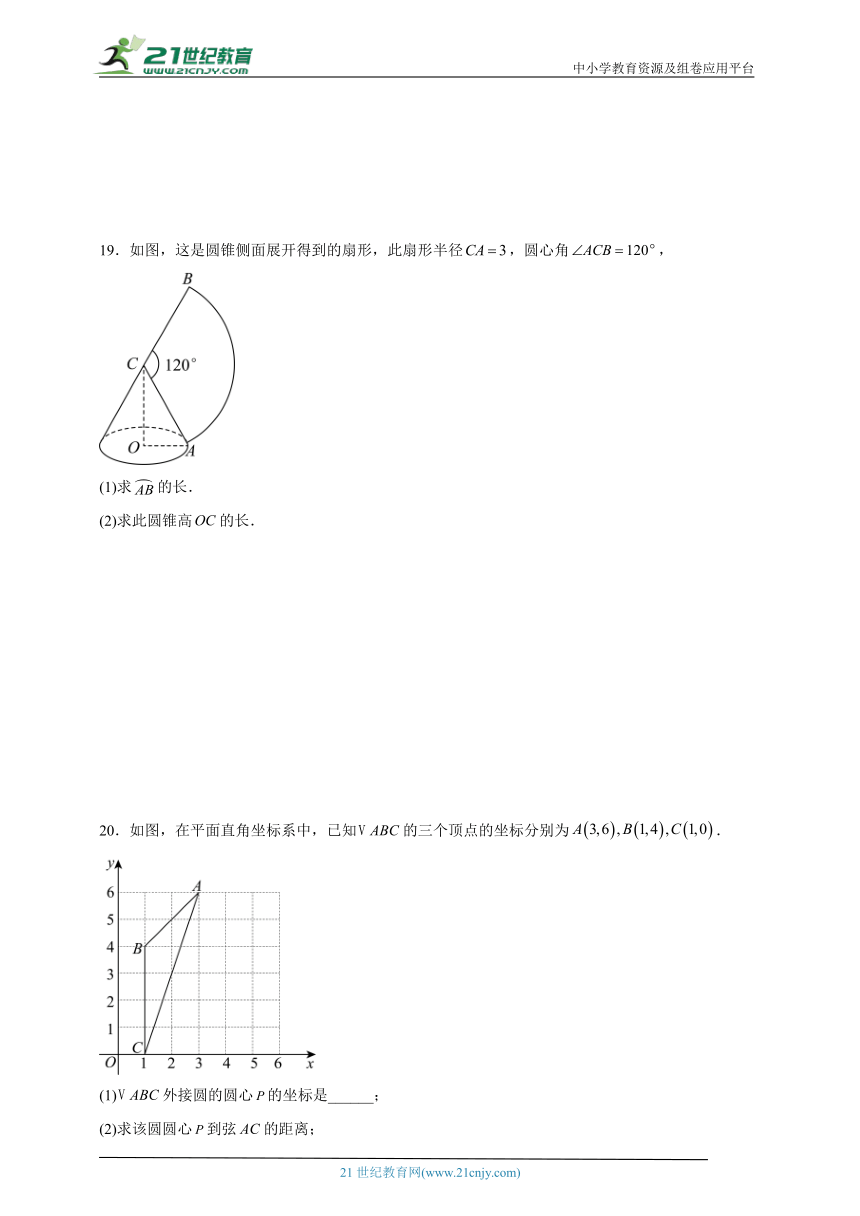
19.如图,这是圆锥侧面展开得到的扇形,此扇形半径,圆心角,
(1)求的长.
(2)求此圆锥高的长.
20.如图,在平面直角坐标系中,已知的三个顶点的坐标分别为.
(1)外接圆的圆心的坐标是______;
(2)求该圆圆心到弦的距离;
(3)以所在直线为旋转轴,将旋转一周,求所得几何体的表面积.
21.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.
22.如图,在扇形中,C是上一点,延长到D,且.
(1)求的度数;
(2)扇形是某圆锥的侧面展开图,若,求该圆锥的底面半径.
23.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
24.某外语学校要在圣诞节举行汇报演出,需要准备一些圣诞帽,为了培养学生的动手能力,学校决定自己制作这些圣诞帽.如果圣诞帽(圆锥形状)的规格是母线长为42厘米,底面直径为16厘米.
(1)求圣诞帽的侧面展开图(扇形)的圆心角的度数(精确到1度).
(2)已知A种规格的纸片能做3个圣诞帽,B种规格的纸片能做4个圣诞帽,汇报演出需要26个圣诞帽,写出A种规格的纸片 (张)与B种规格的纸片 (张)之间的函数关系式及的最大值与最小值;若自己制作时,A,B两种规格的纸片各买多少张时,才不会浪费纸张?
《5.10圆锥的侧面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C A B B D A B D
题号 11 12
答案 B B
1.C
【分析】根据圆锥的侧面积是底面积的2倍可得到圆锥底面半径和母线长的关系,利用圆锥侧面展开图的弧长=底面周长即可得到该圆锥的侧面展开图扇形的圆心角度数.
【详解】解:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=π,侧面面积=lR=πrR,
∵侧面积是底面积的2倍,
∴2π=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选:C.
【点睛】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长,以及利用扇形面积公式求出是解题的关键.
2.A
【分析】设圆锥的底面圆的半径为,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到,解方程得到,然后利用勾股定理计算圆锥的高.
【详解】解:设圆锥的底面圆的半径为,
根据题意得,
解得,
即圆锥的底面圆的半径为,
所以这个圆锥的高为.
故选:A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式.
3.C
【分析】本题考查圆锥的侧面积,设圆锥母线为t,底面半径为r,根据等边三角形的性质可得,再分别表示出圆锥的侧面积与底面积,即可求得结果.
【详解】设圆锥母线为t,底面半径为r,由题意得.
∴
∴
故选:C.
4.A
【分析】根据等腰三角形的性质得到的长,再利用弧长公式计算出弧的长,设圆锥的底面圆半径为,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长可得到.
【详解】过作于,
,
,
,
弧的长,
设圆锥的底面圆的半径为,则,解得.
故选A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
5.B
【详解】由题意知:底面周长=6πcm,
∴底面半径=6π÷2π=3cm.
故答案为B
6.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据这个扇形的弧长等于圆锥底面的周长列方程即可.
【详解】解:依题意,
解得:
故选:B.
7.D
【分析】设所给圆锥侧面展开图的圆心角是,根据圆锥底面圆周长=展开图扇形的弧长,构建方程求解即可.
【详解】解:设侧面展开图的圆心角是,
根据题意,得:,
解得:,
∴圆锥侧面展开图的圆心角是.
故选:D.
【点睛】本题考查圆锥的计算,解题的关键是理解圆锥底面圆周长=展开图扇形的弧长.
8.A
【分析】由底面圆的半径=5米,根据勾股定理求出母线长,利用圆锥的侧面面积公式,以及利用矩形的面积公式求得圆柱的侧面面积,最后求和.
【详解】解:∵底面半径=5米,圆锥高为2米,圆柱高为3米,
∴圆锥的母线长=米,
∴圆锥的侧面积=,
圆柱的侧面积=底面圆周长×圆柱高,
即,
故需要的毛毡:米,
故选:A.
【点睛】此题主要考查勾股定理,圆周长公式,圆锥侧面积,圆柱侧面积等,分别得出圆锥与圆柱侧面积是解题关键.
9.B
【分析】易得弧BC的长,然后求得弧BC所对的圆心角的度数,从而得到直角三角形,利用勾股定理求得CD的长即可.
【详解】解:如图:
∵,
∴设弧所对的圆心角的度数为n,
∴,
解得,
∴,
∴.
故选:B.
【点睛】求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.解题的关键是理解并掌握圆锥的弧长等于底面周长.
10.D
【详解】解:扇形的弧长是:,
圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:
∴即:R=4r,
r与R之间的关系是R=4r.
故选D.
11.B
【分析】根据圆锥的底面半径求得圆锥的底面周长,利用圆锥的底面周长等于侧面展开扇形的弧长求得圆锥的侧面积即可.本题考查了圆锥的计算,解题的关键是正确的利用圆锥的侧面展开扇形和圆锥的关系.
【详解】解:圆锥的底面半径长是4,
其底面周长为,
圆锥的底面周长等于侧面展开扇形的弧长,
圆锥的侧面积为:,
故选:B.
12.B
【分析】直接利用圆锥的底面圆的周长等于扇形弧长进而得出答案.
【详解】设这张扇形纸片的圆心角度数是n,
根据题意可得:=2×4π,
解得:n=240,
故选B.
【点睛】此题主要考查了圆锥的有关计算,掌握圆锥的底面圆的周长等于扇形弧长是解题关键.
13.
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【详解】解:该圆锥的侧面积.
故答案为:.
【点睛】本题考查了圆锥侧面积的计算.掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,是解题的关键.
14.
【分析】根据题意得圆锥的母线长为4cm,底面圆的半径为2cm,由弧长公式求出圆心角,根据扇形的面积公式求解即可.
【详解】解:根据题意得圆锥的母线长为4cm,底面圆的半径为2cm,
∴圆锥展开图的弧长为
解得
∴圆锥的展开图是半径为4cm的半圆
∴圆锥的侧面积为(cm2)
故答案为:.
【点睛】本题考查了弧长公式,扇形的面积,等边三角形的性质,主视图等知识.解题的关键在于明确圆锥展开图的半径与圆心角.
15.
【分析】连接,过O作于M,先求出扇形的半径,然后利用弧长=圆锥的底面周长这一等量关系可求解.
【详解】解:连接,过O作于M,
∵扇形中,圆心角为,
∴,
∵,
∴,,
∴,
∵
∴.
故答案为:.
【点睛】本题运用了弧长公式,垂径定理,等腰三角形的性质,解直角三角形,正确作出辅助线是解题的关键.
16.65π.
【详解】解:由勾股定理得AB=13,
由旋转知圆锥的底面半径为5,其侧面积为π=65π.
考点:圆锥的侧面积.
17.8π
【详解】解:由三视图可知这个几何体是一个圆锥,且底面圆的直径为4,母线长为4,
则底面周长为4π,
所以
所以扇形的圆心角的度数为180°,
则侧面展开图的面积为.
故答案为:8π
18.
【分析】本题考查圆锥表面积计算,先利用勾股定理求得,进而根据公式,熟练掌握勾股定理是解题的关键.
【详解】根据题意,得,
所以将绕边所在的直线旋转一周得到的圆锥的母线长为10,底面圆的半径为8,
所以该圆锥的侧面积为,底面圆的面积为,
所以该圆锥的全面积为.
19.(1)
(2)
【分析】(1)根据弧长公式进行求解即可;
(2)先求出底面半径,再用勾股定理求出圆锥的高即可.
【详解】(1)解:的长.
(2)设的长为r,则,解得.
在中,,
由勾股定理得.
20.(1)
(2)
(3)
【分析】(1)分别作的垂直平分线,即可解答;
(2)用中点公式求得的中点,再利用勾股定理即可解答;
(3)旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,据此求出表面积即可.
【详解】(1)解:如图,外接圆的圆心的坐标是,
故答案为:;
(2)解:根据中点公式,可得的中点,
(3)解:旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,
则他们的母线长为,,
所得表面积为.
【点睛】本题考查了外接圆、两点之间的距离公式、圆锥表面积公式,勾股定理,正确得到旋转后的图形是解题的关键.
21.4cm
【分析】设圆柱的母线长为l,根据圆柱的底面半径和轴截面面积,构造关于l的方程,解得答案.
【详解】:设圆柱的母线长为l,
∵圆柱的底面半径为3cm,轴截面面积为24cm2,
∴2×3×l=24,
解得:l=4cm,
即圆柱的母线长为4cm.
【点睛】本题考查的知识点是旋转体,其中正确理解圆柱轴截面的形状是解答的关键.
22.(1)150°
(2)5
【分析】对于(1),作一个圆周角,再求出这个角,然后根据圆周角定理求出答案即可;
对于(2),先根据弧长公式求出弧长,再根据圆锥的底面周长等于扇形的弧长列出等式,求出半径即可.
【详解】(1)根据题意作图如下:
作出所对的圆周角,
∵,,
∴,
∴;
(2)设该圆锥的底面半径为r,
根据题意得,
解得,
∴该圆锥的底面半径为5.
【点睛】本题主要考查了圆周角定理,弧长公式等,掌握扇形弧长与对应的圆锥的底面周长之间的关系是解题的关键.
23.(1)平方米;(2)米;
【分析】(1)先根据圆周角定理可得弦BC为直径,即可得到AB=AC,根据特殊角的锐角三角函数值可求得AB的长,最后根据扇形的面积公式即可求得结果;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,根据弧长公式及圆的周长公式即可求得结果.
【详解】(1)∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=
∴S阴影=S⊙O-S扇形ABC=()2-;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,由题意得
2r=,解得r=
答:(1)被剪掉的阴影部分的面积为;(2)该圆锥的底面圆半径是.
【点睛】圆周角定理,特殊角的锐角三角函数值,扇形的面积公式,弧长公式,计算能力是初中数学学习中一个极为重要的能力,是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.
24.(1) .(2) A,B两种规格的纸片各买6张、2张或2张、5张时,才不会浪费纸张.
【分析】(1)利用圆锥的弧长=圆锥的底面周长可得圆心角的度数;
(2)利用26个圣诞帽的个数列出相应的等量关系,可得y与x之间的函数关系式,然后取得整数解的最大值与最小值即可.
【详解】(1)∵底面直径为16厘米,
∴圆锥的底面周长为厘米.
∵圣诞帽的侧面展开图是一个扇形,
∴扇形的弧长是,
设扇形的圆心角为,则,
解得,则扇形的圆心角约是.
(2),由,得的最大值是,最小值是0.
显然,必须取整数,才不会浪费纸张.
由时,;时,时,;时,;时,时,,得A,B两种规格的纸片各买6张、2张或2张、5张时,才不会浪费纸张.
【点睛】用到的知识点为:圆锥的底面周长等于圆锥的侧面展开图的弧长;在较大的纸张上裁剪较小的图形,应从实际出发思考.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
5.10圆锥的侧面积
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一个圆锥的侧面积是底面积的2倍,则圆锥侧面展开图的扇形的圆心角是( )
A.120° B.150° C.180° D.240°
2.如图是将一个圆锥的侧面展开得到的扇形纸片,已知该扇形的半径是,弧长是,则这个圆锥的高是( )
A. B. C. D.
3.若圆锥经过轴的剖面是正三角形,则它的侧面积与底面积之比为( )
A. B. C. D.
4.如图,从一张腰长为,顶角为的等腰三角形铁皮中剪出一个最大的扇形,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为( )
A. B. C. D.
5.用一个半径长为6cm的半圆围成一个圆锥的侧面,则此圆锥的底面半径为 ( )
A.2 cm B.3 cm C.4 cm D.6 cm
6.已知一圆锥侧面展开图如图所示,则该圆锥的底面半径为( )
A. B.1 C.π D.2
7.已知圆锥的底面半径为,母线长为,那么圆锥侧面展开图所成扇形的圆心角为( )
A. B. C. D.
8.如图,蒙古包可以近似地看作是由圆锥和圆柱组成,若用毛毡搭建一个底面半径为5米,圆柱高3米,圆锥高2米的蒙古包,则需要毛毡的面积为( )
A.米2 B.米2
C.米2 D.米2
9.如图,圆锥的底面半径R=3,母线l=5dm,AB为底面直径,C为底面圆周上一点,∠COB=150°,D为VB上一点,VD=.现有一只蚂蚁,沿圆锥表面从点C爬到D.则蚂蚁爬行的最短路程是( )
A.3 B.4 C. D.2
10.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为r,扇形的半径为R,扇形的圆心角等于90°,则r与R之间的关系是( )
A.R=2r; B.; C.R=3r; D.R=4r.
11.如图,一个圆锥的底面半径为4,母线长为6 ,则这个圆锥的侧面积是( )
A.24 B. C.12 D.
12.一张半径为6cm的扇形纸片卷成一个圆锥的侧面,要求圆锥底面圆的半径为4cm,那么这张扇形纸片的圆心角度数是( )
A.150° B.240° C.200° D.180°
二、填空题
13.圆锥的底面半径为4,母线长为5.则这个圆锥的侧面积为 .
14.一个圆锥的主视图是边长为4cm的正三角形,则这个圆锥的侧面积等于 cm2.
15.如图,在扇形中,圆心角为,点与点的距离为.若扇形恰好是一个圆锥的侧面展开图,则该圆锥的底面圆半径为 .
16.在RtABC中,∠C=90°,AC=12,BC=5,将ABC绕边AC所在直线旋转一周得到圆锥,则该圆锥的侧面积是
17.如图是一个几何体的三视图,其中主视图与左视图都是边长为4的等边三角形,则这个几何体的侧面展开图的面积为 .
三、解答题
18.已知在中,,,,将绕边所在的直线旋转一周得到一个圆锥,求该圆锥的全面积.
19.如图,这是圆锥侧面展开得到的扇形,此扇形半径,圆心角,
(1)求的长.
(2)求此圆锥高的长.
20.如图,在平面直角坐标系中,已知的三个顶点的坐标分别为.
(1)外接圆的圆心的坐标是______;
(2)求该圆圆心到弦的距离;
(3)以所在直线为旋转轴,将旋转一周,求所得几何体的表面积.
21.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.
22.如图,在扇形中,C是上一点,延长到D,且.
(1)求的度数;
(2)扇形是某圆锥的侧面展开图,若,求该圆锥的底面半径.
23.有一个直径为1m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC,如图所示.
(1)求被剪掉阴影部分的面积:
(2)用所留的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径是多少?
24.某外语学校要在圣诞节举行汇报演出,需要准备一些圣诞帽,为了培养学生的动手能力,学校决定自己制作这些圣诞帽.如果圣诞帽(圆锥形状)的规格是母线长为42厘米,底面直径为16厘米.
(1)求圣诞帽的侧面展开图(扇形)的圆心角的度数(精确到1度).
(2)已知A种规格的纸片能做3个圣诞帽,B种规格的纸片能做4个圣诞帽,汇报演出需要26个圣诞帽,写出A种规格的纸片 (张)与B种规格的纸片 (张)之间的函数关系式及的最大值与最小值;若自己制作时,A,B两种规格的纸片各买多少张时,才不会浪费纸张?
《5.10圆锥的侧面积》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A C A B B D A B D
题号 11 12
答案 B B
1.C
【分析】根据圆锥的侧面积是底面积的2倍可得到圆锥底面半径和母线长的关系,利用圆锥侧面展开图的弧长=底面周长即可得到该圆锥的侧面展开图扇形的圆心角度数.
【详解】解:设母线长为R,底面半径为r,
∴底面周长=2πr,底面面积=π,侧面面积=lR=πrR,
∵侧面积是底面积的2倍,
∴2π=πrR,
∴R=2r,
设圆心角为n,有=2πr=πR,
∴n=180°.
故选:C.
【点睛】本题综合考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长,以及利用扇形面积公式求出是解题的关键.
2.A
【分析】设圆锥的底面圆的半径为,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长得到,解方程得到,然后利用勾股定理计算圆锥的高.
【详解】解:设圆锥的底面圆的半径为,
根据题意得,
解得,
即圆锥的底面圆的半径为,
所以这个圆锥的高为.
故选:A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.也考查了弧长公式.
3.C
【分析】本题考查圆锥的侧面积,设圆锥母线为t,底面半径为r,根据等边三角形的性质可得,再分别表示出圆锥的侧面积与底面积,即可求得结果.
【详解】设圆锥母线为t,底面半径为r,由题意得.
∴
∴
故选:C.
4.A
【分析】根据等腰三角形的性质得到的长,再利用弧长公式计算出弧的长,设圆锥的底面圆半径为,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长可得到.
【详解】过作于,
,
,
,
弧的长,
设圆锥的底面圆的半径为,则,解得.
故选A.
【点睛】本题考查了圆锥的计算:圆锥的侧面展开图为扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.
5.B
【详解】由题意知:底面周长=6πcm,
∴底面半径=6π÷2π=3cm.
故答案为B
6.B
【分析】本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.根据这个扇形的弧长等于圆锥底面的周长列方程即可.
【详解】解:依题意,
解得:
故选:B.
7.D
【分析】设所给圆锥侧面展开图的圆心角是,根据圆锥底面圆周长=展开图扇形的弧长,构建方程求解即可.
【详解】解:设侧面展开图的圆心角是,
根据题意,得:,
解得:,
∴圆锥侧面展开图的圆心角是.
故选:D.
【点睛】本题考查圆锥的计算,解题的关键是理解圆锥底面圆周长=展开图扇形的弧长.
8.A
【分析】由底面圆的半径=5米,根据勾股定理求出母线长,利用圆锥的侧面面积公式,以及利用矩形的面积公式求得圆柱的侧面面积,最后求和.
【详解】解:∵底面半径=5米,圆锥高为2米,圆柱高为3米,
∴圆锥的母线长=米,
∴圆锥的侧面积=,
圆柱的侧面积=底面圆周长×圆柱高,
即,
故需要的毛毡:米,
故选:A.
【点睛】此题主要考查勾股定理,圆周长公式,圆锥侧面积,圆柱侧面积等,分别得出圆锥与圆柱侧面积是解题关键.
9.B
【分析】易得弧BC的长,然后求得弧BC所对的圆心角的度数,从而得到直角三角形,利用勾股定理求得CD的长即可.
【详解】解:如图:
∵,
∴设弧所对的圆心角的度数为n,
∴,
解得,
∴,
∴.
故选:B.
【点睛】求立体图形中两点之间的最短路线长,一般应放在平面内,构造直角三角形,求两点之间的线段的长度.解题的关键是理解并掌握圆锥的弧长等于底面周长.
10.D
【详解】解:扇形的弧长是:,
圆的半径为r,则底面圆的周长是2πr,
圆锥的底面周长等于侧面展开图的扇形弧长则得到:
∴即:R=4r,
r与R之间的关系是R=4r.
故选D.
11.B
【分析】根据圆锥的底面半径求得圆锥的底面周长,利用圆锥的底面周长等于侧面展开扇形的弧长求得圆锥的侧面积即可.本题考查了圆锥的计算,解题的关键是正确的利用圆锥的侧面展开扇形和圆锥的关系.
【详解】解:圆锥的底面半径长是4,
其底面周长为,
圆锥的底面周长等于侧面展开扇形的弧长,
圆锥的侧面积为:,
故选:B.
12.B
【分析】直接利用圆锥的底面圆的周长等于扇形弧长进而得出答案.
【详解】设这张扇形纸片的圆心角度数是n,
根据题意可得:=2×4π,
解得:n=240,
故选B.
【点睛】此题主要考查了圆锥的有关计算,掌握圆锥的底面圆的周长等于扇形弧长是解题关键.
13.
【分析】根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式求解.
【详解】解:该圆锥的侧面积.
故答案为:.
【点睛】本题考查了圆锥侧面积的计算.掌握圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长,是解题的关键.
14.
【分析】根据题意得圆锥的母线长为4cm,底面圆的半径为2cm,由弧长公式求出圆心角,根据扇形的面积公式求解即可.
【详解】解:根据题意得圆锥的母线长为4cm,底面圆的半径为2cm,
∴圆锥展开图的弧长为
解得
∴圆锥的展开图是半径为4cm的半圆
∴圆锥的侧面积为(cm2)
故答案为:.
【点睛】本题考查了弧长公式,扇形的面积,等边三角形的性质,主视图等知识.解题的关键在于明确圆锥展开图的半径与圆心角.
15.
【分析】连接,过O作于M,先求出扇形的半径,然后利用弧长=圆锥的底面周长这一等量关系可求解.
【详解】解:连接,过O作于M,
∵扇形中,圆心角为,
∴,
∵,
∴,,
∴,
∵
∴.
故答案为:.
【点睛】本题运用了弧长公式,垂径定理,等腰三角形的性质,解直角三角形,正确作出辅助线是解题的关键.
16.65π.
【详解】解:由勾股定理得AB=13,
由旋转知圆锥的底面半径为5,其侧面积为π=65π.
考点:圆锥的侧面积.
17.8π
【详解】解:由三视图可知这个几何体是一个圆锥,且底面圆的直径为4,母线长为4,
则底面周长为4π,
所以
所以扇形的圆心角的度数为180°,
则侧面展开图的面积为.
故答案为:8π
18.
【分析】本题考查圆锥表面积计算,先利用勾股定理求得,进而根据公式,熟练掌握勾股定理是解题的关键.
【详解】根据题意,得,
所以将绕边所在的直线旋转一周得到的圆锥的母线长为10,底面圆的半径为8,
所以该圆锥的侧面积为,底面圆的面积为,
所以该圆锥的全面积为.
19.(1)
(2)
【分析】(1)根据弧长公式进行求解即可;
(2)先求出底面半径,再用勾股定理求出圆锥的高即可.
【详解】(1)解:的长.
(2)设的长为r,则,解得.
在中,,
由勾股定理得.
20.(1)
(2)
(3)
【分析】(1)分别作的垂直平分线,即可解答;
(2)用中点公式求得的中点,再利用勾股定理即可解答;
(3)旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,据此求出表面积即可.
【详解】(1)解:如图,外接圆的圆心的坐标是,
故答案为:;
(2)解:根据中点公式,可得的中点,
(3)解:旋转后的几何体为半径为2,高为6的圆锥,减去半径为2,高为2的圆锥,
则他们的母线长为,,
所得表面积为.
【点睛】本题考查了外接圆、两点之间的距离公式、圆锥表面积公式,勾股定理,正确得到旋转后的图形是解题的关键.
21.4cm
【分析】设圆柱的母线长为l,根据圆柱的底面半径和轴截面面积,构造关于l的方程,解得答案.
【详解】:设圆柱的母线长为l,
∵圆柱的底面半径为3cm,轴截面面积为24cm2,
∴2×3×l=24,
解得:l=4cm,
即圆柱的母线长为4cm.
【点睛】本题考查的知识点是旋转体,其中正确理解圆柱轴截面的形状是解答的关键.
22.(1)150°
(2)5
【分析】对于(1),作一个圆周角,再求出这个角,然后根据圆周角定理求出答案即可;
对于(2),先根据弧长公式求出弧长,再根据圆锥的底面周长等于扇形的弧长列出等式,求出半径即可.
【详解】(1)根据题意作图如下:
作出所对的圆周角,
∵,,
∴,
∴;
(2)设该圆锥的底面半径为r,
根据题意得,
解得,
∴该圆锥的底面半径为5.
【点睛】本题主要考查了圆周角定理,弧长公式等,掌握扇形弧长与对应的圆锥的底面周长之间的关系是解题的关键.
23.(1)平方米;(2)米;
【分析】(1)先根据圆周角定理可得弦BC为直径,即可得到AB=AC,根据特殊角的锐角三角函数值可求得AB的长,最后根据扇形的面积公式即可求得结果;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,根据弧长公式及圆的周长公式即可求得结果.
【详解】(1)∵∠BAC=90°
∴弦BC为直径
∴AB=AC
∴AB=AC=BC·sin45°=
∴S阴影=S⊙O-S扇形ABC=()2-;
(2)设圆锥底面圆的半径为r,而弧BC的长即为圆锥底面的周长,由题意得
2r=,解得r=
答:(1)被剪掉的阴影部分的面积为;(2)该圆锥的底面圆半径是.
【点睛】圆周角定理,特殊角的锐角三角函数值,扇形的面积公式,弧长公式,计算能力是初中数学学习中一个极为重要的能力,是中考的热点,在各种题型中均有出现,一般难度不大,需特别注意.
24.(1) .(2) A,B两种规格的纸片各买6张、2张或2张、5张时,才不会浪费纸张.
【分析】(1)利用圆锥的弧长=圆锥的底面周长可得圆心角的度数;
(2)利用26个圣诞帽的个数列出相应的等量关系,可得y与x之间的函数关系式,然后取得整数解的最大值与最小值即可.
【详解】(1)∵底面直径为16厘米,
∴圆锥的底面周长为厘米.
∵圣诞帽的侧面展开图是一个扇形,
∴扇形的弧长是,
设扇形的圆心角为,则,
解得,则扇形的圆心角约是.
(2),由,得的最大值是,最小值是0.
显然,必须取整数,才不会浪费纸张.
由时,;时,时,;时,;时,时,,得A,B两种规格的纸片各买6张、2张或2张、5张时,才不会浪费纸张.
【点睛】用到的知识点为:圆锥的底面周长等于圆锥的侧面展开图的弧长;在较大的纸张上裁剪较小的图形,应从实际出发思考.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
