2025年中考数学二轮复习 专题9 三角形、四边形的相关计算 课件 (共53张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习 专题9 三角形、四边形的相关计算 课件 (共53张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览








文档简介
(共53张PPT)
专题九 三角形、四边形的相关计算
类型一 利用勾股定理求线段长
在图形中遇到求线段的长时,有时可以利用图形中的直角三角形
(或通过作垂线将待求线段放入某个直角三角形中),通过勾股定理
来解决问题.
1. 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为BC边上
一点,连接AP,若AP= ,则PC的长为 或 .
或
2. [2024·达州]如图,在Rt△ABC中,∠C=90°,点D在线段BC上,
且∠BAD=45°,若AC=4,CD=1,则△ABC的面积是 .
3. 如图,在边长为1的正方形ABCD中,E为AD的中点,连接BE,将
△ABE沿BE折叠得到△FBE,EG∥DC,交BF于点G,则EG的长
为 .
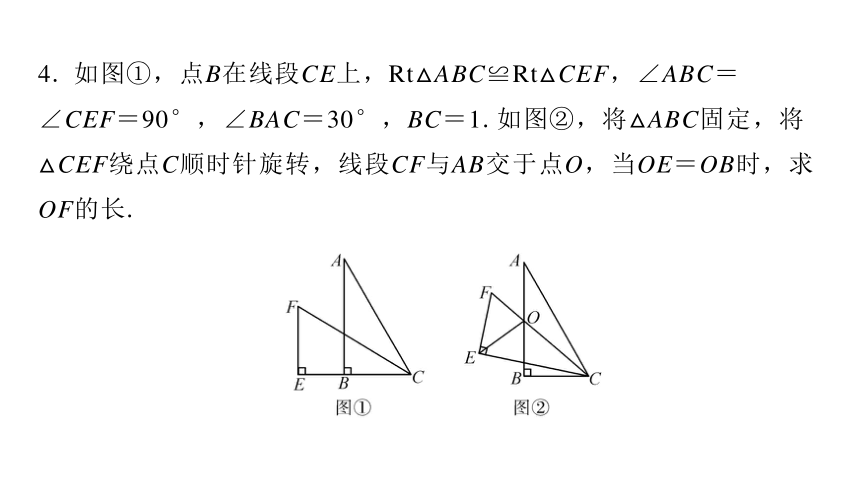
4. 如图①,点B在线段CE上,Rt△ABC≌Rt△CEF,∠ABC=
∠CEF=90°,∠BAC=30°,BC=1.如图②,将△ABC固定,将
△CEF绕点C顺时针旋转,线段CF与AB交于点O,当OE=OB时,求
OF的长.
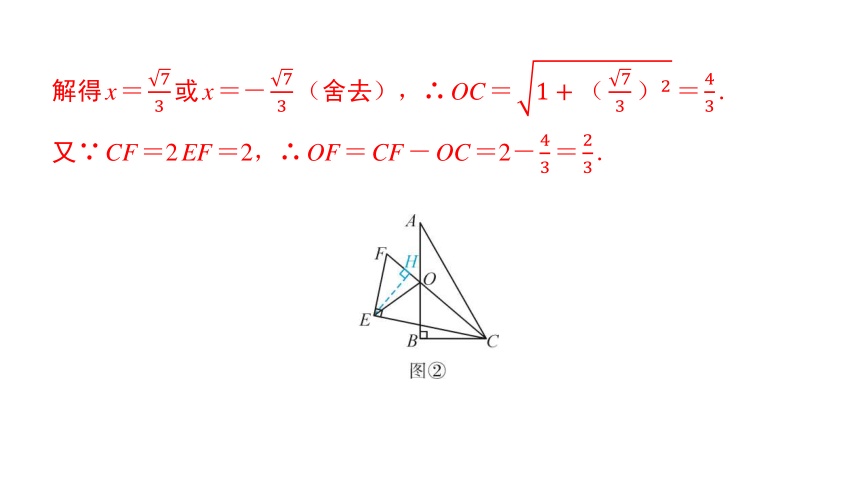
解:如图②,过点E作EH⊥CF于点H. 设OB=OE=x(x>0).
∵EF=1,∠ECF=30°,EH⊥CF,
∴EC= EF= ,∴EH= ,CH= EH= ,
∴OC= = ,∴OH=CH-OC= - .
∵OE2=EH2+OH2,∴x2= + ,
解得x= 或x=- (舍去),∴OC= = .
又∵CF=2EF=2,∴OF=CF-OC=2- = .
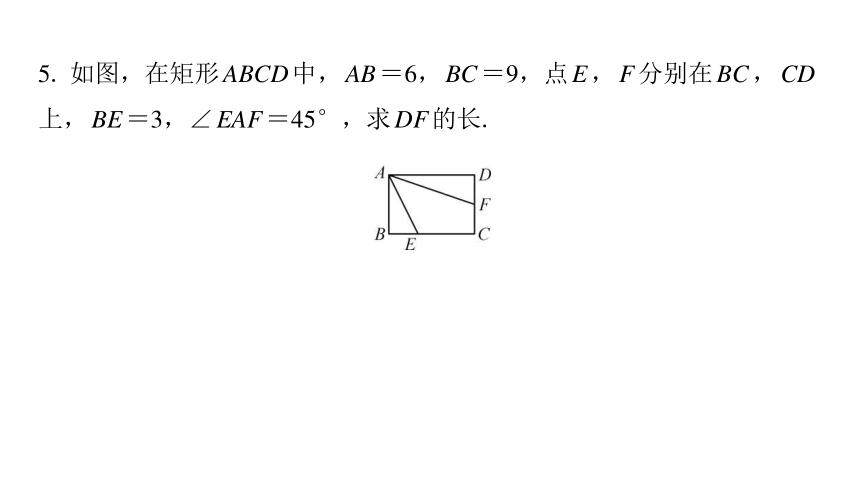
5. 如图,在矩形ABCD中,AB=6,BC=9,点E,F分别在BC,CD
上,BE=3,∠EAF=45°,求DF的长.
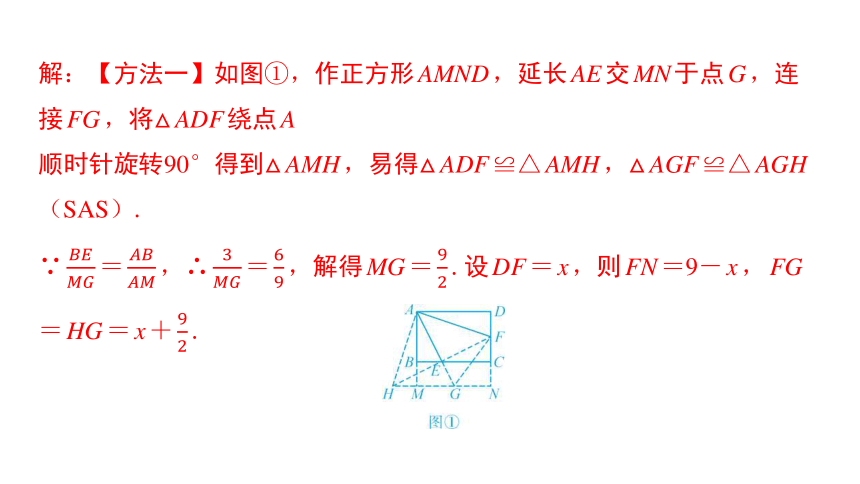
解:【方法一】如图①,作正方形AMND,延长AE交MN于点G,连
接FG,将△ADF绕点A
顺时针旋转90°得到△AMH,易得△ADF≌△AMH,△AGF≌△AGH
(SAS).
∵ = ,∴ = ,解得MG= .设DF=x,则FN=9-x,FG
=HG=x+ .
∵FG2=FN2+NG2,∴ =(9-x)2+ ,解得x=3,
即DF=3.
【方法二】如图①,连接HF. 易得AG垂直平分HF,
△AMG∽△HNF,
∴ = ,∴ = ,解得x=3,即DF=3.
【方法三】如图②,过点F作FG⊥AF,交AE的延长线于点G,过点G作BC的平行线,
分别交AB,DC的延长线于点M,N. 易得△AFG为等腰直角三角形,△ADF≌△FNG(AAS).
设DF=x,则NG=DF=x,MG=9-x.
∵ = ,∴ = ,解得x=3,即DF=3.
类型二 利用相似求线段长或线段比
在图形中遇到求线段长或线段比时,有时可以利用图形中的相似
三角形,通过相似三角形的性质得到线段比或建立待求线段的相似比
方程来解决问题.若图形中没有相似三角形,有时还需要通过作平行线
或垂线构造与待求线段相关的相似三角形.
1. 如图,在△ABC中,∠B=45°,AB=6,BC=4 ,D为BC上一
点,且∠DAC=45°,则BD的长为 .
2. 如图,在△ABC中,点O在边BC上,∠BAO=30°,∠OAC=
75°,AO=3 ,BO∶CO=1∶3,则AB的长为 4 .
4
3. [2024·宜宾]如图,正五边形ABCDE的边长为4,则这个正五边形的对
角线AC的长是 .
2 +2
4. 如图,在正六边形ABCDEF中,M为CD的中点,点N在边BC上,
且CN=2BN,AM与FN相交于点P, 的值为 .
5. 如图,在△ABC中,AB=3,AC=2,P为AB边上一点,M为CP
的中点,若∠PBM=∠ACP,求BP的长.
解:如图,过点M作MN∥AC,交AB于点N,则MN为△APC的中位线,
∴MN= AC=1,∠NMP=∠ACP=∠PBM.
又∵∠PNM=∠MNB,∴△NPM∽△NMB,∴ = .
设AN=NP=x,则 = ,解得x1= (舍去),x2= ,
∴BP=AB-AP=3-2x=3-2× = .
6. 如图,在等边三角形ABC中,AB=3,D是CB延长线上一点,且
BD=1.点E在直线AC上,当∠BAD=∠CDE时,求AE的长.
解:分以下两种情况讨论.
如图①,点E在线段AC的延长线上时.
∵∠ABD=∠DCE=120°,∠BAD=∠CDE,∴△ABD∽△DCE,
∴ = ,即 = ,解得CE= ,∴AE=AC+CE=3+ = .
如图②,点E在线段AC上时,过点E作EF∥AB,交BC于点F,则
△EFC为等边三角形.
∵∠ABD=∠BFE=120°,∠BAD=∠CDE,∴△ABD∽△DFE,
∴ = ,即 = ,解得DF=3EF=3CF.
∵CD=DF+CF=4,∴3CF+CF=4,解得CF=1,∴CE=CF=
1,AE=AC-CE=2.
综上所述,当∠BAD=∠CDE时,AE的长为2或 .
7. 在△ABC中,∠ACB=90°,AC=BC,D为AB上一点.
(1)如图①,H为CD上一动点,过点H作EF⊥CD,交BC于点E,
交AC于点F,若 = ,求 的值;
解:(1)如图①,过点A作AM∥BC,交CD的延长线于
点M,
∴△ADM∽△BDC,∴ = = = ,
∴tan∠ACM= ,∴tan∠HCF=tan∠CEH= ,
∴ = , = ,∴ = .
(2)如图②,点H在CD上,且∠AHD=45°,CH=DH,求 的
值.
解:(2)如图②,过点D作DN⊥AC于点N. 设CH=
DH= DC=x.
∵∠AHD=∠CAD=45°,∠ADH=∠CDA,
∴△ADH∽△CDA,∴AD2=HD·CD=2x2,
∴AD= x,AN=DN= AD=x,∴CN= = = x,∴ = = = .
类型三 构造全等三角形求线段长
在图形中遇到求线段长时,有时通过作垂线或平行线的方法构造
全等三角形,利用全等三角形的性质达到与已知线段长的等量转换,
再结合勾股定理、相似三角形等相关知识求解.
1. 如图,在四边形ABCD中,对角线AC,BD相交于点E,且E为对角
线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,求
AC的长.
解:如图,过点D作DM∥BC,交AC于点M. 易得△DEM≌△BEC
(ASA或AAS),
∴DM=BC=2,ME=CE=1,∠DME=∠BCE=120°,∴∠AMD
=60°.
又∵∠DAE=30°,∴∠ADM=90°,∴AM=2DM=4,∴AC=
AM+MC=4+2=6.
2. 如图,在△ABC中,∠ACB=90°,AC=BC=4,P为△ABC内一
点,连接AP,BP,CP,其中CP的延长线交AB于点E,若∠CBP=
∠PCB=15°,求AP的长.
解:如图,过点A作AM⊥CE于点M,过点B作BN⊥CE,交CE的延长线于点N.
易得△ACM≌△CBN(AAS).设BN=CM=x.∵∠CBP=∠PCB=15°,∴∠BPN=30°,
∴CP=BP=2BN=2x,∴PM=CM=x,∴AM为CP的垂直平分线,∴AP=AC=4.
3. 如图,在△ABC中,∠A=∠ACB,AC=2,点P在边AB上,Q在
BC的延长线上,且PA=QC,连接PQ交AC于点D,PE⊥AC于点
E,求DE的长.
解:如图,过点P作PF∥BC,交AC于点F,
∴∠A=∠ACB=∠AFP,∴PA=PF. 又∵PE⊥AC,∴EF= AF.
∵∠PFD=∠QCD,∠PDF=∠QDC,PF=PA=QC,∴△PDF≌△QDC(AAS),
∴DF=DC,∴DE=EF+DF= AF+ FC= AC= ×2=1.
4. 如图,在△ABC中,∠ACB=90°,AC=BC=4,D为AC的中
点,CH⊥BD于点H,O为AB的中点,连接OH,求OH的长.
解:如图,连接CO,过点O作OE⊥OH,交BD于点E. 易得CO=BO,∠HOC=∠EOB.
∵∠ACO=∠OBC=45°,∠DCH=∠HBC,∴∠OCH=∠OBE,
∴△OCH≌△OBE(ASA),∴OH=OE,CH=BE.
∵CD=2,BC=4,
∴BD= =2 .∵ BD·CH= CD·BC,∴CH=BE= .
又∵BH= = ,∴HE=BH-BE= .
∵△OEH是等腰直角三角形,∴OH= HE=× = .
类型四 利用旋转变换求线段长
当遇到“从一点(O)呈放射状发射出三条线段(OA,OB,
OC),且其中有两条线段相等(OA=OB,OA与OB的夹角为α)”
的几何图形,求某线段长时,往往可以以点O为旋转中心,将以OA
(或OB)为边的一个三角形旋转α度,使其与OB(或OA)重合,构
造出“手拉手模型”,实现线段的等量转换,图形重构.
1. 如图,在△ABC中,∠ABC=45°,AB= ,BC=4,以AC为直
角边作等腰直角三角形ACD,连接BD,求BD的长.
解:如图,将△ABD绕点A顺时针旋转90°得到△AEC,连接BE.
易得△AEC≌△ABD,△ABE为等腰直角三角形,
∴BD=EC,EB= AB= × =3.
∵∠ABC=∠ABE=45°,∴∠EBC=90°,∴BD=EC= = =5.
2. 如图,E为菱形ABCD外一点,∠BEA=∠ABC=60°,AE=3,
BE=5,求DE的长.
解:如图,将△EAD绕点A顺时针旋转120°得到△FAB,连接EF,过点A作AM⊥EF于点M.
易得△FAB≌△EAD,AF=AE,BF=DE,∠EAF=∠BAD=120°,
∴∠AEF=(180°-120°)÷2=30°,∠BEF=∠AEF+∠BEA=90°.
∵AM= AE= ,EM= = ,
∴EF=2EM=3 ,∴DE=BF= =
=2 .
3. 如图,P是正方形ABCD内一点,且点P到点A,B,C的距离分别
为2 , ,4,求正方形ABCD的面积.
解:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于点H.
∵BP=BM= ,∠PBM=90°,∴PM= BM=2.∵PC=4,PA=MC=2 ,
∴PC2=CM2+PM2,∴∠PMC=90°.∵∠BPM=∠BMP=45°,
∴∠CMB=∠APB=135°,∴∠APB+∠BPM=180°,∴A,P,M三点共线.
∵BH⊥PM,∴PH=HM,∴BH=PH=HM=1,
∴AH=2 +1,
∴AB2=AH2+BH2=(2 +1)2+12=14+4 ,∴
正方形ABCD的面积为14+4 .
4. 如图,B,C为△ADE的边DE上两点,∠BAC=90°,AB=AC.
若∠DAE=135°,BD=2,CE=3,求AB的长.
解:如图,将△ABE绕点A逆时针旋转90°得到
△ACF,连接DF. 易得△ACF≌△ABE,
∴CF=BE,AF=AE,∠ACF=∠ABE. ∵∠BAC
=90°,AB=AC,
∴∠ACF=∠ABE=∠ACB=45°,∴∠DCF=
90°,即△DCF为直角三角形.
∵∠DAE=135°,∠FAE=90°,∴∠DAF=360°
-∠DAE-∠FAE=135°,
∴∠DAE=∠DAF. 又∵AF=AE,AD=AD,
∴△ADE≌△ADF(SAS),
∴DF=DE. 设BC=x,则CF=BE=x+3,DF=DE=x+5,
DC=x+2.
在Rt△FCD中,DF2=DC2+CF2,∴(x+5)2=(x+2)2+
(x+3)2,解得x=2 或x=-2 (舍去).
∴BC=2 ,∴AB= BC= .
5. 如图,在△ABC中,∠ABC=60°,AB=6,BC=10,以AC为边
向外作等边三角形ACD,连接BD,求BD的长.
解:如图,将△ABD绕点A顺时针旋转60°得到△AEC,连接BE.
易得△AEC≌△ABD,△ABE为等边三角形,∴BD=EC,
EB=AB=6,∠EBC=120°.
过点E作EF⊥CB,交CB的延长线于点F(如图),则∠BEF=
∠EBC-∠F=30°,
∴BF= EB=3,EF= =3 ,
∴BD=EC= = =14.
6. [2024·宜宾改编]如图,在△ABC中,AB=3 ,AC=2,以BC为
边作Rt△BCD,BC=BD,点D与点A在BC的两侧,求AD的最大值.
解:如图,将BA绕点B顺时针旋转90°至BE,连接AE,DE.
∵BE=BA,∠ABE=90°,∴AE= AB= ×3 =6.
∵∠DBC=∠EBA=90°,∴∠DBE=∠CBA. 又∵BD=BC,
BE=BA,
∴△DBE≌△CBA(SAS),∴DE=CA=2.
∵在△ADE中,由三角形三边关系可得AD<AE+DE,
∴当A,D,E三点共线时,AD有最大值,
∴AD的最大值为DE+AE=2+6=8.
谢谢观看
专题九 三角形、四边形的相关计算
类型一 利用勾股定理求线段长
在图形中遇到求线段的长时,有时可以利用图形中的直角三角形
(或通过作垂线将待求线段放入某个直角三角形中),通过勾股定理
来解决问题.
1. 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为BC边上
一点,连接AP,若AP= ,则PC的长为 或 .
或
2. [2024·达州]如图,在Rt△ABC中,∠C=90°,点D在线段BC上,
且∠BAD=45°,若AC=4,CD=1,则△ABC的面积是 .
3. 如图,在边长为1的正方形ABCD中,E为AD的中点,连接BE,将
△ABE沿BE折叠得到△FBE,EG∥DC,交BF于点G,则EG的长
为 .
4. 如图①,点B在线段CE上,Rt△ABC≌Rt△CEF,∠ABC=
∠CEF=90°,∠BAC=30°,BC=1.如图②,将△ABC固定,将
△CEF绕点C顺时针旋转,线段CF与AB交于点O,当OE=OB时,求
OF的长.
解:如图②,过点E作EH⊥CF于点H. 设OB=OE=x(x>0).
∵EF=1,∠ECF=30°,EH⊥CF,
∴EC= EF= ,∴EH= ,CH= EH= ,
∴OC= = ,∴OH=CH-OC= - .
∵OE2=EH2+OH2,∴x2= + ,
解得x= 或x=- (舍去),∴OC= = .
又∵CF=2EF=2,∴OF=CF-OC=2- = .
5. 如图,在矩形ABCD中,AB=6,BC=9,点E,F分别在BC,CD
上,BE=3,∠EAF=45°,求DF的长.
解:【方法一】如图①,作正方形AMND,延长AE交MN于点G,连
接FG,将△ADF绕点A
顺时针旋转90°得到△AMH,易得△ADF≌△AMH,△AGF≌△AGH
(SAS).
∵ = ,∴ = ,解得MG= .设DF=x,则FN=9-x,FG
=HG=x+ .
∵FG2=FN2+NG2,∴ =(9-x)2+ ,解得x=3,
即DF=3.
【方法二】如图①,连接HF. 易得AG垂直平分HF,
△AMG∽△HNF,
∴ = ,∴ = ,解得x=3,即DF=3.
【方法三】如图②,过点F作FG⊥AF,交AE的延长线于点G,过点G作BC的平行线,
分别交AB,DC的延长线于点M,N. 易得△AFG为等腰直角三角形,△ADF≌△FNG(AAS).
设DF=x,则NG=DF=x,MG=9-x.
∵ = ,∴ = ,解得x=3,即DF=3.
类型二 利用相似求线段长或线段比
在图形中遇到求线段长或线段比时,有时可以利用图形中的相似
三角形,通过相似三角形的性质得到线段比或建立待求线段的相似比
方程来解决问题.若图形中没有相似三角形,有时还需要通过作平行线
或垂线构造与待求线段相关的相似三角形.
1. 如图,在△ABC中,∠B=45°,AB=6,BC=4 ,D为BC上一
点,且∠DAC=45°,则BD的长为 .
2. 如图,在△ABC中,点O在边BC上,∠BAO=30°,∠OAC=
75°,AO=3 ,BO∶CO=1∶3,则AB的长为 4 .
4
3. [2024·宜宾]如图,正五边形ABCDE的边长为4,则这个正五边形的对
角线AC的长是 .
2 +2
4. 如图,在正六边形ABCDEF中,M为CD的中点,点N在边BC上,
且CN=2BN,AM与FN相交于点P, 的值为 .
5. 如图,在△ABC中,AB=3,AC=2,P为AB边上一点,M为CP
的中点,若∠PBM=∠ACP,求BP的长.
解:如图,过点M作MN∥AC,交AB于点N,则MN为△APC的中位线,
∴MN= AC=1,∠NMP=∠ACP=∠PBM.
又∵∠PNM=∠MNB,∴△NPM∽△NMB,∴ = .
设AN=NP=x,则 = ,解得x1= (舍去),x2= ,
∴BP=AB-AP=3-2x=3-2× = .
6. 如图,在等边三角形ABC中,AB=3,D是CB延长线上一点,且
BD=1.点E在直线AC上,当∠BAD=∠CDE时,求AE的长.
解:分以下两种情况讨论.
如图①,点E在线段AC的延长线上时.
∵∠ABD=∠DCE=120°,∠BAD=∠CDE,∴△ABD∽△DCE,
∴ = ,即 = ,解得CE= ,∴AE=AC+CE=3+ = .
如图②,点E在线段AC上时,过点E作EF∥AB,交BC于点F,则
△EFC为等边三角形.
∵∠ABD=∠BFE=120°,∠BAD=∠CDE,∴△ABD∽△DFE,
∴ = ,即 = ,解得DF=3EF=3CF.
∵CD=DF+CF=4,∴3CF+CF=4,解得CF=1,∴CE=CF=
1,AE=AC-CE=2.
综上所述,当∠BAD=∠CDE时,AE的长为2或 .
7. 在△ABC中,∠ACB=90°,AC=BC,D为AB上一点.
(1)如图①,H为CD上一动点,过点H作EF⊥CD,交BC于点E,
交AC于点F,若 = ,求 的值;
解:(1)如图①,过点A作AM∥BC,交CD的延长线于
点M,
∴△ADM∽△BDC,∴ = = = ,
∴tan∠ACM= ,∴tan∠HCF=tan∠CEH= ,
∴ = , = ,∴ = .
(2)如图②,点H在CD上,且∠AHD=45°,CH=DH,求 的
值.
解:(2)如图②,过点D作DN⊥AC于点N. 设CH=
DH= DC=x.
∵∠AHD=∠CAD=45°,∠ADH=∠CDA,
∴△ADH∽△CDA,∴AD2=HD·CD=2x2,
∴AD= x,AN=DN= AD=x,∴CN= = = x,∴ = = = .
类型三 构造全等三角形求线段长
在图形中遇到求线段长时,有时通过作垂线或平行线的方法构造
全等三角形,利用全等三角形的性质达到与已知线段长的等量转换,
再结合勾股定理、相似三角形等相关知识求解.
1. 如图,在四边形ABCD中,对角线AC,BD相交于点E,且E为对角
线BD的中点,∠DAE=30°,∠BCE=120°.若CE=1,BC=2,求
AC的长.
解:如图,过点D作DM∥BC,交AC于点M. 易得△DEM≌△BEC
(ASA或AAS),
∴DM=BC=2,ME=CE=1,∠DME=∠BCE=120°,∴∠AMD
=60°.
又∵∠DAE=30°,∴∠ADM=90°,∴AM=2DM=4,∴AC=
AM+MC=4+2=6.
2. 如图,在△ABC中,∠ACB=90°,AC=BC=4,P为△ABC内一
点,连接AP,BP,CP,其中CP的延长线交AB于点E,若∠CBP=
∠PCB=15°,求AP的长.
解:如图,过点A作AM⊥CE于点M,过点B作BN⊥CE,交CE的延长线于点N.
易得△ACM≌△CBN(AAS).设BN=CM=x.∵∠CBP=∠PCB=15°,∴∠BPN=30°,
∴CP=BP=2BN=2x,∴PM=CM=x,∴AM为CP的垂直平分线,∴AP=AC=4.
3. 如图,在△ABC中,∠A=∠ACB,AC=2,点P在边AB上,Q在
BC的延长线上,且PA=QC,连接PQ交AC于点D,PE⊥AC于点
E,求DE的长.
解:如图,过点P作PF∥BC,交AC于点F,
∴∠A=∠ACB=∠AFP,∴PA=PF. 又∵PE⊥AC,∴EF= AF.
∵∠PFD=∠QCD,∠PDF=∠QDC,PF=PA=QC,∴△PDF≌△QDC(AAS),
∴DF=DC,∴DE=EF+DF= AF+ FC= AC= ×2=1.
4. 如图,在△ABC中,∠ACB=90°,AC=BC=4,D为AC的中
点,CH⊥BD于点H,O为AB的中点,连接OH,求OH的长.
解:如图,连接CO,过点O作OE⊥OH,交BD于点E. 易得CO=BO,∠HOC=∠EOB.
∵∠ACO=∠OBC=45°,∠DCH=∠HBC,∴∠OCH=∠OBE,
∴△OCH≌△OBE(ASA),∴OH=OE,CH=BE.
∵CD=2,BC=4,
∴BD= =2 .∵ BD·CH= CD·BC,∴CH=BE= .
又∵BH= = ,∴HE=BH-BE= .
∵△OEH是等腰直角三角形,∴OH= HE=× = .
类型四 利用旋转变换求线段长
当遇到“从一点(O)呈放射状发射出三条线段(OA,OB,
OC),且其中有两条线段相等(OA=OB,OA与OB的夹角为α)”
的几何图形,求某线段长时,往往可以以点O为旋转中心,将以OA
(或OB)为边的一个三角形旋转α度,使其与OB(或OA)重合,构
造出“手拉手模型”,实现线段的等量转换,图形重构.
1. 如图,在△ABC中,∠ABC=45°,AB= ,BC=4,以AC为直
角边作等腰直角三角形ACD,连接BD,求BD的长.
解:如图,将△ABD绕点A顺时针旋转90°得到△AEC,连接BE.
易得△AEC≌△ABD,△ABE为等腰直角三角形,
∴BD=EC,EB= AB= × =3.
∵∠ABC=∠ABE=45°,∴∠EBC=90°,∴BD=EC= = =5.
2. 如图,E为菱形ABCD外一点,∠BEA=∠ABC=60°,AE=3,
BE=5,求DE的长.
解:如图,将△EAD绕点A顺时针旋转120°得到△FAB,连接EF,过点A作AM⊥EF于点M.
易得△FAB≌△EAD,AF=AE,BF=DE,∠EAF=∠BAD=120°,
∴∠AEF=(180°-120°)÷2=30°,∠BEF=∠AEF+∠BEA=90°.
∵AM= AE= ,EM= = ,
∴EF=2EM=3 ,∴DE=BF= =
=2 .
3. 如图,P是正方形ABCD内一点,且点P到点A,B,C的距离分别
为2 , ,4,求正方形ABCD的面积.
解:如图,将△ABP绕点B顺时针旋转90°得到△CBM,连接PM,过点B作BH⊥PM于点H.
∵BP=BM= ,∠PBM=90°,∴PM= BM=2.∵PC=4,PA=MC=2 ,
∴PC2=CM2+PM2,∴∠PMC=90°.∵∠BPM=∠BMP=45°,
∴∠CMB=∠APB=135°,∴∠APB+∠BPM=180°,∴A,P,M三点共线.
∵BH⊥PM,∴PH=HM,∴BH=PH=HM=1,
∴AH=2 +1,
∴AB2=AH2+BH2=(2 +1)2+12=14+4 ,∴
正方形ABCD的面积为14+4 .
4. 如图,B,C为△ADE的边DE上两点,∠BAC=90°,AB=AC.
若∠DAE=135°,BD=2,CE=3,求AB的长.
解:如图,将△ABE绕点A逆时针旋转90°得到
△ACF,连接DF. 易得△ACF≌△ABE,
∴CF=BE,AF=AE,∠ACF=∠ABE. ∵∠BAC
=90°,AB=AC,
∴∠ACF=∠ABE=∠ACB=45°,∴∠DCF=
90°,即△DCF为直角三角形.
∵∠DAE=135°,∠FAE=90°,∴∠DAF=360°
-∠DAE-∠FAE=135°,
∴∠DAE=∠DAF. 又∵AF=AE,AD=AD,
∴△ADE≌△ADF(SAS),
∴DF=DE. 设BC=x,则CF=BE=x+3,DF=DE=x+5,
DC=x+2.
在Rt△FCD中,DF2=DC2+CF2,∴(x+5)2=(x+2)2+
(x+3)2,解得x=2 或x=-2 (舍去).
∴BC=2 ,∴AB= BC= .
5. 如图,在△ABC中,∠ABC=60°,AB=6,BC=10,以AC为边
向外作等边三角形ACD,连接BD,求BD的长.
解:如图,将△ABD绕点A顺时针旋转60°得到△AEC,连接BE.
易得△AEC≌△ABD,△ABE为等边三角形,∴BD=EC,
EB=AB=6,∠EBC=120°.
过点E作EF⊥CB,交CB的延长线于点F(如图),则∠BEF=
∠EBC-∠F=30°,
∴BF= EB=3,EF= =3 ,
∴BD=EC= = =14.
6. [2024·宜宾改编]如图,在△ABC中,AB=3 ,AC=2,以BC为
边作Rt△BCD,BC=BD,点D与点A在BC的两侧,求AD的最大值.
解:如图,将BA绕点B顺时针旋转90°至BE,连接AE,DE.
∵BE=BA,∠ABE=90°,∴AE= AB= ×3 =6.
∵∠DBC=∠EBA=90°,∴∠DBE=∠CBA. 又∵BD=BC,
BE=BA,
∴△DBE≌△CBA(SAS),∴DE=CA=2.
∵在△ADE中,由三角形三边关系可得AD<AE+DE,
∴当A,D,E三点共线时,AD有最大值,
∴AD的最大值为DE+AE=2+6=8.
谢谢观看
同课章节目录
