【专项培优】沪科版数学八年级下册第19章四边形(含答案)
文档属性
| 名称 | 【专项培优】沪科版数学八年级下册第19章四边形(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 16:10:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【专项培优】沪科版数学八年级下册第19章四边形
一、单选题
1.(2023八上·长葛期中)已知正多边形的一个内角是,则这个正多边形的边数是( )
A.九边形 B.八边形 C.七边形 D.六边形
2.(2023八下·长垣期末)关于平行四边形的性质,以下说法不正确的是( )
A.对边相等 B.对角线互相平分
C.对角相等 D.是轴对称图形
3.(2024九下·天河月考)如图,在中,AC,BD相交于点O,若,则线段AO的长为( )
A.3 B.4 C.5 D.16
4.(2023八下·萝北期末)如图,过平行四边形对角线的交点O,交于E,交于F,若平行四边形的周长为36,,则四边形的周长为( )
A.24 B.26 C.28 D.20
5.(2024九上·胶州月考)下列说法正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
二、判断题
6.(2023七上·南宁开学考)两个等底等高的三角形拼成的一定是平行四边形 .
7.(2023八上·墨玉月考)六边形的一个顶点可以引出3条对角线
8.(2023七上·市中区开学考)边长是4分米的正方形,它的周长与面积相等( )
三、填空题
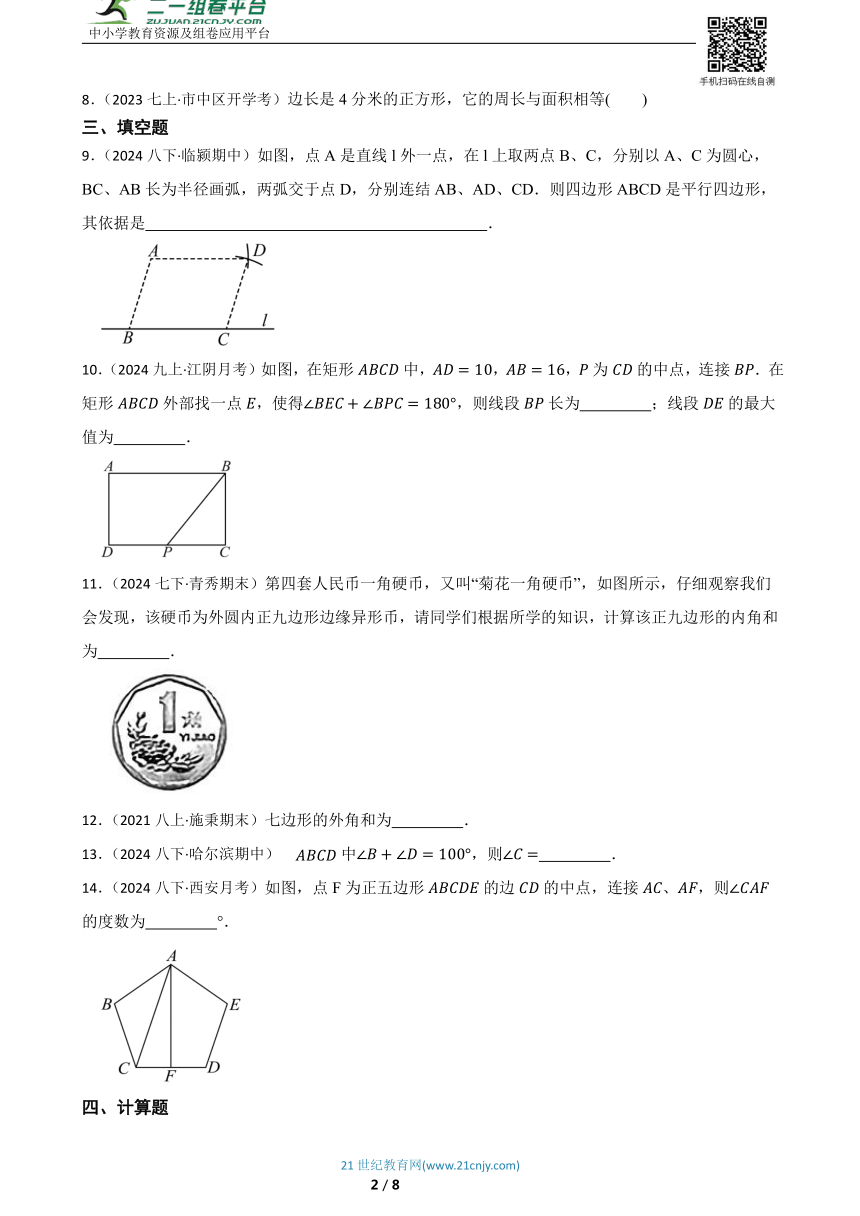
9.(2024八下·临颍期中)如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD.则四边形ABCD是平行四边形,其依据是 .
10.(2024九上·江阴月考)如图,在矩形中,,,为的中点,连接.在矩形外部找一点,使得,则线段长为 ;线段的最大值为 .
11.(2024七下·青秀期末)第四套人民币一角硬币,又叫“菊花一角硬币”,如图所示,仔细观察我们会发现,该硬币为外圆内正九边形边缘异形币,请同学们根据所学的知识,计算该正九边形的内角和为 .
12.(2021八上·施秉期末)七边形的外角和为 .
13.(2024八下·哈尔滨期中)中,则 .
14.(2024八下·西安月考)如图,点F为正五边形的边的中点,连接、,则的度数为 °.
四、计算题
15.(2024八下·合肥期末)如图,在正方形网格中,的顶点在边长为1的小正方形的顶点(格点)上,若坐标平面内的点的坐标分别为,.
(1)通过计算判断的形状,
(2)若要使以四个点为顶点的四边形是平行四边形,则满足条件的D点的坐标是 .
16.(2024八下·桂阳期中)列式计算:求图中x的值.
五、解答题
17.(2024八上·广州期中)一个多边形的内角和比它的外角和多900°,求这个多边形的边数.
18.(2023八下·江海期中)如图,一块长方形场地的长与宽之比为,于点E,于点F,连结.现计划在四边形区域内种植花草,求四边形与长方形的面积之比.
六、综合题
19.(2021八上·台安月考)一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1) 求这个多边形是几边形;
(2) 求这个多边形的内角和
20.(2024八上·玉州期中)一个多边形的内角和比其外角和的3倍多,求这个多边形的边数.
21.如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:
(1)AD∥BC,AB∥CD;
(2)AD=BC,AB=CD.
七、实践探究题
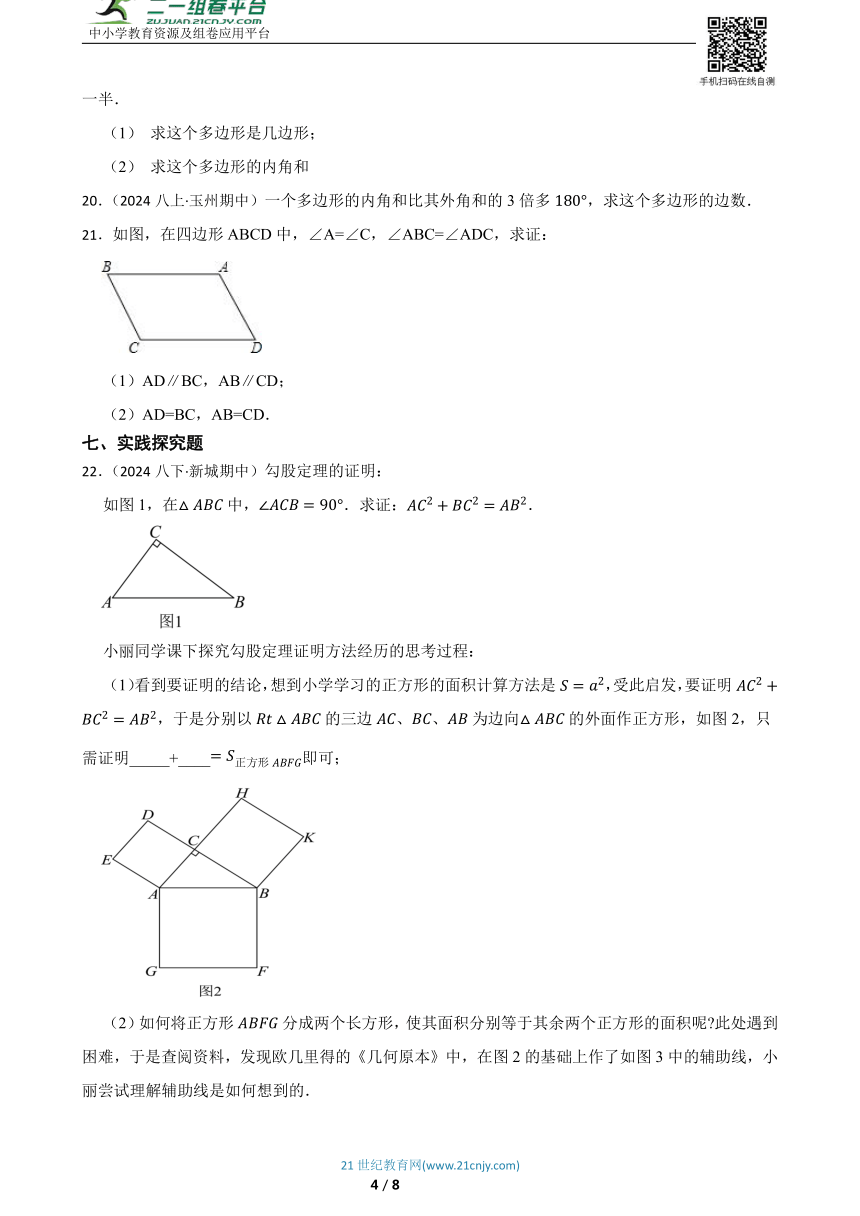
22.(2024八下·新城期中)勾股定理的证明:
如图1,在中,.求证:.
小丽同学课下探究勾股定理证明方法经历的思考过程:
(1)看到要证明的结论,想到小学学习的正方形的面积计算方法是,受此启发,要证明,于是分别以的三边、、为边向的外面作正方形,如图2,只需证明_____+____即可;
(2)如何将正方形分成两个长方形,使其面积分别等于其余两个正方形的面积呢 此处遇到困难,于是查阅资料,发现欧几里得的《几何原本》中,在图2的基础上作了如图3中的辅助线,小丽尝试理解辅助线是如何想到的.
①首先过点C作边的垂线,垂足为点M,交于点N,就实现将正方形分成两个长方形的目的,只需证明, _______;
②要想建立正方形和长方形面积的关系,只能将其分别建立与和的面积关系,易得,_____,而( )(填推理依据),于是、同理将正方形的面积转化为另一长方形的面积,小丽通过体验勾股定理的探索过程,发现利用面积证法将未知问题逐步转化为已知问题.
答案解析部分
1.【答案】B
【知识点】多边形内角与外角
2.【答案】D
【知识点】平行四边形的性质
3.【答案】B
【知识点】平行四边形的性质
4.【答案】A
【知识点】平行四边形的性质
5.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】
【知识点】平行四边形的判定
7.【答案】正确
【知识点】多边形的对角线
8.【答案】错误
【知识点】正方形的性质
9.【答案】两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质
10.【答案】;
【知识点】勾股定理;矩形的性质;三角形的中位线定理
11.【答案】
【知识点】多边形内角与外角
12.【答案】360°
【知识点】多边形内角与外角
13.【答案】
【知识点】平行四边形的性质
14.【答案】18
【知识点】等腰三角形的性质;多边形内角与外角;三角形全等的判定-SAS
15.【答案】(1)直角三角形
(2)或或
【知识点】勾股定理的逆定理;平行四边形的判定;坐标与图形变化﹣平移
16.【答案】100
【知识点】多边形内角与外角
17.【答案】这个多边形的边数是9
【知识点】多边形内角与外角
18.【答案】
【知识点】二次根式的乘除法;平行四边形的判定与性质;矩形的性质
19.【答案】(1) 设多边形的每一个内角为x,则每一个外角为 x,
由题意得,x+ x=180°,
解得,x=120°,
x=60°,
这个多边形的边数为: =6,
答:这个多边形是六边形
(2)解:由(1)知,该多边形是六边形,∴内角和=(6﹣2)×180°=720°
答:这个多边形的内角和为720°。
【知识点】多边形内角与外角
20.【答案】解:∵任意多边形的外角和的度数为360°,
∴这个多边形的内角和度数为:,
设这个多边形的边数是n,依题意得,,
解得:n=9.
∴这个多边形的边数是9.
【知识点】多边形内角与外角
21.【答案】(1)证明:如图,∵在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,
∴四边形ABCD是平行四边形.
由“四边形ABCD是平行四边形”得到:AD∥BC,AB∥CD
(2)证明:由“四边形ABCD是平行四边形”得到:AD=BC,AB=CD
【知识点】平行四边形的判定与性质
22.【答案】(1),
(2)①;②,图形全等
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
1 / 8
【专项培优】沪科版数学八年级下册第19章四边形
一、单选题
1.(2023八上·长葛期中)已知正多边形的一个内角是,则这个正多边形的边数是( )
A.九边形 B.八边形 C.七边形 D.六边形
2.(2023八下·长垣期末)关于平行四边形的性质,以下说法不正确的是( )
A.对边相等 B.对角线互相平分
C.对角相等 D.是轴对称图形
3.(2024九下·天河月考)如图,在中,AC,BD相交于点O,若,则线段AO的长为( )
A.3 B.4 C.5 D.16
4.(2023八下·萝北期末)如图,过平行四边形对角线的交点O,交于E,交于F,若平行四边形的周长为36,,则四边形的周长为( )
A.24 B.26 C.28 D.20
5.(2024九上·胶州月考)下列说法正确的是( )
A.对角线互相垂直且相等的四边形是正方形
B.对角线互相平分的四边形是菱形
C.对角线互相垂直的四边形是平行四边形
D.对角线相等的平行四边形是矩形
二、判断题
6.(2023七上·南宁开学考)两个等底等高的三角形拼成的一定是平行四边形 .
7.(2023八上·墨玉月考)六边形的一个顶点可以引出3条对角线
8.(2023七上·市中区开学考)边长是4分米的正方形,它的周长与面积相等( )
三、填空题
9.(2024八下·临颍期中)如图,点A是直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连结AB、AD、CD.则四边形ABCD是平行四边形,其依据是 .
10.(2024九上·江阴月考)如图,在矩形中,,,为的中点,连接.在矩形外部找一点,使得,则线段长为 ;线段的最大值为 .
11.(2024七下·青秀期末)第四套人民币一角硬币,又叫“菊花一角硬币”,如图所示,仔细观察我们会发现,该硬币为外圆内正九边形边缘异形币,请同学们根据所学的知识,计算该正九边形的内角和为 .
12.(2021八上·施秉期末)七边形的外角和为 .
13.(2024八下·哈尔滨期中)中,则 .
14.(2024八下·西安月考)如图,点F为正五边形的边的中点,连接、,则的度数为 °.
四、计算题
15.(2024八下·合肥期末)如图,在正方形网格中,的顶点在边长为1的小正方形的顶点(格点)上,若坐标平面内的点的坐标分别为,.
(1)通过计算判断的形状,
(2)若要使以四个点为顶点的四边形是平行四边形,则满足条件的D点的坐标是 .
16.(2024八下·桂阳期中)列式计算:求图中x的值.
五、解答题
17.(2024八上·广州期中)一个多边形的内角和比它的外角和多900°,求这个多边形的边数.
18.(2023八下·江海期中)如图,一块长方形场地的长与宽之比为,于点E,于点F,连结.现计划在四边形区域内种植花草,求四边形与长方形的面积之比.
六、综合题
19.(2021八上·台安月考)一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1) 求这个多边形是几边形;
(2) 求这个多边形的内角和
20.(2024八上·玉州期中)一个多边形的内角和比其外角和的3倍多,求这个多边形的边数.
21.如图,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:
(1)AD∥BC,AB∥CD;
(2)AD=BC,AB=CD.
七、实践探究题
22.(2024八下·新城期中)勾股定理的证明:
如图1,在中,.求证:.
小丽同学课下探究勾股定理证明方法经历的思考过程:
(1)看到要证明的结论,想到小学学习的正方形的面积计算方法是,受此启发,要证明,于是分别以的三边、、为边向的外面作正方形,如图2,只需证明_____+____即可;
(2)如何将正方形分成两个长方形,使其面积分别等于其余两个正方形的面积呢 此处遇到困难,于是查阅资料,发现欧几里得的《几何原本》中,在图2的基础上作了如图3中的辅助线,小丽尝试理解辅助线是如何想到的.
①首先过点C作边的垂线,垂足为点M,交于点N,就实现将正方形分成两个长方形的目的,只需证明, _______;
②要想建立正方形和长方形面积的关系,只能将其分别建立与和的面积关系,易得,_____,而( )(填推理依据),于是、同理将正方形的面积转化为另一长方形的面积,小丽通过体验勾股定理的探索过程,发现利用面积证法将未知问题逐步转化为已知问题.
答案解析部分
1.【答案】B
【知识点】多边形内角与外角
2.【答案】D
【知识点】平行四边形的性质
3.【答案】B
【知识点】平行四边形的性质
4.【答案】A
【知识点】平行四边形的性质
5.【答案】D
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
6.【答案】
【知识点】平行四边形的判定
7.【答案】正确
【知识点】多边形的对角线
8.【答案】错误
【知识点】正方形的性质
9.【答案】两组对边分别相等的四边形是平行四边形.
【知识点】平行四边形的判定与性质
10.【答案】;
【知识点】勾股定理;矩形的性质;三角形的中位线定理
11.【答案】
【知识点】多边形内角与外角
12.【答案】360°
【知识点】多边形内角与外角
13.【答案】
【知识点】平行四边形的性质
14.【答案】18
【知识点】等腰三角形的性质;多边形内角与外角;三角形全等的判定-SAS
15.【答案】(1)直角三角形
(2)或或
【知识点】勾股定理的逆定理;平行四边形的判定;坐标与图形变化﹣平移
16.【答案】100
【知识点】多边形内角与外角
17.【答案】这个多边形的边数是9
【知识点】多边形内角与外角
18.【答案】
【知识点】二次根式的乘除法;平行四边形的判定与性质;矩形的性质
19.【答案】(1) 设多边形的每一个内角为x,则每一个外角为 x,
由题意得,x+ x=180°,
解得,x=120°,
x=60°,
这个多边形的边数为: =6,
答:这个多边形是六边形
(2)解:由(1)知,该多边形是六边形,∴内角和=(6﹣2)×180°=720°
答:这个多边形的内角和为720°。
【知识点】多边形内角与外角
20.【答案】解:∵任意多边形的外角和的度数为360°,
∴这个多边形的内角和度数为:,
设这个多边形的边数是n,依题意得,,
解得:n=9.
∴这个多边形的边数是9.
【知识点】多边形内角与外角
21.【答案】(1)证明:如图,∵在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,
∴四边形ABCD是平行四边形.
由“四边形ABCD是平行四边形”得到:AD∥BC,AB∥CD
(2)证明:由“四边形ABCD是平行四边形”得到:AD=BC,AB=CD
【知识点】平行四边形的判定与性质
22.【答案】(1),
(2)①;②,图形全等
【知识点】勾股定理;正方形的性质;三角形全等的判定-SAS
21世纪教育网(www.21cnjy.com)
1 / 8
