3.１圆的对称性(第一课时) 学案

3.１圆的对称性(第一课时) 学案
〖学习目标〗1．经历探索圆的对称性及有关性质的过程.
2．理解圆的对称性及有关性质.
3．会垂径定理解决有关问题.
〖学习过程〗
一.知识回顾:
（1）什么是轴对称图形？
（2）我们采用什么方法研究轴对称图形？
二、探究新知:
活动一 操作、思考
在圆形纸片上任意画一条直径.
沿直径将圆形纸片对折，你能发现什么？请将你的发现写下来：
________________________________________________________________________.
活动二 思考、探索
如图，CD是⊙O的弦，画直径AB⊥CD，垂足为P；将圆形纸片沿AB对折.
通过折叠活动，你发现了什么？
__________________________________________________________________.
请试一试证明！
垂径定理：_________________________________________________________。
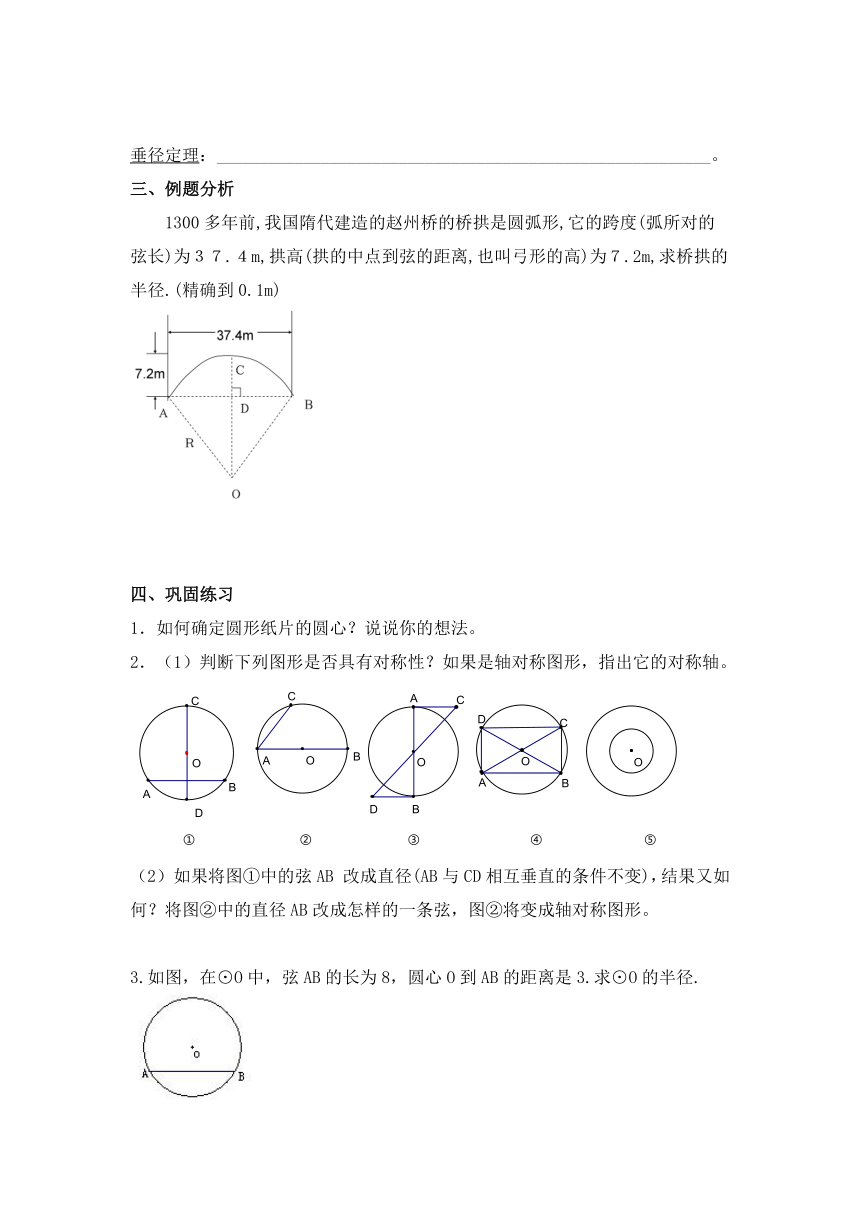
三、例题分析
1300多年前,我国隋代建造的赵州桥的桥拱 ( http: / / www.21cnjy.com )是圆弧形,它的跨度(弧所对的弦长)为３７.４m,拱高(拱的中点到弦的距离,也叫弓形的高)为７.2m,求桥拱的半径.(精确到0.1m)
( http: / / www.21cnjy.com / )
四、巩固练习
1．如何确定圆形纸片的圆心？说说你的想法。
2．（1）判断下列图形是否具有对称性？如果是轴对称图形，指出它的对称轴。
( http: / / www.21cnjy.com / )
（2）如果将图①中的弦AB 改成直径(AB ( http: / / www.21cnjy.com )与CD相互垂直的条件不变)，结果又如何？将图②中的直径AB改成怎样的一条弦，图②将变成轴对称图形。
3.如图，在⊙O中，弦AB的长为8，圆心O到AB的距离是3.求⊙O的半径.
( http: / / www.21cnjy.com / )
4.如图，在⊙O中，直径AB=10，弦CD⊥AB，垂足为E，OE=3，求弦CD的长.
( http: / / www.21cnjy.com / )
五、拓展延伸
１.如图，过⊙O内一点P，作⊙O的弦AB，使它以点P为中点。
( http: / / www.21cnjy.com / )
２.如图，⊙O的直径是10，弦AB的长为8，P是AB上的一个动点，求OP的求值范围。
( http: / / www.21cnjy.com / )
３.如图，OA=OB，AB交⊙O与点C、D，AC与BD是否相等？为什么？
( http: / / www.21cnjy.com / )
４.在直径为650mm的圆柱形油罐内装进一些油后，其横截面如图，若油面宽AB=600mm，求油的最大深度。
( http: / / www.21cnjy.com / )
六、回顾反思　交流收获
七.达标测试
如图，以点O为圆心的两个同心圆中，大圆的弦AB交小圆于点C、D.AC与BD相等吗？为什么？
拓展思考：如图，AB、CD是⊙O的两条平行弦，AC与BD相等吗？为什么？
( http: / / www.21cnjy.com / )
八.作业
习题４.１Ａ组　１、２、３题