【专项培优】北师大版数学八年级下册第一章三角形的证明(含答案)
文档属性
| 名称 | 【专项培优】北师大版数学八年级下册第一章三角形的证明(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 898.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 16:18:26 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【专项培优】北师大版数学八年级下册第一章三角形的证明
一、单选题
1.(2020八上·盐田期末)下列命题是真命题的为( )
A.若两角的两边分别平行,则这两角相等
B.若两实数相等,则它们的绝对值相等
C.对应角相等的两个三角形是全等三角形
D.锐角三角形是等边三角形
2.(2023七上·利津期末)已知一个三角形的三边长分别为a、b、c,且它们满足,则该三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.(2024九下·河西模拟)如图,中,,,分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;作直线,与边于点E,则的长为( )
A.3 B.4 C.5 D.6
4.(2023八上·青羊期中)由线段a,b,c组成的三角形不是直角三角形的是( )
A. B.
C.,, D.
5.(2023八下·金安期末)给出下列四个命题中,其中是假命题的是( )
A.在中,如果满足,那么
B.在中,如果两直角边长分别为6和8,那么斜边长为10
C.在中,如果,那么是直角三角形
D.在中,如果,那么是直角三角形
二、判断题
6.(2022七上·丰润开学考)判断题:一个直角三角形中,有一个锐角是,另一个锐角是.
三、填空题
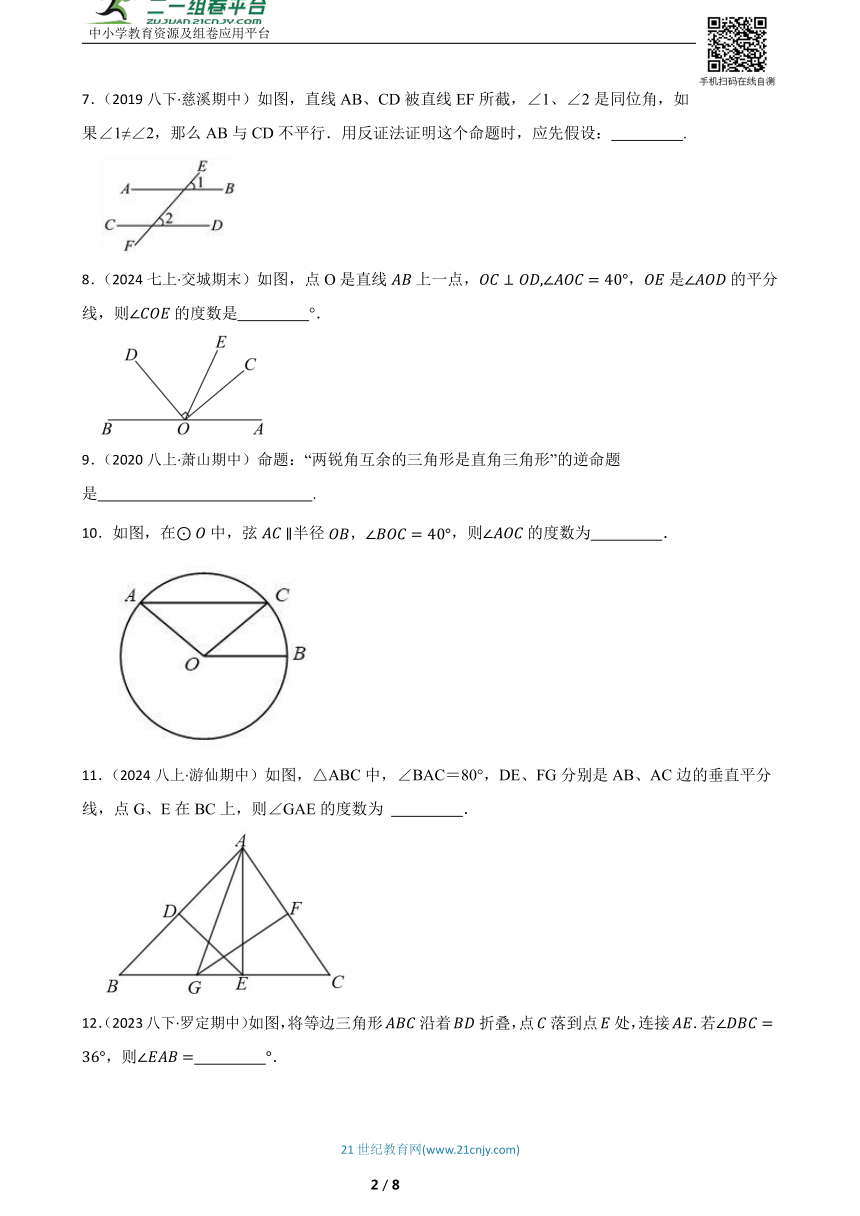
7.(2019八下·慈溪期中)如图,直线AB、CD被直线EF所截,∠1、∠2是同位角,如果∠1≠∠2,那么AB与CD不平行.用反证法证明这个命题时,应先假设: .
8.(2024七上·交城期末)如图,点O是直线上一点,,是的平分线,则的度数是 °.
9.(2020八上·萧山期中)命题:“两锐角互余的三角形是直角三角形”的逆命题是 .
10.如图,在中,弦半径,则的度数为 .
11.(2024八上·游仙期中)如图,△ABC中,∠BAC=80°,DE、FG分别是AB、AC边的垂直平分线,点G、E在BC上,则∠GAE的度数为 .
12.(2023八下·罗定期中)如图,将等边三角形沿着折叠,点落到点处,连接.若,则 .
四、计算题
13.(2024八上·武功期末)如图,在中,,,的外角的平分线交的延长线于点,交的延长线于点.求和的度数.
14.(2024八上·下陆月考)如图,在中,为的平分线,交于点.
(1)求的度数;
(2)请你画出的中线,再找出的中点,连接.若,求的面积.
五、解答题
15.(2017八下·文安期末)一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
16.(2024七下·金溪期中)中,是的角平分线,E为上一点,于F,,求的度数.
六、综合题
17.(2017八下·广州期中)如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD= c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
18.(2024八上·南安期末)如图是某区域仓储配送中心的部分平面图,A区为商品入库区,B区,C区是配送中心区.已知B,C两个配送中心区相距250m,A,B区相距200m,A,C区相距150m,为了方便商品从库区分拣传送至配送中心,现有两种搭建传送带的方案.
甲方案:从A区直接搭建两条传送带分别到B区,C区;
乙方案:在B区,C区之间搭建一条传送带,再从A区搭建一条垂直于BC的传送带,两条传送带的连接处为中转站D区(接缝忽略不计).
(1)请判断此平面图形的形状(要求写出推理过程)
(2)甲,乙两种方案中,哪一种方案所搭建的传送带较短?请通过计算说明.
19.(2019八上·泰州月考)如图, ,垂足为 . 如果 ,
(1)直接写出 , ;
(2) 是直角三角形吗?证明你的结论.
七、实践探究题
20.(2024八上·绍兴竞赛)【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】B
【知识点】平行线的性质;三角形全等的判定;等边三角形的判定;实数的绝对值;真命题与假命题
2.【答案】B
【知识点】勾股定理的逆定理
3.【答案】A
【知识点】三角形的外角性质;线段垂直平分线的性质;勾股定理
4.【答案】D
【知识点】三角形内角和定理;勾股定理的逆定理
5.【答案】A
【知识点】三角形内角和定理;勾股定理;勾股定理的逆定理;真命题与假命题
6.【答案】正确
【知识点】直角三角形的性质
7.【答案】AB∥CD
【知识点】反证法
8.【答案】25
【知识点】垂线的概念;角平分线的性质
9.【答案】直角三角形的两锐角互余
【知识点】逆命题
10.【答案】100°
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质
11.【答案】20°
【知识点】三角形内角和定理;线段垂直平分线的性质
12.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的性质
13.【答案】,.
【知识点】三角形的外角性质;角平分线的性质;同位角的概念
14.【答案】(1)
(2)
【知识点】三角形的角平分线、中线和高;角平分线的性质
15.【答案】解:∵42+32=52,52+122=132,
即AB2+BC2=AC2,故∠B=90°,
同理,∠ACD=90°
∴S四边形ABCD=S△ABC+S△ACD
= ×3×4+ ×5×12
=6+30
=36.
【知识点】勾股定理的逆定理
16.【答案】
【知识点】三角形内角和定理;直角三角形的性质
17.【答案】(1)证明:在Rt△ABC和Rt△DCE中,
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°﹣(∠BAC+∠AEF)=90°.
∴DE⊥AB
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE= a2+ b2+ cx,
∵ ,
∴ .
∴a2+b2=c2
【知识点】全等三角形的判定与性质;勾股定理的证明
18.【答案】(1)是直角三角形;
(2)甲方案所搭建的传送带较短.
【知识点】勾股定理的逆定理
19.【答案】(1)5;10
(2)解:∵AC= ;AB=2 ,BC=CD+BD=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网(www.21cnjy.com)
8 / 8
【专项培优】北师大版数学八年级下册第一章三角形的证明
一、单选题
1.(2020八上·盐田期末)下列命题是真命题的为( )
A.若两角的两边分别平行,则这两角相等
B.若两实数相等,则它们的绝对值相等
C.对应角相等的两个三角形是全等三角形
D.锐角三角形是等边三角形
2.(2023七上·利津期末)已知一个三角形的三边长分别为a、b、c,且它们满足,则该三角形的形状为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.(2024九下·河西模拟)如图,中,,,分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;作直线,与边于点E,则的长为( )
A.3 B.4 C.5 D.6
4.(2023八上·青羊期中)由线段a,b,c组成的三角形不是直角三角形的是( )
A. B.
C.,, D.
5.(2023八下·金安期末)给出下列四个命题中,其中是假命题的是( )
A.在中,如果满足,那么
B.在中,如果两直角边长分别为6和8,那么斜边长为10
C.在中,如果,那么是直角三角形
D.在中,如果,那么是直角三角形
二、判断题
6.(2022七上·丰润开学考)判断题:一个直角三角形中,有一个锐角是,另一个锐角是.
三、填空题
7.(2019八下·慈溪期中)如图,直线AB、CD被直线EF所截,∠1、∠2是同位角,如果∠1≠∠2,那么AB与CD不平行.用反证法证明这个命题时,应先假设: .
8.(2024七上·交城期末)如图,点O是直线上一点,,是的平分线,则的度数是 °.
9.(2020八上·萧山期中)命题:“两锐角互余的三角形是直角三角形”的逆命题是 .
10.如图,在中,弦半径,则的度数为 .
11.(2024八上·游仙期中)如图,△ABC中,∠BAC=80°,DE、FG分别是AB、AC边的垂直平分线,点G、E在BC上,则∠GAE的度数为 .
12.(2023八下·罗定期中)如图,将等边三角形沿着折叠,点落到点处,连接.若,则 .
四、计算题
13.(2024八上·武功期末)如图,在中,,,的外角的平分线交的延长线于点,交的延长线于点.求和的度数.
14.(2024八上·下陆月考)如图,在中,为的平分线,交于点.
(1)求的度数;
(2)请你画出的中线,再找出的中点,连接.若,求的面积.
五、解答题
15.(2017八下·文安期末)一个零件的形状如图所示,工人师傅按规定做得AB=3,BC=4,AC=5,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?
16.(2024七下·金溪期中)中,是的角平分线,E为上一点,于F,,求的度数.
六、综合题
17.(2017八下·广州期中)如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F.
(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD= c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
18.(2024八上·南安期末)如图是某区域仓储配送中心的部分平面图,A区为商品入库区,B区,C区是配送中心区.已知B,C两个配送中心区相距250m,A,B区相距200m,A,C区相距150m,为了方便商品从库区分拣传送至配送中心,现有两种搭建传送带的方案.
甲方案:从A区直接搭建两条传送带分别到B区,C区;
乙方案:在B区,C区之间搭建一条传送带,再从A区搭建一条垂直于BC的传送带,两条传送带的连接处为中转站D区(接缝忽略不计).
(1)请判断此平面图形的形状(要求写出推理过程)
(2)甲,乙两种方案中,哪一种方案所搭建的传送带较短?请通过计算说明.
19.(2019八上·泰州月考)如图, ,垂足为 . 如果 ,
(1)直接写出 , ;
(2) 是直角三角形吗?证明你的结论.
七、实践探究题
20.(2024八上·绍兴竞赛)【概念学习】
规定①:如果一个三角形的三个角分别等于另一个三角形的三个角,那么称这两个三角形互为“形似三角形”.
规定②:从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原来三角形是“形似三角形”,我们把这条线段叫做这个三角形的“等腰分割线”.
(1)【概念理解】
如图1,在△ABC中,∠A=36°,AB=AC,CD平分∠ACB,则△CBD与△ABC (填“是”或“不是”)互为“形似三角形”.
(2)如图2,在△ABC中,CD平分∠ACB,∠A=36°,∠B=48°.求证:CD为△ABC的等腰分割线;
(3)【概念应用】
在△ABC中,∠A=45°,CD是△ABC的等腰分割线,直接写出∠ACB的度数.
答案解析部分
1.【答案】B
【知识点】平行线的性质;三角形全等的判定;等边三角形的判定;实数的绝对值;真命题与假命题
2.【答案】B
【知识点】勾股定理的逆定理
3.【答案】A
【知识点】三角形的外角性质;线段垂直平分线的性质;勾股定理
4.【答案】D
【知识点】三角形内角和定理;勾股定理的逆定理
5.【答案】A
【知识点】三角形内角和定理;勾股定理;勾股定理的逆定理;真命题与假命题
6.【答案】正确
【知识点】直角三角形的性质
7.【答案】AB∥CD
【知识点】反证法
8.【答案】25
【知识点】垂线的概念;角平分线的性质
9.【答案】直角三角形的两锐角互余
【知识点】逆命题
10.【答案】100°
【知识点】平行线的性质;三角形内角和定理;等腰三角形的性质
11.【答案】20°
【知识点】三角形内角和定理;线段垂直平分线的性质
12.【答案】
【知识点】三角形内角和定理;等腰三角形的性质;等边三角形的性质
13.【答案】,.
【知识点】三角形的外角性质;角平分线的性质;同位角的概念
14.【答案】(1)
(2)
【知识点】三角形的角平分线、中线和高;角平分线的性质
15.【答案】解:∵42+32=52,52+122=132,
即AB2+BC2=AC2,故∠B=90°,
同理,∠ACD=90°
∴S四边形ABCD=S△ABC+S△ACD
= ×3×4+ ×5×12
=6+30
=36.
【知识点】勾股定理的逆定理
16.【答案】
【知识点】三角形内角和定理;直角三角形的性质
17.【答案】(1)证明:在Rt△ABC和Rt△DCE中,
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°﹣(∠BAC+∠AEF)=90°.
∴DE⊥AB
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE= a2+ b2+ cx,
∵ ,
∴ .
∴a2+b2=c2
【知识点】全等三角形的判定与性质;勾股定理的证明
18.【答案】(1)是直角三角形;
(2)甲方案所搭建的传送带较短.
【知识点】勾股定理的逆定理
19.【答案】(1)5;10
(2)解:∵AC= ;AB=2 ,BC=CD+BD=5,
∴AC2+AB2=BC2,
∴△ABC是直角三角形
【知识点】勾股定理;勾股定理的逆定理
20.【答案】(1)是
(2)解:∵∠A=36°,∠B=48°,
∴∠ACB=180°-36°-48°=96°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=∠ACB=48°,
∴∠BCD=∠B=∠ACD,
∴△BCD是等腰三角形,
∴∠ADC=∠BCD+∠B=96°,
在△ABC和△ACD中,
∠A=∠A,∠B=∠ACD,∠ACB=∠ADC,
∴△ABC与△ACD互为“形似三角形”
∴CD为△ABC的等腰分割线.
(3)解:105°或112.5°
【知识点】角的运算;三角形内角和定理;等腰三角形的性质
21世纪教育网(www.21cnjy.com)
8 / 8
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
