3.3圆周角(第二课时) 学案(无答案)
文档属性
| 名称 | 3.3圆周角(第二课时) 学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 95.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-28 19:59:18 | ||
图片预览

文档简介
3.3圆周角(第二课时) 学案
学习目标:
1、掌握圆周角定理,并会熟练运用这些知识进行有关的计算和证明;
2、进一步培养观察、分析及解决问题的能力及逻辑推理能力;
3、培养添加辅助线的能力和思维的广阔性。
学习过程:
一、知识回顾
1、我们学习过哪些与圆有关的角?它们之间有什么关系?
2、画一个圆,以B、C为弧的端点能画多少个圆周角?它们有什么关系?
二、探究新知
活动一:
请画出弧AB所对的圆心角以及圆周角
活动二:量一量
量出上图同一个圆中弧AB所对的圆心角以及圆周角的度数
活动三:归纳总结
同一条弧所对的周角和圆心角存在怎样的大小关系?
结论:______________________________
活动四:证明结论
已知:∠BOA,∠BCA分别是同一条弧所对的圆周角和圆心角
求证:∠BCA=∠BOA
(1).首先考虑一种特殊情况:
当圆心(o)在圆周角(∠ACB)的一边(AC)上时
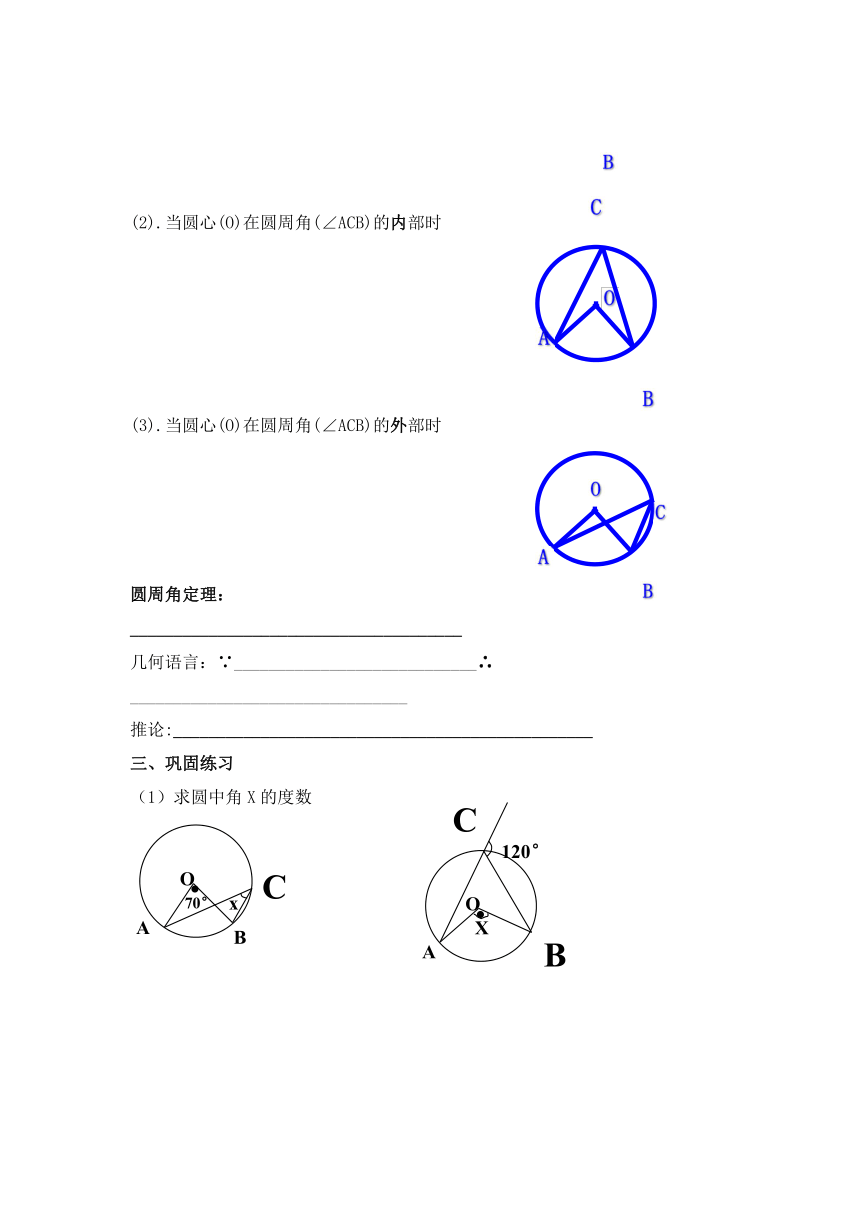
(2).当圆心(O)在圆周角(∠ACB)的内部时
(3).当圆心(O)在圆周角(∠ACB)的外部时
圆周角定理:______________________________________
几何语言:∵____________________________∴________________________________
推论:________________________________________________
三、巩固练习
(1)求圆中角X的度数
(2)如图,圆心角∠AOB=100°,则∠ACB=__ _。
(3)半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .
四、举一反三
变式1:已知:如图,四边形ABCD的四个顶点在⊙O上,∠A=100°,点E在BC的延长线上,求∠DCE的度数。
变式2:如图, B是弧AC上的一点,∠AOC=n°,求∠ABC的度数 。
变式3:如图,在⊙O中,∠AOC=150°,∠ACB=35°,求∠BAC的度数。
五、小结整理
六达标检测
1、如图,AB是⊙O的直径,CD⊥AB,P是CD上的任意一点(不与点C、D重合),∠APC与∠APD相等吗?为什么?
2、如图,AB是⊙O的直径,CD是⊙O的弦,AB=6, ∠DCB=30°,求弦BD的长。
七作业:
习题4.3A组 3、4、5题
学习目标:
1、掌握圆周角定理,并会熟练运用这些知识进行有关的计算和证明;
2、进一步培养观察、分析及解决问题的能力及逻辑推理能力;
3、培养添加辅助线的能力和思维的广阔性。
学习过程:
一、知识回顾
1、我们学习过哪些与圆有关的角?它们之间有什么关系?
2、画一个圆,以B、C为弧的端点能画多少个圆周角?它们有什么关系?
二、探究新知
活动一:
请画出弧AB所对的圆心角以及圆周角
活动二:量一量
量出上图同一个圆中弧AB所对的圆心角以及圆周角的度数
活动三:归纳总结
同一条弧所对的周角和圆心角存在怎样的大小关系?
结论:______________________________
活动四:证明结论
已知:∠BOA,∠BCA分别是同一条弧所对的圆周角和圆心角
求证:∠BCA=∠BOA
(1).首先考虑一种特殊情况:
当圆心(o)在圆周角(∠ACB)的一边(AC)上时
(2).当圆心(O)在圆周角(∠ACB)的内部时
(3).当圆心(O)在圆周角(∠ACB)的外部时
圆周角定理:______________________________________
几何语言:∵____________________________∴________________________________
推论:________________________________________________
三、巩固练习
(1)求圆中角X的度数
(2)如图,圆心角∠AOB=100°,则∠ACB=__ _。
(3)半径为R的圆中,有一弦分圆周成1:2两部分,则弦所对的圆周角的度数是 .
四、举一反三
变式1:已知:如图,四边形ABCD的四个顶点在⊙O上,∠A=100°,点E在BC的延长线上,求∠DCE的度数。
变式2:如图, B是弧AC上的一点,∠AOC=n°,求∠ABC的度数 。
变式3:如图,在⊙O中,∠AOC=150°,∠ACB=35°,求∠BAC的度数。
五、小结整理
六达标检测
1、如图,AB是⊙O的直径,CD⊥AB,P是CD上的任意一点(不与点C、D重合),∠APC与∠APD相等吗?为什么?
2、如图,AB是⊙O的直径,CD是⊙O的弦,AB=6, ∠DCB=30°,求弦BD的长。
七作业:
习题4.3A组 3、4、5题
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
