18.1.1平行四边形的性质 第1课时平行四边形的边、角的性质(共39张PPT)人教版数学八年级下册
文档属性
| 名称 | 18.1.1平行四边形的性质 第1课时平行四边形的边、角的性质(共39张PPT)人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览







文档简介
(共39张PPT)
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角的性质
1. 平行四边形的定义
两组对边 的四边形叫做平行四边形.平行
四边形用符号“ ”表示.
分别平行
(2)已知:如图,在 ABCD中,∠BAD的平分线交
CD于点E,∠ABC的平分线交CD于点F.
结论:①AD=DE,CF=CB,DE=CF;
②AE⊥BF.
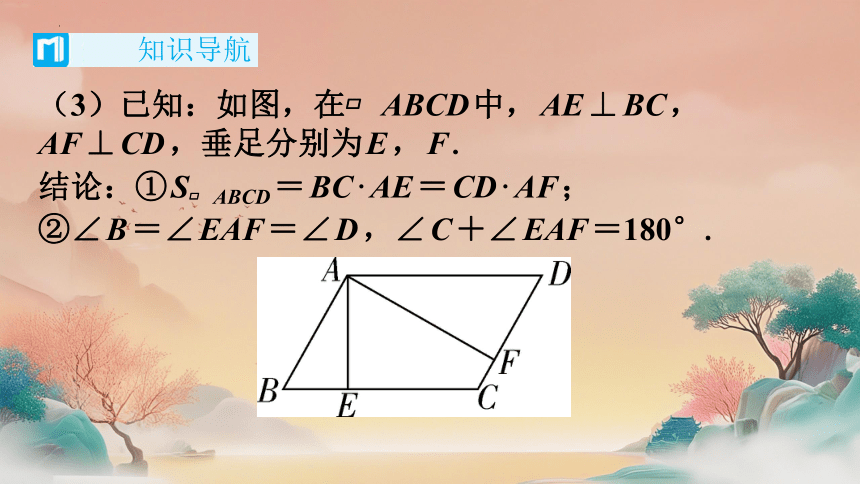
(3)已知:如图,在 ABCD中,AE⊥BC,
AF⊥CD,垂足分别为E,F.
结论:①S ABCD=BC·AE=CD·AF;
②∠B=∠EAF=∠D,∠C+∠EAF=180°.
题型一平行四边形的边、角的性质的应用
(1)平行四边形ABCD中,
∠A∶∠B∶∠C∶∠D的值可以是( B )
A. 1∶2∶3∶4 B. 5∶6∶5∶6
C. 2∶4∶4∶5 D. 4∶4∶3∶3
B
(2)如图,在 ABCD中,AE⊥CD,若∠B=
60°,则∠DAE的度数是 °.
30
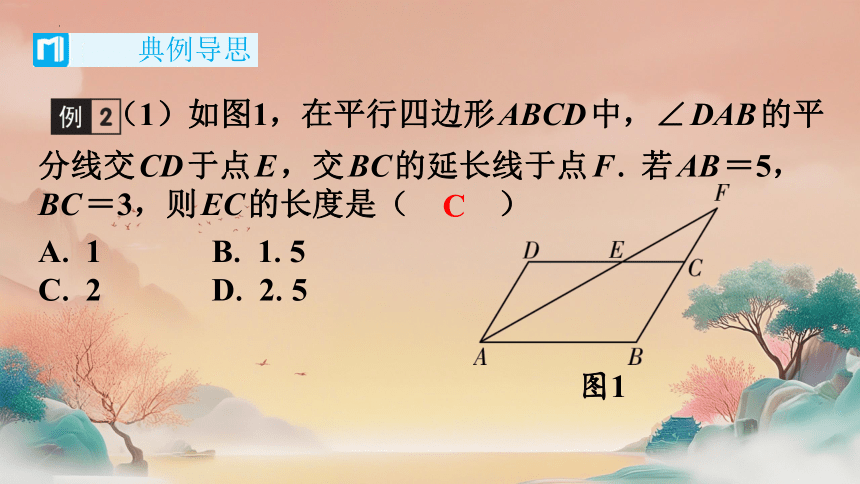
(1)如图1,在平行四边形ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点F. 若AB=5,BC=3,则EC的长度是( C )
C
A. 1 B. 1.5
C. 2 D. 2.5
图1
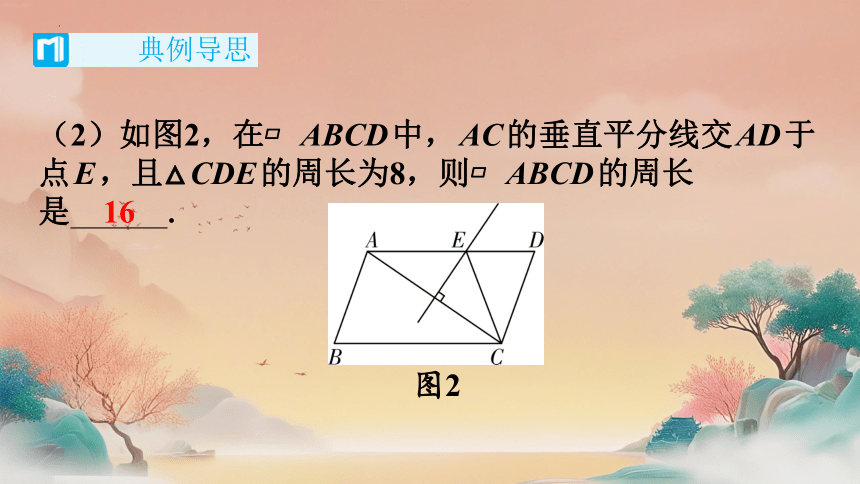
(2)如图2,在 ABCD中,AC的垂直平分线交AD于
点E,且△CDE的周长为8,则 ABCD的周长
是 .
16
图2
1. 在 ABCD中,若∠A=80°,则∠B的度数
是 .
100°
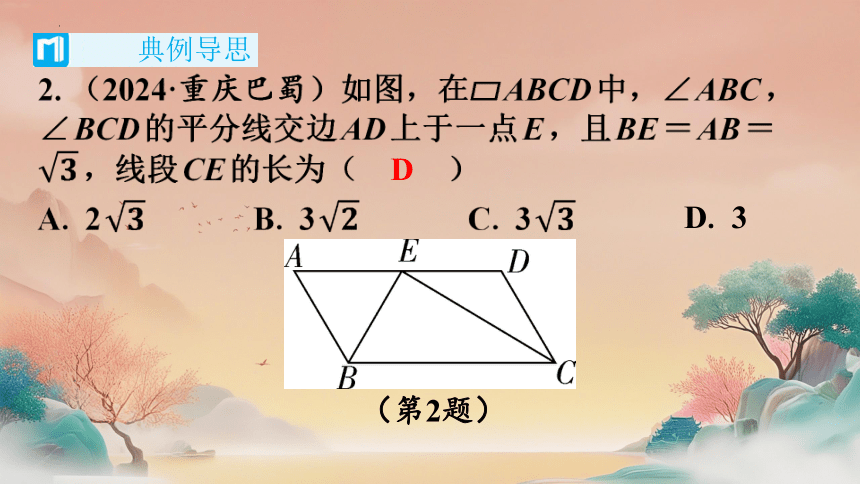
2. (2024·重庆巴蜀)如图,在 ABCD中,∠ABC,
∠BCD的平分线交边AD上于一点E,且BE=AB=
,线段CE的长为( D )
D. 3
(第2题)
D
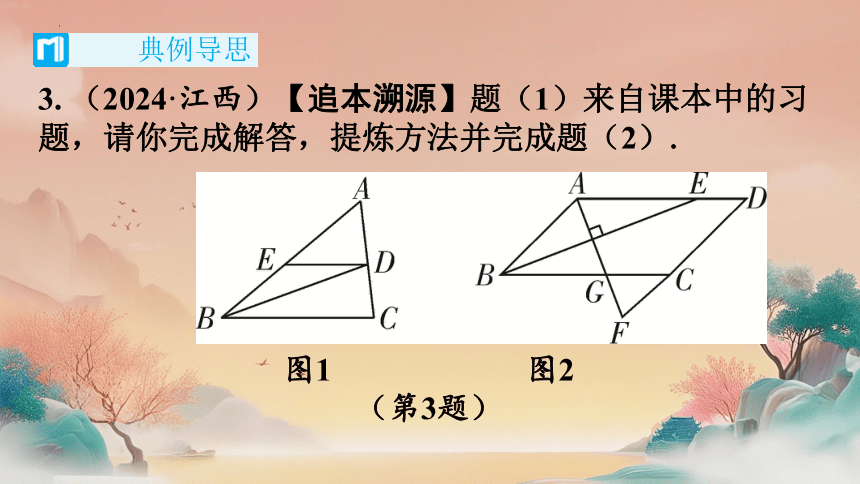
3. (2024·江西)【追本溯源】题(1)来自课本中的习
题,请你完成解答,提炼方法并完成题(2).
图1 图2
(第3题)
(1)如图1,在△ABC中,BD平分∠ABC,交AC于
点D,过点D作BC的平行线,交AB于点E,请判断
△BDE的形状,并说明理由;
解:(1)△BDE是等腰三角形,理由如下:
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵DE∥BC,∴∠BDE=∠CBD,
∴∠BDE=∠ABD,
∴EB=ED,∴△BDE是等腰三角形.
图1
(2)如图2,在 ABCD中,BE平分∠ABC,交边AD
于点E,过点A作AF⊥BE交DC的延长线于点F,交
BC于点G.
①图中一定是等腰三角形的有( B )
A. 3个 B. 4个
C. 5个 D. 6个
B
【方法应用】
图2
②已知AB=3,BC=5,求CF的长.
(2)①由题易知,△ABE,△ABG,
△ADF,△CGF是等腰三角形.故选B.
图2
②∵在 ABCD中,AB=3,BC=5,
∴AB=CD=3,BC=AD=5.
∵BE平分∠ABC,
AD∥BC,
∴∠ABE=∠CBE=∠AEB,
∴△ABE是等腰三角形.
∵AF⊥BE,∴∠BAF=∠EAF
∵AB∥CD,∴∠BAF=∠DFA,
∴∠EAF=∠DFA,
∴AD=DF.
∴CF=DF-CD=AD-CD=5-3=2.
题型二两平行线间的距离
如图,四边形ABCD是平行四边形.
(1)请在图中画出可以表示AB与CD之间,AD与CB
之间的距离的线段;
解:(1)如答案图,过点D作DE⊥AB于点E,
DF⊥BC于点F,则DE,DF分别表示AB与CD之
间,AD与CB之间的距离.(答案不唯一)
(答案图)
(2)若AB=6,CB=3,AD与CB之间的距离是4,
求AB与CD之间的距离.
(2)由题意可知,AB·DE=CB·DF.
∵AB=6,CB=3,DF=4,
∴6DE=3×4,解得DE=2.
∴AB与CD之间的距离为2.
4. (2024·重庆育才)如图,在 ABCD中,AE⊥BC
于点E,AF⊥CD于点F,AE=3,AF=7, ABCD
的周长为60,则 ABCD的面积是( C )
A. 36 B. 48
C. 63 D. 75
(第4题)
C
5. 如图,直线AE∥BD,点C在BD上.若AE=4,BD
=8,△ABD的面积为16,则△ACE的面积为 .
(第5题)
8
1. 平行四边形的对角线的性质
平行四边形的对角线 .
互相平分
符号语言:
如图,∵四边形ABCD是平行四边形,
∴OA= ,OD= .
OC
OB
2. 平行四边形中全等及面积相等的三角形
ABCD中,AC与BD交于点O,则
△ADC≌ ,△ADB≌ ,
△ADO≌ ,△AOB≌ ,
且△ADC,△CBA,△ADB,△CBD的面积相等,等
于 ABCD面积的 ;△ADO,△CBO,△AOB,
△COD的面积相等,等于 ABCD面积的 .
△CBA
△CBD
△CBO
△COD
3. 基本图形及结论
如图,AC,BD交于点O,直线EF过点O,分别交平
行四边形各边所在直线于点E,F.
结论:①OE=OF;
②平行四边形ABCD被直线EF所分的两个四边形面积
相等.(即过平行四边形对角线交点的任意一条直线将
平行四边形的面积平分)
题型一平行四边形对角线的性质的应用
如图, ABCD的对角线AC,BD相交于点O,
△ABO的周长为23 cm,AD比CD长2 cm,AC+BD=
34 cm,求 ABCD的周长.
[分析] 由平行四边形的对边相等、对角线互相平分的性
质可知AB=CD,AD=BC,OC=OA,OB=OD,
则AC+BD=2(OA+OB),结合△ABO的周长可求
出 ABCD较短边的长,再求出较长边的长,进而求出
其周长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OD=OB,OA=OC.
∴AC+BD=2(OA+OB)=34 cm.
则OA+OB=17 cm.
∵△ABO的周长为23 cm,
∴CD=AB=23-17=6(cm).
∵AD比CD长2 cm,∴AD=8 cm.
∴ ABCD的周长为(6+8)×2=28(cm).
[思维点拨] 当题目中出现平行四边形的对角线时,常利
用对角线互相平分的性质寻找相等的线段.
1. (2024·重庆南开)如图,在 ABCD中,AC,BD
交于点O,OE⊥AC交AD于点E,连接CE,若△DCE
的周长为14,则 ABCD的周长为( C )
A. 7 B. 14
C. 28 D. 56
C
(第1题)
2. 如图,在 ABCD中,对角线AC与BD相交于点O,
过点O的直线EF与BA,DC的延长线分别交于点E,
F. 求证:AE=CF.
(第2题)
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD. ∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).∴AE=CF.
题型二平行四边形性质的综合应用
如图,在 ABCD中,点O是对角线AC的中点,过点O的直线EF分别交BC,AD于点E,F. 求证:
(1)△AOF≌△COE;
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC. ∴∠FAO=∠ECO,∠AFO=∠CEO.
∵点O是AC的中点,∴AO=CO.
∴△AOF≌△COE(AAS).
(2)BE=DF.
(2)由(1)知△AOF≌△COE,∴AF=CE.
又∵四边形ABCD为平行四边形,
∴BC=AD.
∴BC-CE=AD-AF,
即BE=DF.
[思维点拨] 平行四边形的对角线将平行四边形分成了一
些全等的三角形,利用全等三角形的性质,可以证明线
段相等、角相等.
3. 如图,EF过 ABCD对角线的交点O,交AD于点
E,交BC于点F. 则下列说法:
(第3题)
①OE=OF;
②图中共有4对全等三角形;
③若AB=4,AC=6,则2<BD<14;
④S四边形ABFE=S△ABC.
其中正确的有( C )
A. ①④ B. ①②④
C
C. ①③④ D. ①②③
4. 如图,在 ABCD中,AB=10,AD=6,
AC⊥BC,则BD= .
(第4题)
4
5. 如图所示, ABCD的对角线AC与BD相交于点O,
AE⊥BC,垂足为E,AB= ,AC=2,BD=4.
(第5题)
(1)求证:AB⊥AC;
(1)证明:∵四边形ABCD为平行四边形,
AC=2,BD=4,
∴OA= AC=1,OB= BD=2.
又∵AB= ,
∴OA2+AB2=OB2,
∴△BAO为直角三角形,且∠BAO=90°,
∴AB⊥AC.
(2)求AE的长.
(2)解:∵△BAC为直角三角形,且∠BAC=90°,
∴BC2=AB2+AC2.
∵AB= ,AC=2,
∴BC= = ,
∴S ABCD=AE·BC=AB·AC,
∴AE= = .
(第5题)
18.1 平行四边形
18.1.1 平行四边形的性质
第1课时 平行四边形的边、角的性质
1. 平行四边形的定义
两组对边 的四边形叫做平行四边形.平行
四边形用符号“ ”表示.
分别平行
(2)已知:如图,在 ABCD中,∠BAD的平分线交
CD于点E,∠ABC的平分线交CD于点F.
结论:①AD=DE,CF=CB,DE=CF;
②AE⊥BF.
(3)已知:如图,在 ABCD中,AE⊥BC,
AF⊥CD,垂足分别为E,F.
结论:①S ABCD=BC·AE=CD·AF;
②∠B=∠EAF=∠D,∠C+∠EAF=180°.
题型一平行四边形的边、角的性质的应用
(1)平行四边形ABCD中,
∠A∶∠B∶∠C∶∠D的值可以是( B )
A. 1∶2∶3∶4 B. 5∶6∶5∶6
C. 2∶4∶4∶5 D. 4∶4∶3∶3
B
(2)如图,在 ABCD中,AE⊥CD,若∠B=
60°,则∠DAE的度数是 °.
30
(1)如图1,在平行四边形ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点F. 若AB=5,BC=3,则EC的长度是( C )
C
A. 1 B. 1.5
C. 2 D. 2.5
图1
(2)如图2,在 ABCD中,AC的垂直平分线交AD于
点E,且△CDE的周长为8,则 ABCD的周长
是 .
16
图2
1. 在 ABCD中,若∠A=80°,则∠B的度数
是 .
100°
2. (2024·重庆巴蜀)如图,在 ABCD中,∠ABC,
∠BCD的平分线交边AD上于一点E,且BE=AB=
,线段CE的长为( D )
D. 3
(第2题)
D
3. (2024·江西)【追本溯源】题(1)来自课本中的习
题,请你完成解答,提炼方法并完成题(2).
图1 图2
(第3题)
(1)如图1,在△ABC中,BD平分∠ABC,交AC于
点D,过点D作BC的平行线,交AB于点E,请判断
△BDE的形状,并说明理由;
解:(1)△BDE是等腰三角形,理由如下:
∵BD平分∠ABC,∴∠ABD=∠CBD.
∵DE∥BC,∴∠BDE=∠CBD,
∴∠BDE=∠ABD,
∴EB=ED,∴△BDE是等腰三角形.
图1
(2)如图2,在 ABCD中,BE平分∠ABC,交边AD
于点E,过点A作AF⊥BE交DC的延长线于点F,交
BC于点G.
①图中一定是等腰三角形的有( B )
A. 3个 B. 4个
C. 5个 D. 6个
B
【方法应用】
图2
②已知AB=3,BC=5,求CF的长.
(2)①由题易知,△ABE,△ABG,
△ADF,△CGF是等腰三角形.故选B.
图2
②∵在 ABCD中,AB=3,BC=5,
∴AB=CD=3,BC=AD=5.
∵BE平分∠ABC,
AD∥BC,
∴∠ABE=∠CBE=∠AEB,
∴△ABE是等腰三角形.
∵AF⊥BE,∴∠BAF=∠EAF
∵AB∥CD,∴∠BAF=∠DFA,
∴∠EAF=∠DFA,
∴AD=DF.
∴CF=DF-CD=AD-CD=5-3=2.
题型二两平行线间的距离
如图,四边形ABCD是平行四边形.
(1)请在图中画出可以表示AB与CD之间,AD与CB
之间的距离的线段;
解:(1)如答案图,过点D作DE⊥AB于点E,
DF⊥BC于点F,则DE,DF分别表示AB与CD之
间,AD与CB之间的距离.(答案不唯一)
(答案图)
(2)若AB=6,CB=3,AD与CB之间的距离是4,
求AB与CD之间的距离.
(2)由题意可知,AB·DE=CB·DF.
∵AB=6,CB=3,DF=4,
∴6DE=3×4,解得DE=2.
∴AB与CD之间的距离为2.
4. (2024·重庆育才)如图,在 ABCD中,AE⊥BC
于点E,AF⊥CD于点F,AE=3,AF=7, ABCD
的周长为60,则 ABCD的面积是( C )
A. 36 B. 48
C. 63 D. 75
(第4题)
C
5. 如图,直线AE∥BD,点C在BD上.若AE=4,BD
=8,△ABD的面积为16,则△ACE的面积为 .
(第5题)
8
1. 平行四边形的对角线的性质
平行四边形的对角线 .
互相平分
符号语言:
如图,∵四边形ABCD是平行四边形,
∴OA= ,OD= .
OC
OB
2. 平行四边形中全等及面积相等的三角形
ABCD中,AC与BD交于点O,则
△ADC≌ ,△ADB≌ ,
△ADO≌ ,△AOB≌ ,
且△ADC,△CBA,△ADB,△CBD的面积相等,等
于 ABCD面积的 ;△ADO,△CBO,△AOB,
△COD的面积相等,等于 ABCD面积的 .
△CBA
△CBD
△CBO
△COD
3. 基本图形及结论
如图,AC,BD交于点O,直线EF过点O,分别交平
行四边形各边所在直线于点E,F.
结论:①OE=OF;
②平行四边形ABCD被直线EF所分的两个四边形面积
相等.(即过平行四边形对角线交点的任意一条直线将
平行四边形的面积平分)
题型一平行四边形对角线的性质的应用
如图, ABCD的对角线AC,BD相交于点O,
△ABO的周长为23 cm,AD比CD长2 cm,AC+BD=
34 cm,求 ABCD的周长.
[分析] 由平行四边形的对边相等、对角线互相平分的性
质可知AB=CD,AD=BC,OC=OA,OB=OD,
则AC+BD=2(OA+OB),结合△ABO的周长可求
出 ABCD较短边的长,再求出较长边的长,进而求出
其周长.
解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OD=OB,OA=OC.
∴AC+BD=2(OA+OB)=34 cm.
则OA+OB=17 cm.
∵△ABO的周长为23 cm,
∴CD=AB=23-17=6(cm).
∵AD比CD长2 cm,∴AD=8 cm.
∴ ABCD的周长为(6+8)×2=28(cm).
[思维点拨] 当题目中出现平行四边形的对角线时,常利
用对角线互相平分的性质寻找相等的线段.
1. (2024·重庆南开)如图,在 ABCD中,AC,BD
交于点O,OE⊥AC交AD于点E,连接CE,若△DCE
的周长为14,则 ABCD的周长为( C )
A. 7 B. 14
C. 28 D. 56
C
(第1题)
2. 如图,在 ABCD中,对角线AC与BD相交于点O,
过点O的直线EF与BA,DC的延长线分别交于点E,
F. 求证:AE=CF.
(第2题)
证明:∵四边形ABCD是平行四边形,
∴OA=OC,AB∥CD. ∴∠AEO=∠CFO.
在△AOE和△COF中,
∴△AOE≌△COF(AAS).∴AE=CF.
题型二平行四边形性质的综合应用
如图,在 ABCD中,点O是对角线AC的中点,过点O的直线EF分别交BC,AD于点E,F. 求证:
(1)△AOF≌△COE;
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC. ∴∠FAO=∠ECO,∠AFO=∠CEO.
∵点O是AC的中点,∴AO=CO.
∴△AOF≌△COE(AAS).
(2)BE=DF.
(2)由(1)知△AOF≌△COE,∴AF=CE.
又∵四边形ABCD为平行四边形,
∴BC=AD.
∴BC-CE=AD-AF,
即BE=DF.
[思维点拨] 平行四边形的对角线将平行四边形分成了一
些全等的三角形,利用全等三角形的性质,可以证明线
段相等、角相等.
3. 如图,EF过 ABCD对角线的交点O,交AD于点
E,交BC于点F. 则下列说法:
(第3题)
①OE=OF;
②图中共有4对全等三角形;
③若AB=4,AC=6,则2<BD<14;
④S四边形ABFE=S△ABC.
其中正确的有( C )
A. ①④ B. ①②④
C
C. ①③④ D. ①②③
4. 如图,在 ABCD中,AB=10,AD=6,
AC⊥BC,则BD= .
(第4题)
4
5. 如图所示, ABCD的对角线AC与BD相交于点O,
AE⊥BC,垂足为E,AB= ,AC=2,BD=4.
(第5题)
(1)求证:AB⊥AC;
(1)证明:∵四边形ABCD为平行四边形,
AC=2,BD=4,
∴OA= AC=1,OB= BD=2.
又∵AB= ,
∴OA2+AB2=OB2,
∴△BAO为直角三角形,且∠BAO=90°,
∴AB⊥AC.
(2)求AE的长.
(2)解:∵△BAC为直角三角形,且∠BAC=90°,
∴BC2=AB2+AC2.
∵AB= ,AC=2,
∴BC= = ,
∴S ABCD=AE·BC=AB·AC,
∴AE= = .
(第5题)
