19.1.2 函数的图象(课时1) 课件(共55张PPT)2024-2025学年 人教版数学八年级下册
文档属性
| 名称 | 19.1.2 函数的图象(课时1) 课件(共55张PPT)2024-2025学年 人教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览





文档简介
(共55张PPT)
19.1.2函数的图象
(课时1)
第十九章 一次函数
探究新知
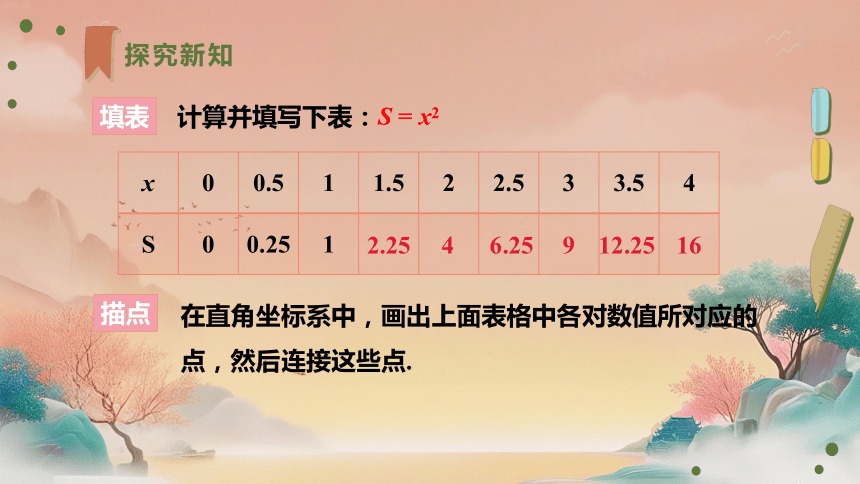
计算并填写下表:
S = x2
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
2.25
4
6.25
9
12.25
16
在直角坐标系中,画出上面表格中各对数值所对应的点,然后连接这些点.
填表
描点
归纳总结
函数S=x2(x>0)的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
通过图象可以数形结合地研究函数.
归纳总结
描点法画函数图象的一般步骤如下:
第一步:列表——表中给出一些自变量的值及其对应的函数值;
第二步:描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线——按照横坐标由小到大的顺序,把所描出的各点用光滑曲线连接起来.
例题练习
在下列式子中,对于 x 的每一个确定的值,y 有唯一的对应值,即y 是 x 的函数.画出这些函数的图象:
(1) y=x+0.5;
(2)
解:(1)从式子 y = x+0.5可以看出,x 取任意实数时这个式子都有意义,所以 x 的取值范围是全体实数.
从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写下表中空格) .
x … 3 2 1 0 1 2 3 …
y … 0.5 0.5 1.5 2.5 …
2.5
1.5
3.5
例题练习
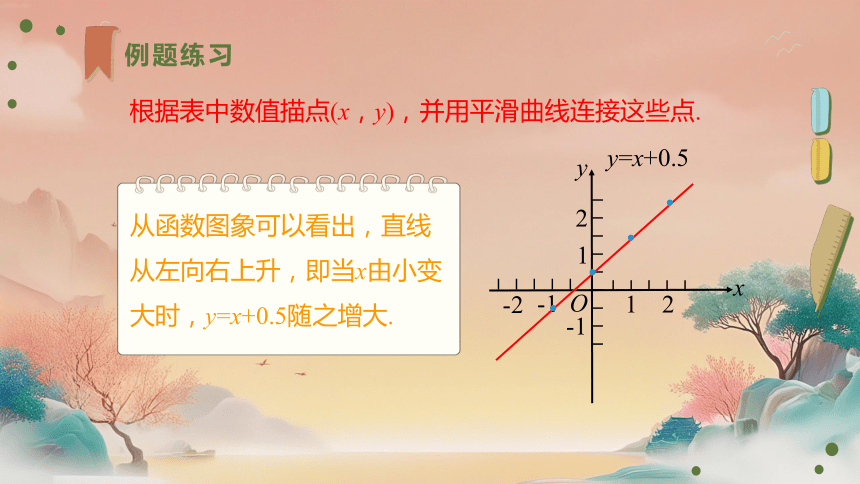
根据表中数值描点(x,y),并用平滑曲线连接这些点.
从函数图象可以看出,直线从左向右上升,即当x由小变大时,y=x+0.5随之增大.
O
1
2
1
-1
2
-2
-1
x
y
y=x+0.5
例题练习
解:(2)
列表(计算并填写下表中空格)
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.714
1.2
1
例题练习
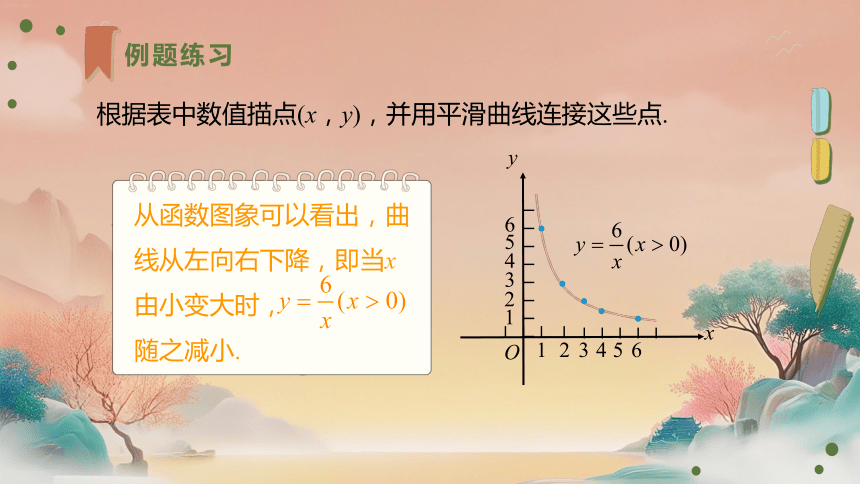
根据表中数值描点(x,y),并用平滑曲线连接这些点.
O
1
2
1
3
2
3
4
x
y
5
6
4
5
6
从函数图象可以看出,曲线从左向右下降,即当x由小变大时, 随之减小.
探究新知
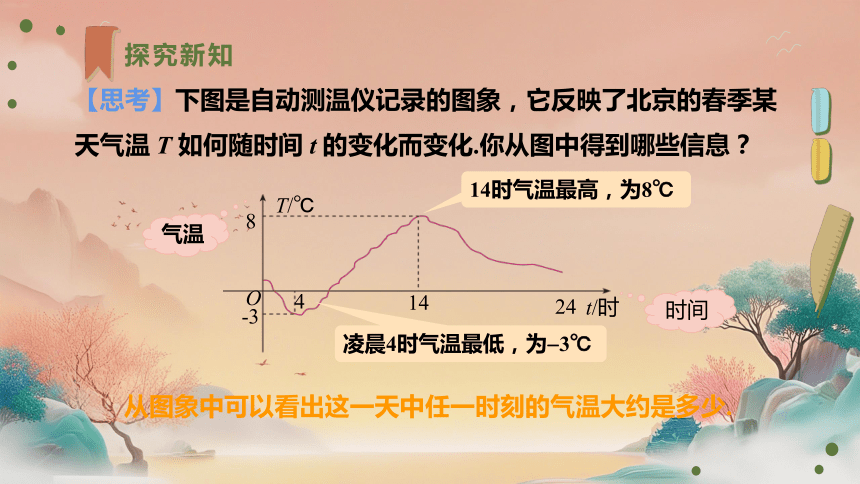
【思考】下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.你从图中得到哪些信息?
-3
O
4
14
24
8
T/℃
t/时
从图象中可以看出这一天中任一时刻的气温大约是多少.
时间
气温
凌晨4时气温最低,为 3℃
14时气温最高,为8℃
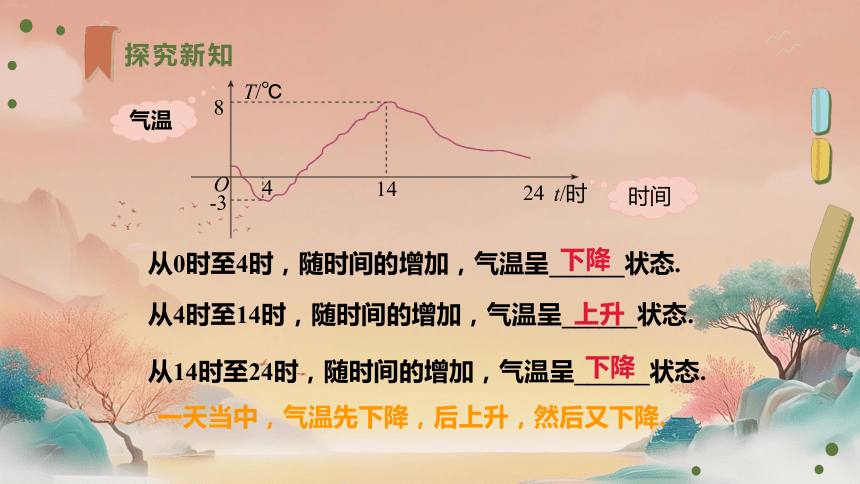
探究新知
从4时至14时,随时间的增加,气温呈______状态.
从14时至24时,随时间的增加,气温呈______状态.
上升
下降
一天当中,气温先下降,后上升,然后又下降.
-3
O
4
14
24
8
T/℃
t/时
时间
气温
从0时至4时,随时间的增加,气温呈______状态.
下降
探究新知
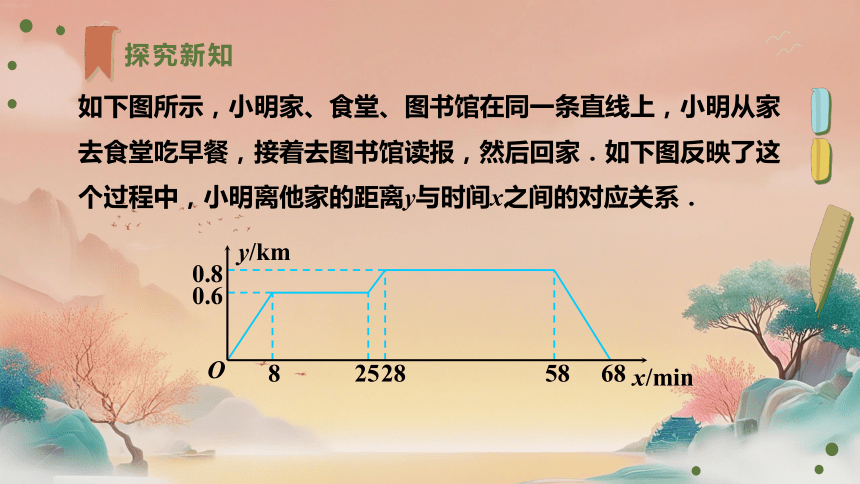
如下图所示,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如下图反映了这个过程中,小明离他家的距离y与时间x之间的对应关系.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
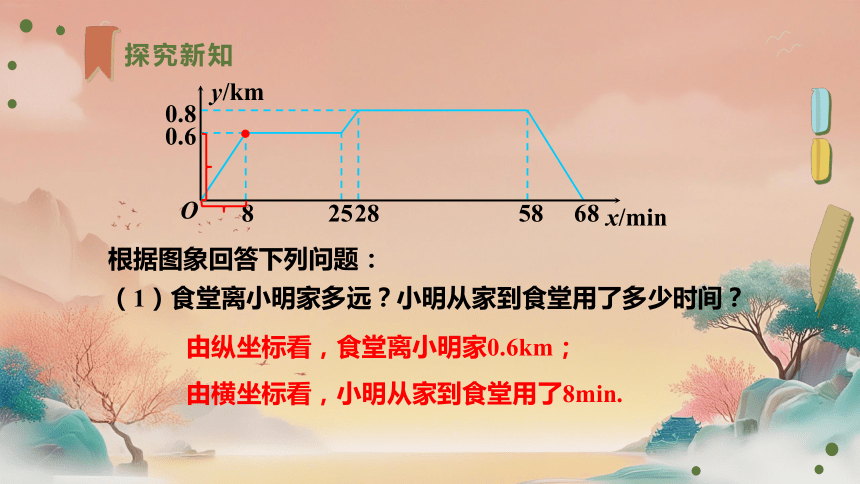
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
由纵坐标看,食堂离小明家0.6km;
由横坐标看,小明从家到食堂用了8min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(2)小明在食堂吃早餐用了多少时间?
在食堂
吃早餐
由横坐标看,25-8=17,小明吃早餐用了17min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
由纵坐标看,0.8-0.6=0.2,食堂离图书馆0.2km.
由横坐标看,28-25=3,小明从食堂到图书馆用了3min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多长时间?
在图书馆读报
由横坐标看,58-28=30,小明读报用了30min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
平均速度=路程÷行走时间
由纵坐标可得,图书馆离小明家0.8km.
由横坐标看,68-58=10;小明从图书馆回家用了10min,
0.8÷10=0.08,小明回家的平均速度为0.08km/min.
归纳总结
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
步骤:(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
D
B
练习3 2025年央视春晚在重庆设立分会场,场地在来福士对面的规划展览馆,很多明星将参与春晚彩排,家住长嘉汇购物公园旁的小西,在寒假某一天,先从家跑步去规划展览馆拍照打卡,再去面馆打包“重庆小面”,最后回家.小西家、面馆、规划展览馆在一条直线上.小西离开家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
D
练习4 已知小明家、图书馆和学校在一条直线上,某天小明从家骑自行车去上学,先到图书馆挑选了一些学习资料后,再骑车去学校.若小明离家的距离用y表示,出发时间用x表示,y与x之间的关系如图所示,则下列结论正确的是( )
D
A.小明在图书馆停留了10分钟
B.小明家距离学校1000米
C.小明从图书馆到学校用了25分钟
D.从图书馆到学校的速度是110米/分钟
练习5 周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
C
A.小丽从家到达公园共用时间20分钟.
B.公园离小丽家的距离为2000米.
C.小丽在便利店时间为15分钟.
D.便利店离小丽家的距离为1000米.
探究新知
解析式法:用数学式子表示函数关系的方法叫做解析式法,其中的等式叫做函数解析式.
如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)请你写出y与x之间的函数解析式吗?
解:
长方形的周长 = 2(长+宽)
∴y与x之间的函数解析式为
y = 2 ( x + )
( x 0 )
x
探究新知
解析式法有什么优缺点呢?
能准确地反映整个变化过程中自变量与函数的对应关系.
优点
缺点
很难直观地看出函数的变化规律,而且有些函数不能用解析式法表示出来,如气温与时间的函数关系.
探究新知
列表法:通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫做列表法.
(2)当 x 的值分别为1,2,3,4,5时,请列表表示变量之间的对应关系.
y = 2 ( x + )
( x 0 )
x/m 1 2 3 4 5
y/m 26 16 14 14 14.8
探究新知
列表法有什么优缺点呢?
一目了然,对表格中已有自变量的每一个值,可直接找到与它对应的函数值.
优点
缺点
列出的对应值是有限的,而且在表格中也不容易看出自变量与函数的变化规律.
探究新知
图象法:用图象表示两个变量间的函数关系的方法叫做图象法.
x/m 1 2 3 4 5
y/m 26 16 14 14 14.8
(3)能画出函数的图象吗?
40
35
30
25
20
15
10
5
O
5
10
y = 2 ( x + )
( x 0 )
探究新知
图象法有什么优缺点呢?
直观、形象地反映出函数关系变化的趋势和某些性质.
优点
缺点
从自变量的值常常难以找到对应函数的准确值.
归纳总结
请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表:
表示方法 全面性 准确性 直观性 形象性
列表法
解析式法
图象法
从所填表格中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
√
×
×
×
×
×
√
√
√
√
√
×
探究新知
一个水库的水位在最近5h内持续上涨,下表记录了这5h内 6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你能发现水位变化有什么规律吗?
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
可以看出,这6个点在同一直线上,且每小时水位上升 0.3 m.
由此猜想,如果画出这 5 h 内其他时刻(如 t=2.5 h 等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度均匀上升的.
探究新知
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象. 这个函数能表示水位的变化规律吗?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
由于水位在最近 5h 内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以 y 是 t 的函数.
探究新知
+0.3
+0.3
+0.3
+0.3
+0.3
故函数解析式为 y=0.3t+3(0≤t≤5)
它表示经过t h水位上升0.3t m,即水位y为(0.3t+3) m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
其函数的图象是图中点 A(0,3)和点B(5,4.5)之间的线段 AB .
A
B
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
A
B
y=0.3t+3(0≤t≤5)
1.如果在这5h内,水位一直匀速上升,即升速0.3m/h,那么函数y=0.3t+3(0≤t ≤5)就精确地表示了这种变化规律.
2. 即使在这5h内,水位的升速有些变化,而由于每小时水位上升0.3m是确定的,因此这个函数也可以近似地表示水位的变化规律.
探究新知
(3)据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米?
如果水位的变化规律不变,则可利用函数 y=0.3t+3 进行预测.
再过2h,即t=5+2=7(h)时,
水位高度为:y=0.3×7+3=5.1(m)
探究新知
把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,从图象也能看出这时的水位高度约为 5.1 m.
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
A
B
y=0.3t+3(0≤t≤5)
5.1
B
(1)上表反映了哪两个变量之间的关系
解:(1)∵游泳池的存水随放水时间变化而改变
∴在这个变化过程中,自变量是放水时间,因变量是游泳池的存水.
(2)请将上述表格补充完整、
(3)设放水时间为t小时,游泳池的存水量为Q立方米,写出Q与t之间的关系式.(不要求写自变量范围)
放水时间小时 1 2 3 4 5 6 7
游泳池的存水/立方米 858 780 702 546
624
468
390
B
A
B
35
小结
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
谢谢同学们的聆听
19.1.2函数的图象
(课时1)
第十九章 一次函数
探究新知
计算并填写下表:
S = x2
x 0 0.5 1 1.5 2 2.5 3 3.5 4
S 0 0.25 1
2.25
4
6.25
9
12.25
16
在直角坐标系中,画出上面表格中各对数值所对应的点,然后连接这些点.
填表
描点
归纳总结
函数S=x2(x>0)的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
通过图象可以数形结合地研究函数.
归纳总结
描点法画函数图象的一般步骤如下:
第一步:列表——表中给出一些自变量的值及其对应的函数值;
第二步:描点——在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
第三步:连线——按照横坐标由小到大的顺序,把所描出的各点用光滑曲线连接起来.
例题练习
在下列式子中,对于 x 的每一个确定的值,y 有唯一的对应值,即y 是 x 的函数.画出这些函数的图象:
(1) y=x+0.5;
(2)
解:(1)从式子 y = x+0.5可以看出,x 取任意实数时这个式子都有意义,所以 x 的取值范围是全体实数.
从x的取值范围中选取一些数值,算出y的对应值,列表(计算并填写下表中空格) .
x … 3 2 1 0 1 2 3 …
y … 0.5 0.5 1.5 2.5 …
2.5
1.5
3.5
例题练习
根据表中数值描点(x,y),并用平滑曲线连接这些点.
从函数图象可以看出,直线从左向右上升,即当x由小变大时,y=x+0.5随之增大.
O
1
2
1
-1
2
-2
-1
x
y
y=x+0.5
例题练习
解:(2)
列表(计算并填写下表中空格)
x … 0.5 1 1.5 2 2.5 3 3.5 4 5 6 …
y … 6 3 2 1.5 …
12
4
2.4
1.714
1.2
1
例题练习
根据表中数值描点(x,y),并用平滑曲线连接这些点.
O
1
2
1
3
2
3
4
x
y
5
6
4
5
6
从函数图象可以看出,曲线从左向右下降,即当x由小变大时, 随之减小.
探究新知
【思考】下图是自动测温仪记录的图象,它反映了北京的春季某天气温 T 如何随时间 t 的变化而变化.你从图中得到哪些信息?
-3
O
4
14
24
8
T/℃
t/时
从图象中可以看出这一天中任一时刻的气温大约是多少.
时间
气温
凌晨4时气温最低,为 3℃
14时气温最高,为8℃
探究新知
从4时至14时,随时间的增加,气温呈______状态.
从14时至24时,随时间的增加,气温呈______状态.
上升
下降
一天当中,气温先下降,后上升,然后又下降.
-3
O
4
14
24
8
T/℃
t/时
时间
气温
从0时至4时,随时间的增加,气温呈______状态.
下降
探究新知
如下图所示,小明家、食堂、图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如下图反映了这个过程中,小明离他家的距离y与时间x之间的对应关系.
8
25
28
58
68
x/min
0.8
0.6
y/km
O
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
由纵坐标看,食堂离小明家0.6km;
由横坐标看,小明从家到食堂用了8min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(2)小明在食堂吃早餐用了多少时间?
在食堂
吃早餐
由横坐标看,25-8=17,小明吃早餐用了17min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
由纵坐标看,0.8-0.6=0.2,食堂离图书馆0.2km.
由横坐标看,28-25=3,小明从食堂到图书馆用了3min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(4)小明读报用了多长时间?
在图书馆读报
由横坐标看,58-28=30,小明读报用了30min.
探究新知
8
25
28
58
68
x/min
0.8
0.6
y/km
O
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
平均速度=路程÷行走时间
由纵坐标可得,图书馆离小明家0.8km.
由横坐标看,68-58=10;小明从图书馆回家用了10min,
0.8÷10=0.08,小明回家的平均速度为0.08km/min.
归纳总结
解答图象信息题主要运用数形结合思想,化图象信息为数字信息.
步骤:(1)了解横、纵轴的意义;
(2)从 上判定函数与自变量的关系;
(3)抓住图象中端点,拐点等特殊点的实际意义.
图象形状
D
B
练习3 2025年央视春晚在重庆设立分会场,场地在来福士对面的规划展览馆,很多明星将参与春晚彩排,家住长嘉汇购物公园旁的小西,在寒假某一天,先从家跑步去规划展览馆拍照打卡,再去面馆打包“重庆小面”,最后回家.小西家、面馆、规划展览馆在一条直线上.小西离开家的距离y与时间x之间的函数关系如图所示.下列结论正确的是( )
D
练习4 已知小明家、图书馆和学校在一条直线上,某天小明从家骑自行车去上学,先到图书馆挑选了一些学习资料后,再骑车去学校.若小明离家的距离用y表示,出发时间用x表示,y与x之间的关系如图所示,则下列结论正确的是( )
D
A.小明在图书馆停留了10分钟
B.小明家距离学校1000米
C.小明从图书馆到学校用了25分钟
D.从图书馆到学校的速度是110米/分钟
练习5 周末小丽从家里出发骑单车去公园,因为她家与公园之间是一条笔直的自行车道,所以小丽骑得特别放松.途中,她在路边的便利店挑选一瓶矿泉水,耽误了一段时间后继续骑行,愉快地到了公园.图中描述了小丽路上的情景,下列说法中错误的是( )
C
A.小丽从家到达公园共用时间20分钟.
B.公园离小丽家的距离为2000米.
C.小丽在便利店时间为15分钟.
D.便利店离小丽家的距离为1000米.
探究新知
解析式法:用数学式子表示函数关系的方法叫做解析式法,其中的等式叫做函数解析式.
如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)请你写出y与x之间的函数解析式吗?
解:
长方形的周长 = 2(长+宽)
∴y与x之间的函数解析式为
y = 2 ( x + )
( x 0 )
x
探究新知
解析式法有什么优缺点呢?
能准确地反映整个变化过程中自变量与函数的对应关系.
优点
缺点
很难直观地看出函数的变化规律,而且有些函数不能用解析式法表示出来,如气温与时间的函数关系.
探究新知
列表法:通过列出自变量的值与对应函数值的表格来表示函数关系的方法叫做列表法.
(2)当 x 的值分别为1,2,3,4,5时,请列表表示变量之间的对应关系.
y = 2 ( x + )
( x 0 )
x/m 1 2 3 4 5
y/m 26 16 14 14 14.8
探究新知
列表法有什么优缺点呢?
一目了然,对表格中已有自变量的每一个值,可直接找到与它对应的函数值.
优点
缺点
列出的对应值是有限的,而且在表格中也不容易看出自变量与函数的变化规律.
探究新知
图象法:用图象表示两个变量间的函数关系的方法叫做图象法.
x/m 1 2 3 4 5
y/m 26 16 14 14 14.8
(3)能画出函数的图象吗?
40
35
30
25
20
15
10
5
O
5
10
y = 2 ( x + )
( x 0 )
探究新知
图象法有什么优缺点呢?
直观、形象地反映出函数关系变化的趋势和某些性质.
优点
缺点
从自变量的值常常难以找到对应函数的准确值.
归纳总结
请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表:
表示方法 全面性 准确性 直观性 形象性
列表法
解析式法
图象法
从所填表格中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
√
×
×
×
×
×
√
√
√
√
√
×
探究新知
一个水库的水位在最近5h内持续上涨,下表记录了这5h内 6个时间点的水位高度,其中 t 表示时间,y 表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你能发现水位变化有什么规律吗?
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
可以看出,这6个点在同一直线上,且每小时水位上升 0.3 m.
由此猜想,如果画出这 5 h 内其他时刻(如 t=2.5 h 等)及其水位高度所对应的点,它们可能也在这条直线上,即在这个时间段中水位可能是始终以同一速度均匀上升的.
探究新知
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象. 这个函数能表示水位的变化规律吗?
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
由于水位在最近 5h 内持续上涨,对于时间 t 的每一个确定的值,水位高度 y 都有唯一的值与其对应,所以 y 是 t 的函数.
探究新知
+0.3
+0.3
+0.3
+0.3
+0.3
故函数解析式为 y=0.3t+3(0≤t≤5)
它表示经过t h水位上升0.3t m,即水位y为(0.3t+3) m.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
其函数的图象是图中点 A(0,3)和点B(5,4.5)之间的线段 AB .
A
B
探究新知
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
A
B
y=0.3t+3(0≤t≤5)
1.如果在这5h内,水位一直匀速上升,即升速0.3m/h,那么函数y=0.3t+3(0≤t ≤5)就精确地表示了这种变化规律.
2. 即使在这5h内,水位的升速有些变化,而由于每小时水位上升0.3m是确定的,因此这个函数也可以近似地表示水位的变化规律.
探究新知
(3)据估计这种上涨规律还会持续 2 h,预测再过 2 h 水位高度将达到多少米?
如果水位的变化规律不变,则可利用函数 y=0.3t+3 进行预测.
再过2h,即t=5+2=7(h)时,
水位高度为:y=0.3×7+3=5.1(m)
探究新知
把图中的函数图象(线段AB)向右延伸到 t=7 所对应的位置,从图象也能看出这时的水位高度约为 5.1 m.
x/h
y/m
O
1
2
3
4
5
6
7
1
2
3
4
5
A
B
y=0.3t+3(0≤t≤5)
5.1
B
(1)上表反映了哪两个变量之间的关系
解:(1)∵游泳池的存水随放水时间变化而改变
∴在这个变化过程中,自变量是放水时间,因变量是游泳池的存水.
(2)请将上述表格补充完整、
(3)设放水时间为t小时,游泳池的存水量为Q立方米,写出Q与t之间的关系式.(不要求写自变量范围)
放水时间小时 1 2 3 4 5 6 7
游泳池的存水/立方米 858 780 702 546
624
468
390
B
A
B
35
小结
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
谢谢同学们的聆听
