2025年春甘肃省武威第二十中学八年级数学下册人教版期中模拟试卷(含答案)
文档属性
| 名称 | 2025年春甘肃省武威第二十中学八年级数学下册人教版期中模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 846.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 22:18:49 | ||
图片预览



文档简介
2025春甘肃省武威第二十中学八年级数学下册人教版期中模拟试卷
一、单选题(共30分)
1.(本题3分)下列各式中,从左向右变形正确的是( )
A. B.
C. D.
2.(本题3分)如图,已知△ABC中,AB=,AC=3,BC=1,AB的垂直平分线分别交AC,AB于点D,E,连接BD,则CD的长为( )
A. B. C.1 D.
3.(本题3分)如图,矩形的对角线相交于点,过点作,交于点,连接,若,则的度数是( )
A. B. C. D.
4.(本题3分)若k,m,n都是整数,且=k,=15,=6,则下列关于k,m,n的大小关系,正确的是( )
A.m<k<n B.m=n>k C.m<n<k D.k<m=n
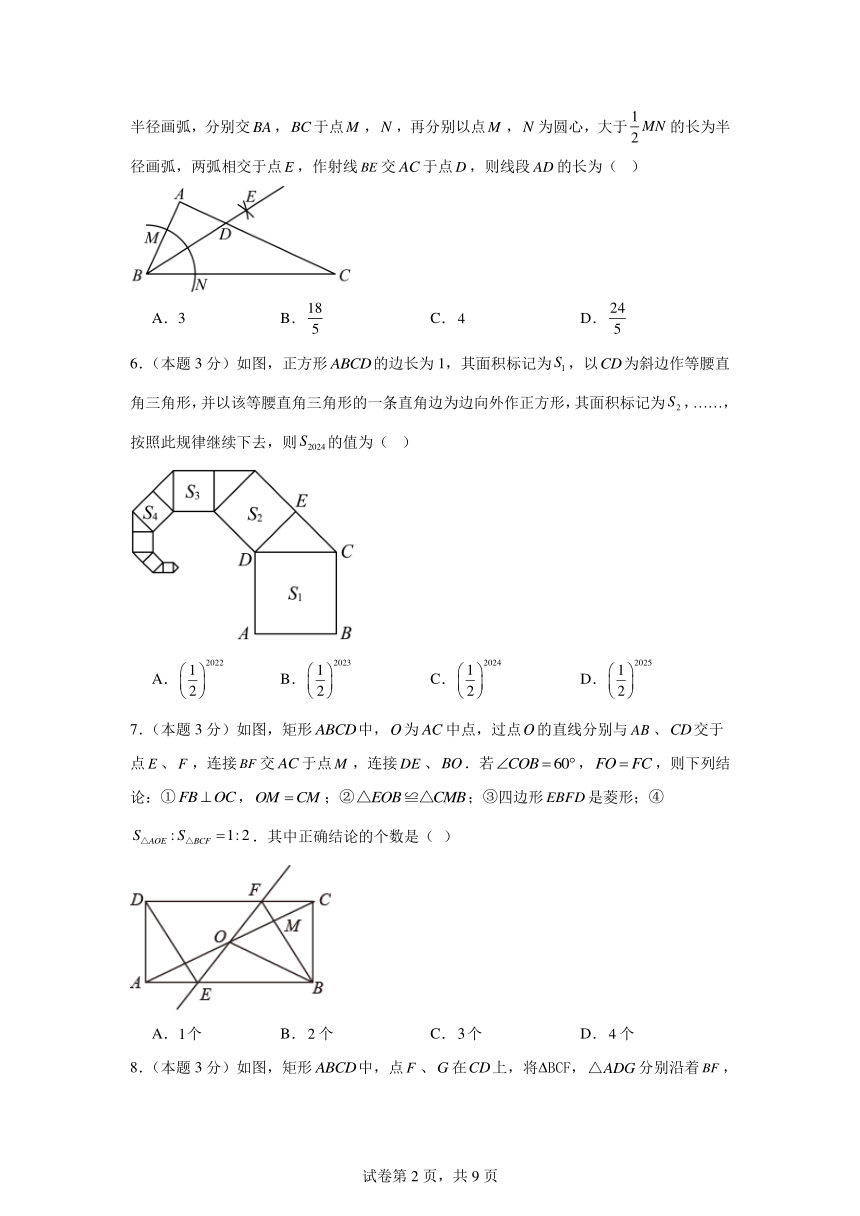
5.(本题3分)如图,在 ABC中,,,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧相交于点,作射线交于点,则线段的长为( )
A.3 B. C. D.
6.(本题3分)如图,正方形的边长为1,其面积标记为,以为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,……,按照此规律继续下去,则的值为( )
A. B. C. D.
7.(本题3分)如图,矩形中,为中点,过点的直线分别与、交于点、,连接交于点,连接、.若,,则下列结论:①,;②;③四边形是菱形;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
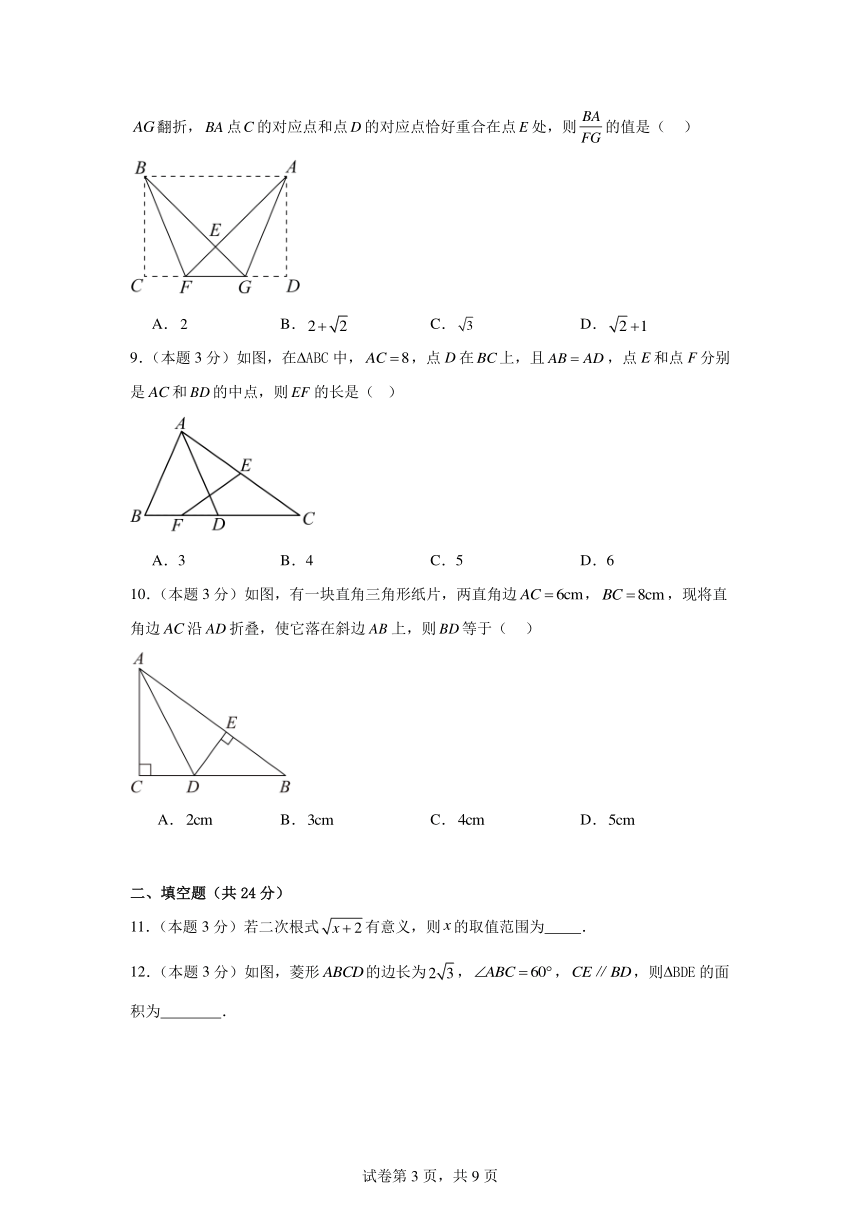
8.(本题3分)如图,矩形中,点、在上,将 BCF,分别沿着,翻折,点的对应点和点的对应点恰好重合在点处,则的值是( )
A. B. C. D.
9.(本题3分)如图,在 ABC中,,点D在上,且,点E和点F分别是和的中点,则的长是( )
A.3 B.4 C.5 D.6
10.(本题3分)如图,有一块直角三角形纸片,两直角边,,现将直角边沿折叠,使它落在斜边上,则等于( )
A. B. C. D.
二、填空题(共24分)
11.(本题3分)若二次根式有意义,则的取值范围为 .
12.(本题3分)如图,菱形的边长为,,,则 BDE的面积为 .
13.(本题3分)如图,中,,,,点P为上一个动点,以为轴折叠得到,点A的对应点为点Q,当点Q落在内部上时,的取值范围为 .
14.(本题3分)如图,在平行四边形中,点是中点,连接并延长交的延长线于点. 若,,的度数= .
15.(本题3分)如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,大正方形的面积为41,小正方形的面积为1,设直角三角形较短直角边长为a,较长直角边长为b,则的值为 .
16.(本题3分)E,F分别是正方形边,上的点,.以,为边作,连结并延长交于点H,连结.若,则的长为 .
17.(本题3分)如图,把长方形沿直线向上折叠,使点C落在的位置上,已知,,则 .
18.(本题3分)小明将4个全等的直角三角形拼成如图所示的五边形,添加适当的辅助线后,用等面积法建立等式证明勾股定理.小明在证题中用两种方法表示五边形的面积,分别是S1= ,S2= .
三、解答题(共66分)
19.(本题8分)计算.
(1)
(2)
20.(本题6分)已知都是实数,且,求的值.
21.(本题6分)已知:,,满足.
(1)求,,的值;
(2)请判断以,,为边构成的 ABC的形状,并说明理由.
22.(本题6分)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东方向开往B岛,其速度仍为20海里/小时.
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?(结果保留一位小数)
23.(本题8分)如图,在中,,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当,时,求阴影部分的面积.
24.(本题8分)现有两块同样大小的长方形纸片,小星采用如图①所示的方式,在长方形纸片上裁出两块面积分别为和的正方形纸片A,B.
(1)原长方形纸片的周长是_____ (结果化为最简二次根式);
(2)写出图①中阴影部分的长和宽,并求出它的面积;
(3)小红想采用如图②所示的方式,在长方形纸片上裁出面积为的两块正方形纸片,请你判断能否裁出,并说明理由.
25.(本题8分)每年的11月9日是我国的消防日,为了增强全民的消防安全意识,某校师生在消防日举行了消防演练.如图,云梯长为10米,云梯顶端靠在教学楼外墙上(墙与地面垂直),云梯底端与墙角的距离为6米.(结果保留1位小数,参考数据:,,)
(1)求云梯顶端与墙角的距离的长;
(2)假如云梯顶端下方3米处发生火灾,需将云梯顶端下滑到着火点处,则云梯底端在水平方向上滑动的距离为多少米.
26.(本题8分)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
∵,即,
∴的整数部分为2,小数部分为.请解答:
(1)的整数部分是 ,小数部分是 .
(2)已知:,其中x是整数,且,求的相反数.
27.(本题8分)如图①,在矩形纸片中,,.
【实践操作】
第一步:如图②,将图①中的矩形纸片沿过点A的直线折叠,使点D落在上的点E处,折痕为,然后把纸片展平;
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为,然后展平,隐去;
第三步:如图④,将图③中的矩形纸片沿折叠,得到,延长与交于点N,与交于点M.
【问题解决】
(1)在图②中证明四边形是正方形;
(2)请在图④中判断与的数量关系,并加以证明;
(3)请在图④中求的长度.
试卷第1页,共3页
试卷第1页,共3页
《2025春甘肃省武威第二十中学八年级数学下册人教版期中模拟试卷》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A D B C D B D
11.
12.
13.
14.
15.9
16.
17.
18.
19.(1)解:
;
(2)解:
.
20.解:∵,
∴得
∴.
则,
当时,.
21.(1)解:∵,,,
又,
∴,
∴,,
(2)解: ABC是直角三角形.
理由如下:
∵,,,
,
∴
∴ ABC是直角三角形,.
22.(1)解:过点B作于点D,
在中,,设,则,
在中,,
则,,
由得,
解得,
,
答:港口A到海岛B的距离为海里;
(2)解:甲船看见灯塔所用时间:小时,
乙船看见灯塔所用时间:小时,
所以乙船先看见灯塔.
23.解:∵在中,,,,
∴,
以为直径半圆的面积:;
以为直径半圆的面积:;
以为直径半圆的面积:;
的面积为:,
∴阴影部分的面积为:.
24.(1)解:依题意,正方形纸片A的边长为;
则截出的正方形纸片B的边长为,
则原长方形纸片的长为,宽为,
∴,
故答案为:
(2)解:阴影部分的长正方形纸片A的边长,
即阴影部分的长为,
则
∴阴影部分的宽为,
∴阴影部分的面积.
(3)解:不能截出,理由如下:
∵面积为的正方形纸片的边长为,
则,
∴不能在矩形纸片上裁出两块面积是的正方形纸片.
25.(1)解:在中,米,米,
∴根据勾股定理,(米),
答:云梯顶端与墙角的距离的长为米;
(2)(米),
在中,(米),
(米),
答:云梯底端在水平方向上滑动的距离约为米.
26.(1)解:∵,
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)解:∵,
∴,
∴,
∵,其中x是整数,且,
∴,,
∴,
∴的相反数是.
27.(1)证明:∵四边形是矩形,
∴,
由折叠的性质可得,
∴,
∴四边形是矩形,
又∵,
∴四边形是正方形;
(2)解;,证明如下:
如图所示,连接,
由折叠的性质可得,
∴,
又∵,
∴ ,
∴;
(3)解:∵四边形是正方形,
∴,
设,则,
由折叠的性质可得,
∴,
在中,由勾股定理得,
∴,
解得,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题(共30分)
1.(本题3分)下列各式中,从左向右变形正确的是( )
A. B.
C. D.
2.(本题3分)如图,已知△ABC中,AB=,AC=3,BC=1,AB的垂直平分线分别交AC,AB于点D,E,连接BD,则CD的长为( )
A. B. C.1 D.
3.(本题3分)如图,矩形的对角线相交于点,过点作,交于点,连接,若,则的度数是( )
A. B. C. D.
4.(本题3分)若k,m,n都是整数,且=k,=15,=6,则下列关于k,m,n的大小关系,正确的是( )
A.m<k<n B.m=n>k C.m<n<k D.k<m=n
5.(本题3分)如图,在 ABC中,,,,以点为圆心,适当长为半径画弧,分别交,于点,,再分别以点,为圆心,大于的长为半径画弧,两弧相交于点,作射线交于点,则线段的长为( )
A.3 B. C. D.
6.(本题3分)如图,正方形的边长为1,其面积标记为,以为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为,……,按照此规律继续下去,则的值为( )
A. B. C. D.
7.(本题3分)如图,矩形中,为中点,过点的直线分别与、交于点、,连接交于点,连接、.若,,则下列结论:①,;②;③四边形是菱形;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
8.(本题3分)如图,矩形中,点、在上,将 BCF,分别沿着,翻折,点的对应点和点的对应点恰好重合在点处,则的值是( )
A. B. C. D.
9.(本题3分)如图,在 ABC中,,点D在上,且,点E和点F分别是和的中点,则的长是( )
A.3 B.4 C.5 D.6
10.(本题3分)如图,有一块直角三角形纸片,两直角边,,现将直角边沿折叠,使它落在斜边上,则等于( )
A. B. C. D.
二、填空题(共24分)
11.(本题3分)若二次根式有意义,则的取值范围为 .
12.(本题3分)如图,菱形的边长为,,,则 BDE的面积为 .
13.(本题3分)如图,中,,,,点P为上一个动点,以为轴折叠得到,点A的对应点为点Q,当点Q落在内部上时,的取值范围为 .
14.(本题3分)如图,在平行四边形中,点是中点,连接并延长交的延长线于点. 若,,的度数= .
15.(本题3分)如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,大正方形的面积为41,小正方形的面积为1,设直角三角形较短直角边长为a,较长直角边长为b,则的值为 .
16.(本题3分)E,F分别是正方形边,上的点,.以,为边作,连结并延长交于点H,连结.若,则的长为 .
17.(本题3分)如图,把长方形沿直线向上折叠,使点C落在的位置上,已知,,则 .
18.(本题3分)小明将4个全等的直角三角形拼成如图所示的五边形,添加适当的辅助线后,用等面积法建立等式证明勾股定理.小明在证题中用两种方法表示五边形的面积,分别是S1= ,S2= .
三、解答题(共66分)
19.(本题8分)计算.
(1)
(2)
20.(本题6分)已知都是实数,且,求的值.
21.(本题6分)已知:,,满足.
(1)求,,的值;
(2)请判断以,,为边构成的 ABC的形状,并说明理由.
22.(本题6分)如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东方向开往B岛,其速度仍为20海里/小时.
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?(结果保留一位小数)
23.(本题8分)如图,在中,,分别以各边为直径作半圆,图中阴影部分在数学史上被称为“希波克拉底月牙”.当,时,求阴影部分的面积.
24.(本题8分)现有两块同样大小的长方形纸片,小星采用如图①所示的方式,在长方形纸片上裁出两块面积分别为和的正方形纸片A,B.
(1)原长方形纸片的周长是_____ (结果化为最简二次根式);
(2)写出图①中阴影部分的长和宽,并求出它的面积;
(3)小红想采用如图②所示的方式,在长方形纸片上裁出面积为的两块正方形纸片,请你判断能否裁出,并说明理由.
25.(本题8分)每年的11月9日是我国的消防日,为了增强全民的消防安全意识,某校师生在消防日举行了消防演练.如图,云梯长为10米,云梯顶端靠在教学楼外墙上(墙与地面垂直),云梯底端与墙角的距离为6米.(结果保留1位小数,参考数据:,,)
(1)求云梯顶端与墙角的距离的长;
(2)假如云梯顶端下方3米处发生火灾,需将云梯顶端下滑到着火点处,则云梯底端在水平方向上滑动的距离为多少米.
26.(本题8分)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
∵,即,
∴的整数部分为2,小数部分为.请解答:
(1)的整数部分是 ,小数部分是 .
(2)已知:,其中x是整数,且,求的相反数.
27.(本题8分)如图①,在矩形纸片中,,.
【实践操作】
第一步:如图②,将图①中的矩形纸片沿过点A的直线折叠,使点D落在上的点E处,折痕为,然后把纸片展平;
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为,然后展平,隐去;
第三步:如图④,将图③中的矩形纸片沿折叠,得到,延长与交于点N,与交于点M.
【问题解决】
(1)在图②中证明四边形是正方形;
(2)请在图④中判断与的数量关系,并加以证明;
(3)请在图④中求的长度.
试卷第1页,共3页
试卷第1页,共3页
《2025春甘肃省武威第二十中学八年级数学下册人教版期中模拟试卷》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A B A A D B C D B D
11.
12.
13.
14.
15.9
16.
17.
18.
19.(1)解:
;
(2)解:
.
20.解:∵,
∴得
∴.
则,
当时,.
21.(1)解:∵,,,
又,
∴,
∴,,
(2)解: ABC是直角三角形.
理由如下:
∵,,,
,
∴
∴ ABC是直角三角形,.
22.(1)解:过点B作于点D,
在中,,设,则,
在中,,
则,,
由得,
解得,
,
答:港口A到海岛B的距离为海里;
(2)解:甲船看见灯塔所用时间:小时,
乙船看见灯塔所用时间:小时,
所以乙船先看见灯塔.
23.解:∵在中,,,,
∴,
以为直径半圆的面积:;
以为直径半圆的面积:;
以为直径半圆的面积:;
的面积为:,
∴阴影部分的面积为:.
24.(1)解:依题意,正方形纸片A的边长为;
则截出的正方形纸片B的边长为,
则原长方形纸片的长为,宽为,
∴,
故答案为:
(2)解:阴影部分的长正方形纸片A的边长,
即阴影部分的长为,
则
∴阴影部分的宽为,
∴阴影部分的面积.
(3)解:不能截出,理由如下:
∵面积为的正方形纸片的边长为,
则,
∴不能在矩形纸片上裁出两块面积是的正方形纸片.
25.(1)解:在中,米,米,
∴根据勾股定理,(米),
答:云梯顶端与墙角的距离的长为米;
(2)(米),
在中,(米),
(米),
答:云梯底端在水平方向上滑动的距离约为米.
26.(1)解:∵,
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)解:∵,
∴,
∴,
∵,其中x是整数,且,
∴,,
∴,
∴的相反数是.
27.(1)证明:∵四边形是矩形,
∴,
由折叠的性质可得,
∴,
∴四边形是矩形,
又∵,
∴四边形是正方形;
(2)解;,证明如下:
如图所示,连接,
由折叠的性质可得,
∴,
又∵,
∴ ,
∴;
(3)解:∵四边形是正方形,
∴,
设,则,
由折叠的性质可得,
∴,
在中,由勾股定理得,
∴,
解得,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
