人教版九年级数学上册 24.3 正多边形和圆 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.3 正多边形和圆 课时练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 779.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 08:46:51 | ||
图片预览


文档简介
九年级数学上册人教版第二十四章第3节《正多边形和圆》课时练习
一、单选题
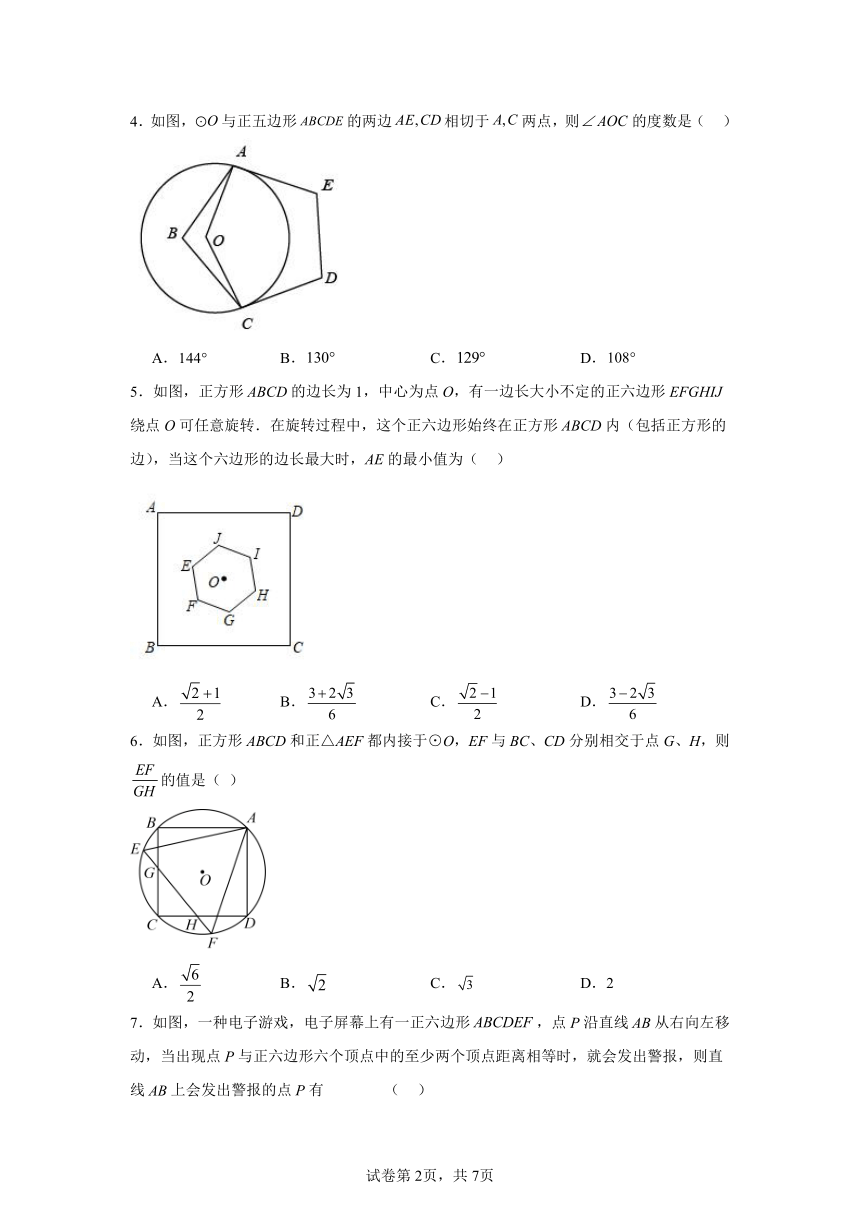
1.如图,四边形ABCD是园内接四边形,E是BC延长线上一点,若∠BAD=110°,则∠DCE的大小是( )
A.70° B.105° C.110° D.120°
2.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
3.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
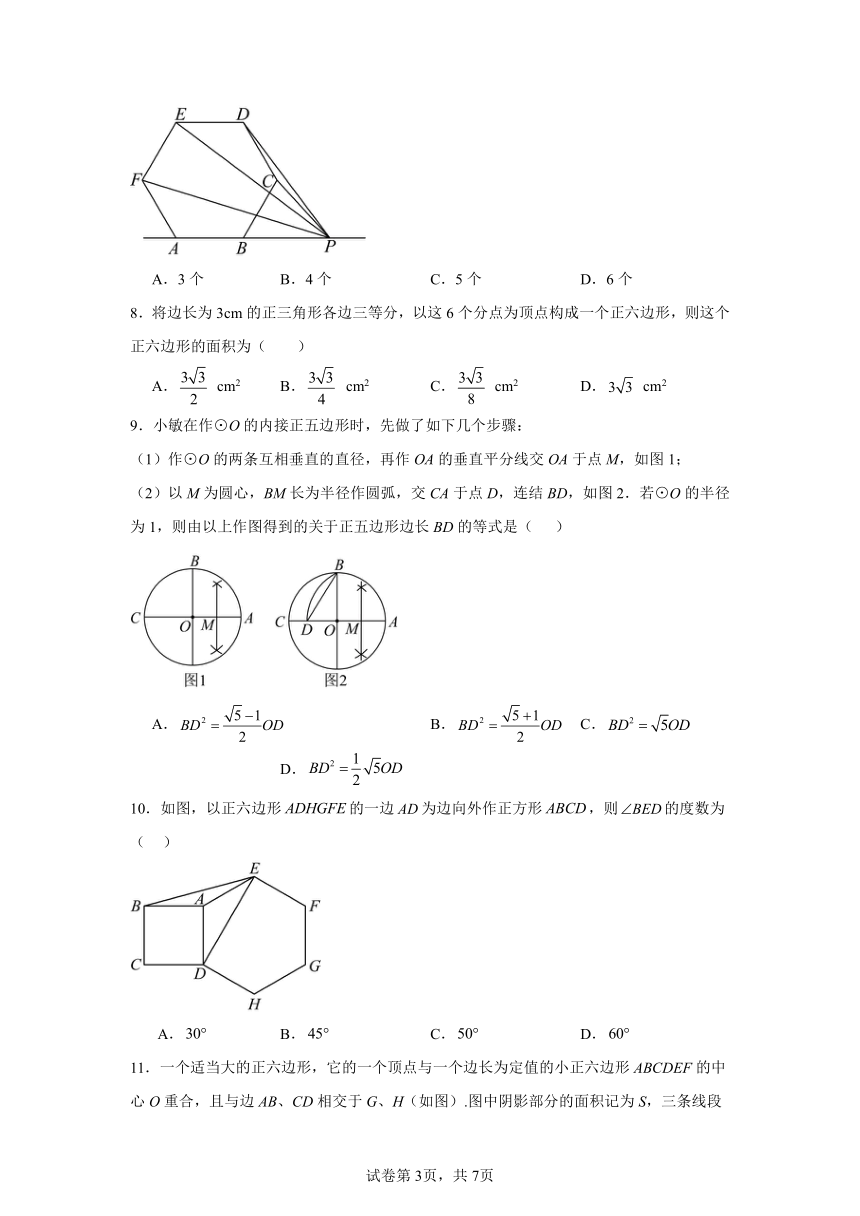
4.如图,与正五边形的两边相切于两点,则的度数是( )
A. B. C. D.
5.如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转.在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
A. B. C. D.
6.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A. B. C. D.2
7.如图,一种电子游戏,电子屏幕上有一正六边形,点P沿直线从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线上会发出警报的点P有 ( )
A.3个 B.4个 C.5个 D.6个
8.将边长为3cm的正三角形各边三等分,以这6个分点为顶点构成一个正六边形,则这个正六边形的面积为( )
A. cm2 B. cm2 C. cm2 D. cm2
9.小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A. B. C. D.
10.如图,以正六边形的一边为边向外作正方形,则的度数为( )
A. B. C. D.
11.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,大正六边形在绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
二、填空题
12.如图,点O是正五边形的中心,连接,则的度数为 .
13.T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=;③a:b=1:;④S1:S2=3:4.其中正确的有 .(填序号)
14.如图,已知为直径,若是内接正边形的一边,是内接正边形的一边,,则 .
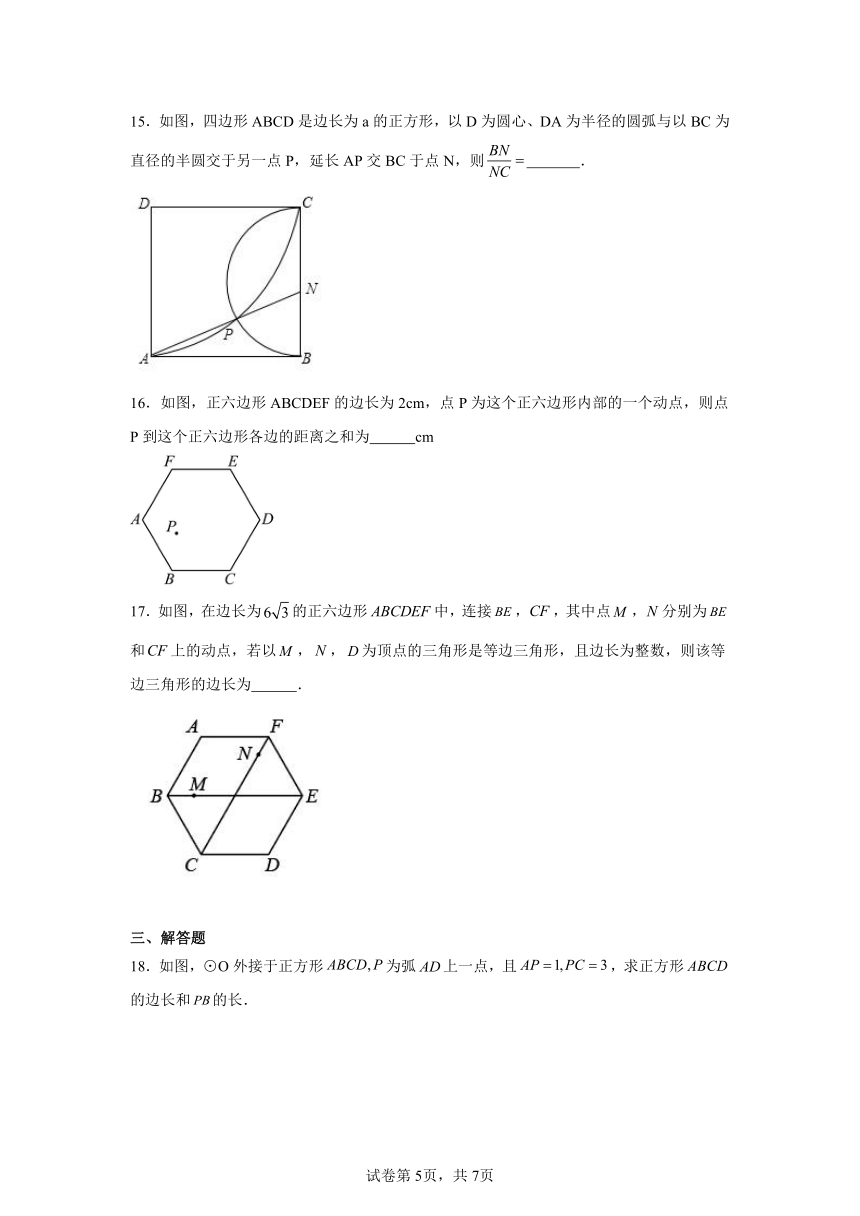
15.如图,四边形ABCD是边长为a的正方形,以D为圆心、DA为半径的圆弧与以BC为直径的半圆交于另一点P,延长AP交BC于点N,则 .
16.如图,正六边形ABCDEF的边长为2cm,点P为这个正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为 cm
17.如图,在边长为的正六边形中,连接,,其中点,分别为和上的动点,若以,,为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .
三、解答题
18.如图,⊙O外接于正方形为弧上一点,且,求正方形的边长和的长.
19.如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
(1)求证:△CDP≌△POB;
(2)填空:
①若AB=4,则四边形AOPD的最大面积为_______,此时BD=_______;
②连接OD,当∠PBA的度数为________时,四边形BPDO是菱形.
20.请用无刻度直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果).
(1)如图1,E是平行四边形ABCD边AD上一点,过点A画一条直线,使其与EC平行;
(2)如图2,正六边形ABCDEF(六边相等,六角相等的六边形),在图中画一条直线,使其垂直平分AF;
(3)如图3,⊙O是四边形ABCD的外接圆,且AB=BC=CD,在图中画一条异于BC的直线,使其与AD平行.
21.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
22.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形中,在、边上分别取点M、N,使,连接、,发现,试说明:.
(2)如图2,正方形中,在、边上分别取点M、N,使,连接、,那么______度,并说明理由.
(3)如图3,正五边形中,在、边上分别取点M、N,使,连接、,那么______,且______度.(正n边形内角和,正多边形各内角相等)
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第3节《正多边形和圆》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A C C C A C B
题号 11
答案 D
12.18
13.①②④
14.
15.
16.6
17.9或10或18
18.解:连接,作于点,
如图所示.
∵四边形是正方形,
,
是的直径,ΔABC是等腰直角三角形,
是等腰直角三角形,
,
.
正方形的边长为的长为.
19.(1)证明:∵PC=PB,D是AC的中点,
∴DP∥AB,
∴DP=AB,∠CPD=∠PBO,
∵BO=AB,
∴DP=BO,
在△CDP与△POB中,
∴△CDP≌△POB(SAS);
(2)①当四边形AOPD的AO边上的高等于半径时有最大面积,
(4÷2)×(4÷2)
=2×2
=4;
BD==
②如图:
∵DP∥AB,DP=BO,
∴四边形BPDO是平行四边形,
∵四边形BPDO是菱形,
∴PB=BO,
∵PO=BO,
∴PB=BO=PO,
∴△PBO是等边三角形,
∴∠PBA的度数为60°.
20.解:(1)如图1,直线AF即为所求作.
(2)如图2,直线GH即为所求作.
(3)如图3,直线EF即为所求作.
21.(1)如图,连接OB、OC,则,
是内接正三角形,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
22.(1)证明:∵ΔABC是正三角形,
∴,,
在和中,
,
∴,
∴,,
又∵,
∴,
∴;
(2)解:∵四边形是正方形,
∴,,
又∵,
∴,
∴,
又∵,
∴,
∴;
即;
(3)解:∵五边形是正五边形,
∴,,
又∵,
∴,
∴,,
∴.
故答案为:,.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,四边形ABCD是园内接四边形,E是BC延长线上一点,若∠BAD=110°,则∠DCE的大小是( )
A.70° B.105° C.110° D.120°
2.如图,四边形内接于⊙O ,,那么等于( )
A.110° B.135° C.55° D.125°
3.如图,在正方形ABCD中,AB=12,点E为BC的中点,以CD为直径作半圆CFD,点F为半圆的中点,连接AF,EF,图中阴影部分的面积是( )
A.18+36π B.24+18π C.18+18π D.12+18π
4.如图,与正五边形的两边相切于两点,则的度数是( )
A. B. C. D.
5.如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转.在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个六边形的边长最大时,AE的最小值为( )
A. B. C. D.
6.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则的值是( )
A. B. C. D.2
7.如图,一种电子游戏,电子屏幕上有一正六边形,点P沿直线从右向左移动,当出现点P与正六边形六个顶点中的至少两个顶点距离相等时,就会发出警报,则直线上会发出警报的点P有 ( )
A.3个 B.4个 C.5个 D.6个
8.将边长为3cm的正三角形各边三等分,以这6个分点为顶点构成一个正六边形,则这个正六边形的面积为( )
A. cm2 B. cm2 C. cm2 D. cm2
9.小敏在作⊙O的内接正五边形时,先做了如下几个步骤:
(1)作⊙O的两条互相垂直的直径,再作OA的垂直平分线交OA于点M,如图1;
(2)以M为圆心,BM长为半径作圆弧,交CA于点D,连结BD,如图2.若⊙O的半径为1,则由以上作图得到的关于正五边形边长BD的等式是( )
A. B. C. D.
10.如图,以正六边形的一边为边向外作正方形,则的度数为( )
A. B. C. D.
11.一个适当大的正六边形,它的一个顶点与一个边长为定值的小正六边形ABCDEF的中心O重合,且与边AB、CD相交于G、H(如图).图中阴影部分的面积记为S,三条线段GB、BC、CH的长度之和记为l,大正六边形在绕点O旋转过程中,下列说法正确的是( )
A.S变化,l不变 B.S不变,l变化
C.S变化,l变化 D.S与l均不变
二、填空题
12.如图,点O是正五边形的中心,连接,则的度数为 .
13.T1、T2分别为⊙O的内接正六边形和外切正六边形.设T1的半径r,T1、T2的边长分别为a、b,T1、T2的面积分别为S1、S2.下列结论:①r:a=1:1;②r:b=;③a:b=1:;④S1:S2=3:4.其中正确的有 .(填序号)
14.如图,已知为直径,若是内接正边形的一边,是内接正边形的一边,,则 .
15.如图,四边形ABCD是边长为a的正方形,以D为圆心、DA为半径的圆弧与以BC为直径的半圆交于另一点P,延长AP交BC于点N,则 .
16.如图,正六边形ABCDEF的边长为2cm,点P为这个正六边形内部的一个动点,则点P到这个正六边形各边的距离之和为 cm
17.如图,在边长为的正六边形中,连接,,其中点,分别为和上的动点,若以,,为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .
三、解答题
18.如图,⊙O外接于正方形为弧上一点,且,求正方形的边长和的长.
19.如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO.
(1)求证:△CDP≌△POB;
(2)填空:
①若AB=4,则四边形AOPD的最大面积为_______,此时BD=_______;
②连接OD,当∠PBA的度数为________时,四边形BPDO是菱形.
20.请用无刻度直尺完成下列作图,不写画法,保留画图痕迹(用虚线表示画图过程,实线表示画图结果).
(1)如图1,E是平行四边形ABCD边AD上一点,过点A画一条直线,使其与EC平行;
(2)如图2,正六边形ABCDEF(六边相等,六角相等的六边形),在图中画一条直线,使其垂直平分AF;
(3)如图3,⊙O是四边形ABCD的外接圆,且AB=BC=CD,在图中画一条异于BC的直线,使其与AD平行.
21.如图M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDEFG…的边AB、BC上的点,且BM=CN,连接OM、ON
(1)求图1中∠MON的度数
(2)图2中∠MON的度数是 ,图3中∠MON的度数是
(3)试探究∠MON的度数与正n边形边数n的关系是____
22.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形中,在、边上分别取点M、N,使,连接、,发现,试说明:.
(2)如图2,正方形中,在、边上分别取点M、N,使,连接、,那么______度,并说明理由.
(3)如图3,正五边形中,在、边上分别取点M、N,使,连接、,那么______,且______度.(正n边形内角和,正多边形各内角相等)
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第3节《正多边形和圆》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A C C C A C B
题号 11
答案 D
12.18
13.①②④
14.
15.
16.6
17.9或10或18
18.解:连接,作于点,
如图所示.
∵四边形是正方形,
,
是的直径,ΔABC是等腰直角三角形,
是等腰直角三角形,
,
.
正方形的边长为的长为.
19.(1)证明:∵PC=PB,D是AC的中点,
∴DP∥AB,
∴DP=AB,∠CPD=∠PBO,
∵BO=AB,
∴DP=BO,
在△CDP与△POB中,
∴△CDP≌△POB(SAS);
(2)①当四边形AOPD的AO边上的高等于半径时有最大面积,
(4÷2)×(4÷2)
=2×2
=4;
BD==
②如图:
∵DP∥AB,DP=BO,
∴四边形BPDO是平行四边形,
∵四边形BPDO是菱形,
∴PB=BO,
∵PO=BO,
∴PB=BO=PO,
∴△PBO是等边三角形,
∴∠PBA的度数为60°.
20.解:(1)如图1,直线AF即为所求作.
(2)如图2,直线GH即为所求作.
(3)如图3,直线EF即为所求作.
21.(1)如图,连接OB、OC,则,
是内接正三角形,
∵点O是内接正三角形ABC的内心,
∴,
∴,
在和中,,
∴,
∴,
∴,
故答案为:;
(2)如图1,连接OB、OC,
四边形ABCD是内接正方形,
中心角,
同(1)的方法可证:;
如图2,连接OB、OC,
五边形ABCDE是内接正五边形,
中心角,
同(1)的方法可证:,
故答案为:,;
(3)由上可知,的度数与正三角形边数的关系是,
的度数与正方形边数的关系是,
的度数与正五边形边数的关系是,
归纳类推得:的度数与正n边形边数n的关系是,
故答案为:.
22.(1)证明:∵ΔABC是正三角形,
∴,,
在和中,
,
∴,
∴,,
又∵,
∴,
∴;
(2)解:∵四边形是正方形,
∴,,
又∵,
∴,
∴,
又∵,
∴,
∴;
即;
(3)解:∵五边形是正五边形,
∴,,
又∵,
∴,
∴,,
∴.
故答案为:,.
答案第1页,共2页
答案第1页,共2页
同课章节目录
