人教版九年级数学上册 24.4 弧长和扇形面积 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.4 弧长和扇形面积 课时练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 798.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 08:51:00 | ||
图片预览




文档简介
九年级数学上册人教版第二十四章第4节《弧长和扇形面积》课时练习
一、单选题
1.若扇形的圆心角为45°,半径为6,则扇形的弧长为( )
A. B. C. D.
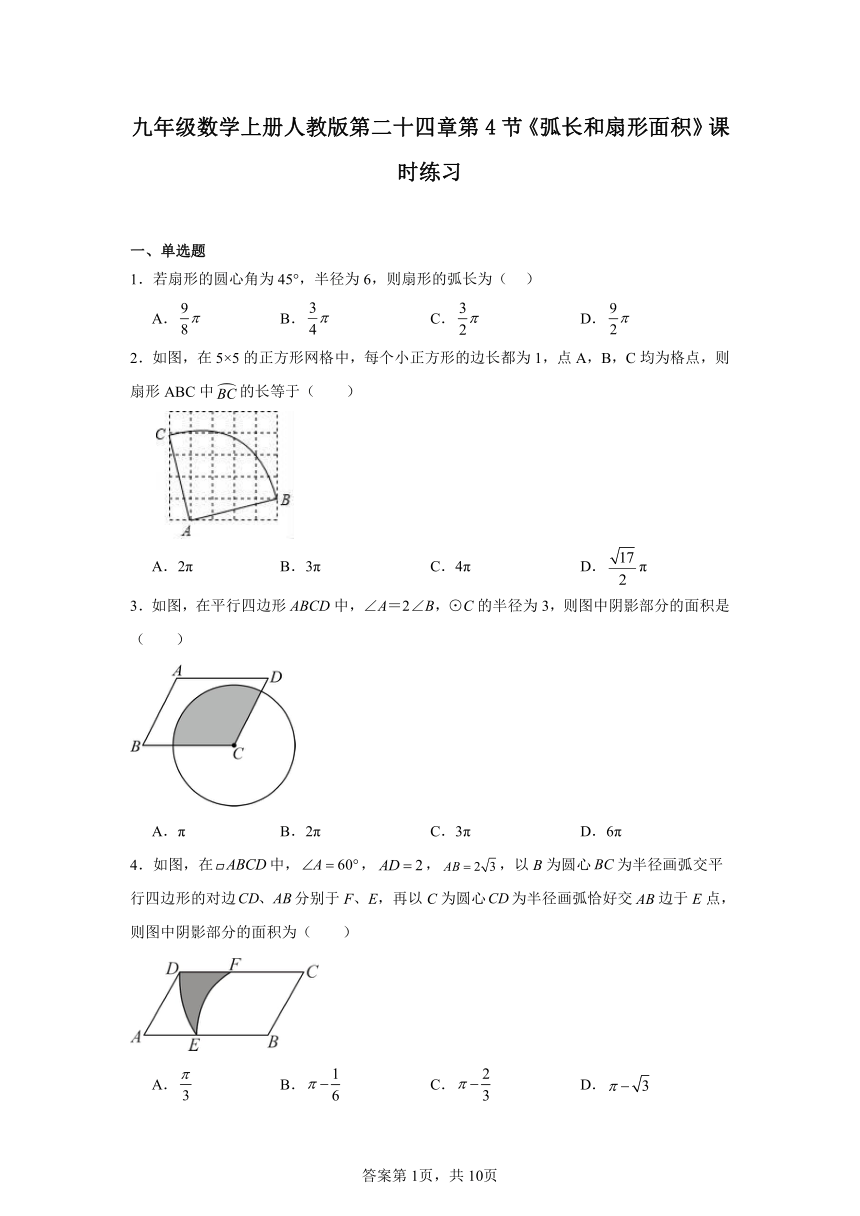
2.如图,在5×5的正方形网格中,每个小正方形的边长都为1,点A,B,C均为格点,则扇形ABC中的长等于( )
A.2π B.3π C.4π D.π
3.如图,在平行四边形ABCD中,∠A=2∠B,⊙C的半径为3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
4.如图,在中,,,,以B为圆心为半径画弧交平行四边形的对边分别于F、E,再以C为圆心为半径画弧恰好交边于E点,则图中阴影部分的面积为( )
A. B. C. D.
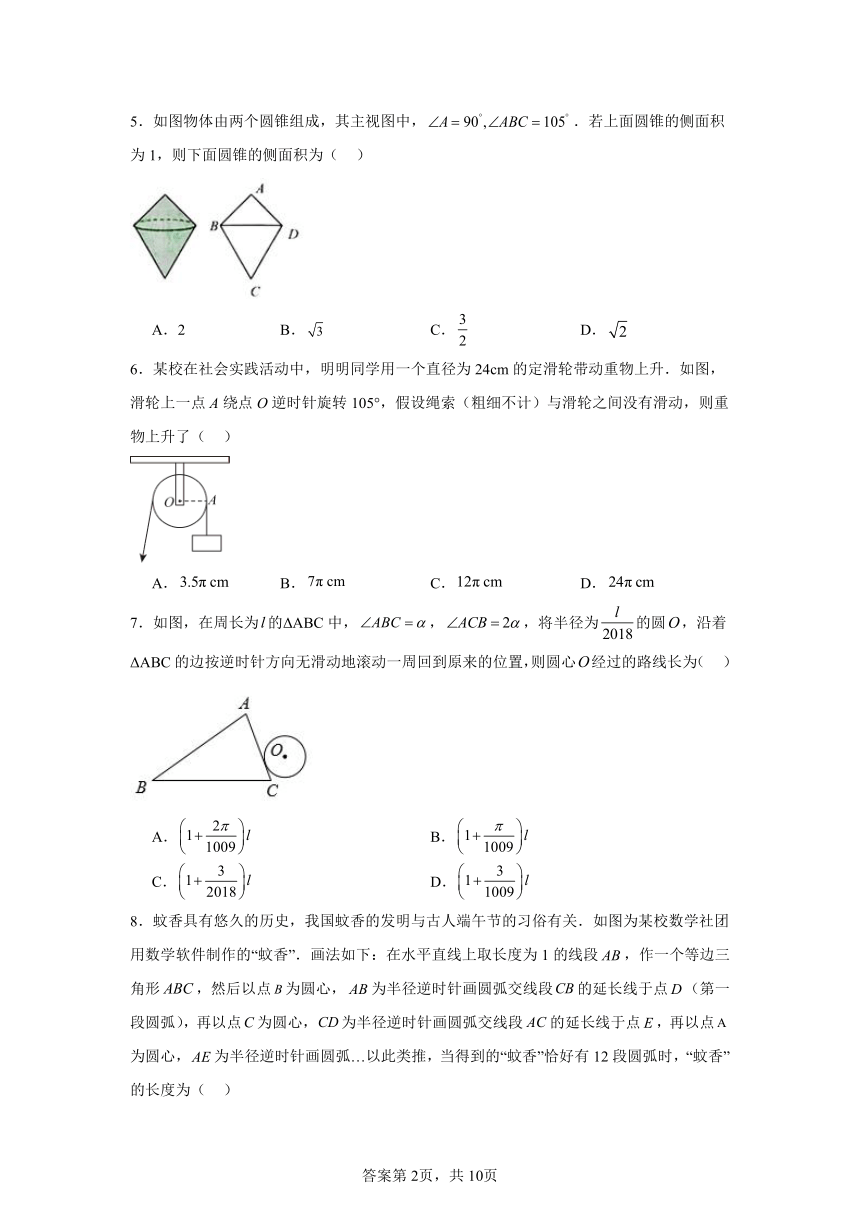
5.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B. C. D.
6.某校在社会实践活动中,明明同学用一个直径为24cm的定滑轮带动重物上升.如图,滑轮上一点A绕点O逆时针旋转105°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A. B. C. D.
7.如图,在周长为的ΔABC中,,,将半径为的圆,沿着ΔABC的边按逆时针方向无滑动地滚动一周回到原来的位置,则圆心经过的路线长为( )
A. B.
C. D.
8.蚊香具有悠久的历史,我国蚊香的发明与古人端午节的习俗有关.如图为某校数学社团用数学软件制作的“蚊香”.画法如下:在水平直线上取长度为1的线段,作一个等边三角形,然后以点为圆心,为半径逆时针画圆弧交线段的延长线于点(第一段圆弧),再以点为圆心,为半径逆时针画圆弧交线段的延长线于点,再以点为圆心,为半径逆时针画圆弧…以此类推,当得到的“蚊香”恰好有12段圆弧时,“蚊香”的长度为( )
A. B. C. D.
9.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即的长为( )
A. B. C. D.
10.传统服饰日益受到关注,如图①为明清时期女子主要裙式之一的马面裙,如图②马面裙可以近似地看作扇形的一部分,其中的长度为米,裙长米,圆心角,则的长为( )
A.1米 B.米 C.2米 D.米
二、填空题
11.如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则= ;线段AB扫过的图形(阴影部分)的面积为 .
12.如图,的半径为,是弦,以点为圆心,为半径画弧,交于点,若,则阴影部分的面积为 .
13.如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为 .(结果保留π)
14.如图所示,在的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.,,分别是小正方形的顶点,则的长等于 .(结果保留根号及).
15.如图,在边长为2的正方形中,是以为直径的半圆的切线,则图中阴影部分的面积为 .
16.如图,在RtΔABC中,∠C=90°,∠A=30°,AB=2.将ΔABC绕顶点A顺时针方向旋转至的位置,B,A,三点共线,则线段BC扫过的区域面积为 .
17.如图,一块六边形绿化园地,六个角处都建有半径为的圆形喷水池,则这六个喷水池占去的绿化园地的面积(图中阴影部分)为 (结果保留)
18.如图1是小明制作的一副弓箭,点A,D分别是弓臂与弓弦的中点,弓弦,沿方向拉动弓弦的过程中,假设弓臂始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点时,有,.
(1)图2中,弓臂两端,的距离为 .
(2)如图3,将弓箭继续拉到点,使弓臂为半圆,则的长为 .
三、解答题
19.如图,在中,.延长到O,使,以O 为圆心,长为半径作交延长线于点D,连结.
(1)求扇形的面积.
(2)判断所在直线与的位置关系,并说明理由.
20.如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)∠C=45°,⊙O的半径为2,求阴影部分面积.
21.如图,已知点A,B,C均在上,点D是AC的中点.
(1)请仅用无刻度的直尺画出的平分线BE交于点E;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,半径为3,求弧EC的长.
22.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
《九年级数学上册人教版第二十四章第4节《弧长和扇形面积》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A D B B B D B
11. /
12.
13.
14.
15.
16./
17.
18.
19.(1)在中,,
∴,.
∴.
∵,
∴是等边三角形.
∴.
∴.
(2)所在直线与相切.
理由:∵是等边三角形,
∴.
∵,
∴.
∴.
∴,即.
∵为的半径,
∴所在直线与相切.
20.解:(1)连接OE.
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,
∴∠ADC=90°,
故∠OEC=90°.
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵∠C=45°,
∴△OCE是等腰直角三角形,
∴CE=OE=2,∠COE=45°,
∴阴影部分面积=S△OCE﹣S扇形OBE=2×2﹣=2﹣.
21.(1)连接OD,交⊙O于点E,连接BE,
则BE就是我们所要作的图形.
(2)∵BE平分∠ABC,
∴,
∴,
∴.
22.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OFBC;
(2)证明:∵AB⊥CD,
∴,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OFBC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB(AAS);
∴
,
是等边三角形,
,
,
,
∴∠COD=120°,
∴扇形COD的面积是:,
由垂径定理可得:
∴
∴
∴阴影部分面积为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若扇形的圆心角为45°,半径为6,则扇形的弧长为( )
A. B. C. D.
2.如图,在5×5的正方形网格中,每个小正方形的边长都为1,点A,B,C均为格点,则扇形ABC中的长等于( )
A.2π B.3π C.4π D.π
3.如图,在平行四边形ABCD中,∠A=2∠B,⊙C的半径为3,则图中阴影部分的面积是( )
A.π B.2π C.3π D.6π
4.如图,在中,,,,以B为圆心为半径画弧交平行四边形的对边分别于F、E,再以C为圆心为半径画弧恰好交边于E点,则图中阴影部分的面积为( )
A. B. C. D.
5.如图物体由两个圆锥组成,其主视图中,.若上面圆锥的侧面积为1,则下面圆锥的侧面积为( )
A.2 B. C. D.
6.某校在社会实践活动中,明明同学用一个直径为24cm的定滑轮带动重物上升.如图,滑轮上一点A绕点O逆时针旋转105°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A. B. C. D.
7.如图,在周长为的ΔABC中,,,将半径为的圆,沿着ΔABC的边按逆时针方向无滑动地滚动一周回到原来的位置,则圆心经过的路线长为( )
A. B.
C. D.
8.蚊香具有悠久的历史,我国蚊香的发明与古人端午节的习俗有关.如图为某校数学社团用数学软件制作的“蚊香”.画法如下:在水平直线上取长度为1的线段,作一个等边三角形,然后以点为圆心,为半径逆时针画圆弧交线段的延长线于点(第一段圆弧),再以点为圆心,为半径逆时针画圆弧交线段的延长线于点,再以点为圆心,为半径逆时针画圆弧…以此类推,当得到的“蚊香”恰好有12段圆弧时,“蚊香”的长度为( )
A. B. C. D.
9.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即的长为( )
A. B. C. D.
10.传统服饰日益受到关注,如图①为明清时期女子主要裙式之一的马面裙,如图②马面裙可以近似地看作扇形的一部分,其中的长度为米,裙长米,圆心角,则的长为( )
A.1米 B.米 C.2米 D.米
二、填空题
11.如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,BC=2,则= ;线段AB扫过的图形(阴影部分)的面积为 .
12.如图,的半径为,是弦,以点为圆心,为半径画弧,交于点,若,则阴影部分的面积为 .
13.如图,圆锥的主视图是一个等腰直角三角形,直角边长为2,则这个圆锥的侧面积为 .(结果保留π)
14.如图所示,在的方格纸中(共有16个小方格),每个小方格都是边长为1的正方形.,,分别是小正方形的顶点,则的长等于 .(结果保留根号及).
15.如图,在边长为2的正方形中,是以为直径的半圆的切线,则图中阴影部分的面积为 .
16.如图,在RtΔABC中,∠C=90°,∠A=30°,AB=2.将ΔABC绕顶点A顺时针方向旋转至的位置,B,A,三点共线,则线段BC扫过的区域面积为 .
17.如图,一块六边形绿化园地,六个角处都建有半径为的圆形喷水池,则这六个喷水池占去的绿化园地的面积(图中阴影部分)为 (结果保留)
18.如图1是小明制作的一副弓箭,点A,D分别是弓臂与弓弦的中点,弓弦,沿方向拉动弓弦的过程中,假设弓臂始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点时,有,.
(1)图2中,弓臂两端,的距离为 .
(2)如图3,将弓箭继续拉到点,使弓臂为半圆,则的长为 .
三、解答题
19.如图,在中,.延长到O,使,以O 为圆心,长为半径作交延长线于点D,连结.
(1)求扇形的面积.
(2)判断所在直线与的位置关系,并说明理由.
20.如图,AB是⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
(1)求证:CD是⊙O的切线;
(2)∠C=45°,⊙O的半径为2,求阴影部分面积.
21.如图,已知点A,B,C均在上,点D是AC的中点.
(1)请仅用无刻度的直尺画出的平分线BE交于点E;(保留作图痕迹,不写作法)
(2)在(1)的条件下,若,半径为3,求弧EC的长.
22.如图,已知AB为⊙O的直径,CD是弦,AB⊥CD于E,OF⊥AC于F,BE=OF.
(1)求证:.
(2)求证:△AFO≌△CEB.
(3)若EB=5cm,设OE=x,求x值及阴影部分的面积.
《九年级数学上册人教版第二十四章第4节《弧长和扇形面积》课时练习》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C A D B B B D B
11. /
12.
13.
14.
15.
16./
17.
18.
19.(1)在中,,
∴,.
∴.
∵,
∴是等边三角形.
∴.
∴.
(2)所在直线与相切.
理由:∵是等边三角形,
∴.
∵,
∴.
∴.
∴,即.
∵为的半径,
∴所在直线与相切.
20.解:(1)连接OE.
∵OA=OE,
∴∠OAE=∠OEA,
又∵∠DAE=∠OAE,
∴∠OEA=∠DAE,
∴OE∥AD,
∴∠ADC=∠OEC,
∵AD⊥CD,
∴∠ADC=90°,
故∠OEC=90°.
∴OE⊥CD,
∴CD是⊙O的切线;
(2)∵∠C=45°,
∴△OCE是等腰直角三角形,
∴CE=OE=2,∠COE=45°,
∴阴影部分面积=S△OCE﹣S扇形OBE=2×2﹣=2﹣.
21.(1)连接OD,交⊙O于点E,连接BE,
则BE就是我们所要作的图形.
(2)∵BE平分∠ABC,
∴,
∴,
∴.
22.(1)证明:∵AB为⊙O的直径,
∴AC⊥BC,
又∵OF⊥AC,
∴OFBC;
(2)证明:∵AB⊥CD,
∴,
∴∠CAB=∠BCD,
在△AFO和△CEB中,
∴△AFO≌△CEB(AAS);
(3)解:连接DO.设OE=x,
∵OFBC,OA=OB,
∴OF=BC,
∵OF=BE=5cm,
∴BC=10cm,
∵△AFO≌△CEB(AAS);
∴
,
是等边三角形,
,
,
,
∴∠COD=120°,
∴扇形COD的面积是:,
由垂径定理可得:
∴
∴
∴阴影部分面积为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
