人教版九年级数学下册 28.1 锐角三角函数 课时练习(含答案)
文档属性
| 名称 | 人教版九年级数学下册 28.1 锐角三角函数 课时练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览




文档简介
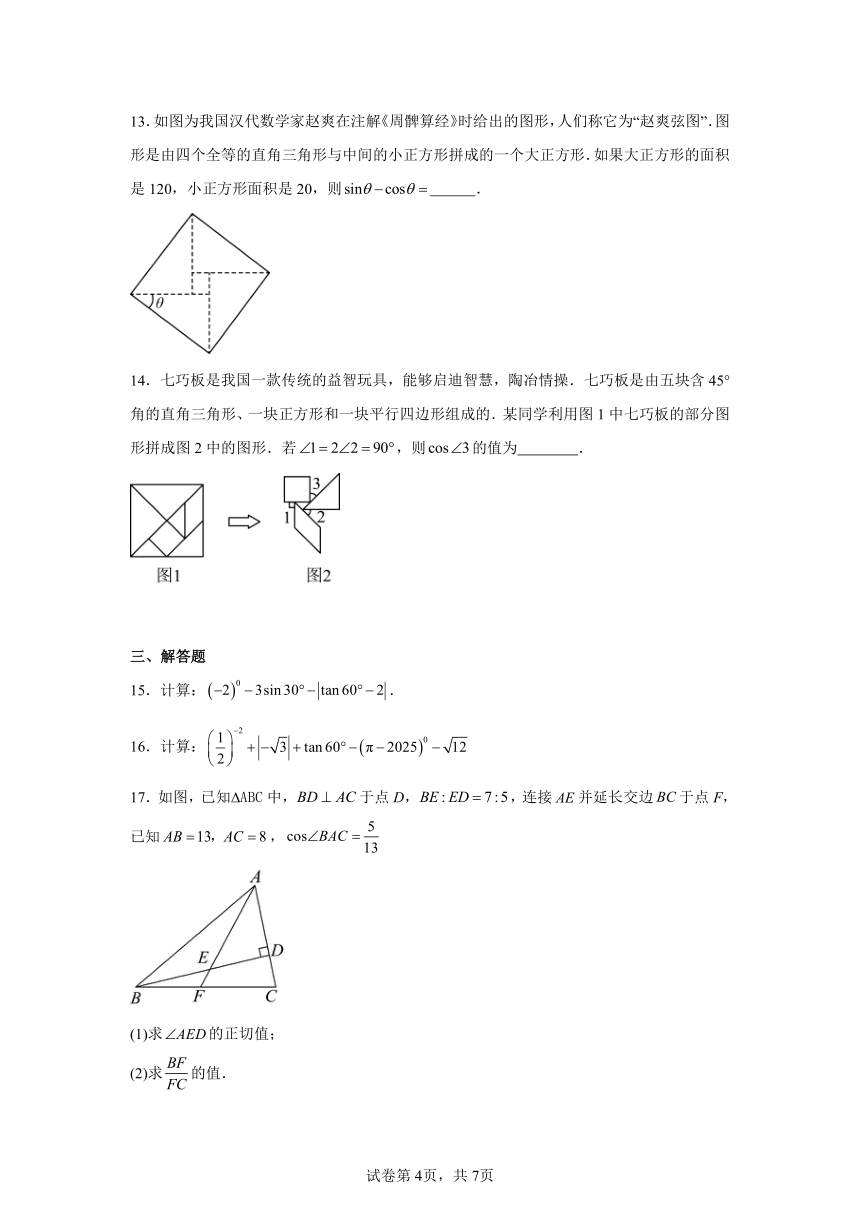
九年级数学下册人教版第二十八章第1节《锐角三角函数》课时练习
一、单选题
1.如下图所示,在矩形中,于点,设,且,,则的长为( )
A.3 B. C. D.
2.如图,在四边形中,,,以D为圆心,为半径的弧恰好与相切,切点为E,若,则的值是( )
A. B. C. D.
3.如图,中,,是斜边上的中线,过点作交于点.若的面积为25,,则的长为( )
A.6 B. C. D.10
4.因为,,所以.由此猜想,推理可知:当为锐角时,有,由此可知( )
A. B. C. D.
5.在 ABC中,若,则么 ABC一定是( )
A.锐角三角形 B.钝角三角形 C.等边三角形 D.等腰直角三角形
6.化简:的结果是
A. B.
C. D.
7.如图,在△ABC中,tan∠BACtan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
A. B.
C.13 D.
8.如图,在矩形中,,点E是边上一动点(点E不与点A重合),过点D作交的延长线于点F,以,为邻边作矩形,交于点H,连接,则下列结论:①;②当点恰好落在的延长线上时,;③当点在边上运动时,为定值;④当点在边上运动时,长度的最大值为.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在 ABC中,,点在边上,满足,若,则图中等于的角有 个.
10.如图,在矩形中,,,点是边上一点,,连接,将沿翻折,得到,延长,交的延长线于点,则 .
11.如图,在正方形中,点分别在边上.连接,若,则的正切值为 .
12.如图,已知是平行四边形的边上一点,将沿直线折叠,点落在平行四边形内的点处,且,如果,,的正弦值为,那么的长为 .
13.如图为我国汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.图形是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是120,小正方形面积是20,则 .
14.七巧板是我国一款传统的益智玩具,能够启迪智慧,陶冶情操.七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的.某同学利用图1中七巧板的部分图形拼成图2中的图形.若,则的值为 .
三、解答题
15.计算:.
16.计算:
17.如图,已知 ABC中,于点D,,连接并延长交边于点F,已知,
(1)求的正切值;
(2)求的值.
18.如图,是的直径,点为上一点,过点作的垂线,交过点的切线于点,交于点,连接交于点.
(1)求证:.
(2)若的半径为10,,求的长.
19.如图,是的外接圆,为直径,点是劣弧ED的中点,连接,,过点作交的延长线于点,使得.
(1)求证:为的切线;
(2)求证:;
(3)若的半径,,求的长度.
20.在如图的直角三角形中,我们知道,,,
∴.即一个角的正弦和余弦的平方和为1.
(1)请你根据上面的探索过程,探究,与之间的关系;
(2)请你利用上面探究的结论解答下面问题:已知为锐角,且,求的值.
21.如图,在菱形中,为锐角,是对角线上的一个动点,连接.
(1)如图,求证:;
(2)如图,在左侧作,延长分别交于点.
①当,时,求的长;
②如图,在上截取,连接交于点,连接交对角线于点,求证:四边形是平行四边形.
22.在中,,是上一点,,点在上.
(1)过点作的垂线分别交,于,.
①如图1,当时,________,________;
②如图2,若是的中点,当时,求证: ADE是等边三角形;
(2)如图3,若是的中点,,直接写出的值.
23.已知a、b、c分别是 ABC的角A、B、C的对边(),二次函数图像的顶点在x轴上,且、是关于x的方程的两个根.
(1)判断 ABC的形状;
(2)求m的值;
(3)若这个三角形的外接圆面积为,求 ABC的内接正方形的边长.
24.阅读理解:
如图①,在中,,根据锐角三角函数的定义,我们可以得出以下结论:.
(1)如图②,在矩形中,,连接,若,求的长;
(2)如图③,李叔叔有一块形状为菱形的地,其中,李叔叔想在地中间开辟一块矩形区域种植花卉,花卉四周种植树木,每棵树木相隔2m,他在上取了一点E,过点E作交于点H,过点H作交于点G,过点G作交于点F,连接,则矩形就是他想要种植花卉和树木的区域.
①在种植过程中,他发现需要种植树木的数量(单位:棵)随着长度(单位:m)的变化而变化,请完成下表:
长度/m 10 20 30 …
需要种植树木的数量/棵 …
若用y表示需要种植树木的数量,x表示AE的长度,试求出y与x的关系式;
②当矩形是正方形时,求正方形的一条边上最多可以种植多少棵树
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十八章第1节《锐角三角函数》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A B B D C C D
9.2
10.
11.
12.
13.
14.
15.解:原式
.
16.解:
17.(1)解:∵,
∴,
在中,,
∴,
由勾股定理得:,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
过D作交于点G,
∴,,
∴,
设,则,
∴.
18.(1)证明:∵是的切线,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
(2)解:连接,如图所示,
∵是的直径,的半径为10,
∴,.
∵在中,,
∴,
∴.
∵,
∴,
∴,
∴.
∵,,
∴,
∴.
设,则.
∵在中,,
∴,
∴(负值已舍去),
∴
19.(1)证明:连接,
,
,
,
为直径,
,
,
,
,
,
过半径的外端点,且,
为的切线;
(2)证明:为劣弧的中点,
,
∵,,
,
;
(3)解:过点作于点,
∵,,
∴,
∴,
∴,
∴,
∵为直径,
∴,
∴,
,
在中,,,
,
∴,
,,,
,
∴,
∴,
,
,,
,,
,
,
,
.
20.(1)解:∵,,,
∴,
∴.
(2)解:∵,且,
∴.
21.(1)证明:∵四边形是菱形,
∴,,
又∵,
∴;
(2)解:①∵,
∴,
∵,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴,
过点作于,则,,
∵,
∴,
∴,
即,
∴,
∴;
②延长至,
∵四边形是菱形,
∴,,,
∵,
∴,,
又∵,
∴,
∴,
∴,
即,
在和中,
,
∴,
∴,
在和 ADE中,
,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
即,
∵,
∴四边形是平行四边形.
22.(1)①作于,则.
由题意知:n=2,设CD=1,
∴BD=2.
在△ABC,△DCP,△ADP中
∵BD=2,CD=1,AB=AC,∠BAC=
∴AB=AC= ,DP=CP=,
∴AP=,
在△AEM和△AFM中,
∵AD⊥EF,∠BAC=
∴
∴△MAF∽△MEA
∴,∠AEM=∠FAM
又∵∠DAP=∠FAM,∠FAM=∠AEM
∴
故答案为,.
②作于,则,
,
,
,
,
,
,.
又,是的中点,
,
因为 ADE是等边三角形.
(2)作AO⊥BC,MN⊥BC分别交BC与点O,N.
由题意知:
∴∠MCB=
设AO=2.
∵点M为AD的中点,AB=AC,AO⊥BC
∴MN=AO=1,ON=ND,BO=OC=2
在△MNC中
∵∠MCB=,MN⊥BC,MN=1
∴MC=2,NC=
∴ON=OC-NC=
∵ON=ND,ON=
∴ND=,OD=
即BD=,CD=.
∴.
23.(1) ABC是直角三角形;
证明:将化简得到,
由于二次函数图像的顶点在x轴上,
,
;
故 ABC是直角三角形;
(2)解: ABC是直角三角形,,
,
,
、是关于x的方程的两个根,
,
,
,
,
整理得,
解得,
经检验,都是原方程的根,
当时,,
当时,舍去,
故;
(3)解:由于三角形的外接圆面积为,
外接圆半径,
斜边,
将代入方程得到,
解得,
,
设正方形边长为,
由,
得,
解得;
图2中,,
,
即,
解得.
综上所述, ABC的内接正方形的边长为或.
24.(1)∵角B是90度,∴,
解得.
在中,;
(2)①表格种依次填写:156,152,148;
如图,连接交于点O,交于点M,设交于点N.
∵四边形是菱形,
∴,
∴.
由菱形的对称性可知,,
∵时,.
∵,,
∴,.
∵每棵树木相隔2m,,,
所以当时,需要种植树木得数量是(棵);
同理:当时,需要种植树木得数量是152棵;
当时,需要种植树木得数量是148棵.
故答案为:156,152,148;
如图,连接交于点O,交于点M,设交于点N.
∵四边形是菱形,
∴,
∴.
由菱形的对称性可知,,
当时,,
∵,,
∴,.
∵每棵树木相隔2m,,,
∴;
②当矩形是正方形时,由题意可得,
,
解得,
此时,
∴,
∴正方形得一条边上最多可以种植35棵树.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如下图所示,在矩形中,于点,设,且,,则的长为( )
A.3 B. C. D.
2.如图,在四边形中,,,以D为圆心,为半径的弧恰好与相切,切点为E,若,则的值是( )
A. B. C. D.
3.如图,中,,是斜边上的中线,过点作交于点.若的面积为25,,则的长为( )
A.6 B. C. D.10
4.因为,,所以.由此猜想,推理可知:当为锐角时,有,由此可知( )
A. B. C. D.
5.在 ABC中,若,则么 ABC一定是( )
A.锐角三角形 B.钝角三角形 C.等边三角形 D.等腰直角三角形
6.化简:的结果是
A. B.
C. D.
7.如图,在△ABC中,tan∠BACtan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
A. B.
C.13 D.
8.如图,在矩形中,,点E是边上一动点(点E不与点A重合),过点D作交的延长线于点F,以,为邻边作矩形,交于点H,连接,则下列结论:①;②当点恰好落在的延长线上时,;③当点在边上运动时,为定值;④当点在边上运动时,长度的最大值为.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,在 ABC中,,点在边上,满足,若,则图中等于的角有 个.
10.如图,在矩形中,,,点是边上一点,,连接,将沿翻折,得到,延长,交的延长线于点,则 .
11.如图,在正方形中,点分别在边上.连接,若,则的正切值为 .
12.如图,已知是平行四边形的边上一点,将沿直线折叠,点落在平行四边形内的点处,且,如果,,的正弦值为,那么的长为 .
13.如图为我国汉代数学家赵爽在注解《周髀算经》时给出的图形,人们称它为“赵爽弦图”.图形是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是120,小正方形面积是20,则 .
14.七巧板是我国一款传统的益智玩具,能够启迪智慧,陶冶情操.七巧板是由五块含45°角的直角三角形、一块正方形和一块平行四边形组成的.某同学利用图1中七巧板的部分图形拼成图2中的图形.若,则的值为 .
三、解答题
15.计算:.
16.计算:
17.如图,已知 ABC中,于点D,,连接并延长交边于点F,已知,
(1)求的正切值;
(2)求的值.
18.如图,是的直径,点为上一点,过点作的垂线,交过点的切线于点,交于点,连接交于点.
(1)求证:.
(2)若的半径为10,,求的长.
19.如图,是的外接圆,为直径,点是劣弧ED的中点,连接,,过点作交的延长线于点,使得.
(1)求证:为的切线;
(2)求证:;
(3)若的半径,,求的长度.
20.在如图的直角三角形中,我们知道,,,
∴.即一个角的正弦和余弦的平方和为1.
(1)请你根据上面的探索过程,探究,与之间的关系;
(2)请你利用上面探究的结论解答下面问题:已知为锐角,且,求的值.
21.如图,在菱形中,为锐角,是对角线上的一个动点,连接.
(1)如图,求证:;
(2)如图,在左侧作,延长分别交于点.
①当,时,求的长;
②如图,在上截取,连接交于点,连接交对角线于点,求证:四边形是平行四边形.
22.在中,,是上一点,,点在上.
(1)过点作的垂线分别交,于,.
①如图1,当时,________,________;
②如图2,若是的中点,当时,求证: ADE是等边三角形;
(2)如图3,若是的中点,,直接写出的值.
23.已知a、b、c分别是 ABC的角A、B、C的对边(),二次函数图像的顶点在x轴上,且、是关于x的方程的两个根.
(1)判断 ABC的形状;
(2)求m的值;
(3)若这个三角形的外接圆面积为,求 ABC的内接正方形的边长.
24.阅读理解:
如图①,在中,,根据锐角三角函数的定义,我们可以得出以下结论:.
(1)如图②,在矩形中,,连接,若,求的长;
(2)如图③,李叔叔有一块形状为菱形的地,其中,李叔叔想在地中间开辟一块矩形区域种植花卉,花卉四周种植树木,每棵树木相隔2m,他在上取了一点E,过点E作交于点H,过点H作交于点G,过点G作交于点F,连接,则矩形就是他想要种植花卉和树木的区域.
①在种植过程中,他发现需要种植树木的数量(单位:棵)随着长度(单位:m)的变化而变化,请完成下表:
长度/m 10 20 30 …
需要种植树木的数量/棵 …
若用y表示需要种植树木的数量,x表示AE的长度,试求出y与x的关系式;
②当矩形是正方形时,求正方形的一条边上最多可以种植多少棵树
试卷第1页,共3页
试卷第1页,共3页
《九年级数学下册人教版第二十八章第1节《锐角三角函数》课时练习》参考答案
题号 1 2 3 4 5 6 7 8
答案 D A B B D C C D
9.2
10.
11.
12.
13.
14.
15.解:原式
.
16.解:
17.(1)解:∵,
∴,
在中,,
∴,
由勾股定理得:,
∵,
∴,
∴,
∴;
(2)解:∵,
∴,
过D作交于点G,
∴,,
∴,
设,则,
∴.
18.(1)证明:∵是的切线,
∴,
∴.
∵,
∴,
∴.
∵,
∴.
(2)解:连接,如图所示,
∵是的直径,的半径为10,
∴,.
∵在中,,
∴,
∴.
∵,
∴,
∴,
∴.
∵,,
∴,
∴.
设,则.
∵在中,,
∴,
∴(负值已舍去),
∴
19.(1)证明:连接,
,
,
,
为直径,
,
,
,
,
,
过半径的外端点,且,
为的切线;
(2)证明:为劣弧的中点,
,
∵,,
,
;
(3)解:过点作于点,
∵,,
∴,
∴,
∴,
∴,
∵为直径,
∴,
∴,
,
在中,,,
,
∴,
,,,
,
∴,
∴,
,
,,
,,
,
,
,
.
20.(1)解:∵,,,
∴,
∴.
(2)解:∵,且,
∴.
21.(1)证明:∵四边形是菱形,
∴,,
又∵,
∴;
(2)解:①∵,
∴,
∵,
∴,
∵四边形是菱形,
∴,
∴,
∴,
∴,
过点作于,则,,
∵,
∴,
∴,
即,
∴,
∴;
②延长至,
∵四边形是菱形,
∴,,,
∵,
∴,,
又∵,
∴,
∴,
∴,
即,
在和中,
,
∴,
∴,
在和 ADE中,
,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
即,
∵,
∴四边形是平行四边形.
22.(1)①作于,则.
由题意知:n=2,设CD=1,
∴BD=2.
在△ABC,△DCP,△ADP中
∵BD=2,CD=1,AB=AC,∠BAC=
∴AB=AC= ,DP=CP=,
∴AP=,
在△AEM和△AFM中,
∵AD⊥EF,∠BAC=
∴
∴△MAF∽△MEA
∴,∠AEM=∠FAM
又∵∠DAP=∠FAM,∠FAM=∠AEM
∴
故答案为,.
②作于,则,
,
,
,
,
,
,.
又,是的中点,
,
因为 ADE是等边三角形.
(2)作AO⊥BC,MN⊥BC分别交BC与点O,N.
由题意知:
∴∠MCB=
设AO=2.
∵点M为AD的中点,AB=AC,AO⊥BC
∴MN=AO=1,ON=ND,BO=OC=2
在△MNC中
∵∠MCB=,MN⊥BC,MN=1
∴MC=2,NC=
∴ON=OC-NC=
∵ON=ND,ON=
∴ND=,OD=
即BD=,CD=.
∴.
23.(1) ABC是直角三角形;
证明:将化简得到,
由于二次函数图像的顶点在x轴上,
,
;
故 ABC是直角三角形;
(2)解: ABC是直角三角形,,
,
,
、是关于x的方程的两个根,
,
,
,
,
整理得,
解得,
经检验,都是原方程的根,
当时,,
当时,舍去,
故;
(3)解:由于三角形的外接圆面积为,
外接圆半径,
斜边,
将代入方程得到,
解得,
,
设正方形边长为,
由,
得,
解得;
图2中,,
,
即,
解得.
综上所述, ABC的内接正方形的边长为或.
24.(1)∵角B是90度,∴,
解得.
在中,;
(2)①表格种依次填写:156,152,148;
如图,连接交于点O,交于点M,设交于点N.
∵四边形是菱形,
∴,
∴.
由菱形的对称性可知,,
∵时,.
∵,,
∴,.
∵每棵树木相隔2m,,,
所以当时,需要种植树木得数量是(棵);
同理:当时,需要种植树木得数量是152棵;
当时,需要种植树木得数量是148棵.
故答案为:156,152,148;
如图,连接交于点O,交于点M,设交于点N.
∵四边形是菱形,
∴,
∴.
由菱形的对称性可知,,
当时,,
∵,,
∴,.
∵每棵树木相隔2m,,,
∴;
②当矩形是正方形时,由题意可得,
,
解得,
此时,
∴,
∴正方形得一条边上最多可以种植35棵树.
答案第1页,共2页
答案第1页,共2页
