4.1.2 相交直线所成的角 教案
图片预览

文档简介
中小学教育资源及组卷应用平台
4.1.2 相交直线所成的角
——新授课
一、教材分析
《4.1.2 相交直线所成的角》是湘教版七年级下册第四章第一节第二课时的内容,相交直线所成的角是在学生已经学习了直线、射线、线段和角的基础上进行的,它是进一步研究平行线的性质和判定的基础,在平面几何中起着承上启下的重要作用。通过对相交直线所成角的学习,学生能够更好地理解几何图形的性质和关系,为后续学习三角形、四边形等几何图形奠定坚实的基础。
二、学情分析
七年级学生正处于从形象思维向抽象思维过渡的关键时期。在小学阶段,他们已对一些简单的几何图形有了初步了解,具备一定的直观感知能力。但对于较为抽象的几何概念和逻辑推理,理解起来仍有一定难度。在本单元学习过程中,学生对直观形象的生活实例和动手操作活动兴趣浓厚,因此在教学中应充分利用这一特点,通过大量实例展示、动手探究活动等方式,引导学生逐步从直观感知上升到理性思考,帮助他们更好地理解和掌握抽象的几何知识,培养其逻辑推理能力和空间观念。
三、教学目标
1.理解相交直线所成的角的意义,理解对顶角、同位角、内错角、同旁内角的概念。
2.掌握对顶角的性质,能运用对顶角的性质求角的度数。
3.能够在复杂的图形中准确找出同位角、内错角和同旁内角。
四、重点难点
重点:理解对顶角、同位角、内错角、同旁内角的概念,掌握对顶角的性质。
难点:在复杂图形中准确找出同位角、内错角和同旁内角。
五、教学方法
讲授法、练习法、问答法
六、教学过程
一、复习回顾
【回顾】
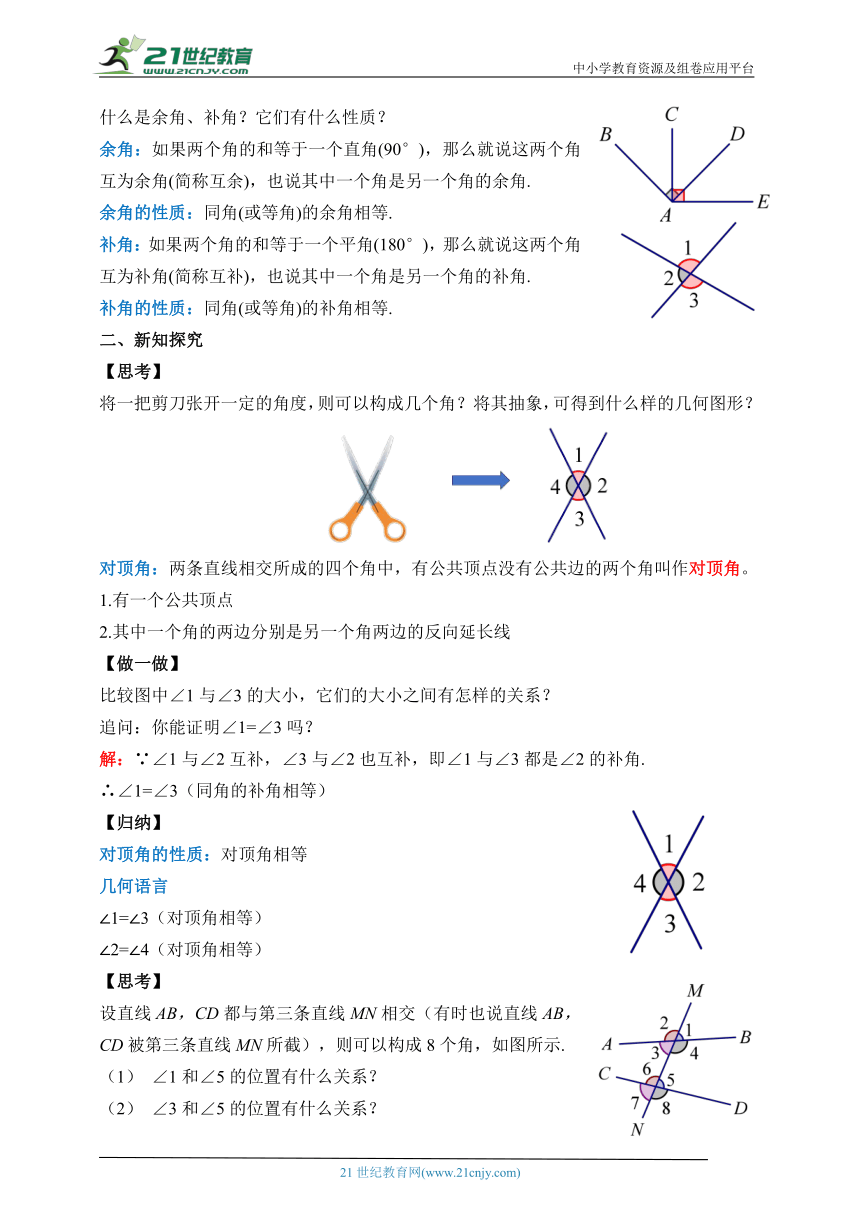
什么是余角、补角?它们有什么性质?
余角:如果两个角的和等于一个直角(90°),那么就说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
余角的性质:同角(或等角)的余角相等.
补角:如果两个角的和等于一个平角(180°),那么就说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
补角的性质:同角(或等角)的补角相等.
二、新知探究
【思考】
将一把剪刀张开一定的角度,则可以构成几个角?将其抽象,可得到什么样的几何图形?
对顶角:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角。
1.有一个公共顶点
2.其中一个角的两边分别是另一个角两边的反向延长线
【做一做】
比较图中∠1与∠3的大小,它们的大小之间有怎样的关系?
追问:你能证明∠1=∠3吗?
解:∵∠1与∠2互补,∠3与∠2也互补,即∠1与∠3都是∠2的补角.
∴∠1=∠3(同角的补角相等)
【归纳】
对顶角的性质:对顶角相等
几何语言
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
【思考】
设直线AB,CD都与第三条直线MN相交(有时也说直线AB,CD被第三条直线MN所截),则可以构成8个角,如图所示.
(1) ∠1和∠5的位置有什么关系?
(2) ∠3和∠5的位置有什么关系?
(3) ∠3和∠6的位置有什么关系?
讲授:
∠1和∠5分别在直线AB,CD的同一方(上方),并且都在直线MN的同侧(右侧).
具有∠1和∠5这种位置关系的一对角叫作同位角.
特点:同方、同侧
∠3和∠5都在直线AB,CD之间,并且分别在直线MN的两侧(∠3在直线MN左侧,∠5在直线MN右侧).
具有∠3和∠5这种位置关系的一对角叫作内错角.
特点:两侧、两线之间
∠3和∠6都在直线AB,CD之间,但它们在直线MN的同一旁(左侧).
具有∠3和∠6这种位置关系的一对角叫作同旁内角.
特点:同侧、两线之间
【思考】
你还能找到其它同位角、内错角、同旁内角吗?
同位角 :∠4与∠8、∠2与∠6、∠3与∠7
内错角 :∠4与∠6
同旁内角:∠4与∠5
三、例题探究
例1直线EF与直线AB,CD分别相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角:∠1与∠3、∠2与∠4、∠5与∠7、∠6与∠8
同位角:∠1与∠8、∠2与∠5、∠3与∠6、 ∠4与∠7
内错角:∠1与∠6、∠4与∠5
同旁内角:∠1与∠5、∠4与∠6
例2如图,直线AB,CD被直线MN所截,同位角∠1与∠2相等,那么内错角∠2与∠3相等吗?
解:∵∠1=∠3(对顶角相等),
∠1=∠2(已知),
∴∠2=∠3(等量代换).
归纳
两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
四、课堂小结
对顶角:
1.有一个公共顶点
2.两边的互为反向延长线
对顶角的性质:对顶角相等
同位角:同方、同侧
内错角:两侧、两线之间
同旁内角:同侧、两线之间
五、课堂练习
1.下列图形中,∠1与∠2是对顶角的是 ( )
A. B. C. D.
2. 下列说法中错误的是 ( )
A. 同一个角的两个邻补角是对顶角
B. 对顶角相等,相等的角是对顶角
C. 对顶角的平分线在一条直线上
D. 不相等的角一定不是对顶角
3.如图所示.
(1)∠AED和∠ABC可看成是直线 、 被直线 所截得的 角.
(2)∠EDB和∠DBC可看成是直线 、 被直线 所截得的 角.
(3)∠EDC和∠C可看成是直线 、 被直线 所截得的 角.
六、作业布置
课堂作业:P95 T3
家庭作业:《学法》P57——58 A组(基础一般)、B组(基础较好)、C组(选做)
七、教学反思
在本节课的教学过程中,要充分关注学生的学习情况,及时调整教学方法和进度。对于学生在识别同位角、内错角和同旁内角时容易出现的错误,要进行针对性的指导和强化训练。通过多样化的教学方法,激发学生的学习兴趣,提高课堂教学效果。同时,在教学中要注重培养学生的数学思维能力和空间观念,为学生后续学习几何知识奠定良好的基础。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
4.1.2 相交直线所成的角
——新授课
一、教材分析
《4.1.2 相交直线所成的角》是湘教版七年级下册第四章第一节第二课时的内容,相交直线所成的角是在学生已经学习了直线、射线、线段和角的基础上进行的,它是进一步研究平行线的性质和判定的基础,在平面几何中起着承上启下的重要作用。通过对相交直线所成角的学习,学生能够更好地理解几何图形的性质和关系,为后续学习三角形、四边形等几何图形奠定坚实的基础。
二、学情分析
七年级学生正处于从形象思维向抽象思维过渡的关键时期。在小学阶段,他们已对一些简单的几何图形有了初步了解,具备一定的直观感知能力。但对于较为抽象的几何概念和逻辑推理,理解起来仍有一定难度。在本单元学习过程中,学生对直观形象的生活实例和动手操作活动兴趣浓厚,因此在教学中应充分利用这一特点,通过大量实例展示、动手探究活动等方式,引导学生逐步从直观感知上升到理性思考,帮助他们更好地理解和掌握抽象的几何知识,培养其逻辑推理能力和空间观念。
三、教学目标
1.理解相交直线所成的角的意义,理解对顶角、同位角、内错角、同旁内角的概念。
2.掌握对顶角的性质,能运用对顶角的性质求角的度数。
3.能够在复杂的图形中准确找出同位角、内错角和同旁内角。
四、重点难点
重点:理解对顶角、同位角、内错角、同旁内角的概念,掌握对顶角的性质。
难点:在复杂图形中准确找出同位角、内错角和同旁内角。
五、教学方法
讲授法、练习法、问答法
六、教学过程
一、复习回顾
【回顾】
什么是余角、补角?它们有什么性质?
余角:如果两个角的和等于一个直角(90°),那么就说这两个角互为余角(简称互余),也说其中一个角是另一个角的余角.
余角的性质:同角(或等角)的余角相等.
补角:如果两个角的和等于一个平角(180°),那么就说这两个角互为补角(简称互补),也说其中一个角是另一个角的补角.
补角的性质:同角(或等角)的补角相等.
二、新知探究
【思考】
将一把剪刀张开一定的角度,则可以构成几个角?将其抽象,可得到什么样的几何图形?
对顶角:两条直线相交所成的四个角中,有公共顶点没有公共边的两个角叫作对顶角。
1.有一个公共顶点
2.其中一个角的两边分别是另一个角两边的反向延长线
【做一做】
比较图中∠1与∠3的大小,它们的大小之间有怎样的关系?
追问:你能证明∠1=∠3吗?
解:∵∠1与∠2互补,∠3与∠2也互补,即∠1与∠3都是∠2的补角.
∴∠1=∠3(同角的补角相等)
【归纳】
对顶角的性质:对顶角相等
几何语言
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
【思考】
设直线AB,CD都与第三条直线MN相交(有时也说直线AB,CD被第三条直线MN所截),则可以构成8个角,如图所示.
(1) ∠1和∠5的位置有什么关系?
(2) ∠3和∠5的位置有什么关系?
(3) ∠3和∠6的位置有什么关系?
讲授:
∠1和∠5分别在直线AB,CD的同一方(上方),并且都在直线MN的同侧(右侧).
具有∠1和∠5这种位置关系的一对角叫作同位角.
特点:同方、同侧
∠3和∠5都在直线AB,CD之间,并且分别在直线MN的两侧(∠3在直线MN左侧,∠5在直线MN右侧).
具有∠3和∠5这种位置关系的一对角叫作内错角.
特点:两侧、两线之间
∠3和∠6都在直线AB,CD之间,但它们在直线MN的同一旁(左侧).
具有∠3和∠6这种位置关系的一对角叫作同旁内角.
特点:同侧、两线之间
【思考】
你还能找到其它同位角、内错角、同旁内角吗?
同位角 :∠4与∠8、∠2与∠6、∠3与∠7
内错角 :∠4与∠6
同旁内角:∠4与∠5
三、例题探究
例1直线EF与直线AB,CD分别相交,构成8个角.指出图中所有的对顶角、同位角、内错角和同旁内角.
解:对顶角:∠1与∠3、∠2与∠4、∠5与∠7、∠6与∠8
同位角:∠1与∠8、∠2与∠5、∠3与∠6、 ∠4与∠7
内错角:∠1与∠6、∠4与∠5
同旁内角:∠1与∠5、∠4与∠6
例2如图,直线AB,CD被直线MN所截,同位角∠1与∠2相等,那么内错角∠2与∠3相等吗?
解:∵∠1=∠3(对顶角相等),
∠1=∠2(已知),
∴∠2=∠3(等量代换).
归纳
两条直线被第三条直线所截,如果有一对同位角相等,则内错角相等.
四、课堂小结
对顶角:
1.有一个公共顶点
2.两边的互为反向延长线
对顶角的性质:对顶角相等
同位角:同方、同侧
内错角:两侧、两线之间
同旁内角:同侧、两线之间
五、课堂练习
1.下列图形中,∠1与∠2是对顶角的是 ( )
A. B. C. D.
2. 下列说法中错误的是 ( )
A. 同一个角的两个邻补角是对顶角
B. 对顶角相等,相等的角是对顶角
C. 对顶角的平分线在一条直线上
D. 不相等的角一定不是对顶角
3.如图所示.
(1)∠AED和∠ABC可看成是直线 、 被直线 所截得的 角.
(2)∠EDB和∠DBC可看成是直线 、 被直线 所截得的 角.
(3)∠EDC和∠C可看成是直线 、 被直线 所截得的 角.
六、作业布置
课堂作业:P95 T3
家庭作业:《学法》P57——58 A组(基础一般)、B组(基础较好)、C组(选做)
七、教学反思
在本节课的教学过程中,要充分关注学生的学习情况,及时调整教学方法和进度。对于学生在识别同位角、内错角和同旁内角时容易出现的错误,要进行针对性的指导和强化训练。通过多样化的教学方法,激发学生的学习兴趣,提高课堂教学效果。同时,在教学中要注重培养学生的数学思维能力和空间观念,为学生后续学习几何知识奠定良好的基础。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
