8.3动能和动能定理 课件(共35张PPT)-2024-2025学年高中《物理》(人教版2019)必修2
文档属性
| 名称 | 8.3动能和动能定理 课件(共35张PPT)-2024-2025学年高中《物理》(人教版2019)必修2 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-17 07:29:29 | ||
图片预览









文档简介
(共35张PPT)
动能和动能定理
高一年级 物理
W
Ek
W为合力做的总功(过程量)
若合力做正功,即W>0,则Ek2>Ek1 ,动能增大
若合力做负功,即W<0,则Ek2<Ek1 ,动能减小
Ek1和Ek2分别为初、末状态的动能(状态量)
△Ek =Ek2-Ek1为动能的变化(过程量)
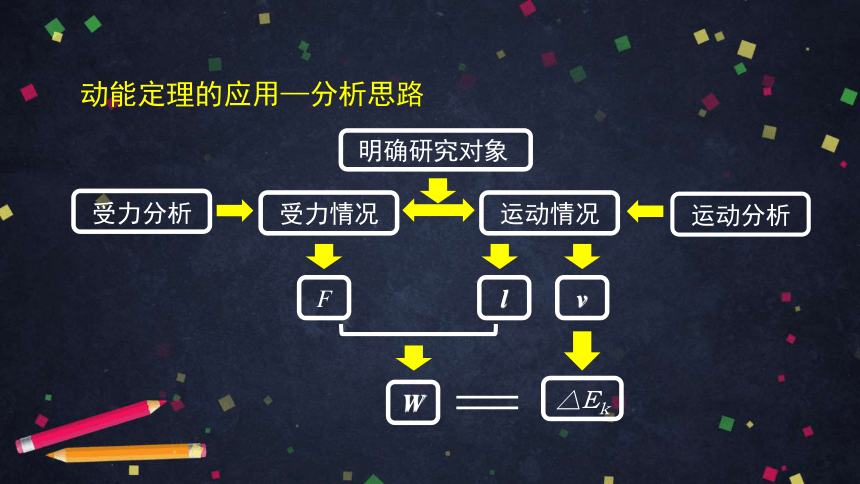
受力分析
运动情况
受力情况
运动分析
F
l
v
明确研究对象
W
△Ek
动能定理的应用—分析思路
既适用于直线运动,也适用于曲线运动。
既适用于恒力做功,也适用于变力做功。
既适用于一个过程,也适用于整个过程。
动能定理的适用范围
一、多个运动过程的问题
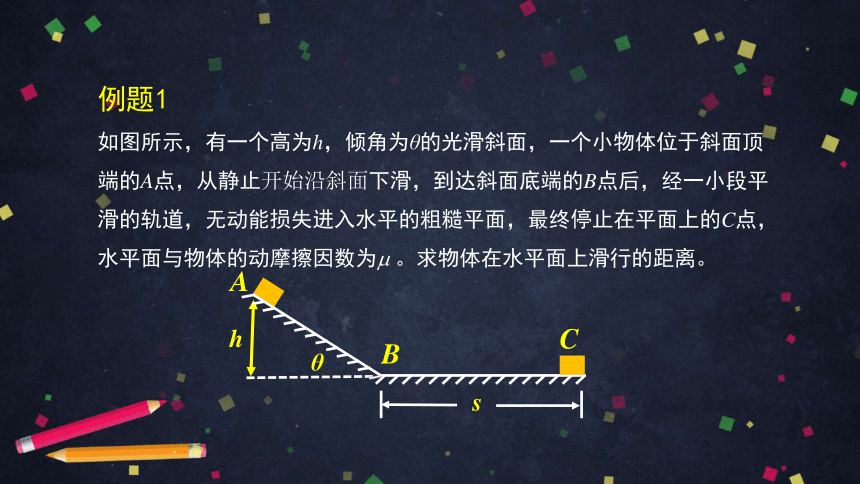
例题1
如图所示,有一个高为h,倾角为θ的光滑斜面,一个小物体位于斜面顶端的A点,从静止开始沿斜面下滑,到达斜面底端的B点后,经一小段平滑的轨道,无动能损失进入水平的粗糙平面,最终停止在平面上的C点,水平面与物体的动摩擦因数为 。求物体在水平面上滑行的距离。
B
C
s
A
h
θ
分析与解答:
这是一个多过程问题,包含两个匀变速直线运动,可以用牛顿运动定律求解,也可以用动能定理来求解。
对比用牛顿运动定律和动能定理两种求解方法,我们能更好地理解使用动能定理求解的便捷之处。
受力分析:
N1
mg
θ
运动分析:
做功分析:
动能分析:
匀变速直线运动,初速度为0,末速度为vB
位移为 h/sinθ
重力做功WG = mgh,支持力不做功
初动能为零,末动能为
F合 = mgsinθ
从A滑动到B的过程
解法一:使用牛顿运动定律
解法二:使用动能定理
N1
mg
θ
解得:
解得:
从A滑动到B的过程
受力分析:
运动分析:
做功分析:
动能分析:
匀变速直线运动,初速度为vB ,末速度为0
位移为S
摩擦力做功Wf = - μmgS
F合 = f = μmg
初动能为 ,末动能为0
f
N2
mg
从B滑动到C的过程
从B滑动到C的过程
f
N2
mg
代入
得
代入
得
解法一:使用牛顿运动定律
解法二:使用动能定理
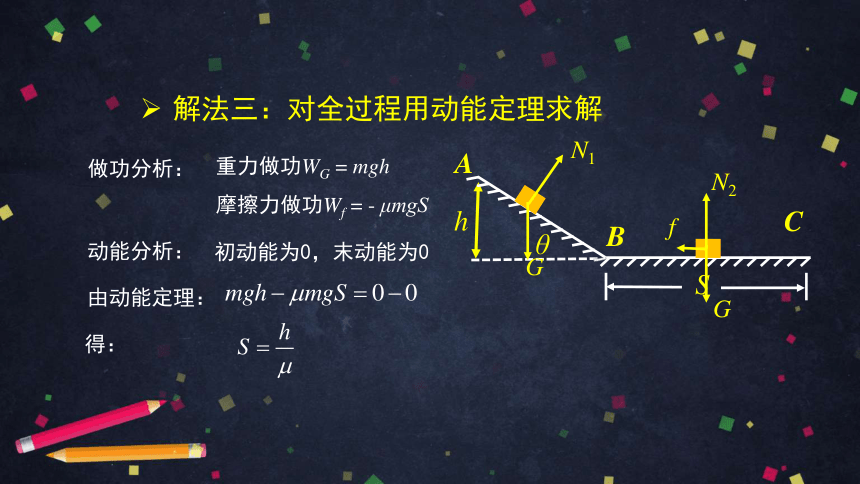
解法三:对全过程用动能定理求解
得:
B
C
S
A
h
θ
N1
G
f
N2
G
做功分析:
动能分析:
重力做功WG = mgh
摩擦力做功Wf = - μmgS
初动能为0,末动能为0
由动能定理:
对比牛顿运动定律和动能定理
对于匀变速直线运动的问题,既可以使用牛顿运动定律,也可以用动能定理求解,但是用动能定理一般会更快捷。
对于多过程的问题,动能定理可以对整个过程列式求解,能大大简化计算过程。
如图所示,质量为m的小球从离地h高处由静止释放,小球在运动过程中所受空气阻力是它重力的k倍( k<1),小球每次与地面相碰后,都以与碰前大小相同的速度反弹。求:小球下落直至弹跳停止过程中运动的总路程S。
m
h
例题2
m
h
对小球的受力和运动过程进行分析。
下落过程:F合=(1-k)mg,从静止开始匀加速运动;
反弹过程:速度反向,大小不变;
上升过程: F合=(1+k)mg,匀减速上升到最高点。
之后小球重复上述过程,但是由于阻力的作用,小球每次弹起的高度会比上一次小。经过许多次反弹之后,弹起高度接近于零。这是一个无穷多过程的问题,用牛顿运动定律求解会非常复杂。
分析与解答:
对小球从下落到停止的全过程分析:
重力做功:
阻力做功:对于大小不变的阻力,克服阻力所做的功为阻力的大小乘以物体运动路程:
动能分析:初动能为0,末动能为0
对全过程,由动能定理:
得
二、变力做功的问题
质量为m=1kg的物体被人由静止向上提高h=1m,这时物体的速度是v=2m/s,g取10m/s2,求:
(1)物体克服重力做的功。
(2)合力对物体做的功。
(3)人对物体做的功。
v
m
m
h
A
B
例题3
注意:不要想当然地认为人施加给物体的力是恒力。
该题要求解合力和人施加的力做的功,但没有给出这个力的大小,运动过程也不确定是一个匀变速直线运动,因此不能用牛顿运动定律来求解。
题目给出了物体的质量和运动的初、末速度,可以用动能定理来求解。
分析与解答:
画出物体的运动过程并受力分析:
(1) m由A到B:
克服重力做功
(2) m由A到B,根据动能定理,合力的功为:
(3) 人做的功为:
v
m
m
h
A
B
F
mg
将一个质量为m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从最低点P点缓慢地移动到Q点,如图所示,则力F所做的功为( )
A.mgLcosθ
B.mgL(1-cosθ)
C.FLsinθ
D.FLtanθ
O
L
P
Q
F
θ
例题4
该题很容易错选选项C。
错误的解答过程:
作用力F水平向右;
物体沿水平方向移动的距离为Lsinθ
所以做功为W=FLsinθ
错解原因:W=FS只能用于计算恒力的功,但根据该题的条件可以分析得出F是变化的力。
O
L
P
Q
F
θ
分析与解答:
缓慢移动小球,可以认为小球一直处于速度为零且受力平衡的状态。由三力平衡的条件,可以求出拉力F=mgtanθ,F的大小随角度θ变化,是一个变力,F做的功是变力做功问题,应该用动能定理求解。
重力对小球做功为WG= -mg L(1-cosθ) ,绳子拉力T不做功,小球的动能可以视为零。由动能定理:
-mg L(1-cosθ) + WF =0 - 0
可得: WF=mgL (1-cosθ)
选项B正确。
O
L
P
Q
F
θ
mg
T
正确的解答过程:
某汽车的发动机额定功率为P=60 kW,质量为m=5×103 kg,在水平路面上行驶时,阻力f是重力的0.05倍。若汽车保持额定功率从静止启动, g取10m/s2,求:
v
t
vm
t
O
(1)汽车所能达到的最大速度vm是多大?
(2)如果汽车由启动到速度变为最大值时的位移为S=624 m,求汽车启动过程所用的时间t。
例题5
(1) 当牵引力大小与阻力f大小相同时,物体速度v达到最大值vm。
则: P额 = Fv = fvm
可得: vm= P额/f = 24 m/s.
分析与解答:
恒定功率启动:P=Fv ,速度v增大,牵引力F变小,是一个变力。
(2) 这一问比较难,有几个需要掌握的关键点:
本题中汽车做非匀变速直线运动,不能用之前所学的运动学公式求时间t。
汽车的功率恒定,可以使用W=Pt求发动机的功,从而引入时间t。
汽车的牵引力变化,不能使用W=FS求发动机做的功。
阻力恒定,可以用Wf = - fS求阻力的功。
设由启动到速度达到最大值vm所用的时间为t,对全过程使用动能定理:
代入数据,解得:t=50 s。
三、曲线运动的问题
质量为m的物体从高度h的位置以初速度v0做平抛运动。求落地时速度的大小v。
v
v0
m
h
例题6
解法一:运动合成分解。
分析与解答:
v
v0
m
h
vx
vy
水平方向:
竖直方向:
速度合成:
解法二:动能定理。
得:
物体从抛出到落地的过程,只有重力做功WG=mgh。由动能定理:
注意:该结果与物体抛出的初速度方向无关。
如图所示,竖直平面内的光滑轨道由一段斜的直轨道AB和与之相切的圆弧形轨道BC连接而成,圆弧形轨道的半径为R。一质量为m的小物块从直轨道上高度为h的地方由静止开始下滑,然后沿圆弧形
轨道运动。求:
m
R
h
A
B
C
(1) 如果h足够高,物块通过圆轨道最高点C时速度为多大?
(2) 要使物体能够达到最高点C,h至少需要多高?
例题7
(1) 对运动全过程,只有重力做功。由动能定理:
分析与解答:
这是一个多过程问题,而且既有直线运动,也有曲线运动,可以对全过程使用动能定理来求解。
得:
m
R
h
A
B
C
(2) 物体恰好能到达C点时,在C点受到的轨道的支持力N=0,由牛顿第二定律:
由动能定理:
得:
得:
mg
R
vC
课堂小结
多过程问题
变力做功问题
曲线运动问题
受力分析
运动分析
做功分析
动能分析
动能和动能定理
高一年级 物理
W
Ek
W为合力做的总功(过程量)
若合力做正功,即W>0,则Ek2>Ek1 ,动能增大
若合力做负功,即W<0,则Ek2<Ek1 ,动能减小
Ek1和Ek2分别为初、末状态的动能(状态量)
△Ek =Ek2-Ek1为动能的变化(过程量)
受力分析
运动情况
受力情况
运动分析
F
l
v
明确研究对象
W
△Ek
动能定理的应用—分析思路
既适用于直线运动,也适用于曲线运动。
既适用于恒力做功,也适用于变力做功。
既适用于一个过程,也适用于整个过程。
动能定理的适用范围
一、多个运动过程的问题
例题1
如图所示,有一个高为h,倾角为θ的光滑斜面,一个小物体位于斜面顶端的A点,从静止开始沿斜面下滑,到达斜面底端的B点后,经一小段平滑的轨道,无动能损失进入水平的粗糙平面,最终停止在平面上的C点,水平面与物体的动摩擦因数为 。求物体在水平面上滑行的距离。
B
C
s
A
h
θ
分析与解答:
这是一个多过程问题,包含两个匀变速直线运动,可以用牛顿运动定律求解,也可以用动能定理来求解。
对比用牛顿运动定律和动能定理两种求解方法,我们能更好地理解使用动能定理求解的便捷之处。
受力分析:
N1
mg
θ
运动分析:
做功分析:
动能分析:
匀变速直线运动,初速度为0,末速度为vB
位移为 h/sinθ
重力做功WG = mgh,支持力不做功
初动能为零,末动能为
F合 = mgsinθ
从A滑动到B的过程
解法一:使用牛顿运动定律
解法二:使用动能定理
N1
mg
θ
解得:
解得:
从A滑动到B的过程
受力分析:
运动分析:
做功分析:
动能分析:
匀变速直线运动,初速度为vB ,末速度为0
位移为S
摩擦力做功Wf = - μmgS
F合 = f = μmg
初动能为 ,末动能为0
f
N2
mg
从B滑动到C的过程
从B滑动到C的过程
f
N2
mg
代入
得
代入
得
解法一:使用牛顿运动定律
解法二:使用动能定理
解法三:对全过程用动能定理求解
得:
B
C
S
A
h
θ
N1
G
f
N2
G
做功分析:
动能分析:
重力做功WG = mgh
摩擦力做功Wf = - μmgS
初动能为0,末动能为0
由动能定理:
对比牛顿运动定律和动能定理
对于匀变速直线运动的问题,既可以使用牛顿运动定律,也可以用动能定理求解,但是用动能定理一般会更快捷。
对于多过程的问题,动能定理可以对整个过程列式求解,能大大简化计算过程。
如图所示,质量为m的小球从离地h高处由静止释放,小球在运动过程中所受空气阻力是它重力的k倍( k<1),小球每次与地面相碰后,都以与碰前大小相同的速度反弹。求:小球下落直至弹跳停止过程中运动的总路程S。
m
h
例题2
m
h
对小球的受力和运动过程进行分析。
下落过程:F合=(1-k)mg,从静止开始匀加速运动;
反弹过程:速度反向,大小不变;
上升过程: F合=(1+k)mg,匀减速上升到最高点。
之后小球重复上述过程,但是由于阻力的作用,小球每次弹起的高度会比上一次小。经过许多次反弹之后,弹起高度接近于零。这是一个无穷多过程的问题,用牛顿运动定律求解会非常复杂。
分析与解答:
对小球从下落到停止的全过程分析:
重力做功:
阻力做功:对于大小不变的阻力,克服阻力所做的功为阻力的大小乘以物体运动路程:
动能分析:初动能为0,末动能为0
对全过程,由动能定理:
得
二、变力做功的问题
质量为m=1kg的物体被人由静止向上提高h=1m,这时物体的速度是v=2m/s,g取10m/s2,求:
(1)物体克服重力做的功。
(2)合力对物体做的功。
(3)人对物体做的功。
v
m
m
h
A
B
例题3
注意:不要想当然地认为人施加给物体的力是恒力。
该题要求解合力和人施加的力做的功,但没有给出这个力的大小,运动过程也不确定是一个匀变速直线运动,因此不能用牛顿运动定律来求解。
题目给出了物体的质量和运动的初、末速度,可以用动能定理来求解。
分析与解答:
画出物体的运动过程并受力分析:
(1) m由A到B:
克服重力做功
(2) m由A到B,根据动能定理,合力的功为:
(3) 人做的功为:
v
m
m
h
A
B
F
mg
将一个质量为m的小球,用长为L的轻绳悬挂于O点。小球在水平拉力F作用下,从最低点P点缓慢地移动到Q点,如图所示,则力F所做的功为( )
A.mgLcosθ
B.mgL(1-cosθ)
C.FLsinθ
D.FLtanθ
O
L
P
Q
F
θ
例题4
该题很容易错选选项C。
错误的解答过程:
作用力F水平向右;
物体沿水平方向移动的距离为Lsinθ
所以做功为W=FLsinθ
错解原因:W=FS只能用于计算恒力的功,但根据该题的条件可以分析得出F是变化的力。
O
L
P
Q
F
θ
分析与解答:
缓慢移动小球,可以认为小球一直处于速度为零且受力平衡的状态。由三力平衡的条件,可以求出拉力F=mgtanθ,F的大小随角度θ变化,是一个变力,F做的功是变力做功问题,应该用动能定理求解。
重力对小球做功为WG= -mg L(1-cosθ) ,绳子拉力T不做功,小球的动能可以视为零。由动能定理:
-mg L(1-cosθ) + WF =0 - 0
可得: WF=mgL (1-cosθ)
选项B正确。
O
L
P
Q
F
θ
mg
T
正确的解答过程:
某汽车的发动机额定功率为P=60 kW,质量为m=5×103 kg,在水平路面上行驶时,阻力f是重力的0.05倍。若汽车保持额定功率从静止启动, g取10m/s2,求:
v
t
vm
t
O
(1)汽车所能达到的最大速度vm是多大?
(2)如果汽车由启动到速度变为最大值时的位移为S=624 m,求汽车启动过程所用的时间t。
例题5
(1) 当牵引力大小与阻力f大小相同时,物体速度v达到最大值vm。
则: P额 = Fv = fvm
可得: vm= P额/f = 24 m/s.
分析与解答:
恒定功率启动:P=Fv ,速度v增大,牵引力F变小,是一个变力。
(2) 这一问比较难,有几个需要掌握的关键点:
本题中汽车做非匀变速直线运动,不能用之前所学的运动学公式求时间t。
汽车的功率恒定,可以使用W=Pt求发动机的功,从而引入时间t。
汽车的牵引力变化,不能使用W=FS求发动机做的功。
阻力恒定,可以用Wf = - fS求阻力的功。
设由启动到速度达到最大值vm所用的时间为t,对全过程使用动能定理:
代入数据,解得:t=50 s。
三、曲线运动的问题
质量为m的物体从高度h的位置以初速度v0做平抛运动。求落地时速度的大小v。
v
v0
m
h
例题6
解法一:运动合成分解。
分析与解答:
v
v0
m
h
vx
vy
水平方向:
竖直方向:
速度合成:
解法二:动能定理。
得:
物体从抛出到落地的过程,只有重力做功WG=mgh。由动能定理:
注意:该结果与物体抛出的初速度方向无关。
如图所示,竖直平面内的光滑轨道由一段斜的直轨道AB和与之相切的圆弧形轨道BC连接而成,圆弧形轨道的半径为R。一质量为m的小物块从直轨道上高度为h的地方由静止开始下滑,然后沿圆弧形
轨道运动。求:
m
R
h
A
B
C
(1) 如果h足够高,物块通过圆轨道最高点C时速度为多大?
(2) 要使物体能够达到最高点C,h至少需要多高?
例题7
(1) 对运动全过程,只有重力做功。由动能定理:
分析与解答:
这是一个多过程问题,而且既有直线运动,也有曲线运动,可以对全过程使用动能定理来求解。
得:
m
R
h
A
B
C
(2) 物体恰好能到达C点时,在C点受到的轨道的支持力N=0,由牛顿第二定律:
由动能定理:
得:
得:
mg
R
vC
课堂小结
多过程问题
变力做功问题
曲线运动问题
受力分析
运动分析
做功分析
动能分析
