2024-2025学年八年级数学下册第一次月考测试卷(考试范围:第16~17章)--人教版(含解析)
文档属性
| 名称 | 2024-2025学年八年级数学下册第一次月考测试卷(考试范围:第16~17章)--人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 985.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 11:20:03 | ||
图片预览



文档简介
2024-2025学年八年级数学下册第一次月考测试卷(考试范围:第16~17章)
一.选择题(共10小题,满分30分,每小题3分)
1.若,化简的结果是( )
A. B.5 C. D.
2.如图,在,,,,以为折痕将翻折,使点与点重合,则的长为( )
A. B.1 C. D.
3.已知,则代数式的值为( )
A. B. C. D.
4.如图,已知为等腰直角三角形,则,,三者的关系为( )
A. B.
C. D.
5.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥4)行从左向右数第(n-3)个数是(用含n的代数式表示)( ).
A. B. C. D.
6.已知m、n是正整数,若+是整数,则满足条件的有序数对(m,n)为( )
A.(2,5) B.(8,20) C.(2,5),(8,20) D.以上都不是
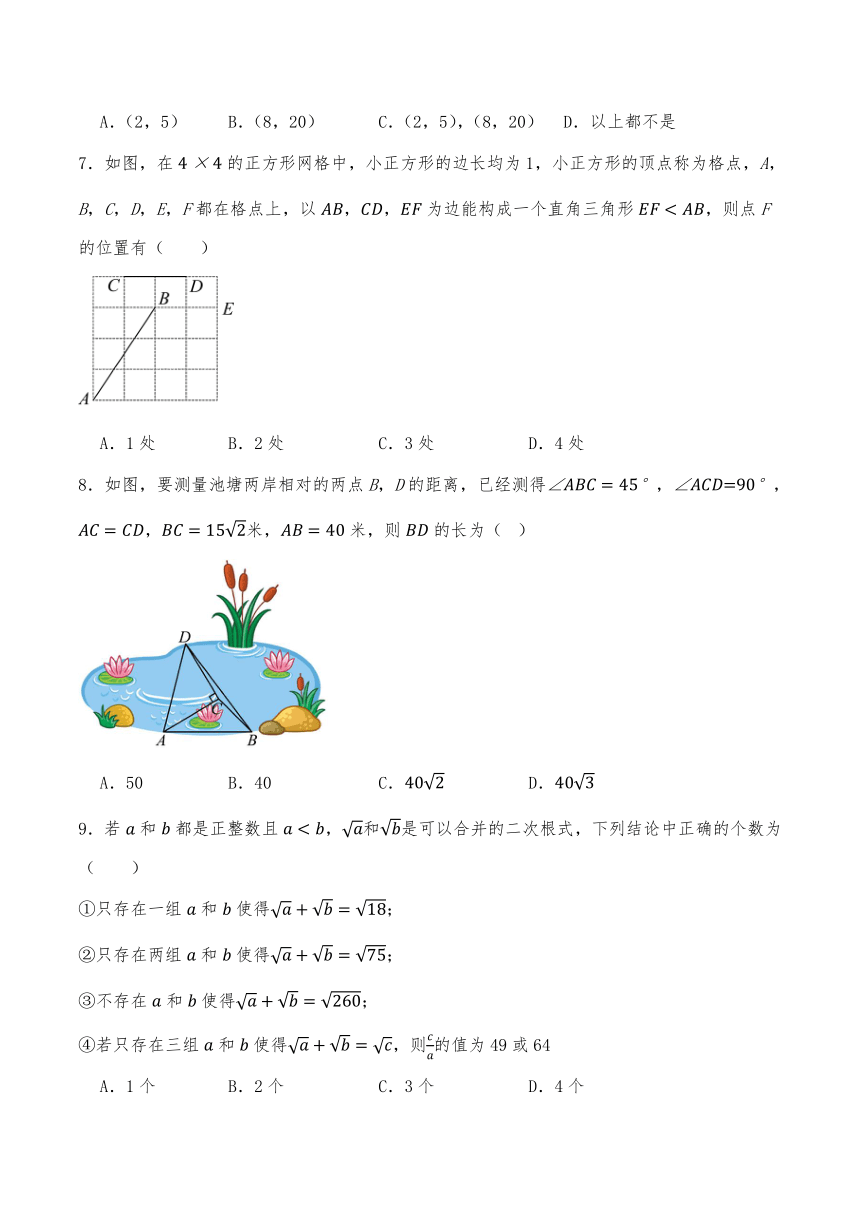
7.如图,在的正方形网格中,小正方形的边长均为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以为边能构成一个直角三角形,则点F的位置有( )
A.1处 B.2处 C.3处 D.4处
8.如图,要测量池塘两岸相对的两点B,D的距离,已经测得,,,米,米,则的长为( )
A.50 B.40 C. D.
9.若和都是正整数且,和是可以合并的二次根式,下列结论中正确的个数为( )
①只存在一组和使得;
②只存在两组和使得;
③不存在和使得;
④若只存在三组和使得,则的值为49或64
A.1个 B.2个 C.3个 D.4个
10.如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9与7,则斜边BC的长为( )
A.5 B.9 C.10 D.16
二.填空题(共6小题,满分18分,每小题3分)
11.已知、满足,则 .
12.如图,有一圆柱形下水管道紧靠墙砖竖直安放,墙砖为长方形,分米,分米,该管道底面是周长为分米的圆,一只蚂蚁从点爬过管道到达,需要走的最短路程是 分米.
13.若,那么的值为 .
14.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P是边AC上一动点,把△ABP沿直线BP折叠,使得点A落在图中点A′处,当△AA′C是直角三角形时,则线段CP的长是 .
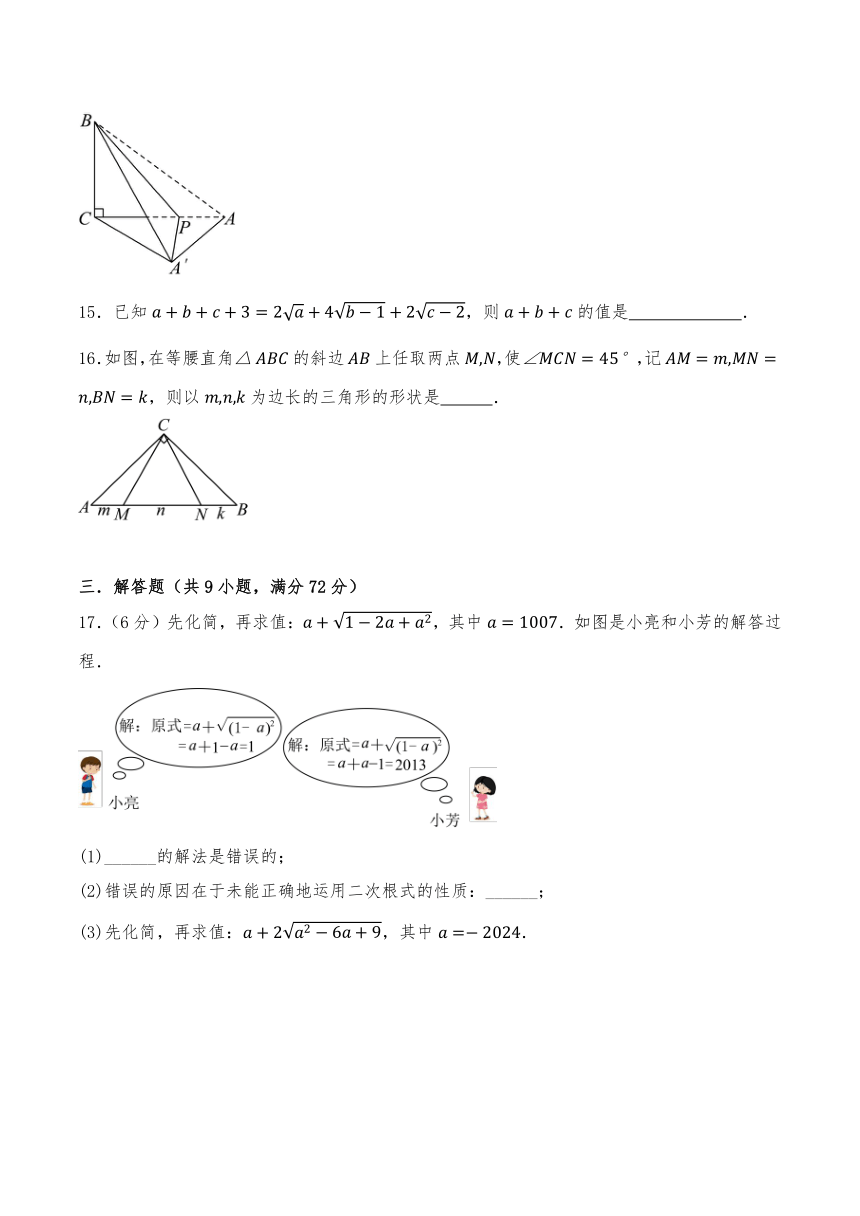
15.已知,则的值是 .
16.如图,在等腰直角的斜边上任取两点,使,记,则以为边长的三角形的形状是 .
三.解答题(共9小题,满分72分)
17.(6分)先化简,再求值:,其中.如图是小亮和小芳的解答过程.
(1)______的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:______;
(3)先化简,再求值:,其中.
18.(6分)先观察下列等式,再回答问题:
①;
②;
③;
(1)根据上面三个等式,请猜想的结果(直接写出结果)
(2)根据上述规律,解答问题:
设,求不超过的最大整数是多少?
19.(6分)平面直角坐标系中,已知点是第一象限角平分线上的点,点,,点,,且.
(1)以下两个结论:①是一个定值;②是一个定值.其中有且只有一个结论正确,请选出来,并求出这个定值.
(2)求四边形的面积.
20.(8分)小明家正在装修,电视背景墙是矩形,其中,,中间要镶一个长为,宽为的矩形大理石图案(图中阴影部分).
(1)矩形的面积是多少?(结果化为最简二次根式)
(2)除去大理石图案部分,其他部分贴壁布,若壁布的造价为8元,大理石的造价为150元,则整个电视墙需要花费多少元?(结果化为最简二次根式)
21.(8分)如图,某小区的两个喷泉A,B位于小路的同侧,两个喷泉间的距离的长为.现要为喷泉铺设供水管道,供水点M在小路上,供水点M到的距离的长为,的长为.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)请求出喷泉B到小路的最短距离.
22.(9分)阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,其实我们还可以将其进一步化简: 以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求.我们可以把ab和ab看成是一个整体,令 xab , y ab ,则.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算: ;
(2)m 是正整数, a ,b 且.求 m.
(3)已知,求的值.
23.(9分)探究一:如图,均为正方形.
问题:()若图中的为直角三角形,的面积为,的面积为,则的面积为________;
()若的面积为,的面积为,同时的面积为,则为________三角形.
探究二:图形变化:
()如图,分别以直角三角形的三边为直径向三角形外作三个半圆,判断这三个半圆的面积之间有什么关系,并说说你的理由;
()如图,如果直角三角形两直角边长分别为和,以直角三角形的三边为直径作半圆,你能利用上面的结论求出阴影部分的面积吗?如果能,请写出你的计算过程;如果不能,请说明理由.
24.(10分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明精彩粉呈,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.
【小试牛刀】(1)把两个全等的直角三角形如图1放置,,已知,,,,试证明.
【知识运用】
(2)如图2,铁路上,两点(看作直线上的两点)相距24千米,,为两个村庄(看作两个点),,,垂足分别为、,千米,千米,则两个村庄的距离为 千米(直接填空);
(3)在(2)的背景下,要在上建造一个供应站,使得,求的长.
(4)【知识迁移】借助上面的思考过程与几何模型,求代数式的最小值 .
25.(10分)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
参考答案
一.选择题
1.B
【分析】本题主要考查了二次根式有意义的条件,二次根式的性质,整式的加减.根据二次根式有意义的条件求得,推出,,据此求解即可.
【详解】解:∵,
∴,,
∴,
∴,,
∴.
故选:B.
2.A
【分析】本题考查的是勾股定理的应用,轴对称的性质,根据勾股定理可以求得,再由勾股定理列出方程即可得出答案.
【详解】解:∵在,,,,
∴,
设,则,
由折叠可知,
在中,,
∴,
∴,
∴.
∴.
故选:A
3.C
【分析】根据已知,得到,整体思想带入求值即可.
【详解】解:∵,
∴,
∴
.
故选C.
4.C
【分析】过点C作,使,连接,,证明,进而得出,,再得出是等腰直角三角形,再根据勾股定理即可得解.
【详解】解:如图,过点C作,使,连接,,
是等腰直角三角形,,
,
,
,
在和中,
,
,,
,
是等腰直角三角形,
,
在中,,
,
故选C.
5.C
【分析】观察数阵排列,可发现各数的被开方数是从1开始的连续自然数,行数中的数字个数是行数的2倍,求出n-1行的数字个数,再加上从左向右的第n-3个数,就得到所求数的被开方数,再写成算术平方根的形式即可.
【详解】由图中规律知,前(n-1)行的数据个数为2+4+6+…+2(n-1)=n(n-1),
∴第n(n是整数,且n≥4)行从左向右数第(n-3)个数的被开方数是:n(n-1)+n-3=n2-3,
∴第n(n是整数,且n≥4)行从左向右数第(n-3)个数是:
故选:C.
【点睛】本题考查了数字规律的知识;解题的关键是熟练掌握数字规律、二次根式的性质,从而完成求解.
6.C
【分析】根据二次根式的性质分析即可得出答案.
【详解】解:∵+是整数,m、n是正整数,
∴m=2,n=5或m=8,n=20,
当m=2,n=5时,原式=2是整数;
当m=8,n=20时,原式=1是整数;
即满足条件的有序数对(m,n)为(2,5)或(8,20),
故选:C.
7.B
【分析】先利用勾股定理求出的长,再根据勾股定理的逆定理,如果满足,则,即为直角三角形,解出的长满足,进而得出点F的位置.
【详解】解:由题意可得,.
∵以为边能构成一个直角三角形,且
∴,
即,
解得,
∴F点的位置如图所示,共2处.
故选:B.
8.A
【分析】本题考查的是勾股定理的应用,二次根式的化简,等腰三角形的判定,作出合适的辅助线是解本题的关键,如图,过作于,过作于,求解,,,,延长交于,则,由勾股定理可得:,可得:,,同理可得:,可得:,,,再进一步求解即可.
【详解】解:如图,过作于,过作于,
∴,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴,
延长交于,则,
由勾股定理可得:,
∴,
解得:,
∴,
∴,
∴,
∴,
同理可得:,
∴,
解得:,
∴,,
∴.
故选:A
9.C
【分析】直接利用同类二次根式的定义得出和是同类二次根式,进而得出答案.
【详解】解:①和都是正整数且,和可以合并的二次根式,
,
,
当时,
故该选项①正确;
②,
当,则
当则.
故选项②正确;
③,
当时,
,所以不存在,
故该选项③正确;
④,
,
当时,,
,
,
有无数和满足等式,故该选项④错误.
故选:C.
10.C
【分析】设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,根据勾股定理得到c2+b2=a2,根据等式的性质得到c2+b2=a2.根据等边三角形的面积公式得到S3=a2,S2=c2,S1=b2,根据已知条件列方程即可得到结论.
【详解】解:如图,设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,
∵△ABC是直角三角形,且∠BAC=90度,
∴c2+b2=a2,
∴c2+b2=a2.
∵S3=a2,S2=c2,S1=b2,
∴S3﹣S2=(a2﹣c2)=b2=9,S3﹣S1=a2﹣b2=(a2﹣b2)=c2=+=,
∴b=6,c=8,
即AB=8,AC=6,
∴BC===10,
故选:C.
二.填空题
11.或34
【分析】本题考查二次根式有意义的条件;根据被开方数大于等于0列式不等式,求出x,再求出y,然后代入代数式进行计算即可得解.
【详解】解:依题意,得:,
解得:;
当时,
;
∴;
当时,
;
∴;
∴的值为或34,
故答案为:或34.
12.
【分析】本题考查了勾股定理的应用最短路线问题,把圆柱侧面展开,由两点之间,线段最短,可知线段为蚂蚁爬行的最短路径,利用勾股定理计算即可求解,正确画出图形是解题的关键.
【详解】解:把圆柱侧面展开,如图,则分米,分米,
由两点之间,线段最短,可知线段为蚂蚁爬行的最短路径,
由勾股定理得,分米,
∴需要走的最短路程是分米,
故答案为:.
13.
【分析】本题考查了二次根式的混合运算、完全平方公式,熟练掌握并灵活运用完全平方公式是解题关键.利用完全平方公式将变形为,再代入的值进行运算求值即可得.
【详解】解: ,
故答案为:.
14.4或3
【分析】分类讨论分别当∠AA′C=90°时,当∠ACA′=90°时,根据折叠的性质函数直角三角形的性质即可得到结论.
【详解】解:如图1,当∠AA′C=90°时,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴AP=A′P,
∴∠PAA′=∠AA′P,
∵∠ACA′+∠PAA′=∠CA′P+∠AA′P=90°,
∴∠PCA′=∠PA′C,
∴PC=PA′,
∴PC=AC=4,
如图2,当∠ACA′=90°时,
∵在Rt△ABC中,∠ACB=90°,且AC=8,BC=6.
∴AB=10,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴A′B=AB=10,PA=PA′,
∴A′C=4,
设PC=x,
∴AP=8-x,
∵A′C2+PC2=PA′2,
∴42+x2=(8-x)2,
解得:x=3,
∴PC=3,
综上所述:当△AA′C是直角三角形时,则线段CP的长是4或3,
故答案为:4或3.
15.9
【分析】先将原等式变形为,再根据平方的非负性可得,,,由此可求得a、b、c的值,进而可求得答案.
【详解】解:∵,
∴,
∴,
∴,,,
∴,,,
∴,,,
∴,
故答案为:9.
16.直角三角形
【分析】本题考查等腰直角三角形的性质,难度较大,注意掌握旋下列情形常实施旋转变换:(1)图形中出现等边三角形或正方形,把旋转角分别定为、;(2)图形中有线段的中点,将图形绕中点旋转,构造中心对称全等三角形;(3)图形中出现有公共端点的线段,将含有相等线段的图形绕公共端点,旋转两相等线段的夹角后与另一相等线段重合.
把绕点逆时针旋转,得,这样就集中成一个与 相等的角,在一条直线上的、、集中为,只需判定的形状即可.
【详解】解:如图:把绕点逆时针旋转,得,
则,
,
又,
∴,
,
又,
,
∴以、、为边长的三角形的形状是直角三角形.
故答案为:直角三角形.
三.解答题
17.(1)解:当时,
原式
原式
,
小亮错误,
故答案:小亮.
(2)解:由题意得
;
故答案:.
(3)解:当时,
原式
原式
.
18.(1)解:① ;
② ;
③ ,
故.
(2)解:①
;
②
;
③
,
,……
,
故.
故不超过的最大整数是2023.
19.(1)结论①正确,理由如下:
点是第一象限角平分线上的点,
,
解得:,
,,
即点P的坐标为,
点,,点,,且.
连接,
,
在中
,
,
,
即,化简得
,
所以结论①正确,且定值为14;
取,,满足,此时,
若取,,同样满足,但此时,也不是定值.
因此,结论②错误.
(2)解:点,,点,,且.
,,
,
点P到x轴距离为7,到y轴距离为7,
,
,
四边形的面积:,
,
,,
,,
.
20.(1)解:,,
∴矩形的面积为.
答:矩形的面积是.
(2)解:大理石的面积为,
壁布的面积为,
则整个电视墙的总费用为(元).
答:整个电视墙需要花费元.
21.(1)解:由题意可得,,
在中,,
∴,
,
在,,
∴,
,
即供水点M到喷泉A,B需要铺设的管道总长为;
(2)解:在中,,
,
∴是直角三角形,,
,
∴喷泉B到小路的最短距离为.
22.(1)原式
,
(2)∵a ,b ,
∴,
∵,
∴,
∴,
∴,
∴2,
∵m 是正整数,
∴m=2.
(3)由得出,
∴,
∵,
∵,
∴.
23.解:()由题意得,,
∴,
故答案为:;
()∵的面积为,的面积为,同时的面积为,
∴,,,
∵,
∴是直角三角形,
故答案为:直角;
(),理由如下:
设直角三角形的三边分别为 ,
则,,,
∵,
∴;
()由图②可得,.
24.(1)证明:根据题意,,,,,
则,
四边形的面积,
,
,
;
(2)解:如图2所示,连接,过点作于点,
,,
,
四边形是矩形,
千米,千米,
千米,
(千米),
由勾股定理得:(千米),
则两个村庄之间的距离为25千米.
故答案为:25;
(3)解:如图3所示,连接,作线段的垂直平分线交于,则点即为所求;
连接,,
,
在中,由勾股定理得:,
在中,由勾股定理得:,
,
在(2)的背景下,则千米,千米,千米,
千米,
,
千米.
即的长为6.3125千米;
(4)解:如图4,,
设,则,
先作出点关于的对称点,连接,过点作于点,
则,
当点三点共线时,有最小值,
由轴对称可得:,
的最小值为,
即:就是代数式的最小值.
代数式的最小值为.
故答案为:20.
25.解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,
∵AB=AC,
∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,
∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,
∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,
∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,
在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,
∴∠ABE=30°,
∵AB=12,
∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
一.选择题(共10小题,满分30分,每小题3分)
1.若,化简的结果是( )
A. B.5 C. D.
2.如图,在,,,,以为折痕将翻折,使点与点重合,则的长为( )
A. B.1 C. D.
3.已知,则代数式的值为( )
A. B. C. D.
4.如图,已知为等腰直角三角形,则,,三者的关系为( )
A. B.
C. D.
5.如图是一个按某种规律排列的数阵:
根据数阵排列的规律,第n(n是整数,且n≥4)行从左向右数第(n-3)个数是(用含n的代数式表示)( ).
A. B. C. D.
6.已知m、n是正整数,若+是整数,则满足条件的有序数对(m,n)为( )
A.(2,5) B.(8,20) C.(2,5),(8,20) D.以上都不是
7.如图,在的正方形网格中,小正方形的边长均为1,小正方形的顶点称为格点,A,B,C,D,E,F都在格点上,以为边能构成一个直角三角形,则点F的位置有( )
A.1处 B.2处 C.3处 D.4处
8.如图,要测量池塘两岸相对的两点B,D的距离,已经测得,,,米,米,则的长为( )
A.50 B.40 C. D.
9.若和都是正整数且,和是可以合并的二次根式,下列结论中正确的个数为( )
①只存在一组和使得;
②只存在两组和使得;
③不存在和使得;
④若只存在三组和使得,则的值为49或64
A.1个 B.2个 C.3个 D.4个
10.如图,以Rt△ABC各边为边分别向外作等边三角形,编号为①、②、③,将②、①如图所示依次叠在③上,已知四边形EMNC与四边形MPQN的面积分别为9与7,则斜边BC的长为( )
A.5 B.9 C.10 D.16
二.填空题(共6小题,满分18分,每小题3分)
11.已知、满足,则 .
12.如图,有一圆柱形下水管道紧靠墙砖竖直安放,墙砖为长方形,分米,分米,该管道底面是周长为分米的圆,一只蚂蚁从点爬过管道到达,需要走的最短路程是 分米.
13.若,那么的值为 .
14.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P是边AC上一动点,把△ABP沿直线BP折叠,使得点A落在图中点A′处,当△AA′C是直角三角形时,则线段CP的长是 .
15.已知,则的值是 .
16.如图,在等腰直角的斜边上任取两点,使,记,则以为边长的三角形的形状是 .
三.解答题(共9小题,满分72分)
17.(6分)先化简,再求值:,其中.如图是小亮和小芳的解答过程.
(1)______的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质:______;
(3)先化简,再求值:,其中.
18.(6分)先观察下列等式,再回答问题:
①;
②;
③;
(1)根据上面三个等式,请猜想的结果(直接写出结果)
(2)根据上述规律,解答问题:
设,求不超过的最大整数是多少?
19.(6分)平面直角坐标系中,已知点是第一象限角平分线上的点,点,,点,,且.
(1)以下两个结论:①是一个定值;②是一个定值.其中有且只有一个结论正确,请选出来,并求出这个定值.
(2)求四边形的面积.
20.(8分)小明家正在装修,电视背景墙是矩形,其中,,中间要镶一个长为,宽为的矩形大理石图案(图中阴影部分).
(1)矩形的面积是多少?(结果化为最简二次根式)
(2)除去大理石图案部分,其他部分贴壁布,若壁布的造价为8元,大理石的造价为150元,则整个电视墙需要花费多少元?(结果化为最简二次根式)
21.(8分)如图,某小区的两个喷泉A,B位于小路的同侧,两个喷泉间的距离的长为.现要为喷泉铺设供水管道,供水点M在小路上,供水点M到的距离的长为,的长为.
(1)求供水点M到喷泉A,B需要铺设的管道总长;
(2)请求出喷泉B到小路的最短距离.
22.(9分)阅读下列材料,然后回答问题.
①在进行二次根式的化简与运算时,我们有时会碰上如一样的式子,其实我们还可以将其进一步化简: 以上这种化简的步骤叫做分母有理化.
②学习数学,最重要的是学习数学思想,其中一种数学思想叫做换元的思想,它可以简化我们的计算,比如我们熟悉的下面这个题:已知 ab2,ab 3 ,求.我们可以把ab和ab看成是一个整体,令 xab , y ab ,则.这样,我们不用求出a,b,就可以得到最后的结果.
(1)计算: ;
(2)m 是正整数, a ,b 且.求 m.
(3)已知,求的值.
23.(9分)探究一:如图,均为正方形.
问题:()若图中的为直角三角形,的面积为,的面积为,则的面积为________;
()若的面积为,的面积为,同时的面积为,则为________三角形.
探究二:图形变化:
()如图,分别以直角三角形的三边为直径向三角形外作三个半圆,判断这三个半圆的面积之间有什么关系,并说说你的理由;
()如图,如果直角三角形两直角边长分别为和,以直角三角形的三边为直径作半圆,你能利用上面的结论求出阴影部分的面积吗?如果能,请写出你的计算过程;如果不能,请说明理由.
24.(10分)【背景介绍】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明精彩粉呈,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.
【小试牛刀】(1)把两个全等的直角三角形如图1放置,,已知,,,,试证明.
【知识运用】
(2)如图2,铁路上,两点(看作直线上的两点)相距24千米,,为两个村庄(看作两个点),,,垂足分别为、,千米,千米,则两个村庄的距离为 千米(直接填空);
(3)在(2)的背景下,要在上建造一个供应站,使得,求的长.
(4)【知识迁移】借助上面的思考过程与几何模型,求代数式的最小值 .
25.(10分)我们规定,三角形任意两边的“广益值”等于第三边上的中线和这边一半的平方差.如图1,在中,是边上的中线,与的“广益值”就等于的值,可记为
(1)在中,若,,求的值.
(2)如图2,在中,,,求,的值.
(3)如图3,在中,是边上的中线,,,,求和的长.
参考答案
一.选择题
1.B
【分析】本题主要考查了二次根式有意义的条件,二次根式的性质,整式的加减.根据二次根式有意义的条件求得,推出,,据此求解即可.
【详解】解:∵,
∴,,
∴,
∴,,
∴.
故选:B.
2.A
【分析】本题考查的是勾股定理的应用,轴对称的性质,根据勾股定理可以求得,再由勾股定理列出方程即可得出答案.
【详解】解:∵在,,,,
∴,
设,则,
由折叠可知,
在中,,
∴,
∴,
∴.
∴.
故选:A
3.C
【分析】根据已知,得到,整体思想带入求值即可.
【详解】解:∵,
∴,
∴
.
故选C.
4.C
【分析】过点C作,使,连接,,证明,进而得出,,再得出是等腰直角三角形,再根据勾股定理即可得解.
【详解】解:如图,过点C作,使,连接,,
是等腰直角三角形,,
,
,
,
在和中,
,
,,
,
是等腰直角三角形,
,
在中,,
,
故选C.
5.C
【分析】观察数阵排列,可发现各数的被开方数是从1开始的连续自然数,行数中的数字个数是行数的2倍,求出n-1行的数字个数,再加上从左向右的第n-3个数,就得到所求数的被开方数,再写成算术平方根的形式即可.
【详解】由图中规律知,前(n-1)行的数据个数为2+4+6+…+2(n-1)=n(n-1),
∴第n(n是整数,且n≥4)行从左向右数第(n-3)个数的被开方数是:n(n-1)+n-3=n2-3,
∴第n(n是整数,且n≥4)行从左向右数第(n-3)个数是:
故选:C.
【点睛】本题考查了数字规律的知识;解题的关键是熟练掌握数字规律、二次根式的性质,从而完成求解.
6.C
【分析】根据二次根式的性质分析即可得出答案.
【详解】解:∵+是整数,m、n是正整数,
∴m=2,n=5或m=8,n=20,
当m=2,n=5时,原式=2是整数;
当m=8,n=20时,原式=1是整数;
即满足条件的有序数对(m,n)为(2,5)或(8,20),
故选:C.
7.B
【分析】先利用勾股定理求出的长,再根据勾股定理的逆定理,如果满足,则,即为直角三角形,解出的长满足,进而得出点F的位置.
【详解】解:由题意可得,.
∵以为边能构成一个直角三角形,且
∴,
即,
解得,
∴F点的位置如图所示,共2处.
故选:B.
8.A
【分析】本题考查的是勾股定理的应用,二次根式的化简,等腰三角形的判定,作出合适的辅助线是解本题的关键,如图,过作于,过作于,求解,,,,延长交于,则,由勾股定理可得:,可得:,,同理可得:,可得:,,,再进一步求解即可.
【详解】解:如图,过作于,过作于,
∴,,
∵,,
∴,
∵,
∴,
∴,
∵,
∴,
延长交于,则,
由勾股定理可得:,
∴,
解得:,
∴,
∴,
∴,
∴,
同理可得:,
∴,
解得:,
∴,,
∴.
故选:A
9.C
【分析】直接利用同类二次根式的定义得出和是同类二次根式,进而得出答案.
【详解】解:①和都是正整数且,和可以合并的二次根式,
,
,
当时,
故该选项①正确;
②,
当,则
当则.
故选项②正确;
③,
当时,
,所以不存在,
故该选项③正确;
④,
,
当时,,
,
,
有无数和满足等式,故该选项④错误.
故选:C.
10.C
【分析】设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,根据勾股定理得到c2+b2=a2,根据等式的性质得到c2+b2=a2.根据等边三角形的面积公式得到S3=a2,S2=c2,S1=b2,根据已知条件列方程即可得到结论.
【详解】解:如图,设等边三角形△EBC,△ABD,△ACF的面积分别是S3,S2,S1,AC=b,BC=a,AB=c,
∵△ABC是直角三角形,且∠BAC=90度,
∴c2+b2=a2,
∴c2+b2=a2.
∵S3=a2,S2=c2,S1=b2,
∴S3﹣S2=(a2﹣c2)=b2=9,S3﹣S1=a2﹣b2=(a2﹣b2)=c2=+=,
∴b=6,c=8,
即AB=8,AC=6,
∴BC===10,
故选:C.
二.填空题
11.或34
【分析】本题考查二次根式有意义的条件;根据被开方数大于等于0列式不等式,求出x,再求出y,然后代入代数式进行计算即可得解.
【详解】解:依题意,得:,
解得:;
当时,
;
∴;
当时,
;
∴;
∴的值为或34,
故答案为:或34.
12.
【分析】本题考查了勾股定理的应用最短路线问题,把圆柱侧面展开,由两点之间,线段最短,可知线段为蚂蚁爬行的最短路径,利用勾股定理计算即可求解,正确画出图形是解题的关键.
【详解】解:把圆柱侧面展开,如图,则分米,分米,
由两点之间,线段最短,可知线段为蚂蚁爬行的最短路径,
由勾股定理得,分米,
∴需要走的最短路程是分米,
故答案为:.
13.
【分析】本题考查了二次根式的混合运算、完全平方公式,熟练掌握并灵活运用完全平方公式是解题关键.利用完全平方公式将变形为,再代入的值进行运算求值即可得.
【详解】解: ,
故答案为:.
14.4或3
【分析】分类讨论分别当∠AA′C=90°时,当∠ACA′=90°时,根据折叠的性质函数直角三角形的性质即可得到结论.
【详解】解:如图1,当∠AA′C=90°时,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴AP=A′P,
∴∠PAA′=∠AA′P,
∵∠ACA′+∠PAA′=∠CA′P+∠AA′P=90°,
∴∠PCA′=∠PA′C,
∴PC=PA′,
∴PC=AC=4,
如图2,当∠ACA′=90°时,
∵在Rt△ABC中,∠ACB=90°,且AC=8,BC=6.
∴AB=10,
∵以直线BP为轴把△ABP折叠,使得点A落在图中点A′处,
∴A′B=AB=10,PA=PA′,
∴A′C=4,
设PC=x,
∴AP=8-x,
∵A′C2+PC2=PA′2,
∴42+x2=(8-x)2,
解得:x=3,
∴PC=3,
综上所述:当△AA′C是直角三角形时,则线段CP的长是4或3,
故答案为:4或3.
15.9
【分析】先将原等式变形为,再根据平方的非负性可得,,,由此可求得a、b、c的值,进而可求得答案.
【详解】解:∵,
∴,
∴,
∴,,,
∴,,,
∴,,,
∴,
故答案为:9.
16.直角三角形
【分析】本题考查等腰直角三角形的性质,难度较大,注意掌握旋下列情形常实施旋转变换:(1)图形中出现等边三角形或正方形,把旋转角分别定为、;(2)图形中有线段的中点,将图形绕中点旋转,构造中心对称全等三角形;(3)图形中出现有公共端点的线段,将含有相等线段的图形绕公共端点,旋转两相等线段的夹角后与另一相等线段重合.
把绕点逆时针旋转,得,这样就集中成一个与 相等的角,在一条直线上的、、集中为,只需判定的形状即可.
【详解】解:如图:把绕点逆时针旋转,得,
则,
,
又,
∴,
,
又,
,
∴以、、为边长的三角形的形状是直角三角形.
故答案为:直角三角形.
三.解答题
17.(1)解:当时,
原式
原式
,
小亮错误,
故答案:小亮.
(2)解:由题意得
;
故答案:.
(3)解:当时,
原式
原式
.
18.(1)解:① ;
② ;
③ ,
故.
(2)解:①
;
②
;
③
,
,……
,
故.
故不超过的最大整数是2023.
19.(1)结论①正确,理由如下:
点是第一象限角平分线上的点,
,
解得:,
,,
即点P的坐标为,
点,,点,,且.
连接,
,
在中
,
,
,
即,化简得
,
所以结论①正确,且定值为14;
取,,满足,此时,
若取,,同样满足,但此时,也不是定值.
因此,结论②错误.
(2)解:点,,点,,且.
,,
,
点P到x轴距离为7,到y轴距离为7,
,
,
四边形的面积:,
,
,,
,,
.
20.(1)解:,,
∴矩形的面积为.
答:矩形的面积是.
(2)解:大理石的面积为,
壁布的面积为,
则整个电视墙的总费用为(元).
答:整个电视墙需要花费元.
21.(1)解:由题意可得,,
在中,,
∴,
,
在,,
∴,
,
即供水点M到喷泉A,B需要铺设的管道总长为;
(2)解:在中,,
,
∴是直角三角形,,
,
∴喷泉B到小路的最短距离为.
22.(1)原式
,
(2)∵a ,b ,
∴,
∵,
∴,
∴,
∴,
∴2,
∵m 是正整数,
∴m=2.
(3)由得出,
∴,
∵,
∵,
∴.
23.解:()由题意得,,
∴,
故答案为:;
()∵的面积为,的面积为,同时的面积为,
∴,,,
∵,
∴是直角三角形,
故答案为:直角;
(),理由如下:
设直角三角形的三边分别为 ,
则,,,
∵,
∴;
()由图②可得,.
24.(1)证明:根据题意,,,,,
则,
四边形的面积,
,
,
;
(2)解:如图2所示,连接,过点作于点,
,,
,
四边形是矩形,
千米,千米,
千米,
(千米),
由勾股定理得:(千米),
则两个村庄之间的距离为25千米.
故答案为:25;
(3)解:如图3所示,连接,作线段的垂直平分线交于,则点即为所求;
连接,,
,
在中,由勾股定理得:,
在中,由勾股定理得:,
,
在(2)的背景下,则千米,千米,千米,
千米,
,
千米.
即的长为6.3125千米;
(4)解:如图4,,
设,则,
先作出点关于的对称点,连接,过点作于点,
则,
当点三点共线时,有最小值,
由轴对称可得:,
的最小值为,
即:就是代数式的最小值.
代数式的最小值为.
故答案为:20.
25.解:(1)已知如图:AO为BC上的中线,
在Rt中,
AO2-OC2=AC2
因为
所以AO2-OC2=81
所以AC2=81
所以AC=9.
(2)①如图2,取BC的中点D,连接AO,
∵AB=AC,
∴AO⊥BC,
在△ABC中,AB=AC,∠BAC=120°,
∴∠ABC=30°,
在Rt△AOB中,AB=12,∠ABC=30°,
∴AO=6,OB==,
∴ABAC=AO2﹣BO2=36﹣108=﹣72,
②取AC的中点D,连接BD,
∴AD=CD=AC=6,过点B作BE⊥AC交CA的延长线于E,
在Rt△ABE中,∠BAE=180°﹣∠BAC=60°,
∴∠ABE=30°,
∵AB=12,
∴AE=6,BE=,
∴DE=AD+AE=12,
在Rt△BED中,根据勾股定理得,BD=
∴BABC=BD2﹣CD2=216;
(3)作BD⊥CD,
因为,,
所以BD=2,
因为,是边上的中线,
所以AO2-OC2=-64,
所以OC2-AO2=64,
因为AC2=82=64,
所以OC2-AO2= AC2
所以∠OAC=90°
所以OA=
所以OC=
所以BC=2OC=2,
在Rt△BCD中,
CD=
所以AD=CD-AC=16-8=8
所以AB=
同课章节目录
