2025年中考数学二轮复习-专题6手拉手模型【课件】(共33张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题6手拉手模型【课件】(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 978.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 12:55:37 | ||
图片预览






文档简介
(共33张PPT)
专题六 手拉手模型
类型一 手拉手旋转全等
如图,在△AOB中,OA=OB,DE∥AB→将△DOE绕点O旋转
→△AOD≌△BOE.
手拉手全等模型一般可分为:双等腰三角形,双等边三角形,双
等腰直角三角形,双正方形.
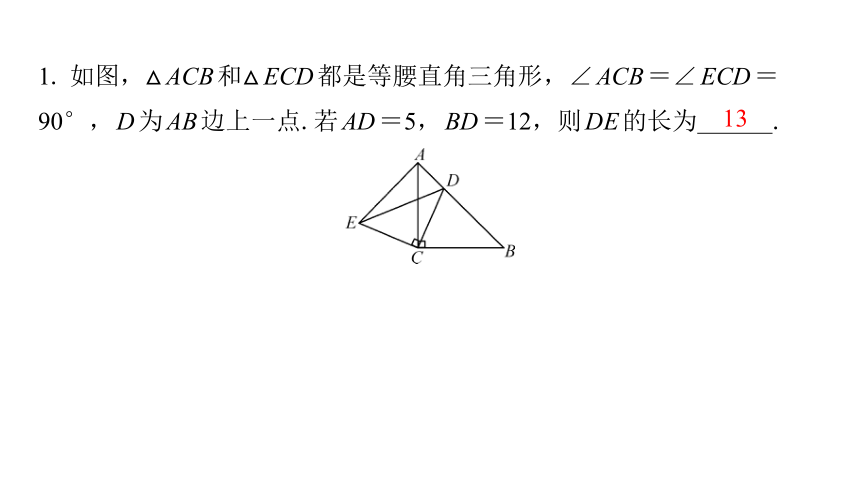
1. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=
90°,D为AB边上一点.若AD=5,BD=12,则DE的长为 .
13
2. 如图,△ABC和△CDE都是等边三角形,且点D在AB边上,AB=
5,BD=3,边BC与DE相交于点F,连接BE,则 的值是 .
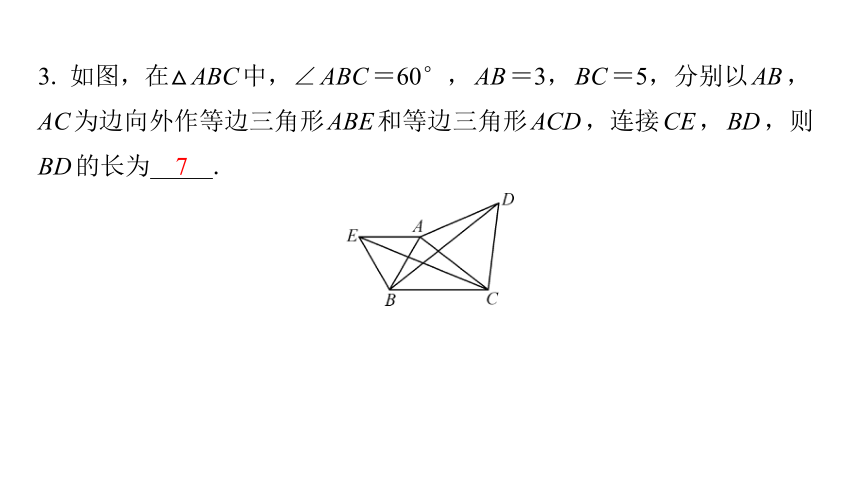
3. 如图,在△ABC中,∠ABC=60°,AB=3,BC=5,分别以AB,
AC为边向外作等边三角形ABE和等边三角形ACD,连接CE,BD,则
BD的长为 .
7
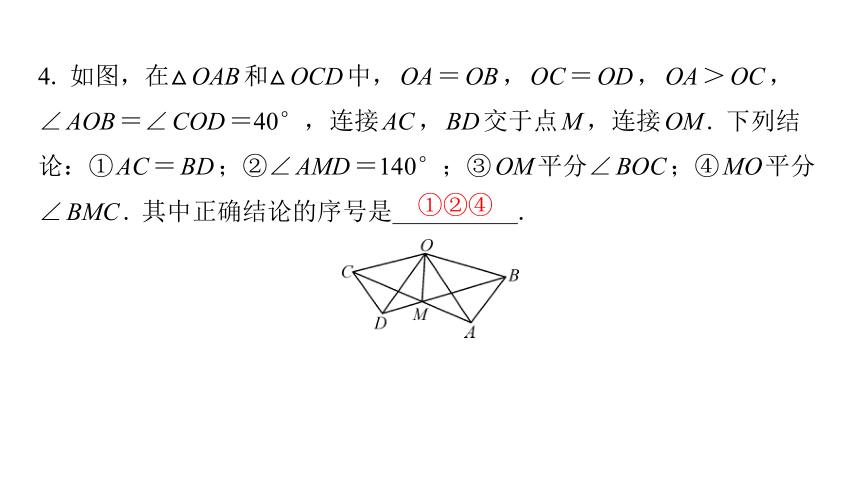
4. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,
∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM. 下列结
论:①AC=BD;②∠AMD=140°;③OM平分∠BOC;④MO平分
∠BMC. 其中正确结论的序号是 .
①②④
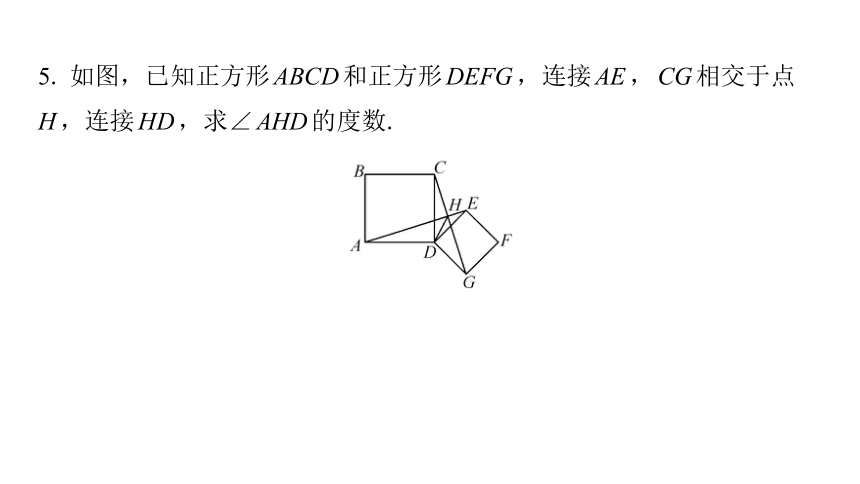
5. 如图,已知正方形ABCD和正方形DEFG,连接AE,CG相交于点
H,连接HD,求∠AHD的度数.
解:∵∠ADE=90°+∠CDE,∠CDG=90°+∠CDE,
∴∠ADE=∠CDG.
又∵AD=CD,DE=DG,∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG,∴∠AHC=∠ADC=90°.
如图,过点D作DM⊥AE于点M,DN⊥CG于点N.
∵△ADE≌△CDG,∴S△ADE=S△CDG,∴ AE·DM= CG·DN,
∴DM=DN,∴四边形DMHN是正方形,∴HD平分∠AHG,
∴∠AHD= ∠AHG=45°.
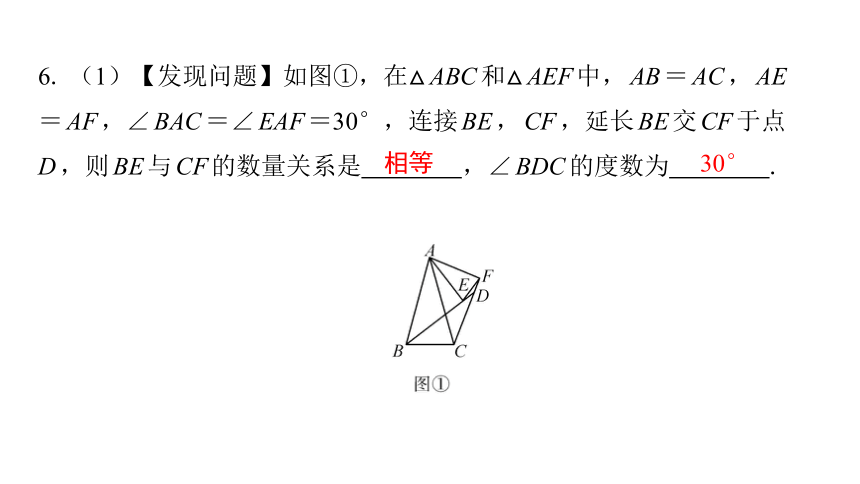
6. (1)【发现问题】如图①,在△ABC和△AEF中,AB=AC,AE
=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点
D,则BE与CF的数量关系是 ,∠BDC的度数为 .
相等
30°
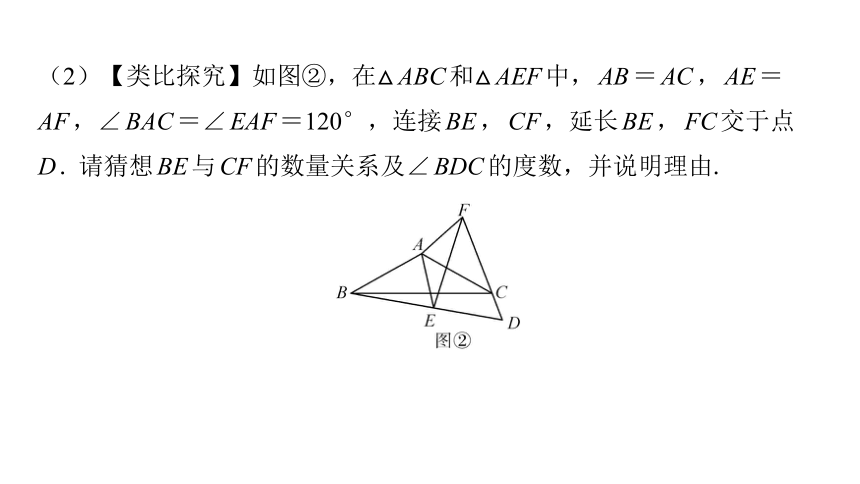
(2)【类比探究】如图②,在△ABC和△AEF中,AB=AC,AE=
AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点
D. 请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
解:(2)BE=CF,∠BDC=60°.理由如下:
∵∠BAC=∠EAF=120°,∴∠BAC-∠EAC=∠EAF-∠EAC,
∴∠BAE=∠CAF.
又∵AB=AC,AE=AF,∴△ABE≌△ACF(SAS),∴BE=CF,
∠AEB=∠AFC,
∴∠BDC=∠BEF-∠EFD=(∠AEB+∠AEF)-(∠AFC-
∠AFE),
即∠BDC=(∠AEB+30°)-(∠AFC-30°)=
∠AEB+30°-∠AFC+30°=60°.
(3)【拓展延伸】如图③,△ABC和△AEF均为等腰直角三角形,
∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线
上,过点A作AM⊥BF于点M. 请探究线段BF,CF,AM之间的数量
关系.
解:(3)∵∠BAC=∠EAF=90°,∴∠BAC-∠EAC=∠EAF-
∠EAC,∴∠BAE=∠CAF.
又∵AB=AC,AE=AF,∴△ABE≌△ACF(SAS),∴BE=CF.
∵∠EAF=90°,AE=AF,AM⊥BF,∴AM=EM=FM= EF,
∴BF=BE+EF=CF+2AM.
类型二 手拉手旋转相似
如图,在△AOB中,OA≠OB,DE∥AB→将△ODE绕点O旋转
→△AOD∽△BOE.
1. [2024·成都改编]如图,在△ABC和△ADE中,AB=AD=3,BC=
DE=4,∠ABC=∠ADE=90°,连接BD,CE,当△ADE绕点A旋
转过程中,则 的值为 .
2. 如图,在△ABC中,∠ACB=90°,∠A=60°,D,E分别是
AC,BC上一点,且DE∥AB(图①),将△DCE绕点C逆时针旋转,
使得点D恰好落在AB边上(图②).若图②中,AD= ,DB=4,
则DE的长为 .
5
3. 如图,在正方形ABCD和正方形AEFG中,连接BG,CF,则 的
值为 .
4. (1)如图①,已知△ABC∽△ADE,求证:△ABD∽△ACE;
(1)证明:∵△ABC∽△ADE,∴ = ,∠BAC=∠DAE,
∴∠BAD=∠CAE,∴△ABD∽△ACE.
(2)如图②,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC
=∠ADE=30°,点D在边BC上,AC与DE相交于点F,若 =
,求 的值.
(2)解:如图②,连接CE. 设BD=a,则AD= a.
∵∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,
∴△ABC∽△ADE. 由(1)可得△ABD∽△ACE,
∴ = =tan30°= ,∴CE= BD= a,∴ = =3.
又∵∠ADE=∠ACE=30°,∠AFD=∠EFC,
∴△ADF∽△ECF,∴ = =3.
5. [2024·江西节选]如图,在Rt△ABC中,D是斜边AB上的动点(点D
与点A不重合),连接CD,以CD为直角边在CD的右侧构造
Rt△CDE,∠DCE=90°,连接BE, = =m.
(1)如图①,当m=1时,BE与AD之间的位置关系是 ,数量
关系是 .
BE⊥AD
BE=AD
(2)如图②,当m≠1时,猜想BE与AD之间的位置关系和数量关系,
并证明猜想.
解:(2)BE⊥AD,BE=mAD. 证明如下:
∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE.
又∵ = ,∴△BCE∽△ACD,
∴ = =m,∠CBE=∠A,∴BE=mAD.
又∵∠A+∠ABC=90°,∴∠CBE+∠ABC=90°,即∠ABE=
90°,∴BE⊥AD.
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,
BF,如图③.已知AC=6,设AD=x,四边形CDFE的面积为y,求y
与x的函数解析式,并求出y的最小值.
解:(3)当m=1时,由(1)可得BE=AD=x,BE⊥AD,
∴CB=CA=6,CD=CE,∴AB= =6 ,∴BD=AB
-AD=6 -x,
∴DE2=BE2+BD2=x2+ =2x2-12 x+72.
∵点C与点F关于DE对称,∴CD=CE=EF=DF,∴四边形CDFE
是正方形,
∴y= DE2=x2-6 x+36= +18,∴当x=3 时,y
取最小值为18.
6. 如图,△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,
CB=mCA,CE=mCD,连接AD,BE.
(1)猜想AD与BE的位置关系,并说明理由;
解:(1)BE⊥AD. 理由如下:如图,延长BE交AD于点G.
∵∠BCE+∠ECA=∠ACD+∠ECA=90°,∴∠BCE=∠ACD.
∵CB=mCA,CE=mCD,∴ = = ,∴△ECB∽△DCA,
∴∠EBC=∠DAC.
∵∠CAB+∠ABG+∠EBC=90°,∴∠CAB+∠ABG+∠DAC=
90°,∴∠AGB=90°,∴BE⊥AD.
(2)当m= ,AB=4 ,DE=4时,将△CDE绕点C旋转,使
A,D,E三点恰好在同一直线上,求BE的长.
解:(2)分以下两种情况讨论:如图①,当点D在线段AE上时,
由(1)可得△ECB∽△DCA,∴ = =m= .∵DE=4,∴BE= AD= (AE-4).
由(1)可得AD⊥BE,∴∠AEB=90°,∴AE2+BE2=AB2,
即AE2+ = ,
解得AE=8或AE=-2(舍去),∴BE= (AE-4)=4 .
如图②,当点D在线段AE的延长线上时,BE= AD=
(AE+4).
同理可得AE2+ = ,解得AE=2或AE=-8
(舍去),
∴BE= (AE+4)=6 .
综上所述,BE的长为4 或6 .
谢谢观看
专题六 手拉手模型
类型一 手拉手旋转全等
如图,在△AOB中,OA=OB,DE∥AB→将△DOE绕点O旋转
→△AOD≌△BOE.
手拉手全等模型一般可分为:双等腰三角形,双等边三角形,双
等腰直角三角形,双正方形.
1. 如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=
90°,D为AB边上一点.若AD=5,BD=12,则DE的长为 .
13
2. 如图,△ABC和△CDE都是等边三角形,且点D在AB边上,AB=
5,BD=3,边BC与DE相交于点F,连接BE,则 的值是 .
3. 如图,在△ABC中,∠ABC=60°,AB=3,BC=5,分别以AB,
AC为边向外作等边三角形ABE和等边三角形ACD,连接CE,BD,则
BD的长为 .
7
4. 如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,
∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM. 下列结
论:①AC=BD;②∠AMD=140°;③OM平分∠BOC;④MO平分
∠BMC. 其中正确结论的序号是 .
①②④
5. 如图,已知正方形ABCD和正方形DEFG,连接AE,CG相交于点
H,连接HD,求∠AHD的度数.
解:∵∠ADE=90°+∠CDE,∠CDG=90°+∠CDE,
∴∠ADE=∠CDG.
又∵AD=CD,DE=DG,∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG,∴∠AHC=∠ADC=90°.
如图,过点D作DM⊥AE于点M,DN⊥CG于点N.
∵△ADE≌△CDG,∴S△ADE=S△CDG,∴ AE·DM= CG·DN,
∴DM=DN,∴四边形DMHN是正方形,∴HD平分∠AHG,
∴∠AHD= ∠AHG=45°.
6. (1)【发现问题】如图①,在△ABC和△AEF中,AB=AC,AE
=AF,∠BAC=∠EAF=30°,连接BE,CF,延长BE交CF于点
D,则BE与CF的数量关系是 ,∠BDC的度数为 .
相等
30°
(2)【类比探究】如图②,在△ABC和△AEF中,AB=AC,AE=
AF,∠BAC=∠EAF=120°,连接BE,CF,延长BE,FC交于点
D. 请猜想BE与CF的数量关系及∠BDC的度数,并说明理由.
解:(2)BE=CF,∠BDC=60°.理由如下:
∵∠BAC=∠EAF=120°,∴∠BAC-∠EAC=∠EAF-∠EAC,
∴∠BAE=∠CAF.
又∵AB=AC,AE=AF,∴△ABE≌△ACF(SAS),∴BE=CF,
∠AEB=∠AFC,
∴∠BDC=∠BEF-∠EFD=(∠AEB+∠AEF)-(∠AFC-
∠AFE),
即∠BDC=(∠AEB+30°)-(∠AFC-30°)=
∠AEB+30°-∠AFC+30°=60°.
(3)【拓展延伸】如图③,△ABC和△AEF均为等腰直角三角形,
∠BAC=∠EAF=90°,连接BE,CF,且点B,E,F在一条直线
上,过点A作AM⊥BF于点M. 请探究线段BF,CF,AM之间的数量
关系.
解:(3)∵∠BAC=∠EAF=90°,∴∠BAC-∠EAC=∠EAF-
∠EAC,∴∠BAE=∠CAF.
又∵AB=AC,AE=AF,∴△ABE≌△ACF(SAS),∴BE=CF.
∵∠EAF=90°,AE=AF,AM⊥BF,∴AM=EM=FM= EF,
∴BF=BE+EF=CF+2AM.
类型二 手拉手旋转相似
如图,在△AOB中,OA≠OB,DE∥AB→将△ODE绕点O旋转
→△AOD∽△BOE.
1. [2024·成都改编]如图,在△ABC和△ADE中,AB=AD=3,BC=
DE=4,∠ABC=∠ADE=90°,连接BD,CE,当△ADE绕点A旋
转过程中,则 的值为 .
2. 如图,在△ABC中,∠ACB=90°,∠A=60°,D,E分别是
AC,BC上一点,且DE∥AB(图①),将△DCE绕点C逆时针旋转,
使得点D恰好落在AB边上(图②).若图②中,AD= ,DB=4,
则DE的长为 .
5
3. 如图,在正方形ABCD和正方形AEFG中,连接BG,CF,则 的
值为 .
4. (1)如图①,已知△ABC∽△ADE,求证:△ABD∽△ACE;
(1)证明:∵△ABC∽△ADE,∴ = ,∠BAC=∠DAE,
∴∠BAD=∠CAE,∴△ABD∽△ACE.
(2)如图②,在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC
=∠ADE=30°,点D在边BC上,AC与DE相交于点F,若 =
,求 的值.
(2)解:如图②,连接CE. 设BD=a,则AD= a.
∵∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,
∴△ABC∽△ADE. 由(1)可得△ABD∽△ACE,
∴ = =tan30°= ,∴CE= BD= a,∴ = =3.
又∵∠ADE=∠ACE=30°,∠AFD=∠EFC,
∴△ADF∽△ECF,∴ = =3.
5. [2024·江西节选]如图,在Rt△ABC中,D是斜边AB上的动点(点D
与点A不重合),连接CD,以CD为直角边在CD的右侧构造
Rt△CDE,∠DCE=90°,连接BE, = =m.
(1)如图①,当m=1时,BE与AD之间的位置关系是 ,数量
关系是 .
BE⊥AD
BE=AD
(2)如图②,当m≠1时,猜想BE与AD之间的位置关系和数量关系,
并证明猜想.
解:(2)BE⊥AD,BE=mAD. 证明如下:
∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE.
又∵ = ,∴△BCE∽△ACD,
∴ = =m,∠CBE=∠A,∴BE=mAD.
又∵∠A+∠ABC=90°,∴∠CBE+∠ABC=90°,即∠ABE=
90°,∴BE⊥AD.
(3)在(1)的条件下,点F与点C关于DE对称,连接DF,EF,
BF,如图③.已知AC=6,设AD=x,四边形CDFE的面积为y,求y
与x的函数解析式,并求出y的最小值.
解:(3)当m=1时,由(1)可得BE=AD=x,BE⊥AD,
∴CB=CA=6,CD=CE,∴AB= =6 ,∴BD=AB
-AD=6 -x,
∴DE2=BE2+BD2=x2+ =2x2-12 x+72.
∵点C与点F关于DE对称,∴CD=CE=EF=DF,∴四边形CDFE
是正方形,
∴y= DE2=x2-6 x+36= +18,∴当x=3 时,y
取最小值为18.
6. 如图,△CAB和△CDE都是直角三角形,∠ACB=∠DCE=90°,
CB=mCA,CE=mCD,连接AD,BE.
(1)猜想AD与BE的位置关系,并说明理由;
解:(1)BE⊥AD. 理由如下:如图,延长BE交AD于点G.
∵∠BCE+∠ECA=∠ACD+∠ECA=90°,∴∠BCE=∠ACD.
∵CB=mCA,CE=mCD,∴ = = ,∴△ECB∽△DCA,
∴∠EBC=∠DAC.
∵∠CAB+∠ABG+∠EBC=90°,∴∠CAB+∠ABG+∠DAC=
90°,∴∠AGB=90°,∴BE⊥AD.
(2)当m= ,AB=4 ,DE=4时,将△CDE绕点C旋转,使
A,D,E三点恰好在同一直线上,求BE的长.
解:(2)分以下两种情况讨论:如图①,当点D在线段AE上时,
由(1)可得△ECB∽△DCA,∴ = =m= .∵DE=4,∴BE= AD= (AE-4).
由(1)可得AD⊥BE,∴∠AEB=90°,∴AE2+BE2=AB2,
即AE2+ = ,
解得AE=8或AE=-2(舍去),∴BE= (AE-4)=4 .
如图②,当点D在线段AE的延长线上时,BE= AD=
(AE+4).
同理可得AE2+ = ,解得AE=2或AE=-8
(舍去),
∴BE= (AE+4)=6 .
综上所述,BE的长为4 或6 .
谢谢观看
同课章节目录
