2024-2025学年数学八年级下册苏科版期中素养检测卷(含解析)
文档属性
| 名称 | 2024-2025学年数学八年级下册苏科版期中素养检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 20:37:14 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年数学八年级下册苏科版期中素养检测卷
一、单选题
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A. B.
C. D.
2.在的各数位中,“2”出现的频率是( )
A.6 B.4 C. D.
3.下列调查方式中,采用了抽样调查方式的是( )
A.为了确定开设几个航模课外班,调查愿意参加的学生总数
B.为了解某班级学生每天完成作业所用时间,对全班学生进行调查
C.为了给全校学生定制校服,对学生的身材进行调查
D.调查某牛奶厂生产的袋装鲜奶是否符合卫生标准
4.事件A:我市某射击运动员射击三次,刚好都射中靶心,事件B:连续掷四次一角硬币,每次都是正面朝上则( )
A.事件A和事件B都是必然事件 B.事件A是随机事件,事件B是不可能事件
C.事件A是必然事件,事件B是随机事件 D.事件A和事件B都是随机事件
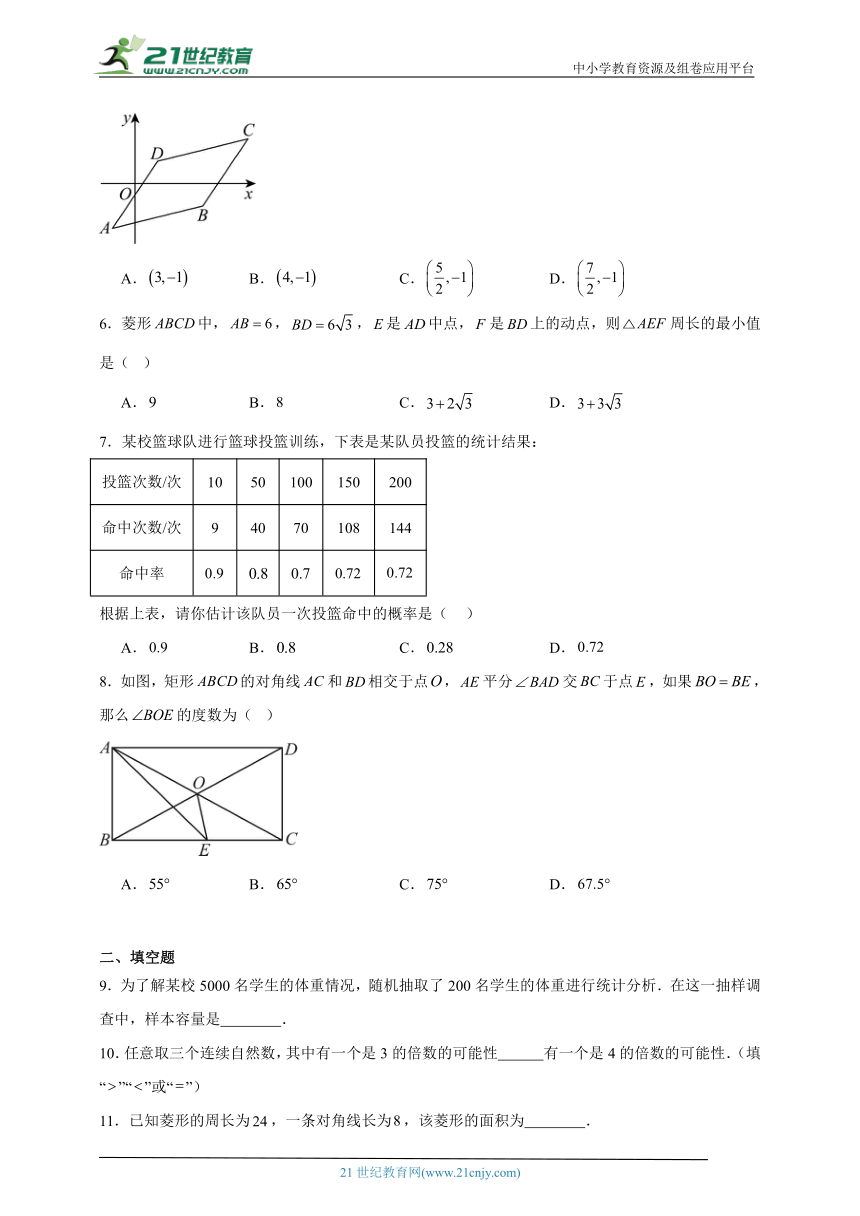
5.如图,在平面直角坐标系中,平行四边形三个顶点坐标分别为,,,则顶点B的坐标为( )
A. B. C. D.
6.菱形中,,,是中点,是上的动点,则周长的最小值是( )
A. B. C. D.
7.某校篮球队进行篮球投篮训练,下表是某队员投篮的统计结果:
投篮次数/次 10 50 100 150 200
命中次数/次 9 40 70 108 144
命中率
根据上表,请你估计该队员一次投篮命中的概率是( )
A. B. C. D.
8.如图,矩形的对角线和相交于点,平分交于点,如果,那么的度数为( )
A. B. C. D.
二、填空题
9.为了解某校5000名学生的体重情况,随机抽取了200名学生的体重进行统计分析.在这一抽样调查中,样本容量是 .
10.任意取三个连续自然数,其中有一个是3的倍数的可能性 有一个是4的倍数的可能性.(填“”“”或“”)
11.已知菱形的周长为,一条对角线长为,该菱形的面积为 .
12.数学课上老师给出时间,要求用多种方法证明某一问题,结果如表所示:
正确证法数量 0种 1种 2种 3种
人数 10 12 14 6
用 种方法给出证明的人数最多,占总人数的百分比约为 (精确到).
13.在一个盒子中有除颜色外均相同的10个红球,8个绿球和一些黑球,从里面拿出一个球,拿出绿球的可能性小于,那么至少有 个黑球.
14.如图,的对角线与相交于点.若,则的长是 .
15.如图,在矩形中,,为对角线,为的中点,过点作,与交于点,与交于点,为上一点(包含顶点,),则的最大值为 .
16.如图,在中,,,,,,都是等边三角形,下列结论中:①;②;③四边形是平行四边形;④;⑤,正确的序号是 .
三、解答题
17.小颖有20张大小相同的卡片,上面分别标有数字,她把卡片放在一个盒子中搅匀,每次从盒中抽出1张卡片,记录卡片上数字是否为3的倍数,得到如下统计表:
抽取次数n 20 40 60 80 100 120 140 160 180 200
出现3的倍数的频数m 5 13 17 26 32 36 39 49 55 61
出现3的倍数的频率(精确到0.01)
(1)填表.
(2)随着抽取次数的增加,出现3的倍数的频率会在哪个常数附近摆动?
(3)根据上表数据,从盒中任抽1张卡片,所标数字是3的倍数的概率估计值是多少?
18.如图,在中,,,垂足为,.
(1)求证:;
(2)若,,求的度数.
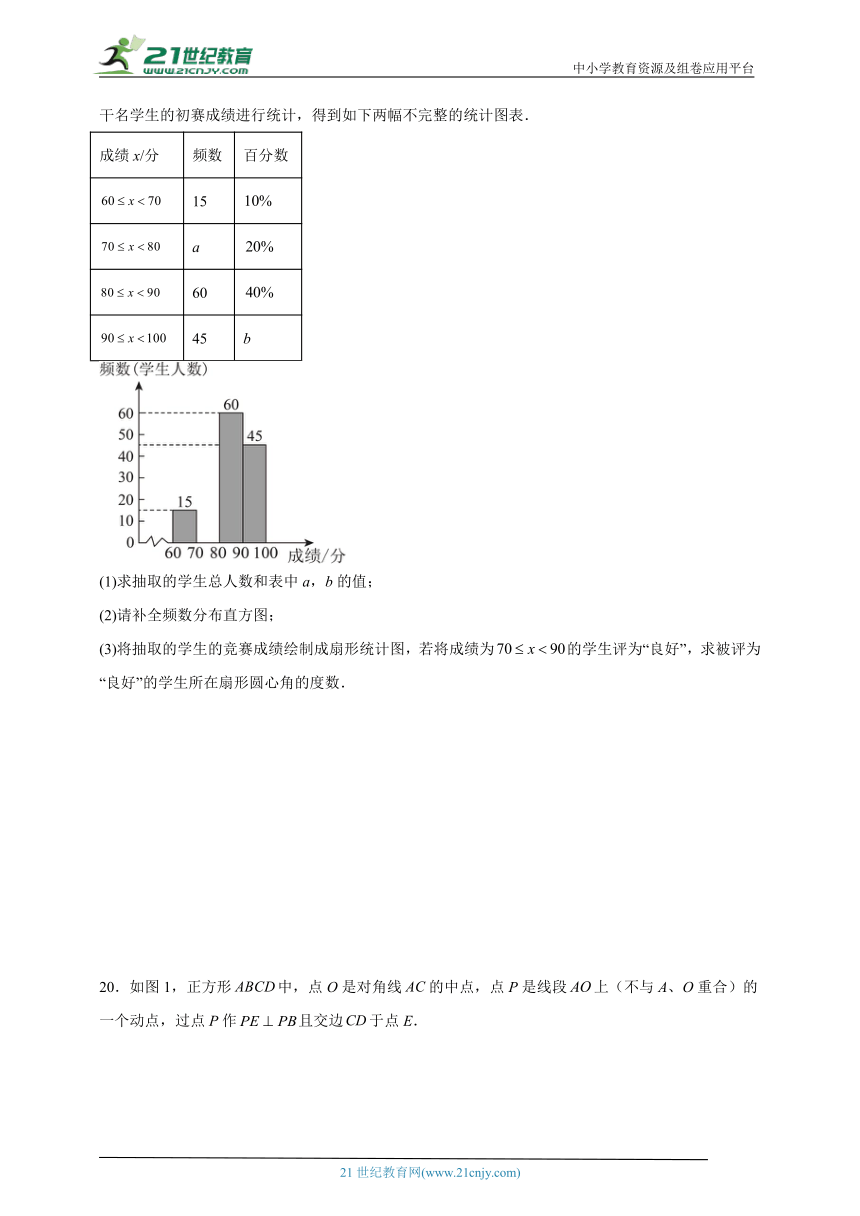
19.某校举行了水资源保护知识竞赛,为了了解本次知识竞赛成绩情况,从参赛学生中组机抽取了若干名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 百分数
15
a
60
45 b
(1)求抽取的学生总人数和表中a,b的值;
(2)请补全频数分布直方图;
(3)将抽取的学生的竞赛成绩绘制成扇形统计图,若将成绩为的学生评为“良好”,求被评为“良好”的学生所在扇形圆心角的度数.
20.如图1,正方形中,点O是对角线的中点,点P是线段上(不与A、O重合)的一个动点,过点P作且交边于点E.
(1)与相等吗?证明你的结论.
(2)过点E作于点F,如图2,若正方形的边长为2,则在点P运动的过程中,的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.
21.消防云梯主要是用于高层建筑火灾等救援任务,消防云梯的使用可以大幅提高消防救援的效率,缩短救援时间,减少救援难度和风险.如图,某栋楼房发生火灾,在这栋楼离地面24米的处有一老人需要救援,已知消防车高为4米,救人时消防车上的云梯必须伸长至最长25米.
(1)求此时消防车的位置与楼房的距离的长;
(2)完成处的救援后,消防员发现在处的上方4米的处有一小孩没有及时撤离,为了能成功地救出小孩,消防车需从处驶近到处,云梯移动至,消防车高为,问消防车靠近的距离也为4米吗?请说明理由.
22.人教版数学八年级下册教材的数学活动-----折纸,引起许多同学的兴趣.我们可以通过折纸开展数学探究,探索数学的奥秘.
(1)如图1,对折矩形纸片,使与重合,得到折痕,把纸片展平;以为折痕再一次折叠纸片,使点A落在折痕上的点N处,把纸片展平;连接.观察图1中和,猜想这三个角的关系,并说明理由;
(2)如图2,M为矩形纸片的边上的一点,连结,在上取一点P,折叠纸片,使B,P重合,展平纸片,得到折痕;折叠纸片,使点B、P分别落在上,展平纸片得到折痕l , 折痕l与交于点O, 点B、P的对应点分别为G、N,连接.证明:;
(3)如图3,矩形纸片中,, 点P是边上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F,要使折痕始终与边有交点,直接写出的取值范围.
《2024-2025学年数学八年级下册苏科版期中素养检测卷》参考答案
题号 1 2 3 4 5 6 7 8
答案 D D D D A D D C
1.D
【分析】本题主要考查了中心对称图形的定义,把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.根据中心对称图形的定义进行逐一判断即可.
【详解】解:选项A、B、C中的图案都不能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形,
选项D中的图案能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形,
故选:D.
2.D
【分析】本题考查了频数与频率,熟练掌握频率频数总次数是解题的关键.根据“频率频数总次数”计算即可解答.
【详解】解∶ 在的各数位中,“2”出现的频率是.
故选∶D.
3.D
【分析】本题考查的知识点是调查方式的选择,解题关键是掌握普查和抽样调查的概念及优缺点.
根据普查和抽样调查的概念及优缺点对选项进行逐一分析并求解即可.
【详解】解:选项,调查愿意参加的学生总数应调查所有学生,所以是普查,不符合题意,选项错误;
选项,对全班学生进行调查,是普查,不符合题意,选项错误;
选项,每个人的身材不同,应对所有学生的身材进行调查,是普查,不符合题意,选项错误;
选项,调查牛奶具有破坏性,调查牛奶适宜采用抽查,符合题意,选项正确.
故选:.
4.D
【分析】本题考查了必然事件“必然事件发生的可能性为1”与随机事件“在一定条件下,可能发生也可能不发生的事件,称为随机事件”,熟练掌握定义是解题关键.根据必然事件和随机事件的定义求解即可得.
【详解】解:我市某射击运动员射击三次,刚好都射中靶心,是随机事件,
连续掷四次一角硬币,每次都是正面朝上,是随机事件,
所以事件和事件都是随机事件,
故选:D.
5.A
【分析】本题考查了平行四边形的性质,坐标与图形性质,设点,由平行四边形的性质可得,,即可求解,掌握平行四边形的性质是本题的关键.
【详解】解:设点,
∵四边形是平行四边形,点,点,点,
∴,,
∴,,
∴点,
故选:A.
6.D
【分析】本题考查了菱形的性质、勾股定理,等边三角形的判定和性质,轴对称最短路径问题,解决本题的关键是掌握菱形的性质;
根据菱形的性质得到,,,根据勾股定理求出,根据线段垂直平分线的性质、勾股定理定理计算即可;
【详解】如图,连接,交于点,连接,
∵四边形是菱形,
,
,,,
由勾股定理得:,
,
是中点,
,
,,
,
,
根据两点之间,线段最短可知此时的周长最小,
的周长的最小值,
,
为等边三角形,
为中点,
为直角三角形,
在中,由勾股定理得:,
的周长的最小值;
故选:D
7.D
【分析】本题考查了根据评率估计概率,解题的关键是掌握经过大量重复试验,事件发生的频率会稳定在一个常数附近,这个常数等于概率.据此即可解答.
【详解】解:由表可知,经过大量重复试验,该队员一次投篮命中的频率稳定在,
∴该队员一次投篮命中的概率是,
故选:D.
8.C
【分析】本题主要考查了矩形的性质,等腰直角三角形的判定和性质,等边三角形的判定和性质,三角形内角和定理,解题的关键是熟练掌握相关的判定和性质.
根据矩形性质得出,,,,根据等腰三角形的判定得出,证明为等边三角形,得出,根据等腰三角形的性质得出即可.
【详解】解:∵四边形是矩形,
∴,,,,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴,
故选:C.
9.200
【分析】本题考查了总体、个体、样本、样本容量,解题关键是明确考查的对象,总体、个体与样本的考查对象是相同的,所不同的是范围的大小;样本容量是样本中包含的个体的数目,不能带单位.
根据样本的定义,即可求解.
【详解】解:了解某校5000名学生的体重情况,随机抽取了200名学生的体重进行统计分析,在这个问题中,样本容量是100,
故答案为:200.
10.
【分析】此题考查了可能性的大小,根据题意判断出是3的倍数的可能性和是4的倍数的可能性,进而求解即可.
【详解】∵三个连续自然数中至少有一个是3的倍数,有可能都不是4的倍数,比如:1,2,3
∴任意取三个连续自然数,其中有一个是3的倍数的可能性为1,是4的倍数的可能性为0到1
∴有一个是3的倍数的可能性有一个是4的倍数的可能性.
故答案为:.
11.
【分析】本题考查了菱形的性质和菱形的面积公式,掌握菱形的面积公式是解题的关键.因为周长是,所以边长是.根据对角线互相垂直平分得直角三角形,运用勾股定理求另一条对角线的长,最后根据菱形的面积等于对角线乘积的一半计算求解.
【详解】解:因为周长是,所以边长是.
如图所示:,.
根据菱形的性质,,,
在中,
根据勾股定理,,
.
菱形的面积为.
故答案为:.
12.
【分析】此题主要考查了利用图表信息解决实际问题,解答本题的关键是读懂题意,找出量与量之间的正确关系.
结合图象可知用两种方法证明的人数最多,结合图表可求出班级总人数,进而求出百分率.
【详解】解:由表得,用2种方法给出证明的人数最多;
,
∴占总人数的百分比约为.
故答案为:2,.
13.7
【分析】本题考查可能性的大小,先根据绿球可能性的大小得到球的总数.进而可求解.
【详解】解:∵8个绿球,绿球的可能性小于,
球的总数大于24,
至少有个黑球.
故答案为:7.
14.10
【分析】本题考查的是勾股定理的应用,平行四边形的性质,利用平行四边形的性质求解,再利用勾股定理求解,从而可得答案.
【详解】解:∵,
∴,
∵,
∴,
∴,
故答案为:10.
15.
【分析】本题考查了矩形的性质,平行线的性质,全等三角形的判定和性质,线段垂直平分线的性质,三角形三边关系,勾股定理,熟练掌握相关知识点是解题的关键.
根据题意可证明,得到,继而得到,,当三点共线(点与点)时,的值最大,即,根据勾股定理求出,即可得到答案.
【详解】解:如图,连接,
,
,
在矩形中,
,
,
,
,
,
,
当三点共线(点与点)时,的值最大,即,
,,
,
在中,,
,
,
的最大值为,
故答案为:.
16.①②③
【分析】由,,,得,则,所以,可判断①正确;由等边三角形的性质得,,,,推导出,,即可根据“”证明,可判断②正确;再证明,由,,证明四边形是平行四边形,可判断③正确;由,,求得,可判断④错误;作于点,可求得,,,则,所以,可判断⑤错误,于是得到问题的答案.
【详解】解:,,,
,,
,
是直角三角形,且,
,
故①正确;
,,都是等边三角形,
,,,,
,,
在和中,
,
,
故②正确;
,
在和中,
,
,
,
,,
四边形是平行四边形,
故③正确;
,,
,
故④错误;
作于点,则,
,
,
,,
,
,
故⑤错误,
故答案为:①②③.
【点睛】本题主要考查了勾股定理的逆定理、等边三角形的性质、全等三角形的定与性质、平行四边形的判定与性质、直角三角形中角所对的直角边等于斜边的一半等知识,证明及是解题的关键.
17.(1)0.25,0.33,0.28,0.33,0.32,0.30,0.28,0.31,0.31,0.31
(2)0.31
(3)0.31
【分析】本题主要考查了利用频率估计概率,在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.
(1)根据一一计算并填表即可.
(2)根据表格数据即可得出答案.
(3)根据频率估计概率即可.
【详解】(1)解:填表如下:
抽取次数n 20 40 60 80 100 120 140 160 180 200
出现3的倍数的频数m 5 13 17 26 32 36 39 49 55 61
出现3的倍数的频率(精确到0.01) 0.25 0.33 0.28 0.33 0.32 0.30 0.28 0.31 0.31 0.31
(2)解:根据表格数据可知随着抽取次数的增加,出现3的倍数的频率会在常数0.31附近摆动.
(3)解:∵根据表格数据可知随着抽取次数的增加,出现3的倍数的频率会在常数0.31附近摆动.
∴从盒中任抽1张卡片,所标数字是3的倍数的概率估计值是0.31.
18.(1)证明见解析
(2)
【分析】本题考查了平行四边形的性质、三角形全等的判定与性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由平行四边形的性质可得,,再证明,即可得证;
(2)由平行四边形的性质可得,求出,,计算即可得解.
【详解】(1)证明:四边形是平行四边形,
,,
,
,,
,
,
;
(2)解:四边形是平行四边形,
,
,
,
,
,
.
19.(1)150 人,30,
(2)见解析;
(3)
【分析】此题考查了频数分布直方图、频数、扇形统计图的圆心角等知识,准确计算是关键.
(1)用第一组的频数除以所占百分数得出抽取的总人数,再根据抽取的总人数与各组频数及百分数的关系求出a、b即可解答;
(2)由(1)中a的值,补全频数分布直方图即可;
(3)用乘以被评为“良好”的学生数所占的百分比即可解答.
【详解】(1)解:抽取的学生总人数为(人).
,
,
(2)解:补全频数分布直方图如下.
(3)解:被评为“良好”的学生所在扇形圆心角的度数为.
20.(1),证明见解析
(2)的长不发生变化,.
【分析】本题考查正方形的性质,全等三角形的判定和性质.根据正方形的性质添加合适的辅助线证明三角形全等是解题的关键.
(1)过点P作,根据正方形的性质和同角的余角相等,证明,即可得证.
(2)连接,根据正方形的性质,对角线垂直和同角的余角相等,证明,即可得解.
【详解】(1)证明:如图1,过点P作,交于点M,交于点N.
∵四边形是正方形,
∴
∵,
∴
∴四边形是平行四边形,
∴,
∵,
∴,
∴.
∵四边形是正方形,
∴,,
∵,
∴,
∴,
∴.
在中,,
∴是等腰直角三角形,
∴,
∴,
∴,
∴.
(2)解:在P点运动的过程中,的长度不发生变化.理由如下:
如图2,连接.
∵四边形是边长为2的正方形,
∴,
∵点O是的中点,
∴,
∴,
∴,
∴.
∴,
∴,
∴.
由(1)得:,
∴,
∴.
∵是等腰直角三角形,
∴,
∴,
即的长不发生变化,为.
21.(1)米
(2)不是,理由见解析
【分析】本题考查勾股定理的应用,矩形的性质,从题中抽象出勾股定理这一数学模型,利用勾股定理解是解题关键.
(1)根据题意得:米,米,米,四边形为矩形,结合图形,利用勾股定理求解即可;
(2)由题意得 米,米,确定米,再由(1)中结果,结合图形即可求解.
【详解】(1)解:根据题意得:米,米,米,四边形为矩形,
∴米,
∴米,
∴米;
(2)解:不是,理由如下:
由题意得 米,米,
米,
由(1)得米;
米,
即消防车从A处向着火的楼房靠近的距离为8米.
22.(1),见解析
(2)见解析
(3)
【分析】本题考查了折叠的性质,勾股定理,等边三角形的判定和性质,作出正确辅助线是解题的关键.
(1)利用折叠的性质,可得是等边三角形,即可得到,即可证明;
(2)连接,证明,可得,即可求得,即可解答;
(3)当F、D重合时,的值最小,当E、B重合时,的值最大,利用折叠的性质和勾股定理即可解答.
【详解】(1)解:
理由如下:
由折叠可知:直线是线段的垂直平分线,
,
对折至,折痕为,
,,
,
是等边三角形,
,
∴,
∵四边形为矩形,
,
,
∴;
(2)解:如图,连接,
∵四边形是矩形,是折痕,
,
∴,
由折叠的性质可知,,,
在和中,
,
,
∴
∵
∴
∴
∵
∴
(3)解: 如图,当F、D重合时,的值最小,
根据折叠的性质知:,
在中,,
则,
此时的最小值为;
如图,当E、B重合时,的值最大,
根据折叠的性质知:,即的最大值为4.
综上,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年数学八年级下册苏科版期中素养检测卷
一、单选题
1.中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )
A. B.
C. D.
2.在的各数位中,“2”出现的频率是( )
A.6 B.4 C. D.
3.下列调查方式中,采用了抽样调查方式的是( )
A.为了确定开设几个航模课外班,调查愿意参加的学生总数
B.为了解某班级学生每天完成作业所用时间,对全班学生进行调查
C.为了给全校学生定制校服,对学生的身材进行调查
D.调查某牛奶厂生产的袋装鲜奶是否符合卫生标准
4.事件A:我市某射击运动员射击三次,刚好都射中靶心,事件B:连续掷四次一角硬币,每次都是正面朝上则( )
A.事件A和事件B都是必然事件 B.事件A是随机事件,事件B是不可能事件
C.事件A是必然事件,事件B是随机事件 D.事件A和事件B都是随机事件
5.如图,在平面直角坐标系中,平行四边形三个顶点坐标分别为,,,则顶点B的坐标为( )
A. B. C. D.
6.菱形中,,,是中点,是上的动点,则周长的最小值是( )
A. B. C. D.
7.某校篮球队进行篮球投篮训练,下表是某队员投篮的统计结果:
投篮次数/次 10 50 100 150 200
命中次数/次 9 40 70 108 144
命中率
根据上表,请你估计该队员一次投篮命中的概率是( )
A. B. C. D.
8.如图,矩形的对角线和相交于点,平分交于点,如果,那么的度数为( )
A. B. C. D.
二、填空题
9.为了解某校5000名学生的体重情况,随机抽取了200名学生的体重进行统计分析.在这一抽样调查中,样本容量是 .
10.任意取三个连续自然数,其中有一个是3的倍数的可能性 有一个是4的倍数的可能性.(填“”“”或“”)
11.已知菱形的周长为,一条对角线长为,该菱形的面积为 .
12.数学课上老师给出时间,要求用多种方法证明某一问题,结果如表所示:
正确证法数量 0种 1种 2种 3种
人数 10 12 14 6
用 种方法给出证明的人数最多,占总人数的百分比约为 (精确到).
13.在一个盒子中有除颜色外均相同的10个红球,8个绿球和一些黑球,从里面拿出一个球,拿出绿球的可能性小于,那么至少有 个黑球.
14.如图,的对角线与相交于点.若,则的长是 .
15.如图,在矩形中,,为对角线,为的中点,过点作,与交于点,与交于点,为上一点(包含顶点,),则的最大值为 .
16.如图,在中,,,,,,都是等边三角形,下列结论中:①;②;③四边形是平行四边形;④;⑤,正确的序号是 .
三、解答题
17.小颖有20张大小相同的卡片,上面分别标有数字,她把卡片放在一个盒子中搅匀,每次从盒中抽出1张卡片,记录卡片上数字是否为3的倍数,得到如下统计表:
抽取次数n 20 40 60 80 100 120 140 160 180 200
出现3的倍数的频数m 5 13 17 26 32 36 39 49 55 61
出现3的倍数的频率(精确到0.01)
(1)填表.
(2)随着抽取次数的增加,出现3的倍数的频率会在哪个常数附近摆动?
(3)根据上表数据,从盒中任抽1张卡片,所标数字是3的倍数的概率估计值是多少?
18.如图,在中,,,垂足为,.
(1)求证:;
(2)若,,求的度数.
19.某校举行了水资源保护知识竞赛,为了了解本次知识竞赛成绩情况,从参赛学生中组机抽取了若干名学生的初赛成绩进行统计,得到如下两幅不完整的统计图表.
成绩x/分 频数 百分数
15
a
60
45 b
(1)求抽取的学生总人数和表中a,b的值;
(2)请补全频数分布直方图;
(3)将抽取的学生的竞赛成绩绘制成扇形统计图,若将成绩为的学生评为“良好”,求被评为“良好”的学生所在扇形圆心角的度数.
20.如图1,正方形中,点O是对角线的中点,点P是线段上(不与A、O重合)的一个动点,过点P作且交边于点E.
(1)与相等吗?证明你的结论.
(2)过点E作于点F,如图2,若正方形的边长为2,则在点P运动的过程中,的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由.
21.消防云梯主要是用于高层建筑火灾等救援任务,消防云梯的使用可以大幅提高消防救援的效率,缩短救援时间,减少救援难度和风险.如图,某栋楼房发生火灾,在这栋楼离地面24米的处有一老人需要救援,已知消防车高为4米,救人时消防车上的云梯必须伸长至最长25米.
(1)求此时消防车的位置与楼房的距离的长;
(2)完成处的救援后,消防员发现在处的上方4米的处有一小孩没有及时撤离,为了能成功地救出小孩,消防车需从处驶近到处,云梯移动至,消防车高为,问消防车靠近的距离也为4米吗?请说明理由.
22.人教版数学八年级下册教材的数学活动-----折纸,引起许多同学的兴趣.我们可以通过折纸开展数学探究,探索数学的奥秘.
(1)如图1,对折矩形纸片,使与重合,得到折痕,把纸片展平;以为折痕再一次折叠纸片,使点A落在折痕上的点N处,把纸片展平;连接.观察图1中和,猜想这三个角的关系,并说明理由;
(2)如图2,M为矩形纸片的边上的一点,连结,在上取一点P,折叠纸片,使B,P重合,展平纸片,得到折痕;折叠纸片,使点B、P分别落在上,展平纸片得到折痕l , 折痕l与交于点O, 点B、P的对应点分别为G、N,连接.证明:;
(3)如图3,矩形纸片中,, 点P是边上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F,要使折痕始终与边有交点,直接写出的取值范围.
《2024-2025学年数学八年级下册苏科版期中素养检测卷》参考答案
题号 1 2 3 4 5 6 7 8
答案 D D D D A D D C
1.D
【分析】本题主要考查了中心对称图形的定义,把一个图形绕着某一个点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.根据中心对称图形的定义进行逐一判断即可.
【详解】解:选项A、B、C中的图案都不能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以不是中心对称图形,
选项D中的图案能找到一个点,使图形绕某一点旋转后与原来的图形重合,所以是中心对称图形,
故选:D.
2.D
【分析】本题考查了频数与频率,熟练掌握频率频数总次数是解题的关键.根据“频率频数总次数”计算即可解答.
【详解】解∶ 在的各数位中,“2”出现的频率是.
故选∶D.
3.D
【分析】本题考查的知识点是调查方式的选择,解题关键是掌握普查和抽样调查的概念及优缺点.
根据普查和抽样调查的概念及优缺点对选项进行逐一分析并求解即可.
【详解】解:选项,调查愿意参加的学生总数应调查所有学生,所以是普查,不符合题意,选项错误;
选项,对全班学生进行调查,是普查,不符合题意,选项错误;
选项,每个人的身材不同,应对所有学生的身材进行调查,是普查,不符合题意,选项错误;
选项,调查牛奶具有破坏性,调查牛奶适宜采用抽查,符合题意,选项正确.
故选:.
4.D
【分析】本题考查了必然事件“必然事件发生的可能性为1”与随机事件“在一定条件下,可能发生也可能不发生的事件,称为随机事件”,熟练掌握定义是解题关键.根据必然事件和随机事件的定义求解即可得.
【详解】解:我市某射击运动员射击三次,刚好都射中靶心,是随机事件,
连续掷四次一角硬币,每次都是正面朝上,是随机事件,
所以事件和事件都是随机事件,
故选:D.
5.A
【分析】本题考查了平行四边形的性质,坐标与图形性质,设点,由平行四边形的性质可得,,即可求解,掌握平行四边形的性质是本题的关键.
【详解】解:设点,
∵四边形是平行四边形,点,点,点,
∴,,
∴,,
∴点,
故选:A.
6.D
【分析】本题考查了菱形的性质、勾股定理,等边三角形的判定和性质,轴对称最短路径问题,解决本题的关键是掌握菱形的性质;
根据菱形的性质得到,,,根据勾股定理求出,根据线段垂直平分线的性质、勾股定理定理计算即可;
【详解】如图,连接,交于点,连接,
∵四边形是菱形,
,
,,,
由勾股定理得:,
,
是中点,
,
,,
,
,
根据两点之间,线段最短可知此时的周长最小,
的周长的最小值,
,
为等边三角形,
为中点,
为直角三角形,
在中,由勾股定理得:,
的周长的最小值;
故选:D
7.D
【分析】本题考查了根据评率估计概率,解题的关键是掌握经过大量重复试验,事件发生的频率会稳定在一个常数附近,这个常数等于概率.据此即可解答.
【详解】解:由表可知,经过大量重复试验,该队员一次投篮命中的频率稳定在,
∴该队员一次投篮命中的概率是,
故选:D.
8.C
【分析】本题主要考查了矩形的性质,等腰直角三角形的判定和性质,等边三角形的判定和性质,三角形内角和定理,解题的关键是熟练掌握相关的判定和性质.
根据矩形性质得出,,,,根据等腰三角形的判定得出,证明为等边三角形,得出,根据等腰三角形的性质得出即可.
【详解】解:∵四边形是矩形,
∴,,,,
∴,
∵平分,
∴,
∴,
∴,
∵,
∴,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴,
故选:C.
9.200
【分析】本题考查了总体、个体、样本、样本容量,解题关键是明确考查的对象,总体、个体与样本的考查对象是相同的,所不同的是范围的大小;样本容量是样本中包含的个体的数目,不能带单位.
根据样本的定义,即可求解.
【详解】解:了解某校5000名学生的体重情况,随机抽取了200名学生的体重进行统计分析,在这个问题中,样本容量是100,
故答案为:200.
10.
【分析】此题考查了可能性的大小,根据题意判断出是3的倍数的可能性和是4的倍数的可能性,进而求解即可.
【详解】∵三个连续自然数中至少有一个是3的倍数,有可能都不是4的倍数,比如:1,2,3
∴任意取三个连续自然数,其中有一个是3的倍数的可能性为1,是4的倍数的可能性为0到1
∴有一个是3的倍数的可能性有一个是4的倍数的可能性.
故答案为:.
11.
【分析】本题考查了菱形的性质和菱形的面积公式,掌握菱形的面积公式是解题的关键.因为周长是,所以边长是.根据对角线互相垂直平分得直角三角形,运用勾股定理求另一条对角线的长,最后根据菱形的面积等于对角线乘积的一半计算求解.
【详解】解:因为周长是,所以边长是.
如图所示:,.
根据菱形的性质,,,
在中,
根据勾股定理,,
.
菱形的面积为.
故答案为:.
12.
【分析】此题主要考查了利用图表信息解决实际问题,解答本题的关键是读懂题意,找出量与量之间的正确关系.
结合图象可知用两种方法证明的人数最多,结合图表可求出班级总人数,进而求出百分率.
【详解】解:由表得,用2种方法给出证明的人数最多;
,
∴占总人数的百分比约为.
故答案为:2,.
13.7
【分析】本题考查可能性的大小,先根据绿球可能性的大小得到球的总数.进而可求解.
【详解】解:∵8个绿球,绿球的可能性小于,
球的总数大于24,
至少有个黑球.
故答案为:7.
14.10
【分析】本题考查的是勾股定理的应用,平行四边形的性质,利用平行四边形的性质求解,再利用勾股定理求解,从而可得答案.
【详解】解:∵,
∴,
∵,
∴,
∴,
故答案为:10.
15.
【分析】本题考查了矩形的性质,平行线的性质,全等三角形的判定和性质,线段垂直平分线的性质,三角形三边关系,勾股定理,熟练掌握相关知识点是解题的关键.
根据题意可证明,得到,继而得到,,当三点共线(点与点)时,的值最大,即,根据勾股定理求出,即可得到答案.
【详解】解:如图,连接,
,
,
在矩形中,
,
,
,
,
,
,
当三点共线(点与点)时,的值最大,即,
,,
,
在中,,
,
,
的最大值为,
故答案为:.
16.①②③
【分析】由,,,得,则,所以,可判断①正确;由等边三角形的性质得,,,,推导出,,即可根据“”证明,可判断②正确;再证明,由,,证明四边形是平行四边形,可判断③正确;由,,求得,可判断④错误;作于点,可求得,,,则,所以,可判断⑤错误,于是得到问题的答案.
【详解】解:,,,
,,
,
是直角三角形,且,
,
故①正确;
,,都是等边三角形,
,,,,
,,
在和中,
,
,
故②正确;
,
在和中,
,
,
,
,,
四边形是平行四边形,
故③正确;
,,
,
故④错误;
作于点,则,
,
,
,,
,
,
故⑤错误,
故答案为:①②③.
【点睛】本题主要考查了勾股定理的逆定理、等边三角形的性质、全等三角形的定与性质、平行四边形的判定与性质、直角三角形中角所对的直角边等于斜边的一半等知识,证明及是解题的关键.
17.(1)0.25,0.33,0.28,0.33,0.32,0.30,0.28,0.31,0.31,0.31
(2)0.31
(3)0.31
【分析】本题主要考查了利用频率估计概率,在同样条件下,做大量的重复试验,利用一个随机事件发生的频率逐渐稳定到某个常数,可以估计这个事件发生的概率.
(1)根据一一计算并填表即可.
(2)根据表格数据即可得出答案.
(3)根据频率估计概率即可.
【详解】(1)解:填表如下:
抽取次数n 20 40 60 80 100 120 140 160 180 200
出现3的倍数的频数m 5 13 17 26 32 36 39 49 55 61
出现3的倍数的频率(精确到0.01) 0.25 0.33 0.28 0.33 0.32 0.30 0.28 0.31 0.31 0.31
(2)解:根据表格数据可知随着抽取次数的增加,出现3的倍数的频率会在常数0.31附近摆动.
(3)解:∵根据表格数据可知随着抽取次数的增加,出现3的倍数的频率会在常数0.31附近摆动.
∴从盒中任抽1张卡片,所标数字是3的倍数的概率估计值是0.31.
18.(1)证明见解析
(2)
【分析】本题考查了平行四边形的性质、三角形全等的判定与性质,熟练掌握以上知识点并灵活运用是解此题的关键.
(1)由平行四边形的性质可得,,再证明,即可得证;
(2)由平行四边形的性质可得,求出,,计算即可得解.
【详解】(1)证明:四边形是平行四边形,
,,
,
,,
,
,
;
(2)解:四边形是平行四边形,
,
,
,
,
,
.
19.(1)150 人,30,
(2)见解析;
(3)
【分析】此题考查了频数分布直方图、频数、扇形统计图的圆心角等知识,准确计算是关键.
(1)用第一组的频数除以所占百分数得出抽取的总人数,再根据抽取的总人数与各组频数及百分数的关系求出a、b即可解答;
(2)由(1)中a的值,补全频数分布直方图即可;
(3)用乘以被评为“良好”的学生数所占的百分比即可解答.
【详解】(1)解:抽取的学生总人数为(人).
,
,
(2)解:补全频数分布直方图如下.
(3)解:被评为“良好”的学生所在扇形圆心角的度数为.
20.(1),证明见解析
(2)的长不发生变化,.
【分析】本题考查正方形的性质,全等三角形的判定和性质.根据正方形的性质添加合适的辅助线证明三角形全等是解题的关键.
(1)过点P作,根据正方形的性质和同角的余角相等,证明,即可得证.
(2)连接,根据正方形的性质,对角线垂直和同角的余角相等,证明,即可得解.
【详解】(1)证明:如图1,过点P作,交于点M,交于点N.
∵四边形是正方形,
∴
∵,
∴
∴四边形是平行四边形,
∴,
∵,
∴,
∴.
∵四边形是正方形,
∴,,
∵,
∴,
∴,
∴.
在中,,
∴是等腰直角三角形,
∴,
∴,
∴,
∴.
(2)解:在P点运动的过程中,的长度不发生变化.理由如下:
如图2,连接.
∵四边形是边长为2的正方形,
∴,
∵点O是的中点,
∴,
∴,
∴,
∴.
∴,
∴,
∴.
由(1)得:,
∴,
∴.
∵是等腰直角三角形,
∴,
∴,
即的长不发生变化,为.
21.(1)米
(2)不是,理由见解析
【分析】本题考查勾股定理的应用,矩形的性质,从题中抽象出勾股定理这一数学模型,利用勾股定理解是解题关键.
(1)根据题意得:米,米,米,四边形为矩形,结合图形,利用勾股定理求解即可;
(2)由题意得 米,米,确定米,再由(1)中结果,结合图形即可求解.
【详解】(1)解:根据题意得:米,米,米,四边形为矩形,
∴米,
∴米,
∴米;
(2)解:不是,理由如下:
由题意得 米,米,
米,
由(1)得米;
米,
即消防车从A处向着火的楼房靠近的距离为8米.
22.(1),见解析
(2)见解析
(3)
【分析】本题考查了折叠的性质,勾股定理,等边三角形的判定和性质,作出正确辅助线是解题的关键.
(1)利用折叠的性质,可得是等边三角形,即可得到,即可证明;
(2)连接,证明,可得,即可求得,即可解答;
(3)当F、D重合时,的值最小,当E、B重合时,的值最大,利用折叠的性质和勾股定理即可解答.
【详解】(1)解:
理由如下:
由折叠可知:直线是线段的垂直平分线,
,
对折至,折痕为,
,,
,
是等边三角形,
,
∴,
∵四边形为矩形,
,
,
∴;
(2)解:如图,连接,
∵四边形是矩形,是折痕,
,
∴,
由折叠的性质可知,,,
在和中,
,
,
∴
∵
∴
∴
∵
∴
(3)解: 如图,当F、D重合时,的值最小,
根据折叠的性质知:,
在中,,
则,
此时的最小值为;
如图,当E、B重合时,的值最大,
根据折叠的性质知:,即的最大值为4.
综上,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
