湖南省永州市祁阳市茅竹镇中心学校2024-2025学年下学期期中监测八年级下册《数学》试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市茅竹镇中心学校2024-2025学年下学期期中监测八年级下册《数学》试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 963.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览



文档简介
湖南省祁阳市茅竹镇中心学校2024-2025学年下学期期中监测《数学》试卷
考试时间:120分钟 满分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.以下列各组数据为三角形的三边长,可以构成直角三角形的是( )
A.1,2,5 B.6,12,13 C.6,8,10 D.12,20,25
2.如图是计算器上显示的数字“2023”,说法正确的是( )
A.是轴对称图形但不是中心对称图形 B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形 D.不是轴对称图形也不是中心对称图形
3.如图,在菱形ABCD中,∠BEF=α°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PFC=( )
A. B.90°﹣α° C.180°﹣2α° D.180°﹣3α°
第2题图 第3题图 第4题图 第5题图
4.如图,四边形ABCD中,AD=BC,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AD∥BC B.∠A+∠B=180° C.∠A=∠C D.AB=CD
5.如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,若AB=3,AD=4,则EF的长是( )
A.1 B.2 C.2.5 D.3
6.如图,在四边形ABCD中,E,F分别是AD,BC的中点,AB=4,CD=6,则EF的取值范围是( )
A.1<EF≤5 B.1≤EF≤5 C.4<EF≤6 D.4≤EF≤6
7.下列说法正确的是( )
A.平行四边形的邻边平行且相等 B.矩形的对角线互相垂直
C.菱形的四个内角都是直角 D.正方形的两条对角线互相垂直平分且相等
8.在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=3:7:4;③∠A=90°﹣∠B;④∠A=∠B∠C中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①④ C.①②③ D.①②③④
9.如图,点E在平行四边形ABCD内部,AF∥BE,DF∥CE,设平行四边形ABCD的面积为S1,四边形AEDF的面积为S2,则的值是( )
A. B. C.1 D.2
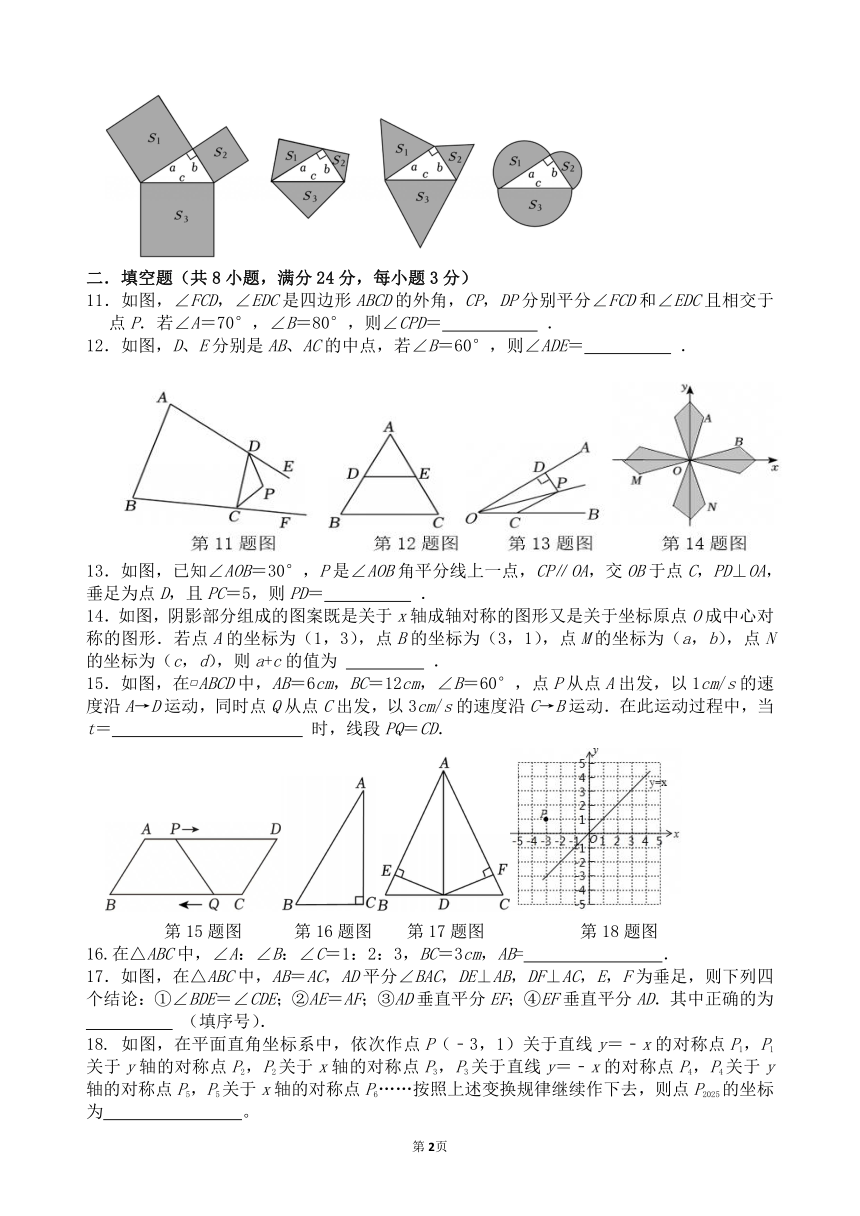
10.如图,以直角三角形的三边a,b,c为边,向外作正方形,等腰直角三角形,等边三角形和半圆,上述四种情况的面积关系满足S1+S2=S3的图形有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分24分,每小题3分)
11.如图,∠FCD,∠EDC是四边形ABCD的外角,CP,DP分别平分∠FCD和∠EDC且相交于点P.若∠A=70°,∠B=80°,则∠CPD= .
12.如图,D、E分别是AB、AC的中点,若∠B=60°,则∠ADE= .
13.如图,已知∠AOB=30°,P是∠AOB角平分线上一点,CP∥OA,交OB于点C,PD⊥OA,垂足为点D,且PC=5,则PD= .
14.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标为(1,3),点B的坐标为(3,1),点M的坐标为(a,b),点N的坐标为(c,d),则a+c的值为 .
15.如图,在 ABCD中,AB=6cm,BC=12cm,∠B=60°,点P从点A出发,以1cm/s的速度沿A→D运动,同时点Q从点C出发,以3cm/s的速度沿C→B运动.在此运动过程中,当t= 时,线段PQ=CD.
第15题图 第16题图 第17题图 第18题图
16.在△ABC中,∠A:∠B:∠C=1:2:3,BC=3cm,AB= .
17.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:①∠BDE=∠CDE;②AE=AF;③AD垂直平分EF;④EF垂直平分AD.其中正确的为
(填序号).
18. 如图,在平面直角坐标系中,依次作点P(﹣3,1)关于直线y=﹣x的对称点P1,P1关于y轴的对称点P2,P2关于x轴的对称点P3,P3关于直线y=﹣x的对称点P4,P4关于y轴的对称点P5,P5关于x轴的对称点P6……按照上述变换规律继续作下去,则点P2025的坐标为 。
三.解答题(共9小题,满分66分)
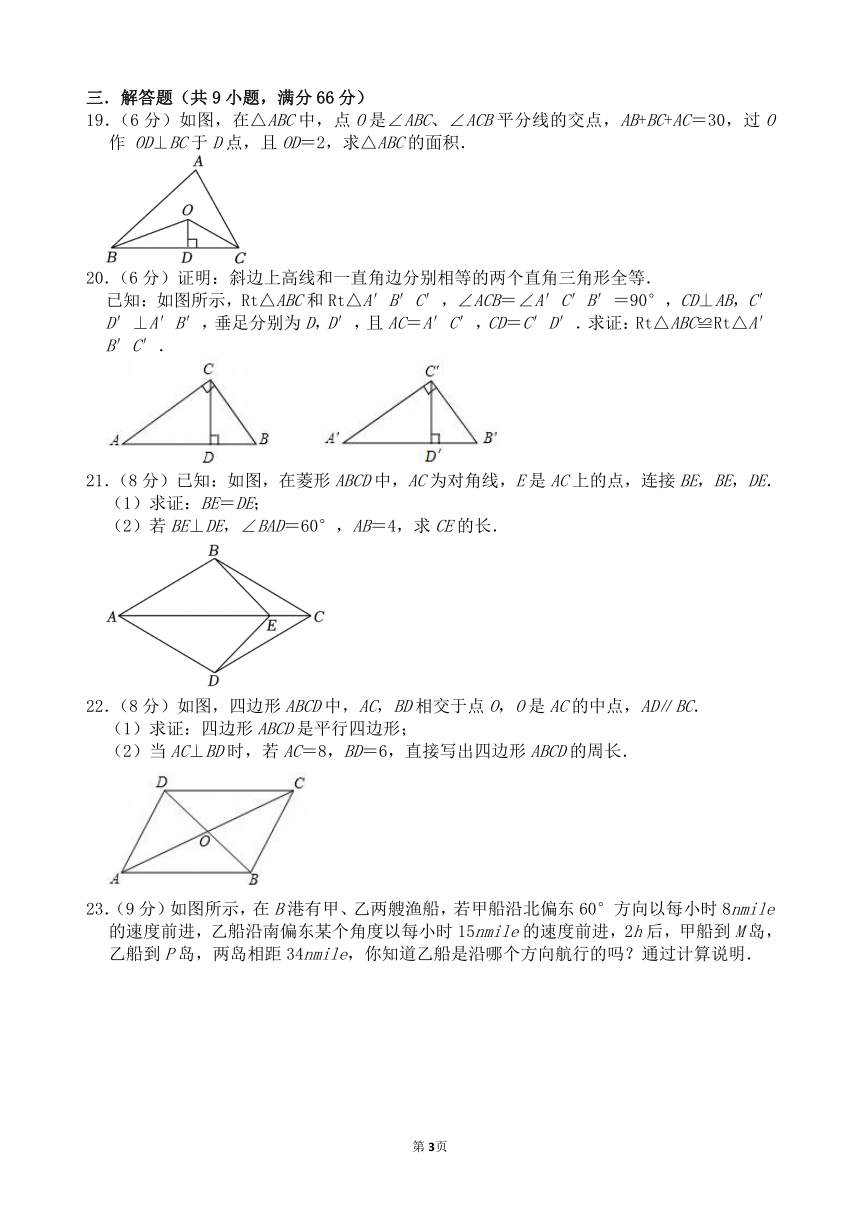
19.(6分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=30,过O作 OD⊥BC于D点,且OD=2,求△ABC的面积.
20.(6分)证明:斜边上高线和一直角边分别相等的两个直角三角形全等.
已知:如图所示,Rt△ABC和Rt△A′B′C′,∠ACB=∠A′C′B′=90°,CD⊥AB,C′D′⊥A′B′,垂足分别为D,D′,且AC=A′C′,CD=C′D′.求证:Rt△ABC≌Rt△A′B′C′.
21.(8分)已知:如图,在菱形ABCD中,AC为对角线,E是AC上的点,连接BE,BE,DE.
(1)求证:BE=DE;
(2)若BE⊥DE,∠BAD=60°,AB=4,求CE的长.
22.(8分)如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
(1)求证:四边形ABCD是平行四边形;
(2)当AC⊥BD时,若AC=8,BD=6,直接写出四边形ABCD的周长.
23.(9分)如图所示,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8nmile的速度前进,乙船沿南偏东某个角度以每小时15nmile的速度前进,2h后,甲船到M岛,乙船到P岛,两岛相距34nmile,你知道乙船是沿哪个方向航行的吗?通过计算说明.
24.(8分)如图,在平行四边形ABCD中,线段AC的垂直平分线分别交AC、BC、AD于O、E、F,连接AE,CF.
(1)证明:四边形AECF是菱形;
(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=3,求四边形AECF的面积.
25.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,E为CD的中点,连接OE并延长到点F,使得OE=EF,连接CF,DF.
(1)求证:四边形OCFD是矩形;
(2)若AB=5,sin∠DOF,求BD的长.
26.(14分)已知在平面直角坐标系中,点A,C分别是x轴和y轴上的动点,∠ACB=90°,AC=BC.
(1)如图1,过点B作BE⊥x轴,交x轴于点E,交AC的延长线于点F,BC交x轴于点D,若AD=10,求BF的长;
(2)如图2,当点C运动到原点O时,∠BAO的平分线交y轴于点E,点F为线段OA上一点将△BOF沿EF翻折,FO的对应边的延长线交AB于点G,H为线段AG上一点,且BF=EH,试判断线段HG、FG、OF之间的数量关系并证明你的结论;
(3)如图3,若A(﹣6,0),C(0,3),在坐标平面内是否存在一点P(不与点C重合),使△PBC与△ABC全等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C B B D D D D
11.105°.12.60°.13.2.5.14.﹣2.
15.或3.16.6cm.17.①②③.18.(1,﹣3)
19.解:作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
由条件可知OE=OD,OF=OD,即OE=OF=OD=2,∴ =30.
20.证明:∵CD、C′D′分别是△ABC和△A′B′C′的高,
∴CD⊥AB,C′D′⊥A′B′,
∴△ACD和△A′C′D′为直角三角形.
∵Rt△ACD和Rt△A′C′D′中,
,
∴Rt△ACD≌Rt△A′C′D′(HL),
∴∠CAB=∠C′A′B′.
∵Rt△ABC和Rt△A′B′C′中,
,
∴Rt△ABC≌Rt△A′B′C′(ASA).
21.(1)证明:∵四边形ABCD是菱形,
∴CB=CD,∠BCE=∠DCE,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE;
(2)解:如图2,连接BD交AC于点O,
∵四边形ABCD是菱形,AB=4,
∴AB=AD,AO=OC,OB=ODBD,AC⊥BD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=4,OB=OD=2,OC=OA2,
∵BE⊥DE,
∴OE=OB=OD=2,
∴CE=OC﹣OE=22.
22.(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
∵O是AC的中点,
∴OA=OC.
在△AOD和△COB中,
,
∴△AOD≌△COB(AAS),
∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴BC=CD=AD=AB,OAAC=4,OBBD=3,
在Rt△AOB中,由勾股定理得:AB5,
∴四边形ABCD的周长=4AB=4×5=20.
23.解:对图形进行角标注.
甲船航行的距离BM=8×2=16(海里),
乙船航行的距离BP=15×2=30(海里),
∵MP2=342=1156,BM2+BP2=162+302=1156,
∴MP2=BM2+BP2,
∴△BMP为直角三角形,且∠MBP=90°.
∵∠MBP=90°,∠1=60°,
∴∠2=180°﹣∠1﹣∠MBP=30°,
故乙船航行的方向是南偏东30°.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE,
∵EF是线段AC的垂直平分线,
∴OA=OC,EF⊥AC,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,
∴CE=AE=3,OA=OC,OB=OD,
∵AC⊥AB,
∴EF∥AB,
∴∠OEC=∠B=30°,
∴OCCE=1.5,OEOC,
∴AC=2OC=3,EF=2OE=3,
∴四边形AECF的面积AC×EF3×3.
25.(1)证明:∵E为CD的中点,∴EC=ED.∵EF=EO,
∴四边形OCFD是平行四边形,∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°,∴四边形OCFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AB=5,BD=2OD,
∵四边形OCFD是矩形,
∴OF=CD=5,∠ODF=90°,OC=DF,
∵sin∠DOF,
即,
∴OC=DF=3,
在Rt△COD中,由勾股定理得:OD4,
∴BD=2OD=2×4=8.
26.解:(1)∵BE⊥x轴,∠ACB=90°,
∴∠AEF=∠ACB=90°,
∴∠CBF+∠F=∠FAE+∠F,
∴∠CBF=∠FAE,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA),
∴BF=AD=10;
(2)FG+HG=2FO;
证明:连接EG,EA,过点E作EM⊥AB于点M,过点E作EN⊥FG于点N,
由折叠的性质可得:∠EFO=∠EFN,
∵∠EFO=∠EFN,EM⊥AB,EO⊥FO,
∴EO=EN,
∵AE为∠BAO的角平分线,EM⊥AB,EO⊥FO,
∴∠HME=∠FOE=90°,EM=EO,
∴EO=EN=EM,
在Rt△ENG和Rt△EMG中,
,
∴Rt△ENG≌Rt△EMG(HL),
∴GN=GM,
在Rt△ENF和Rt△EMH中,
,
∴Rt△ENF≌Rt△EMH(HL),
∴FN=HM,
∴FG+HG=FN+GN+HG=FN+GM+HG=FN+HM=2FN,
在Rt△EFO和Rt△EFN中,
,
∴Rt△EFO≌Rt△EFN(HL),
∴FN=FO,
∴FG+HG=2FO;
(3)在坐标平面内存在一点P(不与点C重合),使△PBC与△ABC全等;P点的坐标为:(6,6),(9,0),(﹣3,﹣6);理由如下:
∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵△PBC与△ABC全等,
∴△PBC是等腰直角三角形,
如图3,△ACB≌△PCB,
过点C作x轴的平行线MN,过点A,P分别作MN的垂线,垂足分别为M,N,
∴∠M=∠N=90°,∵A(﹣6,0),C(0,3),∴MC=OC=3,MC=AO=6,
∵△ACB≌△PCB,∴AC=PC,在△MCA和△NCP中,
,∴△MCA≌△NCP(AAS),∴CN=MC=6,PN=MA=3,∴P(6,6),
如图4,△ACB≌△PBC,∴∠BCP=∠ABC=45°,∴∠ACP=45°,∴PC平分∠ACB,
∴PC⊥AB且PC平分AB,∴PA=PB,∵AC=BC=PB,∴AP=AC,
又∵∠PBA=∠PBC﹣∠ABC=90°﹣45°=45°,∴△ABP是等腰直角三角形,
∴∠PAB=45°,∴∠PAC=∠PAB+∠BAC=90°,
如图4,过点A作y轴的平行线DE,过点C,P分别作DE的垂线,垂足分别为D,E,
∴∠PAE=90°﹣∠DAC=∠DCA,∠E=∠D=90°,在△AEP和△CDA中,
,∴△AEP≌△CDA(AAS),∴AD=EP=3,AE=DC=6,
∴P(﹣3,﹣6),如图5,△ABC≌△CPB,
过点B分别作x,y轴的垂线,垂足分别为F,E,∴∠BFP=∠COA,∵△ABC≌△CPB,∠ACB=90°,AC=BC,∴∠ACB=∠PBC,∴AC∥PB,∴∠CAO=∠BPF(AAS),∵AC=BC=PB,
∴△ACO≌△PBF(AAS),∴BF=CO=3,PF=AO=6,∵∠ECB=90°﹣∠ACO=∠CAO,AC=BC,∠AOC=∠CEB,
∴△AOC≌△CEB(AAS),∴BE=CO=3,∴OP=OF+FP=9,∴P(9,0).综上所述,在坐标平面内存在一点P(不与点C重合),使△PBC与△ABC全等;P点的坐标为:(6,6),(9,0),(﹣3,﹣6).
声
第3页
考试时间:120分钟 满分:120分
一.选择题(共10小题,满分30分,每小题3分)
1.以下列各组数据为三角形的三边长,可以构成直角三角形的是( )
A.1,2,5 B.6,12,13 C.6,8,10 D.12,20,25
2.如图是计算器上显示的数字“2023”,说法正确的是( )
A.是轴对称图形但不是中心对称图形 B.是中心对称图形但不是轴对称图形
C.既是轴对称图形又是中心对称图形 D.不是轴对称图形也不是中心对称图形
3.如图,在菱形ABCD中,∠BEF=α°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠PFC=( )
A. B.90°﹣α° C.180°﹣2α° D.180°﹣3α°
第2题图 第3题图 第4题图 第5题图
4.如图,四边形ABCD中,AD=BC,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AD∥BC B.∠A+∠B=180° C.∠A=∠C D.AB=CD
5.如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,若AB=3,AD=4,则EF的长是( )
A.1 B.2 C.2.5 D.3
6.如图,在四边形ABCD中,E,F分别是AD,BC的中点,AB=4,CD=6,则EF的取值范围是( )
A.1<EF≤5 B.1≤EF≤5 C.4<EF≤6 D.4≤EF≤6
7.下列说法正确的是( )
A.平行四边形的邻边平行且相等 B.矩形的对角线互相垂直
C.菱形的四个内角都是直角 D.正方形的两条对角线互相垂直平分且相等
8.在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=3:7:4;③∠A=90°﹣∠B;④∠A=∠B∠C中,能确定△ABC是直角三角形的条件有( )
A.①③ B.①④ C.①②③ D.①②③④
9.如图,点E在平行四边形ABCD内部,AF∥BE,DF∥CE,设平行四边形ABCD的面积为S1,四边形AEDF的面积为S2,则的值是( )
A. B. C.1 D.2
10.如图,以直角三角形的三边a,b,c为边,向外作正方形,等腰直角三角形,等边三角形和半圆,上述四种情况的面积关系满足S1+S2=S3的图形有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题,满分24分,每小题3分)
11.如图,∠FCD,∠EDC是四边形ABCD的外角,CP,DP分别平分∠FCD和∠EDC且相交于点P.若∠A=70°,∠B=80°,则∠CPD= .
12.如图,D、E分别是AB、AC的中点,若∠B=60°,则∠ADE= .
13.如图,已知∠AOB=30°,P是∠AOB角平分线上一点,CP∥OA,交OB于点C,PD⊥OA,垂足为点D,且PC=5,则PD= .
14.如图,阴影部分组成的图案既是关于x轴成轴对称的图形又是关于坐标原点O成中心对称的图形.若点A的坐标为(1,3),点B的坐标为(3,1),点M的坐标为(a,b),点N的坐标为(c,d),则a+c的值为 .
15.如图,在 ABCD中,AB=6cm,BC=12cm,∠B=60°,点P从点A出发,以1cm/s的速度沿A→D运动,同时点Q从点C出发,以3cm/s的速度沿C→B运动.在此运动过程中,当t= 时,线段PQ=CD.
第15题图 第16题图 第17题图 第18题图
16.在△ABC中,∠A:∠B:∠C=1:2:3,BC=3cm,AB= .
17.如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E,F为垂足,则下列四个结论:①∠BDE=∠CDE;②AE=AF;③AD垂直平分EF;④EF垂直平分AD.其中正确的为
(填序号).
18. 如图,在平面直角坐标系中,依次作点P(﹣3,1)关于直线y=﹣x的对称点P1,P1关于y轴的对称点P2,P2关于x轴的对称点P3,P3关于直线y=﹣x的对称点P4,P4关于y轴的对称点P5,P5关于x轴的对称点P6……按照上述变换规律继续作下去,则点P2025的坐标为 。
三.解答题(共9小题,满分66分)
19.(6分)如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=30,过O作 OD⊥BC于D点,且OD=2,求△ABC的面积.
20.(6分)证明:斜边上高线和一直角边分别相等的两个直角三角形全等.
已知:如图所示,Rt△ABC和Rt△A′B′C′,∠ACB=∠A′C′B′=90°,CD⊥AB,C′D′⊥A′B′,垂足分别为D,D′,且AC=A′C′,CD=C′D′.求证:Rt△ABC≌Rt△A′B′C′.
21.(8分)已知:如图,在菱形ABCD中,AC为对角线,E是AC上的点,连接BE,BE,DE.
(1)求证:BE=DE;
(2)若BE⊥DE,∠BAD=60°,AB=4,求CE的长.
22.(8分)如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
(1)求证:四边形ABCD是平行四边形;
(2)当AC⊥BD时,若AC=8,BD=6,直接写出四边形ABCD的周长.
23.(9分)如图所示,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8nmile的速度前进,乙船沿南偏东某个角度以每小时15nmile的速度前进,2h后,甲船到M岛,乙船到P岛,两岛相距34nmile,你知道乙船是沿哪个方向航行的吗?通过计算说明.
24.(8分)如图,在平行四边形ABCD中,线段AC的垂直平分线分别交AC、BC、AD于O、E、F,连接AE,CF.
(1)证明:四边形AECF是菱形;
(2)在(1)的条件下,如果AC⊥AB,∠B=30°,AE=3,求四边形AECF的面积.
25.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,E为CD的中点,连接OE并延长到点F,使得OE=EF,连接CF,DF.
(1)求证:四边形OCFD是矩形;
(2)若AB=5,sin∠DOF,求BD的长.
26.(14分)已知在平面直角坐标系中,点A,C分别是x轴和y轴上的动点,∠ACB=90°,AC=BC.
(1)如图1,过点B作BE⊥x轴,交x轴于点E,交AC的延长线于点F,BC交x轴于点D,若AD=10,求BF的长;
(2)如图2,当点C运动到原点O时,∠BAO的平分线交y轴于点E,点F为线段OA上一点将△BOF沿EF翻折,FO的对应边的延长线交AB于点G,H为线段AG上一点,且BF=EH,试判断线段HG、FG、OF之间的数量关系并证明你的结论;
(3)如图3,若A(﹣6,0),C(0,3),在坐标平面内是否存在一点P(不与点C重合),使△PBC与△ABC全等?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C B B D D D D
11.105°.12.60°.13.2.5.14.﹣2.
15.或3.16.6cm.17.①②③.18.(1,﹣3)
19.解:作OE⊥AB于E,OF⊥AC于F,连接OA,如图,
由条件可知OE=OD,OF=OD,即OE=OF=OD=2,∴ =30.
20.证明:∵CD、C′D′分别是△ABC和△A′B′C′的高,
∴CD⊥AB,C′D′⊥A′B′,
∴△ACD和△A′C′D′为直角三角形.
∵Rt△ACD和Rt△A′C′D′中,
,
∴Rt△ACD≌Rt△A′C′D′(HL),
∴∠CAB=∠C′A′B′.
∵Rt△ABC和Rt△A′B′C′中,
,
∴Rt△ABC≌Rt△A′B′C′(ASA).
21.(1)证明:∵四边形ABCD是菱形,
∴CB=CD,∠BCE=∠DCE,
∵CE=CE,
∴△BCE≌△DCE(SAS),
∴BE=DE;
(2)解:如图2,连接BD交AC于点O,
∵四边形ABCD是菱形,AB=4,
∴AB=AD,AO=OC,OB=ODBD,AC⊥BD,
∵∠BAD=60°,
∴△ABD是等边三角形,
∴BD=AB=4,OB=OD=2,OC=OA2,
∵BE⊥DE,
∴OE=OB=OD=2,
∴CE=OC﹣OE=22.
22.(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
∵O是AC的中点,
∴OA=OC.
在△AOD和△COB中,
,
∴△AOD≌△COB(AAS),
∴OD=OB.
∵OA=OC,
∴四边形ABCD是平行四边形;
(2)解:∵四边形ABCD是平行四边形,
又∵AC⊥BD,
∴四边形ABCD是菱形,
∴BC=CD=AD=AB,OAAC=4,OBBD=3,
在Rt△AOB中,由勾股定理得:AB5,
∴四边形ABCD的周长=4AB=4×5=20.
23.解:对图形进行角标注.
甲船航行的距离BM=8×2=16(海里),
乙船航行的距离BP=15×2=30(海里),
∵MP2=342=1156,BM2+BP2=162+302=1156,
∴MP2=BM2+BP2,
∴△BMP为直角三角形,且∠MBP=90°.
∵∠MBP=90°,∠1=60°,
∴∠2=180°﹣∠1﹣∠MBP=30°,
故乙船航行的方向是南偏东30°.
24.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠OAF=∠OCE,
∵EF是线段AC的垂直平分线,
∴OA=OC,EF⊥AC,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∴四边形AECF是平行四边形,
又∵EF⊥AC,
∴四边形AECF是菱形;
(2)解:由(1)得:四边形AECF是菱形,EF⊥AC,
∴CE=AE=3,OA=OC,OB=OD,
∵AC⊥AB,
∴EF∥AB,
∴∠OEC=∠B=30°,
∴OCCE=1.5,OEOC,
∴AC=2OC=3,EF=2OE=3,
∴四边形AECF的面积AC×EF3×3.
25.(1)证明:∵E为CD的中点,∴EC=ED.∵EF=EO,
∴四边形OCFD是平行四边形,∵四边形ABCD是菱形,
∴AC⊥BD,∴∠DOC=90°,∴四边形OCFD是矩形;
(2)解:∵四边形ABCD是菱形,
∴CD=AB=5,BD=2OD,
∵四边形OCFD是矩形,
∴OF=CD=5,∠ODF=90°,OC=DF,
∵sin∠DOF,
即,
∴OC=DF=3,
在Rt△COD中,由勾股定理得:OD4,
∴BD=2OD=2×4=8.
26.解:(1)∵BE⊥x轴,∠ACB=90°,
∴∠AEF=∠ACB=90°,
∴∠CBF+∠F=∠FAE+∠F,
∴∠CBF=∠FAE,
在△ACD和△BCF中,
,
∴△ACD≌△BCF(ASA),
∴BF=AD=10;
(2)FG+HG=2FO;
证明:连接EG,EA,过点E作EM⊥AB于点M,过点E作EN⊥FG于点N,
由折叠的性质可得:∠EFO=∠EFN,
∵∠EFO=∠EFN,EM⊥AB,EO⊥FO,
∴EO=EN,
∵AE为∠BAO的角平分线,EM⊥AB,EO⊥FO,
∴∠HME=∠FOE=90°,EM=EO,
∴EO=EN=EM,
在Rt△ENG和Rt△EMG中,
,
∴Rt△ENG≌Rt△EMG(HL),
∴GN=GM,
在Rt△ENF和Rt△EMH中,
,
∴Rt△ENF≌Rt△EMH(HL),
∴FN=HM,
∴FG+HG=FN+GN+HG=FN+GM+HG=FN+HM=2FN,
在Rt△EFO和Rt△EFN中,
,
∴Rt△EFO≌Rt△EFN(HL),
∴FN=FO,
∴FG+HG=2FO;
(3)在坐标平面内存在一点P(不与点C重合),使△PBC与△ABC全等;P点的坐标为:(6,6),(9,0),(﹣3,﹣6);理由如下:
∵∠ACB=90°,AC=BC,
∴△ABC是等腰直角三角形,
∵△PBC与△ABC全等,
∴△PBC是等腰直角三角形,
如图3,△ACB≌△PCB,
过点C作x轴的平行线MN,过点A,P分别作MN的垂线,垂足分别为M,N,
∴∠M=∠N=90°,∵A(﹣6,0),C(0,3),∴MC=OC=3,MC=AO=6,
∵△ACB≌△PCB,∴AC=PC,在△MCA和△NCP中,
,∴△MCA≌△NCP(AAS),∴CN=MC=6,PN=MA=3,∴P(6,6),
如图4,△ACB≌△PBC,∴∠BCP=∠ABC=45°,∴∠ACP=45°,∴PC平分∠ACB,
∴PC⊥AB且PC平分AB,∴PA=PB,∵AC=BC=PB,∴AP=AC,
又∵∠PBA=∠PBC﹣∠ABC=90°﹣45°=45°,∴△ABP是等腰直角三角形,
∴∠PAB=45°,∴∠PAC=∠PAB+∠BAC=90°,
如图4,过点A作y轴的平行线DE,过点C,P分别作DE的垂线,垂足分别为D,E,
∴∠PAE=90°﹣∠DAC=∠DCA,∠E=∠D=90°,在△AEP和△CDA中,
,∴△AEP≌△CDA(AAS),∴AD=EP=3,AE=DC=6,
∴P(﹣3,﹣6),如图5,△ABC≌△CPB,
过点B分别作x,y轴的垂线,垂足分别为F,E,∴∠BFP=∠COA,∵△ABC≌△CPB,∠ACB=90°,AC=BC,∴∠ACB=∠PBC,∴AC∥PB,∴∠CAO=∠BPF(AAS),∵AC=BC=PB,
∴△ACO≌△PBF(AAS),∴BF=CO=3,PF=AO=6,∵∠ECB=90°﹣∠ACO=∠CAO,AC=BC,∠AOC=∠CEB,
∴△AOC≌△CEB(AAS),∴BE=CO=3,∴OP=OF+FP=9,∴P(9,0).综上所述,在坐标平面内存在一点P(不与点C重合),使△PBC与△ABC全等;P点的坐标为:(6,6),(9,0),(﹣3,﹣6).
声
第3页
同课章节目录
