平行四边形的判定
图片预览

文档简介
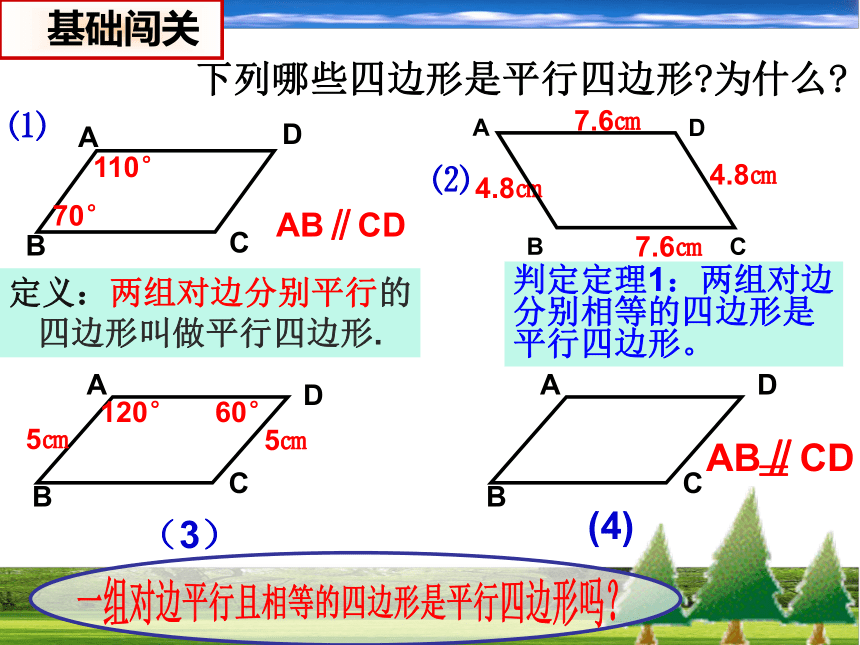
课件16张PPT。平行四边形的判定2下列哪些四边形是平行四边形?为什么? 基础闯关定义:两组对边分别平行的
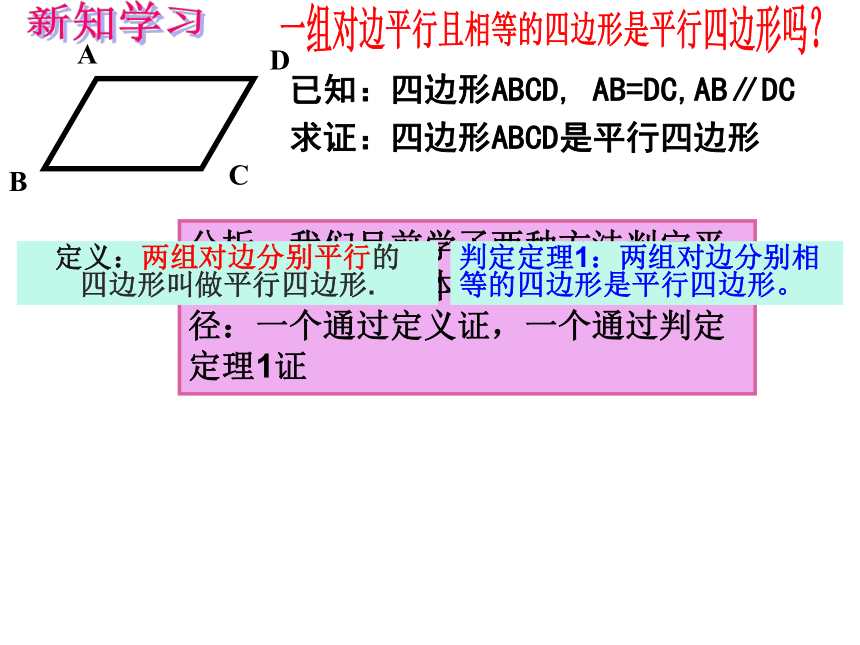
四边形叫做平行四边形.判定定理1:两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形吗?BDAC已知:四边形ABCD, AB=DC,AB∥DC
求证:四边形ABCD是平行四边形新知学习分析:我们目前学了两种方法判定平行四边形,所以本题的证明有两个途径:一个通过定义证,一个通过判定定理1证定义:两组对边分别平行的
四边形叫做平行四边形.判定定理1:两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形吗?BDAC已知:四边形ABCD, AB=CD,AB∥DC
求证:四边形ABCD是平行四边形新知学习一组对边平行且相等的四边形是平行四边形吗?
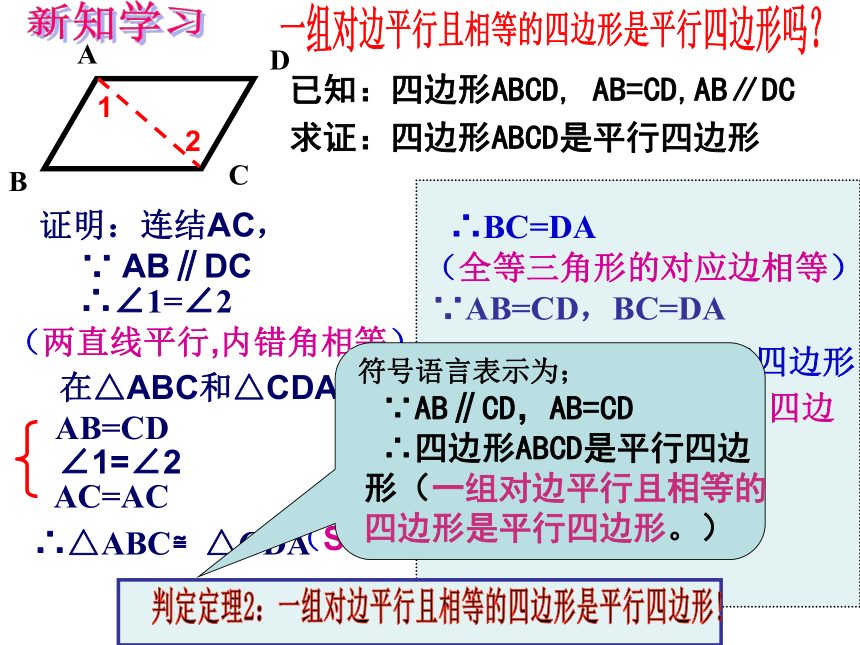
在△ABC和△CDA中 AB=CD
∠1=∠2
AC=AC ∴△ABC≌△CDA(SAS)证明:连结AC,∵ AB∥DC∴∠1=∠212(两直线平行,内错角相等)∴∠BCA=∠DAC(两组对边分别平行的四边
形是平行四边形)∴AD∥BC∴四边形ABCD是平行四边形(全等三角形的对应角相等)(内错角相等,两直线平行)∴BC=DA(两组对边分别相等的四边
形是平行四边形)∵AB=CD,BC=DA∴四边形ABCD是平行四边形(全等三角形的对应边相等)判定定理2:一组对边平行且相等的四边形是平行四边形!符号语言表示为; ∵AB∥CD,AB=CD
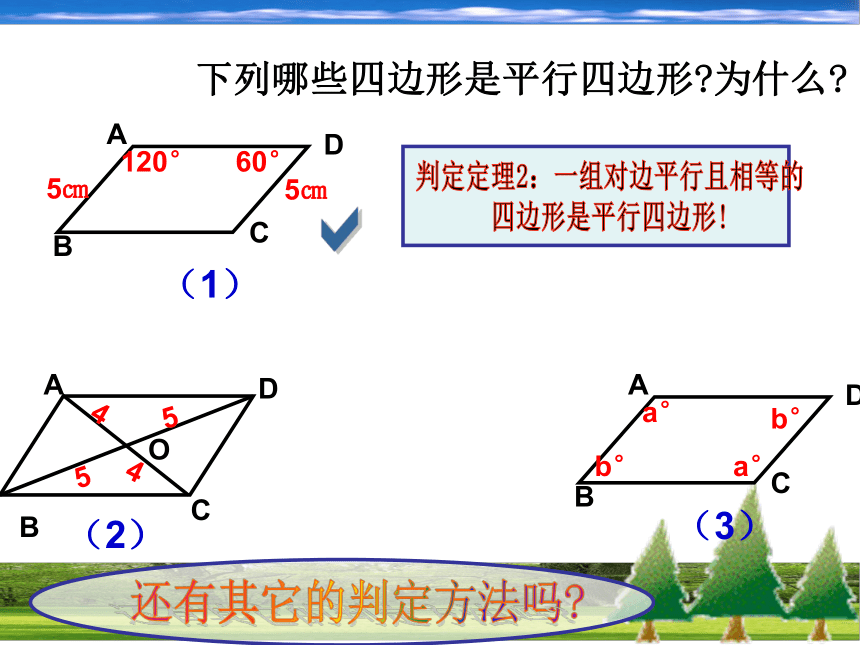
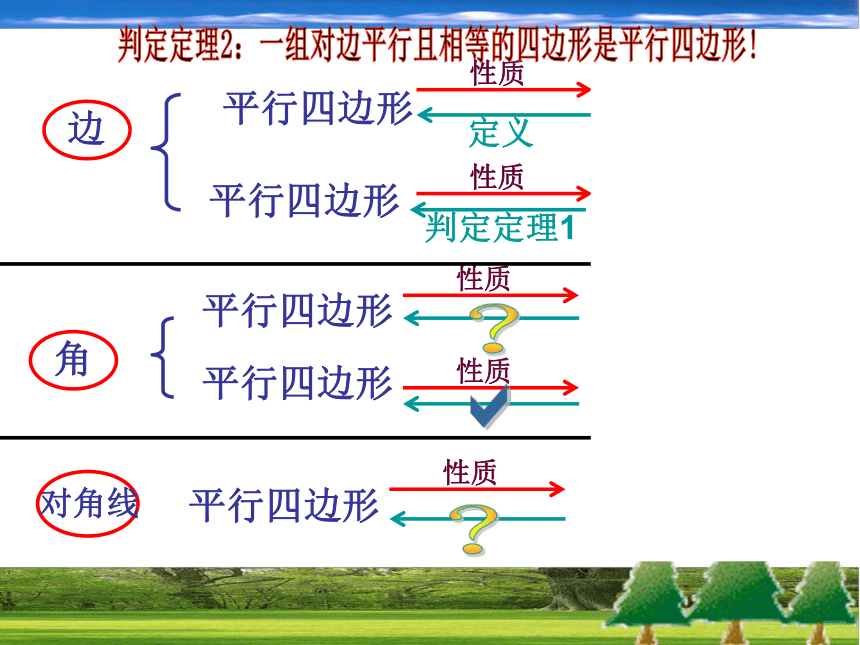
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。) 下列哪些四边形是平行四边形?为什么?还有其它的判定方法吗?判定定理2:一组对边平行且相等的
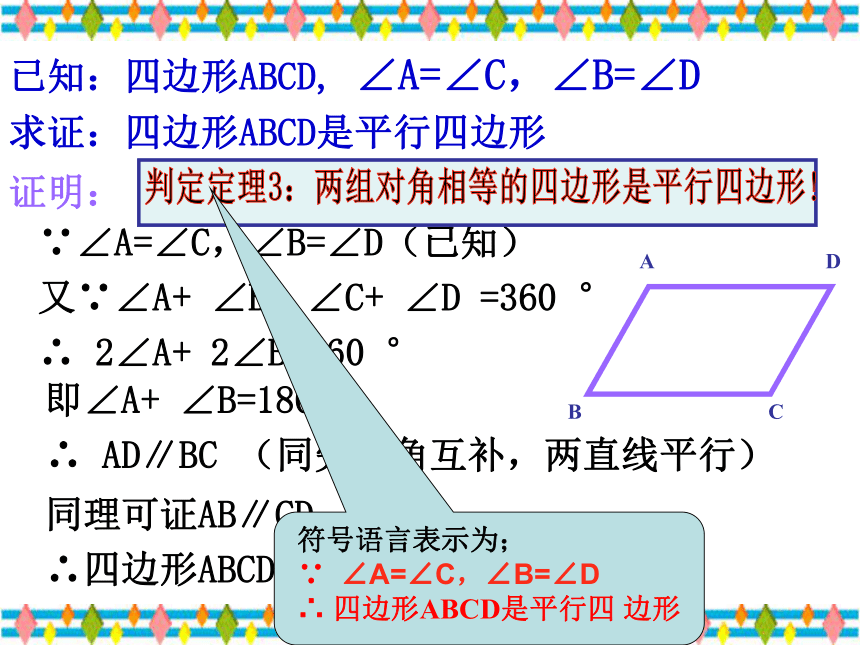
四边形是平行四边形!a平行四边形 对边平行平行四边形 对边相等平行四边形 对角相等平行四边形 邻角互补平行四边形 对角线互相平分定义判定定理1??a判定定理2:一组对边平行且相等的四边形是平行四边形!BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形判定定理3:两组对角相等的四边形是平行四边形!已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
AO = CO
∠1 = ∠2
BO = DO ,∴△AOB≌△COD(SAS)∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4在△AOB和△COD中证明:已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD(SAS)∴AB=CD同理 : AD=CB∴四边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
判定定理4:对角线互相平分的四边形是平行四边形!课堂练习1:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C如图,在 ?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地连出平行四边形。ADCBEFGHO课堂练习2:如图:在平行四边形ABCD中,E、F、G、H分别是各
边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。综合练习1已知:E、F是平行四边形ABCD对角线AC 上的两点,并且AE=CF
求证:四边形BFDE是平行四边形DOABCEF ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
证明:连结BD,交AC于点O综合练习2(寻找最简单的方法)BE∥DF小结:平行四边形的判定方法在四边形ABCD 中,AD∥BC,且AD >BC,BC = 6cm,P,Q 分别从A,C 同时出发,P 以1厘米/秒的速度由A 向D 运动,Q 以2厘米/秒的速度由C 向B 运动,几秒后四边形ABQP 成为平行四边形? 课后探索课后习题 如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F,那么BE=CF,请你说明理由.ABCDEF123
四边形叫做平行四边形.判定定理1:两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形吗?BDAC已知:四边形ABCD, AB=DC,AB∥DC
求证:四边形ABCD是平行四边形新知学习分析:我们目前学了两种方法判定平行四边形,所以本题的证明有两个途径:一个通过定义证,一个通过判定定理1证定义:两组对边分别平行的
四边形叫做平行四边形.判定定理1:两组对边分别相等的四边形是平行四边形。一组对边平行且相等的四边形是平行四边形吗?BDAC已知:四边形ABCD, AB=CD,AB∥DC
求证:四边形ABCD是平行四边形新知学习一组对边平行且相等的四边形是平行四边形吗?
在△ABC和△CDA中 AB=CD
∠1=∠2
AC=AC ∴△ABC≌△CDA(SAS)证明:连结AC,∵ AB∥DC∴∠1=∠212(两直线平行,内错角相等)∴∠BCA=∠DAC(两组对边分别平行的四边
形是平行四边形)∴AD∥BC∴四边形ABCD是平行四边形(全等三角形的对应角相等)(内错角相等,两直线平行)∴BC=DA(两组对边分别相等的四边
形是平行四边形)∵AB=CD,BC=DA∴四边形ABCD是平行四边形(全等三角形的对应边相等)判定定理2:一组对边平行且相等的四边形是平行四边形!符号语言表示为; ∵AB∥CD,AB=CD
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形。) 下列哪些四边形是平行四边形?为什么?还有其它的判定方法吗?判定定理2:一组对边平行且相等的
四边形是平行四边形!a平行四边形 对边平行平行四边形 对边相等平行四边形 对角相等平行四边形 邻角互补平行四边形 对角线互相平分定义判定定理1??a判定定理2:一组对边平行且相等的四边形是平行四边形!BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °证明:即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形判定定理3:两组对角相等的四边形是平行四边形!已知:四边形ABCD, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形
AO = CO
∠1 = ∠2
BO = DO ,∴△AOB≌△COD(SAS)∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)∴ ∠3 = ∠4在△AOB和△COD中证明:已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证明:在△AOB和△COD中∴ △AOB ≌ △COD(SAS)∴AB=CD同理 : AD=CB∴四边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
判定定理4:对角线互相平分的四边形是平行四边形!课堂练习1:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C如图,在 ?ABCD中,已知两条对角线相交于点O,E、F、G、H分别是AO、BO、CO、DO的中点,
以图中的点为顶点,尽可能多地连出平行四边形。ADCBEFGHO课堂练习2:如图:在平行四边形ABCD中,E、F、G、H分别是各
边上的点,且AE=CF,BG=DH。求证:EF与GH互相平分。综合练习1已知:E、F是平行四边形ABCD对角线AC 上的两点,并且AE=CF
求证:四边形BFDE是平行四边形DOABCEF ∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又∵ BO=DO
∴ 四边形BFDE是平行四边形
证明:连结BD,交AC于点O综合练习2(寻找最简单的方法)BE∥DF小结:平行四边形的判定方法在四边形ABCD 中,AD∥BC,且AD >BC,BC = 6cm,P,Q 分别从A,C 同时出发,P 以1厘米/秒的速度由A 向D 运动,Q 以2厘米/秒的速度由C 向B 运动,几秒后四边形ABQP 成为平行四边形? 课后探索课后习题 如图,在△ABC中,BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F,那么BE=CF,请你说明理由.ABCDEF123
