人教版小学五年级数学下册第三单元长方体和正方体同步练习(含答案)
文档属性
| 名称 | 人教版小学五年级数学下册第三单元长方体和正方体同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览




文档简介
1.长方体和正方体的认识
第1课时 长方体
1.看右面的图填空。
(1)这个长方体有( )个面,每个面都是( )形,有( )条长、( )条宽、( )条高。
(2)这个长方体的长是( )dm、宽是( )dm、高是( )dm。
(3)沿这个长方体的所有棱粘一圈胶带,至少需要( )dm的胶带。
2.选一选。
(1)一个长方体,最多有( )条棱长度相等。
A.2 B. 4 C.8
(2)用一根长48cm的钢管,可以焊接成一个长7cm,宽2cm,高( )cm的长方体框架。
A.3 B.4 C.5
(3)下列说法中,不正确的是( )。
A.有6个面,8个顶点,12条棱的图形一定是长方体
B.在一个长方体中,与一条长平行的棱有3条,与一条宽相交并垂直的棱有4条
C.如果一个长方体有四个面完全相同,则其余两个面一定是正方形
3.在下图中找出6个面,使它们能组成一个长方体,这6个面的编号分别是( )。
4.用一根彩带捆扎一个礼盒(如图)。已知接头处的彩带长26cm,这根彩带一共长多少厘米?
5.用一根28cm长的铁丝做一个长、宽、高都是整厘米数的长方体框架,这个长方体框架的长、宽、高可能是多少厘米?想一想,填一填。(长、宽、高3个数据相同的为同一组,如1,2,3和2,1,3)
第2课时 正方体
1.下面图形中,哪些是正方体?(在符合条件的括号里画“√”)
2.判断。
(1)长方体和正方体都有6个面、12条棱、8个顶点。 ( )
(2)有6个面、12条棱、8个顶点的物体不是长方体就是正方体。 ( )
(3)正方体是特殊的长方体。 ( )
(4)一张正方形的纸是一个正方体。 ( )
3.填空。
(1)一个正方体的棱长总和是36cm,它的一个面的面积是( )cm2。
(2)制作4个棱长为6dm的正方体铁框,至少需要( )dm长的铁丝。
(3)把一个长方体(如右图)切割成一个最大的正方体。如果a>b>c,则这个正方体的棱长总和是( )。
(4)如图所示,小丽已经在一个大正方体盒子中摆了10个相同的小正方体,如果要摆满整个大正方体盒子,还需要( )个这样的小正方体。
4.下面的长方体和正方体都是由棱长为2cm的小正方体搭成的,根据图形填空。
长( )cm 宽( )cm
棱长( )cm
高( )cm
棱长总和( )cm
棱长总和( )cm
5.如图所示,王叔叔为了美观,要沿着正方体鱼缸的所有棱给鱼缸镶上合金边框。如果鱼缸的棱长是8dm,至少需要多长的合金边框?
6.小明用字母A、B、C、D、E、F标出了一个正方体的各个面。下图是从三个不同方位看到的这个正方体,猜一猜字母A、B,C的对面是什么字母。
2.长方体和正方体的表面积
第1课时 长方体和正方体的表面积(1)
1.想一想,选一选。
(1)下面图形( )折叠后不能围成正方体。
A. B. C.
A.鸡 B.狗 C.猫
2.在右面的长方体展开图上(单位:cm),先分别用“上”“下”“前”“后”“左”“右”标明6个面,再计算前面、左面和上面的面积。
前面的面积是( )cm2,左面的面积是( )cm2,上面的面积是( )cm2。
3.填空。
(1)一个长方体的长是10cm,宽是3cm,高是2cm,它的表面积是( )cm2。
(2)一个正方体的棱长是5dm,它一个面的面积是( )dm2,表面积是( )dm2。
4.一块长30cm,宽25cm的长方形铁皮,从四个角各剪掉一个边长是5cm的正方形,然后做成无盖的盒子。盒子的表面积是多少平方厘米?
5.在一个大正方体上挖去一个棱长是1cm的小正方体,大正方体的表面积发生变化吗?如果发生变化?变化了多少?
表面积( ) 表面积( ) 表面积( )
第2课时 长方体和正方体的表面积(2)
1.先判断给出的物体是正方体还是长方体,再计算表面积。
名称 长/cm 宽/cm 高/cm 表面积/cm2
30 20 20
20 20 20
30 15 20
2.一种长方体铁皮通风管长2m,管口是边长4dm的正方形,做100根这样的通风管,至少需要多少平方米的铁皮?
3.王老师要做一个长60cm,宽40cm,高50cm的无盖长方体玻璃缸,至少需要多少平方米玻璃?
4.一个游泳池长50m、宽40m、深2m,在池子的四壁和底部涂上水泥,如果每平方米需水泥10千克,一共需要多少千克的水泥?
5.有一个用金属制作而成的机器零件,形状和数字“0”相似(如图,单位:dm)。它的表面积是多少平方分米?
6.如右图,用3个完全相同的小正方体拼成一个长方体后,表面积减少了100dm2,原来每个小正方体的表面积是多少平方分米?长方体的表面积是多少平方分米?
3.长方体和正方体的体积
第1课时 体积和体积单位
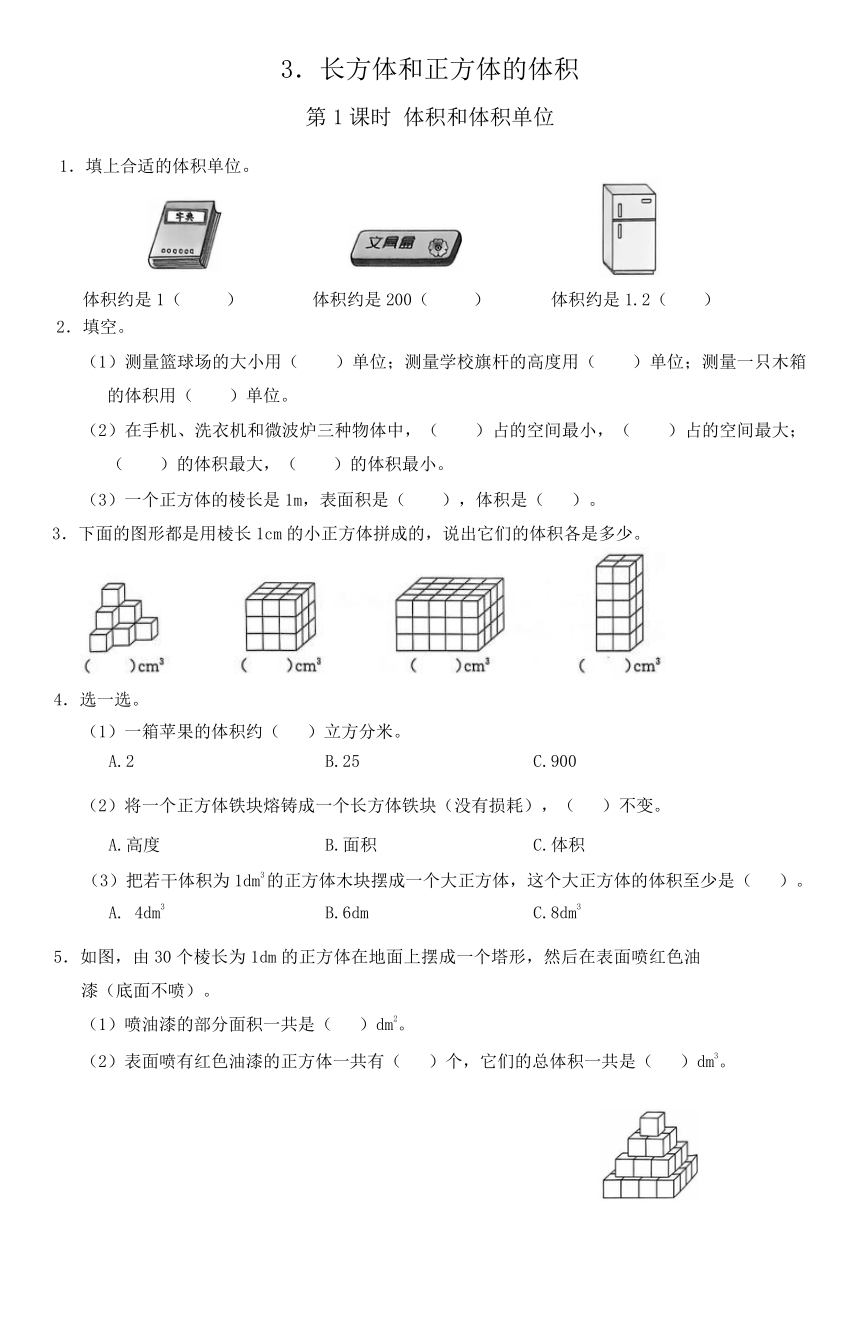
1.填上合适的体积单位。
体积约是1( ) 体积约是200( ) 体积约是1.2( )
2.填空。
(1)测量篮球场的大小用( )单位;测量学校旗杆的高度用( )单位;测量一只木箱的体积用( )单位。
(2)在手机、洗衣机和微波炉三种物体中,( )占的空间最小,( )占的空间最大;( )的体积最大,( )的体积最小。
(3)一个正方体的棱长是1m,表面积是( ),体积是( )。
3.下面的图形都是用棱长1cm的小正方体拼成的,说出它们的体积各是多少。
4.选一选。
(1)一箱苹果的体积约( )立方分米。
A.2 B.25 C.900
(2)将一个正方体铁块熔铸成一个长方体铁块(没有损耗),( )不变。
A.高度 B.面积 C.体积
(3)把若干体积为1dm3的正方体木块摆成一个大正方体,这个大正方体的体积至少是( )。
A. 4dm3 B.6dm C.8dm3
5.如图,由30个棱长为1dm的正方体在地面上摆成一个塔形,然后在表面喷红色油漆(底面不喷)。
(1)喷油漆的部分面积一共是( )dm2。
(2)表面喷有红色油漆的正方体一共有( )个,它们的总体积一共是( )dm3。
第2课时 长方体和正方体的体积(1)
1.计算下面立体图形的体积。(单位:cm)
2.填空。
(1)一个长方体,长是2m,宽和高都比长少0.2m。它的体积是( )m3。
(2)一个长方体的底面积是108cm2,高是8cm,它的体积是( )cm3。
(3)一块正方体石料,一个面的面积是64dm2。这块石料的体积是( )dm3。
(4)有一块棱长是8dm的正方体铁块,现在要把它熔铸成一个横截面面积是20dm2的长方体,这个长方体的长是( )dm。
3.三峡泄洪坝共有23个泄洪孔,每个泄洪孔的宽是21m,高是126m。泄洪时,通过泄洪孔的水流速度是1.8米/秒。每个泄洪孔1分钟能泄洪多少立方米?
4.将一根长5.2m的长方体木料锯成两段后,表面积增加了0.48m2。这根木料原来的体积是多少立方米?
5.将一个长方体的高减小10cm,变成了正方体,正方体表面积比原来长方体表面积减少了320cm2。原来长方体的体积是多少立方厘米?
第3课时 长方体和正方体的体积(2)
1.填出下表中长方体或正方体的相关数据。
名称 底面积 高 体积
长方体 32cm2 ( )cm 224cm3
长方体 50cm2 5dm ( )cm3
正方休 棱长9m ( )m3
2.填空。
(1)学校操场上填平的沙坑里有4方的沙子,已知沙坑长2.5m,宽2m,则沙坑深( )m。
(2)一个正方体的棱长总和是24dm,它的表面积是( )dm2,体积是( )dm3。
(3)一个长方体的长、宽、高分别是am、bm、hm。如果高增加2m,体积比原来增加( )m3。
3.一张正方形硬皮纸,边长是24cm。从四个角各剪掉一个边长为4cm的正方形(如图),然后做成一个无盖的长方体盒子。
(1)如果要给这个无盖的盒子补上一个盖子,则这个盖子至少需要( )cm2的硬皮纸。
(2)有盖长方体盒子的体积是多少立方厘米?
4.一节采煤车厢里面长3m,宽1.5m。车厢内装载的煤高1m。如果每立方米煤重1.33吨,这节采煤车厢装载的煤大约有多少吨?(精确到0.01)
5.将棱长16dm的正方体铁块熔铸成长10dm、宽8dm的长方体。长方体的高是多少分米?
6.有一个长方体,底面是正方形,高是16cm,侧面展开是一个长方形,长是宽的2倍。这个长方体的体积是多少立方厘米?
要点巩固练习1
1.看图连一连。
2.计算下面图形的表面积和体积。
3.根据表格填空。
图形 长 宽 高 棱长总和 表面积 体积
长方体 8cm 3cm 64cm
正方体 84m
长方体 12dm 6dm 9dm
4.计算下面图形的表面积和体积。
第4课时 体积单位间的进率
1.在下面的( )里填上适当的数。
2.比较大小。
3.划去每组数据中与其他数据不相等的那个数。
4.一种煤气灶包装箱是长方体,高2dm,长是高的4倍,宽50cm。100个这样的包装箱的体积是多少立方米?
5.修一条长2000m、宽20m的公路,要先铺1dm厚的三合土,再铺0.6dm厚的沙石,需要三合土和沙石共多少立方分米?合多少立方米?
6.一个长方体的长为3dm,高为15cm,前后两个面、上面和右侧面的面积之和是1800cm2。这个长方体的体积是多少立方分米?
第5课时 容积和容积单位广场
1.填上适当的容积单位。
3.填空。
(1)据有关资料显示,一个儿童每天大约需要喝水1100mL,相当于( )L。照此计算,1个月(按30天计算)大约喝水( )L。
(2)一个长方体玻璃鱼缸,从里面量长0.4m,宽2.4dm,高3dm,它的容积是( )L。
(3)一种口服液每瓶10mL,装350瓶需要口服液( )L;现有口服液7L,可以( )瓶。
4.一个正方体水箱里面的底面周长是4m,装入320L水,水箱内的水有多高?
5.从里面量某汽车油箱的长、宽、高如图所示(单位:cm)。如果每升汽油重0.73kg,这个油箱能装多少千克汽油?
6.一块长22dm的长方形铁皮(厚度不计),四个角各剪去边长为5dm的正方形,焊成一个无盖长方体铁皮盒。这个铁皮盒可以盛水480L,原来长方形铁皮的面积是多少?
第6课时 不规则物体的体积广场
1.填空。
(1)右图中这块石头的体积是( )cm3。
(2)将8个西红柿浸没在盛了250mL水的量杯中,水位上升至950mL,平均每个西红柿的体积是( )cm3。
(3)在一个底面积为20cm2的长方体水箱里,浸没了一块体积是48cm3的石块,如果取出石块,水面会下降( )cm。
2.右图是丁丁测量一个土豆体积时做的实验,请问丁丁用来实验的这个土豆的体积是多少立方厘米?(单位:cm)
3.小海家有一个正方体的鱼缸,从里面量棱长是30cm,鱼缸里养着一些漂亮的金鱼,此时水面高20cm。当取出10条金鱼后水面下降1mm,平均每条金鱼的体积是多少立方厘米?
4.一个长方体的玻璃缸,从里面量长20cm,宽15cm,高10cm。缸里的水深8cm,将一块石头放人缸里完全浸没,溢出了100mL的水,这块石头的体积是多少立方厘米?
5.一个无水的鱼缸,从里面量长0.6m,宽40cm,高50cm。里面放有一块高为24cm、体积为3600cm3的假山石,如果以每分钟9dm3的流速向鱼缸内注水,那么至少需要多长时间能将假山石完全淹没?
整理和复习(1)
1. 3200mL=( )L 2.6立方分米=( )升=( )毫升
0.9L=( )mL 1500毫升=( )升=( )立方分米
5600cm3=( )L 0.8升=( )立方分米=( )立方厘米
2.在( )里填上合适的体积或容积单位。
(1)一个墨水瓶的容积约是60( )。 (2)一个火柴盒的体积约是12( )。
(3)一台冰箱的容积约是230( )。 (4)一箱梨的体积约是20( )。
(5)一个矿泉水瓶的容积约是550( )。 (6)某仓库的容积约是180( )。
3.下列图形中,折叠后能围成正方体的画“√”。
4.用一根长7.2m的铁丝做一个尽可能大的长方体框架(如图)。
(1)这个框架的高是( )dm。
(2)如果在它的表面糊纸做成一个长方体纸箱,至少要用纸( )㎡。
(3)这个长方体纸箱的体积是( )dm3。
5.有一块长10cm、宽2cm、高7cm的长方体木块,在它的左右两角各切掉一块棱长是2cm的小正方体后做成一个模具。这个模具的表面积是多少?体积是多少?
6.右图是一个棱长为8cm的正方体,分别在前面、右面、上面三个面的中心挖去一个棱长是2cm的小正方体做成一种模型。这个模型的表面积和体积各是多少?
整理和复习(2)
1.填表。
图形名称 长 宽 高 底面积 表面积 休积
长方体 10cm 10cm 8cm
8m 6m 480m3
正方体 16dm2
2.选择。
(1)长方体的长、宽、高分别扩大到原来的2倍,这个长方体的体积就扩大到原来的( )倍。
A.2 B.4 C.8
(2)一个包装盒,如果从里面量长28cm,宽20cm,体积为8.4dm3。爸爸想用它包装一件长25cm,宽16cm,高18cm的玻璃器皿,( )装下。
A.能 B.不能 C.无法确定能否
(3)李大伯家要挖一个长50dm、宽25dm、深20dm的水池,如果每立方米土重1.5吨。挖这个水池挖出来的土重( )吨。
A. 37500 B.2500 C.37.5
3.在一个长30cm、宽18cm、高20cm的长方体玻璃缸中装入一个红薯,然后往缸中注一些水,使红薯完全淹没,这时水深15cm。当红薯从水中取出时,缸中的水深13cm。红薯的体积是多少立方分米?
4.一部电梯,从里面量长135cm,宽140cm,高240cm。如果每人乘电梯时的占地面积是18dm2,所占空间是270dm3,那么这部电梯最多能乘多少人?(不考虑限重)
5.有甲、乙两个水箱,从里面测量的数据如右图(单位:cm)。甲水箱装满水,乙水箱空着。现将甲水箱里的一部分水抽到乙水箱中,使两水箱水面高度一样。两个水箱的水面高度是多少厘米?
探索图形
1.看图填一填。
(1)右图中的正方体分别是用几个小正方体拼成的?
A用( )个;B用( )个;
C用( )个;D用( )个。
(2)如果把它们的表面分别涂上颜色,A、B、C、D中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
编号 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
A
B
C
D
(3)按这样的规律摆下去,编号为E、F的正方体的结果会是怎样的?
编号 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
E
F
(4)如果用n表示正方体的棱长(所含小正方体的块数),规律可以表示如下:
①三面涂色的小正方体,位置在各顶点,块数= 。
②两面涂色的小正方体,位置在各条棱上,块数= 。
③一面涂色的小正方体,位置在各个面中间,块数= 。
④没有涂色的小正方体,位置在最外层正方体里面,块数= 。
2.在一个正方体木块的6个面涂上红色后,把它分割成若干个棱长是1cm的小正方体木块,如果两面涂红色的共108个,那么只有一面涂红色的有多少个?
3.如图,这是一个用若干块大小相同的小正方体粘成的模型。把这个模型的表面(包括底面)都涂成红色,那么把这个模型拆开以后,六面都涂上红色的有( )块,五面涂上红色的有( )块,四面涂上红色的有( )块,三面涂上红色的有( )块,两面涂上红色的有( )块,一面涂上红色的有( )块,没有涂上红色的有( )块。
答案
1.长方体和正方体的认识
第1课时长方体
1.(1)6 长方 4 4 4 (2)3 2 8 (3)52
2.(1)C (2)A (3)A
3.①③④⑤⑥⑦
4.2×12+20×2+8×4+26=122(cm)
5.(1)1 2 4 (2)1 3 3 (3)1 1 5 (4)2 2 3
第2课时 正方体
2.(1)√ (2)× (3)√ (4)×
3.(1)9 (2)288 (3)12c (4)54
4.8 4 4 64 6 72
5.8×12=96(dm)
6.A的对面是E,B的对面是F,C的对面是D。
2.长方体和正方体的表面积
第1课时 长方体和正方体的表面积(1)
1.(1)C (2)A B C
2.图略 45 36 180
3.(1)112 (2)25 150
4.盒子的表面积是650cm2
5.不变 增加2cm2 增加4cm2
第2课时 长方体和正方体的表面积(2)
1.长方体 3200 正方体 2400 长方体 2700
2.4dm=0.4m 0.4×2×4×100=320(m2)
3.至少需要1.24㎡玻璃。
4.
2360×10=23600(千克)
5.(6×2+6×10+2×10)×2-4×8×2+2×8×2+4×2×2=168(dm2)
6.3个小正方体拼成长方体后,减少4个正方形的面,所以一个正方形的面积为100÷4=25(dm2)
小正方体的表面积:25×6=150(dm2)
长方体表面积:
3.长方体和正方体的体积
第1课时体积和体积单位
1.dm3 cm3 m3
2.(1)面积 长度 体积
(2)手机 洗衣机 洗衣机 手机 (3)6m2 1m3
3.10 27 60 20
4.(1)B (2)C (3)C
5.(1)56 (2)25 25
提示:喷油漆的部分应该是四周加上上面的面积。上面面积:4×4=16(dm2);
四周面积:(1×4+1×3+1×2+1×1)×4=40(dm2);面积总和:40+16=56(dm2)
第2课时 长方体和正方体的体积(1)
2.(1)6.48 (2)864 (3)512 (4)25.6
3.1分钟=60秒 21×126×1.8×60=285768(m3)
80÷10=8(cm)
第3课时 长方体和正方体的体积(2)
1.7 2500 729
2.(1)0.8 (2)24 8 (3)2ab
3.(1)256 (2)(24-4×2)×(24-4×2)×4=1024(cm3)
4.3×1.5×1×1.33≈5.99(吨)
5.16×16×16÷(10×8)=51.2(dm)
6.侧面展开后的长方形的长:16×2=32(cm)
长方体的底面边长::32÷4=8(cm)
体积:8×8×16=1024(cm3)
要点巩固练习1
2.表面积:
体积:
体积:
体积:
体积:
第4课时 体积单位间的进率
1.400 3500 250 0.36 1.42 60000
2.< = < > = <
3.(1)划去:30500cm3 (2)划去:0.07024m3
4.(2×4)×5×2=80(dm3)=0.08(m3)
5.需要三合土和沙石共6400000dm3,合6400m3。
6.上面和右侧面的面积和是:
宽:900÷(30+15)=20(cm)
体积:
第5课时 容积和容积单位
1.mL L L mL
3.(1)1.1 33 (2)28.8 (3)3.5 700
4.4m=40dm 40÷4=0(dm)
320÷(10×10)=3.2(dm)
5.
192×0.73=140.16(kg)
铁皮盒底面长:22-5×2=12(dm)
铁皮盒底面宽:480÷5÷12=8(dm)
铁皮原来的宽:8+5×2=18(dm)
原来长方形铁皮的面积:
第6课时 不规则物体的体积
1.(1)17 (2)87.5 (3)2.4
2.9.5-8=1.5(cm)
3.1mm=0.1cm 30×30×0.1=90(cm3) 90÷10=9(cm3)
4.
5.
54÷9=6(分钟)
整理和复习(1)
1.3.2 2.6 2600 900 1.5 1.5 5.6 0.8 800
2.(1)mL (2)cm3 (3)L (4)dm3 (5)mL (6)m3
4.(1)4 (2)2.08 (3)192
6.表面积:
体积:
整理和复习(2)
2.(1)C (2)B (3)C
3.30×18×(15-13)=1080(cm3)=1.08(dm3)
4.这部电梯最多能乘10人。
5.甲水箱的体积:30×20×16=9600(cm3)
9600÷(30×20+20×20)=9.6(cm)
探索图形
2.正方体的棱长:108÷12+2=11(cm) 只有一面涂红色:(11-2)2×6=486(个)
3. 0 1 4 28 16 25 10
第1课时 长方体
1.看右面的图填空。
(1)这个长方体有( )个面,每个面都是( )形,有( )条长、( )条宽、( )条高。
(2)这个长方体的长是( )dm、宽是( )dm、高是( )dm。
(3)沿这个长方体的所有棱粘一圈胶带,至少需要( )dm的胶带。
2.选一选。
(1)一个长方体,最多有( )条棱长度相等。
A.2 B. 4 C.8
(2)用一根长48cm的钢管,可以焊接成一个长7cm,宽2cm,高( )cm的长方体框架。
A.3 B.4 C.5
(3)下列说法中,不正确的是( )。
A.有6个面,8个顶点,12条棱的图形一定是长方体
B.在一个长方体中,与一条长平行的棱有3条,与一条宽相交并垂直的棱有4条
C.如果一个长方体有四个面完全相同,则其余两个面一定是正方形
3.在下图中找出6个面,使它们能组成一个长方体,这6个面的编号分别是( )。
4.用一根彩带捆扎一个礼盒(如图)。已知接头处的彩带长26cm,这根彩带一共长多少厘米?
5.用一根28cm长的铁丝做一个长、宽、高都是整厘米数的长方体框架,这个长方体框架的长、宽、高可能是多少厘米?想一想,填一填。(长、宽、高3个数据相同的为同一组,如1,2,3和2,1,3)
第2课时 正方体
1.下面图形中,哪些是正方体?(在符合条件的括号里画“√”)
2.判断。
(1)长方体和正方体都有6个面、12条棱、8个顶点。 ( )
(2)有6个面、12条棱、8个顶点的物体不是长方体就是正方体。 ( )
(3)正方体是特殊的长方体。 ( )
(4)一张正方形的纸是一个正方体。 ( )
3.填空。
(1)一个正方体的棱长总和是36cm,它的一个面的面积是( )cm2。
(2)制作4个棱长为6dm的正方体铁框,至少需要( )dm长的铁丝。
(3)把一个长方体(如右图)切割成一个最大的正方体。如果a>b>c,则这个正方体的棱长总和是( )。
(4)如图所示,小丽已经在一个大正方体盒子中摆了10个相同的小正方体,如果要摆满整个大正方体盒子,还需要( )个这样的小正方体。
4.下面的长方体和正方体都是由棱长为2cm的小正方体搭成的,根据图形填空。
长( )cm 宽( )cm
棱长( )cm
高( )cm
棱长总和( )cm
棱长总和( )cm
5.如图所示,王叔叔为了美观,要沿着正方体鱼缸的所有棱给鱼缸镶上合金边框。如果鱼缸的棱长是8dm,至少需要多长的合金边框?
6.小明用字母A、B、C、D、E、F标出了一个正方体的各个面。下图是从三个不同方位看到的这个正方体,猜一猜字母A、B,C的对面是什么字母。
2.长方体和正方体的表面积
第1课时 长方体和正方体的表面积(1)
1.想一想,选一选。
(1)下面图形( )折叠后不能围成正方体。
A. B. C.
A.鸡 B.狗 C.猫
2.在右面的长方体展开图上(单位:cm),先分别用“上”“下”“前”“后”“左”“右”标明6个面,再计算前面、左面和上面的面积。
前面的面积是( )cm2,左面的面积是( )cm2,上面的面积是( )cm2。
3.填空。
(1)一个长方体的长是10cm,宽是3cm,高是2cm,它的表面积是( )cm2。
(2)一个正方体的棱长是5dm,它一个面的面积是( )dm2,表面积是( )dm2。
4.一块长30cm,宽25cm的长方形铁皮,从四个角各剪掉一个边长是5cm的正方形,然后做成无盖的盒子。盒子的表面积是多少平方厘米?
5.在一个大正方体上挖去一个棱长是1cm的小正方体,大正方体的表面积发生变化吗?如果发生变化?变化了多少?
表面积( ) 表面积( ) 表面积( )
第2课时 长方体和正方体的表面积(2)
1.先判断给出的物体是正方体还是长方体,再计算表面积。
名称 长/cm 宽/cm 高/cm 表面积/cm2
30 20 20
20 20 20
30 15 20
2.一种长方体铁皮通风管长2m,管口是边长4dm的正方形,做100根这样的通风管,至少需要多少平方米的铁皮?
3.王老师要做一个长60cm,宽40cm,高50cm的无盖长方体玻璃缸,至少需要多少平方米玻璃?
4.一个游泳池长50m、宽40m、深2m,在池子的四壁和底部涂上水泥,如果每平方米需水泥10千克,一共需要多少千克的水泥?
5.有一个用金属制作而成的机器零件,形状和数字“0”相似(如图,单位:dm)。它的表面积是多少平方分米?
6.如右图,用3个完全相同的小正方体拼成一个长方体后,表面积减少了100dm2,原来每个小正方体的表面积是多少平方分米?长方体的表面积是多少平方分米?
3.长方体和正方体的体积
第1课时 体积和体积单位
1.填上合适的体积单位。
体积约是1( ) 体积约是200( ) 体积约是1.2( )
2.填空。
(1)测量篮球场的大小用( )单位;测量学校旗杆的高度用( )单位;测量一只木箱的体积用( )单位。
(2)在手机、洗衣机和微波炉三种物体中,( )占的空间最小,( )占的空间最大;( )的体积最大,( )的体积最小。
(3)一个正方体的棱长是1m,表面积是( ),体积是( )。
3.下面的图形都是用棱长1cm的小正方体拼成的,说出它们的体积各是多少。
4.选一选。
(1)一箱苹果的体积约( )立方分米。
A.2 B.25 C.900
(2)将一个正方体铁块熔铸成一个长方体铁块(没有损耗),( )不变。
A.高度 B.面积 C.体积
(3)把若干体积为1dm3的正方体木块摆成一个大正方体,这个大正方体的体积至少是( )。
A. 4dm3 B.6dm C.8dm3
5.如图,由30个棱长为1dm的正方体在地面上摆成一个塔形,然后在表面喷红色油漆(底面不喷)。
(1)喷油漆的部分面积一共是( )dm2。
(2)表面喷有红色油漆的正方体一共有( )个,它们的总体积一共是( )dm3。
第2课时 长方体和正方体的体积(1)
1.计算下面立体图形的体积。(单位:cm)
2.填空。
(1)一个长方体,长是2m,宽和高都比长少0.2m。它的体积是( )m3。
(2)一个长方体的底面积是108cm2,高是8cm,它的体积是( )cm3。
(3)一块正方体石料,一个面的面积是64dm2。这块石料的体积是( )dm3。
(4)有一块棱长是8dm的正方体铁块,现在要把它熔铸成一个横截面面积是20dm2的长方体,这个长方体的长是( )dm。
3.三峡泄洪坝共有23个泄洪孔,每个泄洪孔的宽是21m,高是126m。泄洪时,通过泄洪孔的水流速度是1.8米/秒。每个泄洪孔1分钟能泄洪多少立方米?
4.将一根长5.2m的长方体木料锯成两段后,表面积增加了0.48m2。这根木料原来的体积是多少立方米?
5.将一个长方体的高减小10cm,变成了正方体,正方体表面积比原来长方体表面积减少了320cm2。原来长方体的体积是多少立方厘米?
第3课时 长方体和正方体的体积(2)
1.填出下表中长方体或正方体的相关数据。
名称 底面积 高 体积
长方体 32cm2 ( )cm 224cm3
长方体 50cm2 5dm ( )cm3
正方休 棱长9m ( )m3
2.填空。
(1)学校操场上填平的沙坑里有4方的沙子,已知沙坑长2.5m,宽2m,则沙坑深( )m。
(2)一个正方体的棱长总和是24dm,它的表面积是( )dm2,体积是( )dm3。
(3)一个长方体的长、宽、高分别是am、bm、hm。如果高增加2m,体积比原来增加( )m3。
3.一张正方形硬皮纸,边长是24cm。从四个角各剪掉一个边长为4cm的正方形(如图),然后做成一个无盖的长方体盒子。
(1)如果要给这个无盖的盒子补上一个盖子,则这个盖子至少需要( )cm2的硬皮纸。
(2)有盖长方体盒子的体积是多少立方厘米?
4.一节采煤车厢里面长3m,宽1.5m。车厢内装载的煤高1m。如果每立方米煤重1.33吨,这节采煤车厢装载的煤大约有多少吨?(精确到0.01)
5.将棱长16dm的正方体铁块熔铸成长10dm、宽8dm的长方体。长方体的高是多少分米?
6.有一个长方体,底面是正方形,高是16cm,侧面展开是一个长方形,长是宽的2倍。这个长方体的体积是多少立方厘米?
要点巩固练习1
1.看图连一连。
2.计算下面图形的表面积和体积。
3.根据表格填空。
图形 长 宽 高 棱长总和 表面积 体积
长方体 8cm 3cm 64cm
正方体 84m
长方体 12dm 6dm 9dm
4.计算下面图形的表面积和体积。
第4课时 体积单位间的进率
1.在下面的( )里填上适当的数。
2.比较大小。
3.划去每组数据中与其他数据不相等的那个数。
4.一种煤气灶包装箱是长方体,高2dm,长是高的4倍,宽50cm。100个这样的包装箱的体积是多少立方米?
5.修一条长2000m、宽20m的公路,要先铺1dm厚的三合土,再铺0.6dm厚的沙石,需要三合土和沙石共多少立方分米?合多少立方米?
6.一个长方体的长为3dm,高为15cm,前后两个面、上面和右侧面的面积之和是1800cm2。这个长方体的体积是多少立方分米?
第5课时 容积和容积单位广场
1.填上适当的容积单位。
3.填空。
(1)据有关资料显示,一个儿童每天大约需要喝水1100mL,相当于( )L。照此计算,1个月(按30天计算)大约喝水( )L。
(2)一个长方体玻璃鱼缸,从里面量长0.4m,宽2.4dm,高3dm,它的容积是( )L。
(3)一种口服液每瓶10mL,装350瓶需要口服液( )L;现有口服液7L,可以( )瓶。
4.一个正方体水箱里面的底面周长是4m,装入320L水,水箱内的水有多高?
5.从里面量某汽车油箱的长、宽、高如图所示(单位:cm)。如果每升汽油重0.73kg,这个油箱能装多少千克汽油?
6.一块长22dm的长方形铁皮(厚度不计),四个角各剪去边长为5dm的正方形,焊成一个无盖长方体铁皮盒。这个铁皮盒可以盛水480L,原来长方形铁皮的面积是多少?
第6课时 不规则物体的体积广场
1.填空。
(1)右图中这块石头的体积是( )cm3。
(2)将8个西红柿浸没在盛了250mL水的量杯中,水位上升至950mL,平均每个西红柿的体积是( )cm3。
(3)在一个底面积为20cm2的长方体水箱里,浸没了一块体积是48cm3的石块,如果取出石块,水面会下降( )cm。
2.右图是丁丁测量一个土豆体积时做的实验,请问丁丁用来实验的这个土豆的体积是多少立方厘米?(单位:cm)
3.小海家有一个正方体的鱼缸,从里面量棱长是30cm,鱼缸里养着一些漂亮的金鱼,此时水面高20cm。当取出10条金鱼后水面下降1mm,平均每条金鱼的体积是多少立方厘米?
4.一个长方体的玻璃缸,从里面量长20cm,宽15cm,高10cm。缸里的水深8cm,将一块石头放人缸里完全浸没,溢出了100mL的水,这块石头的体积是多少立方厘米?
5.一个无水的鱼缸,从里面量长0.6m,宽40cm,高50cm。里面放有一块高为24cm、体积为3600cm3的假山石,如果以每分钟9dm3的流速向鱼缸内注水,那么至少需要多长时间能将假山石完全淹没?
整理和复习(1)
1. 3200mL=( )L 2.6立方分米=( )升=( )毫升
0.9L=( )mL 1500毫升=( )升=( )立方分米
5600cm3=( )L 0.8升=( )立方分米=( )立方厘米
2.在( )里填上合适的体积或容积单位。
(1)一个墨水瓶的容积约是60( )。 (2)一个火柴盒的体积约是12( )。
(3)一台冰箱的容积约是230( )。 (4)一箱梨的体积约是20( )。
(5)一个矿泉水瓶的容积约是550( )。 (6)某仓库的容积约是180( )。
3.下列图形中,折叠后能围成正方体的画“√”。
4.用一根长7.2m的铁丝做一个尽可能大的长方体框架(如图)。
(1)这个框架的高是( )dm。
(2)如果在它的表面糊纸做成一个长方体纸箱,至少要用纸( )㎡。
(3)这个长方体纸箱的体积是( )dm3。
5.有一块长10cm、宽2cm、高7cm的长方体木块,在它的左右两角各切掉一块棱长是2cm的小正方体后做成一个模具。这个模具的表面积是多少?体积是多少?
6.右图是一个棱长为8cm的正方体,分别在前面、右面、上面三个面的中心挖去一个棱长是2cm的小正方体做成一种模型。这个模型的表面积和体积各是多少?
整理和复习(2)
1.填表。
图形名称 长 宽 高 底面积 表面积 休积
长方体 10cm 10cm 8cm
8m 6m 480m3
正方体 16dm2
2.选择。
(1)长方体的长、宽、高分别扩大到原来的2倍,这个长方体的体积就扩大到原来的( )倍。
A.2 B.4 C.8
(2)一个包装盒,如果从里面量长28cm,宽20cm,体积为8.4dm3。爸爸想用它包装一件长25cm,宽16cm,高18cm的玻璃器皿,( )装下。
A.能 B.不能 C.无法确定能否
(3)李大伯家要挖一个长50dm、宽25dm、深20dm的水池,如果每立方米土重1.5吨。挖这个水池挖出来的土重( )吨。
A. 37500 B.2500 C.37.5
3.在一个长30cm、宽18cm、高20cm的长方体玻璃缸中装入一个红薯,然后往缸中注一些水,使红薯完全淹没,这时水深15cm。当红薯从水中取出时,缸中的水深13cm。红薯的体积是多少立方分米?
4.一部电梯,从里面量长135cm,宽140cm,高240cm。如果每人乘电梯时的占地面积是18dm2,所占空间是270dm3,那么这部电梯最多能乘多少人?(不考虑限重)
5.有甲、乙两个水箱,从里面测量的数据如右图(单位:cm)。甲水箱装满水,乙水箱空着。现将甲水箱里的一部分水抽到乙水箱中,使两水箱水面高度一样。两个水箱的水面高度是多少厘米?
探索图形
1.看图填一填。
(1)右图中的正方体分别是用几个小正方体拼成的?
A用( )个;B用( )个;
C用( )个;D用( )个。
(2)如果把它们的表面分别涂上颜色,A、B、C、D中,三面、两面、一面涂色以及没有涂色的小正方体各有多少块?
编号 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
A
B
C
D
(3)按这样的规律摆下去,编号为E、F的正方体的结果会是怎样的?
编号 三面涂色的块数 两面涂色的块数 一面涂色的块数 没有涂色的块数
E
F
(4)如果用n表示正方体的棱长(所含小正方体的块数),规律可以表示如下:
①三面涂色的小正方体,位置在各顶点,块数= 。
②两面涂色的小正方体,位置在各条棱上,块数= 。
③一面涂色的小正方体,位置在各个面中间,块数= 。
④没有涂色的小正方体,位置在最外层正方体里面,块数= 。
2.在一个正方体木块的6个面涂上红色后,把它分割成若干个棱长是1cm的小正方体木块,如果两面涂红色的共108个,那么只有一面涂红色的有多少个?
3.如图,这是一个用若干块大小相同的小正方体粘成的模型。把这个模型的表面(包括底面)都涂成红色,那么把这个模型拆开以后,六面都涂上红色的有( )块,五面涂上红色的有( )块,四面涂上红色的有( )块,三面涂上红色的有( )块,两面涂上红色的有( )块,一面涂上红色的有( )块,没有涂上红色的有( )块。
答案
1.长方体和正方体的认识
第1课时长方体
1.(1)6 长方 4 4 4 (2)3 2 8 (3)52
2.(1)C (2)A (3)A
3.①③④⑤⑥⑦
4.2×12+20×2+8×4+26=122(cm)
5.(1)1 2 4 (2)1 3 3 (3)1 1 5 (4)2 2 3
第2课时 正方体
2.(1)√ (2)× (3)√ (4)×
3.(1)9 (2)288 (3)12c (4)54
4.8 4 4 64 6 72
5.8×12=96(dm)
6.A的对面是E,B的对面是F,C的对面是D。
2.长方体和正方体的表面积
第1课时 长方体和正方体的表面积(1)
1.(1)C (2)A B C
2.图略 45 36 180
3.(1)112 (2)25 150
4.盒子的表面积是650cm2
5.不变 增加2cm2 增加4cm2
第2课时 长方体和正方体的表面积(2)
1.长方体 3200 正方体 2400 长方体 2700
2.4dm=0.4m 0.4×2×4×100=320(m2)
3.至少需要1.24㎡玻璃。
4.
2360×10=23600(千克)
5.(6×2+6×10+2×10)×2-4×8×2+2×8×2+4×2×2=168(dm2)
6.3个小正方体拼成长方体后,减少4个正方形的面,所以一个正方形的面积为100÷4=25(dm2)
小正方体的表面积:25×6=150(dm2)
长方体表面积:
3.长方体和正方体的体积
第1课时体积和体积单位
1.dm3 cm3 m3
2.(1)面积 长度 体积
(2)手机 洗衣机 洗衣机 手机 (3)6m2 1m3
3.10 27 60 20
4.(1)B (2)C (3)C
5.(1)56 (2)25 25
提示:喷油漆的部分应该是四周加上上面的面积。上面面积:4×4=16(dm2);
四周面积:(1×4+1×3+1×2+1×1)×4=40(dm2);面积总和:40+16=56(dm2)
第2课时 长方体和正方体的体积(1)
2.(1)6.48 (2)864 (3)512 (4)25.6
3.1分钟=60秒 21×126×1.8×60=285768(m3)
80÷10=8(cm)
第3课时 长方体和正方体的体积(2)
1.7 2500 729
2.(1)0.8 (2)24 8 (3)2ab
3.(1)256 (2)(24-4×2)×(24-4×2)×4=1024(cm3)
4.3×1.5×1×1.33≈5.99(吨)
5.16×16×16÷(10×8)=51.2(dm)
6.侧面展开后的长方形的长:16×2=32(cm)
长方体的底面边长::32÷4=8(cm)
体积:8×8×16=1024(cm3)
要点巩固练习1
2.表面积:
体积:
体积:
体积:
体积:
第4课时 体积单位间的进率
1.400 3500 250 0.36 1.42 60000
2.< = < > = <
3.(1)划去:30500cm3 (2)划去:0.07024m3
4.(2×4)×5×2=80(dm3)=0.08(m3)
5.需要三合土和沙石共6400000dm3,合6400m3。
6.上面和右侧面的面积和是:
宽:900÷(30+15)=20(cm)
体积:
第5课时 容积和容积单位
1.mL L L mL
3.(1)1.1 33 (2)28.8 (3)3.5 700
4.4m=40dm 40÷4=0(dm)
320÷(10×10)=3.2(dm)
5.
192×0.73=140.16(kg)
铁皮盒底面长:22-5×2=12(dm)
铁皮盒底面宽:480÷5÷12=8(dm)
铁皮原来的宽:8+5×2=18(dm)
原来长方形铁皮的面积:
第6课时 不规则物体的体积
1.(1)17 (2)87.5 (3)2.4
2.9.5-8=1.5(cm)
3.1mm=0.1cm 30×30×0.1=90(cm3) 90÷10=9(cm3)
4.
5.
54÷9=6(分钟)
整理和复习(1)
1.3.2 2.6 2600 900 1.5 1.5 5.6 0.8 800
2.(1)mL (2)cm3 (3)L (4)dm3 (5)mL (6)m3
4.(1)4 (2)2.08 (3)192
6.表面积:
体积:
整理和复习(2)
2.(1)C (2)B (3)C
3.30×18×(15-13)=1080(cm3)=1.08(dm3)
4.这部电梯最多能乘10人。
5.甲水箱的体积:30×20×16=9600(cm3)
9600÷(30×20+20×20)=9.6(cm)
探索图形
2.正方体的棱长:108÷12+2=11(cm) 只有一面涂红色:(11-2)2×6=486(个)
3. 0 1 4 28 16 25 10
