人教版小学五年级数学下册第三单元考点集训(含答案)
文档属性
| 名称 | 人教版小学五年级数学下册第三单元考点集训(含答案) | 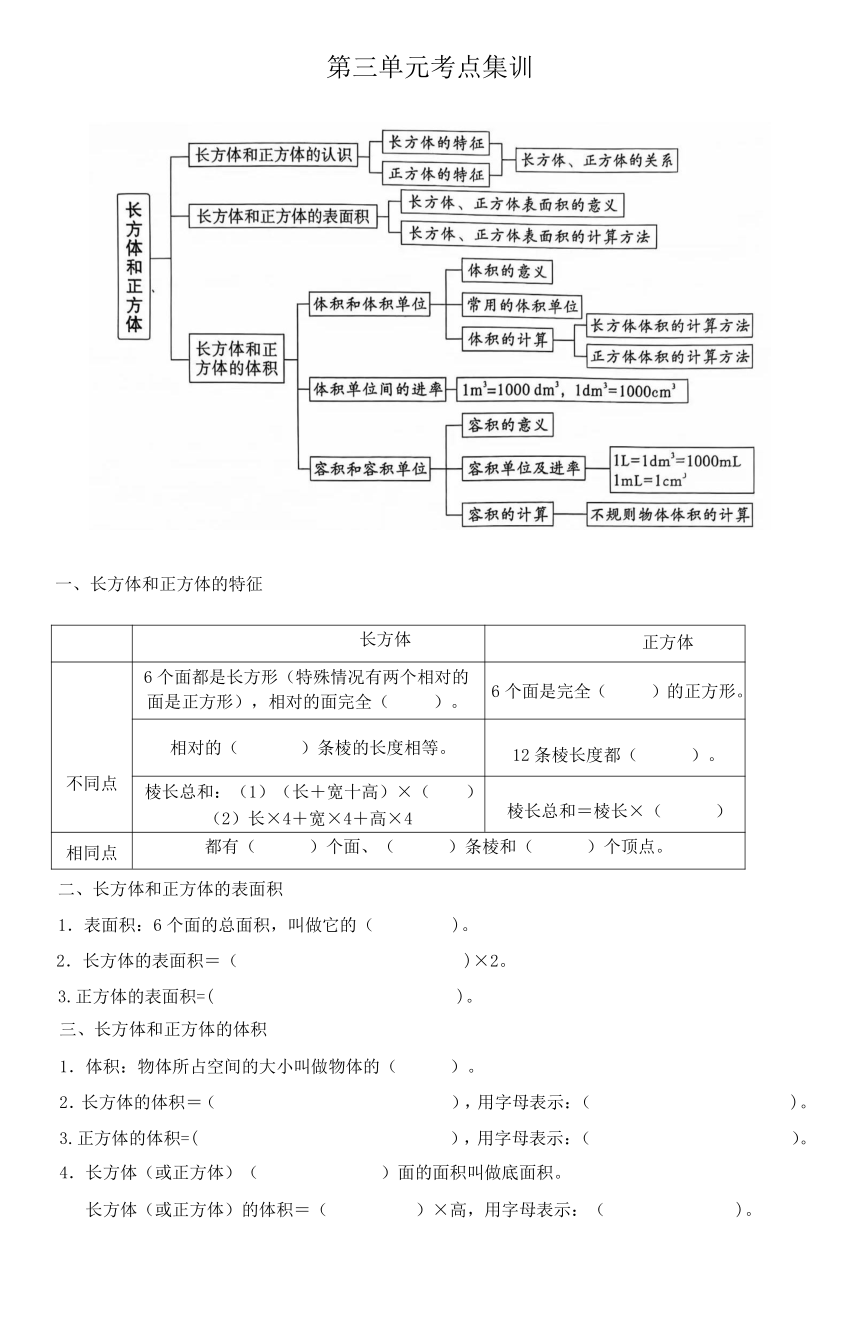 | |
| 格式 | docx | ||
| 文件大小 | 336.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 15:07:32 | ||
图片预览


文档简介
第三单元考点集训
一、长方体和正方体的特征
长方体 正方体
不同点 6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面完全( )。 6个面是完全( )的正方形。
相对的( )条棱的长度相等。 12条棱长度都( )。
棱长总和:(1)(长+宽十高)×( ) (2)长×4+宽×4+高×4 棱长总和=棱长×( )
相同点 都有( )个面、( )条棱和( )个顶点。
二、长方体和正方体的表面积
1.表面积:6个面的总面积,叫做它的( )。
2.长方体的表面积=( )×2。
3.正方体的表面积=( )。
三、长方体和正方体的体积
1.体积:物体所占空间的大小叫做物体的( )。
2.长方体的体积=( ),用字母表示:( )。
3.正方体的体积=( ),用字母表示:( )。
4.长方体(或正方体)( )面的面积叫做底面积。
长方体(或正方体)的体积=( )×高,用字母表示:( )。
四、体积单位、容积和容积单位及进率
1.体积单位间的进率:
2.容积:箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的( )。
3.容积单位及进率:计量容积一般就用( )单位,计量液体的体积,如水、油等,常用( )单位升和毫升,也可以写成L和mL。
1L=( )mL
五、不规则物体的体积
1.形状不规则的物体可以将物体放入盛有水的容器中(水不溢出),通过排水法求体积。
2.排水法的公式:V物体=V现在-V原来
或V物体=S×(h现在-h原来)或V物体=S×h升高。集h训
[考点一]长方体和正方体的认识
1.右面的图形是( )体,长是( )cm,宽是( )cm,高是( )cm,棱长总和是( )cm。把它截成一个最大的正方体,正方体的棱长是( )cm,棱长总和是( )cm。
2.把4个棱长为1cm的正方体拼成一个长方体,有( )种拼法,拼成的长方体的棱长总和分别是( )cm和( )cm。
[考点二]长方体和正方体的表面积及应用
3.选择。
(1)下图中,不能折成正方体的是( )。
(2)从由8个棱长是2cm的小正方体拼成的大正方体中拿走1个小正方体(如右图),这时它的表面积是( )cm2。
A.18 B.24 C.96
4.如右图,用硬纸板做一个礼品盒(单位:dm),并用丝带包扎,丝带接头处长33cm。
(1)至少需要准备( )dm长的丝带。
(2)至少需要用硬纸板多少平方分米?
5.把一个正方体木块,沿棱长切成4个长方体后,表面积增加了24cm2。原来正方体的表面积是( )cm2。
[考点三]长方体和正方体的体积及应用
6.在( )里填上合适的数。
8070mL=( )L
7.填空。
(1)冷藏车车厢的内部长3.5m、宽2.2m、高2m,它的容积是( )m3。
(2)一块长方体形状的大理石,体积为32.4m3,底面是边长为2m的正方形,这块大理石的高是( )m。
(3)一个长方体水池,底面长1.2m,宽6dm.如果要向这个池子里注入2dm高的水,需要( )升水。
(4)将2个梨子浸没在盛了250mL水的量杯后,水位上升至550mL,平均每个梨子的体积是( )cm3。
(5)有三个正方体铁块,它们的表面积分别是96cm2、24cm2、150cm2,现将三个铁块熔成一个大的正方体,这个大正方体的体积是( )cm3
8.一种长方体砖,长0.24m,宽1.2dm,厚6cm。用60000块这样的砖垒成一堵实心墙,这堵墙所占的空间是多少立方米?
9.一个长方体水箱里面长40cm、宽32cm。水箱里装着水,并有一个长20cm、宽16cm的小长方体铁块完全浸没在水中。当把水中的铁块取出后,水面下降了2cm,铁块的高是多少厘米?
10.一个长方体水池,长8m、宽6m、深2.5m,池内水深1.5m,用每分钟抽水4m3的抽水机来注水,多少分钟能把水池注满?
答案
考点梳理
二、1.表面积 2.长×宽+长×高+宽×高
3.棱长×棱长×6
三、1.体积 2.长×宽×高 V=abh
3.棱长×棱长×棱长
4.底 底面积 V=Sh
四、1.1000 1000 2.容积 3.体积 容积 1 1 1000
考点集训
1.长方 10 5 3 72 3 36
2. 2 20 24
3. (1)C (2)C
4.(1)27.3
5. 24
6. 1500 4.75 280 280 8.07 0.312 670 670
7. (1)15.4 (2)8.1 (3)144 (4)150 (5)197
8. 1.2dm=0.12m 6cm=0.06m
0.24×0.12×0.06=0.001728(m3)
0.001728×60000=103.68(㎡)
铁块的体积:40×32×2=2560(cm3)
铁块的高:2560÷20÷16=8(cm)
8×6×(2.5-1.5)÷4=12(分钟)
一、长方体和正方体的特征
长方体 正方体
不同点 6个面都是长方形(特殊情况有两个相对的面是正方形),相对的面完全( )。 6个面是完全( )的正方形。
相对的( )条棱的长度相等。 12条棱长度都( )。
棱长总和:(1)(长+宽十高)×( ) (2)长×4+宽×4+高×4 棱长总和=棱长×( )
相同点 都有( )个面、( )条棱和( )个顶点。
二、长方体和正方体的表面积
1.表面积:6个面的总面积,叫做它的( )。
2.长方体的表面积=( )×2。
3.正方体的表面积=( )。
三、长方体和正方体的体积
1.体积:物体所占空间的大小叫做物体的( )。
2.长方体的体积=( ),用字母表示:( )。
3.正方体的体积=( ),用字母表示:( )。
4.长方体(或正方体)( )面的面积叫做底面积。
长方体(或正方体)的体积=( )×高,用字母表示:( )。
四、体积单位、容积和容积单位及进率
1.体积单位间的进率:
2.容积:箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的( )。
3.容积单位及进率:计量容积一般就用( )单位,计量液体的体积,如水、油等,常用( )单位升和毫升,也可以写成L和mL。
1L=( )mL
五、不规则物体的体积
1.形状不规则的物体可以将物体放入盛有水的容器中(水不溢出),通过排水法求体积。
2.排水法的公式:V物体=V现在-V原来
或V物体=S×(h现在-h原来)或V物体=S×h升高。集h训
[考点一]长方体和正方体的认识
1.右面的图形是( )体,长是( )cm,宽是( )cm,高是( )cm,棱长总和是( )cm。把它截成一个最大的正方体,正方体的棱长是( )cm,棱长总和是( )cm。
2.把4个棱长为1cm的正方体拼成一个长方体,有( )种拼法,拼成的长方体的棱长总和分别是( )cm和( )cm。
[考点二]长方体和正方体的表面积及应用
3.选择。
(1)下图中,不能折成正方体的是( )。
(2)从由8个棱长是2cm的小正方体拼成的大正方体中拿走1个小正方体(如右图),这时它的表面积是( )cm2。
A.18 B.24 C.96
4.如右图,用硬纸板做一个礼品盒(单位:dm),并用丝带包扎,丝带接头处长33cm。
(1)至少需要准备( )dm长的丝带。
(2)至少需要用硬纸板多少平方分米?
5.把一个正方体木块,沿棱长切成4个长方体后,表面积增加了24cm2。原来正方体的表面积是( )cm2。
[考点三]长方体和正方体的体积及应用
6.在( )里填上合适的数。
8070mL=( )L
7.填空。
(1)冷藏车车厢的内部长3.5m、宽2.2m、高2m,它的容积是( )m3。
(2)一块长方体形状的大理石,体积为32.4m3,底面是边长为2m的正方形,这块大理石的高是( )m。
(3)一个长方体水池,底面长1.2m,宽6dm.如果要向这个池子里注入2dm高的水,需要( )升水。
(4)将2个梨子浸没在盛了250mL水的量杯后,水位上升至550mL,平均每个梨子的体积是( )cm3。
(5)有三个正方体铁块,它们的表面积分别是96cm2、24cm2、150cm2,现将三个铁块熔成一个大的正方体,这个大正方体的体积是( )cm3
8.一种长方体砖,长0.24m,宽1.2dm,厚6cm。用60000块这样的砖垒成一堵实心墙,这堵墙所占的空间是多少立方米?
9.一个长方体水箱里面长40cm、宽32cm。水箱里装着水,并有一个长20cm、宽16cm的小长方体铁块完全浸没在水中。当把水中的铁块取出后,水面下降了2cm,铁块的高是多少厘米?
10.一个长方体水池,长8m、宽6m、深2.5m,池内水深1.5m,用每分钟抽水4m3的抽水机来注水,多少分钟能把水池注满?
答案
考点梳理
二、1.表面积 2.长×宽+长×高+宽×高
3.棱长×棱长×6
三、1.体积 2.长×宽×高 V=abh
3.棱长×棱长×棱长
4.底 底面积 V=Sh
四、1.1000 1000 2.容积 3.体积 容积 1 1 1000
考点集训
1.长方 10 5 3 72 3 36
2. 2 20 24
3. (1)C (2)C
4.(1)27.3
5. 24
6. 1500 4.75 280 280 8.07 0.312 670 670
7. (1)15.4 (2)8.1 (3)144 (4)150 (5)197
8. 1.2dm=0.12m 6cm=0.06m
0.24×0.12×0.06=0.001728(m3)
0.001728×60000=103.68(㎡)
铁块的体积:40×32×2=2560(cm3)
铁块的高:2560÷20÷16=8(cm)
8×6×(2.5-1.5)÷4=12(分钟)
