湖南省永州市祁阳市大村甸镇中心学校2024-2025学年下学期期中监测八年级下册数学试卷(含答案)
文档属性
| 名称 | 湖南省永州市祁阳市大村甸镇中心学校2024-2025学年下学期期中监测八年级下册数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 659.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览


文档简介
祁阳市大村甸镇中心学校2024-2025学年下学期期中监测八年级下册《数学》试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列四组线段中,不能构成直角三角形的是( )
A.a=1,,c=2 B.a=1,,c=1
C.a=1,b=2,c=2 D.a=3,b=4,c=5
2.2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标,它( )
A.是轴对称图形 B.是中心对称图形
C.既不是轴对称图形也不是中心对称图形 D.既是轴对称图形又是中心对称图形
第2题图 第3题图 第5题图
3.如图,在菱形ABCD中,E,F分别是AB和BC上的点,添加以下条件仍不能判定△ADE≌△CDF的是( )
A.∠ADE=∠CDF B.∠AED=∠CFD C.DE=DF D.BE=BF
4.在下列条件中,能够判定一个四边形是平行四边形的有( )
①一组对边平行,另一组对边相等②一组对边平行,一条对角线平分另一条对角线
③一组对边平行,一组对角相等④一组对角相等,一条对角线平分另一条对角线
A.1个 B.2个 C.3个 D.4个
5.如图,在 ABCD中,DE平分∠ADC,BC=6,BE=2,则平行四边形ABCD的周长是( )
A.14 B.16 C.20 D.24
6.如图,正方形ABCD,点E为AB边上一点,AE=3,BE=1.∠EDC的平分线交BC于点F,点G是DE的中点,则GF的长为( )
A.2 B.3 C. 2.5 D.3.5
第6题图 第9题图
7.下列四边形中,对角线垂直且相等的是( )
A.菱形B.矩形C.平行四边形 D.正方形
8.在△ABC中,∠C=90°,∠B=2∠A,则∠A=( )
A.15° B.30° C.45° D.60°
9.如图, ABCD中,点O是对角线AC、BD的交点,过点O的直线分别交AD、BC于点M、N,若△CON的面积为3,△DOM的面积为5,则 ABCD的面积是( )
A.16 B.24 C.32 D.40
10.在Rt△ABC中,∠C=90°,且AB=4,若AC=3,那么BC的值是( )
A.1 B.5 C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,在四边形ABCD中,∠A+∠C=180°,∠D=120°,∠ABE是四边形ABCD的一个外角,则∠ABE的度数是 °.
12.如图,EF是△ABC的中位线,BD平分∠ABC,交EF于D,若BC=7,DF=1,则BE= .
第11题图 第12题图 第13 题图
13.如图,∠AOB=30°,OP平分∠AOB,PC∥OB交OA于C.如果OC=6,那么点P到OB的距离等于 .
14.请写出一个是中心对称,但不是轴对称的几何图形名称: .
15.如图,在 ABCD中,AE是∠BAD的平分线,AB=6,AD=4,则CE= .
16.如图,在△ABC中,BD平分∠ABC,BD⊥AD,若∠ACB与∠BAD互补,AC=20,则AD的长为 .
第15题图 第16题图 第18题图
17.三角形三个内角度数之比为1:2:3,若最大边长是6,则最小边长是 .
18.如图,在平面直角坐标系中,依次作点P(﹣3,1)关于直线y=﹣x的对称点P1,P1关于y轴的对称点P2,P2关于x轴的对称点P3,P3关于直线y=﹣x的对称点P4,P4关于y轴的对称点P5,P5关于x轴的对称点P6……按照上述变换规律继续作下去,则点P2025的坐标为 。
三.解答题(共8小题,满分66分)
19.(6分)在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿着到两条公路OM,ON距离相等的一条小路逃窜(如图,在∠MON内),要使埋伏在A,B两处的公安人员在相等的距离同时抓住贩毒分子,请你帮助公安人员在图中标出抓捕点,并简述你的理由.
20.(6分)如图,在△ABE与△CBD中,AE⊥BD于点E,CD⊥BD于点D,AB=BC,BE=CD.证明:Rt△ABE≌Rt△BCD.
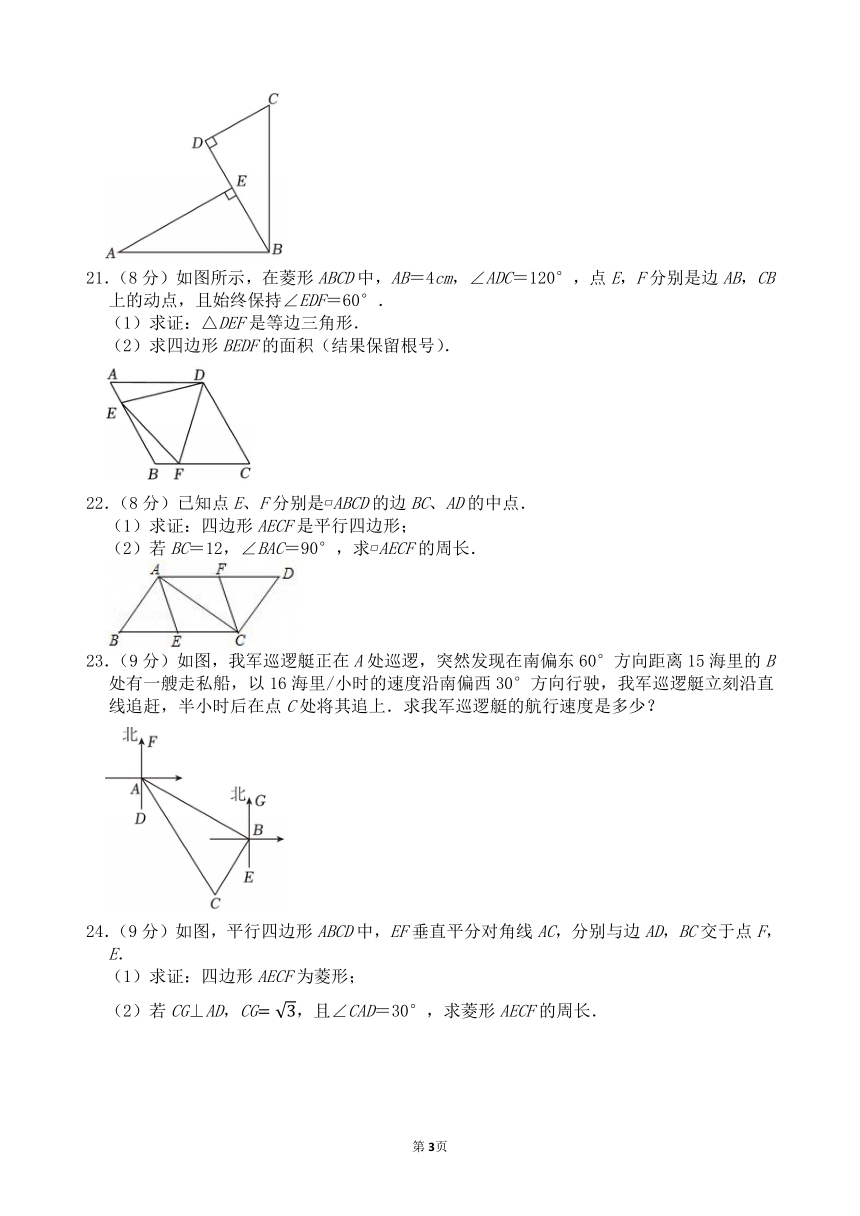
21.(8分)如图所示,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F分别是边AB,CB上的动点,且始终保持∠EDF=60°.
(1)求证:△DEF是等边三角形.
(2)求四边形BEDF的面积(结果保留根号).
22.(8分)已知点E、F分别是 ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=12,∠BAC=90°,求 AECF的周长.
23.(9分)如图,我军巡逻艇正在A处巡逻,突然发现在南偏东60°方向距离15海里的B处有一艘走私船,以16海里/小时的速度沿南偏西30°方向行驶,我军巡逻艇立刻沿直线追赶,半小时后在点C处将其追上.求我军巡逻艇的航行速度是多少?
24.(9分)如图,平行四边形ABCD中,EF垂直平分对角线AC,分别与边AD,BC交于点F,E.
(1)求证:四边形AECF为菱形;
(2)若CG⊥AD,CG,且∠CAD=30°,求菱形AECF的周长.
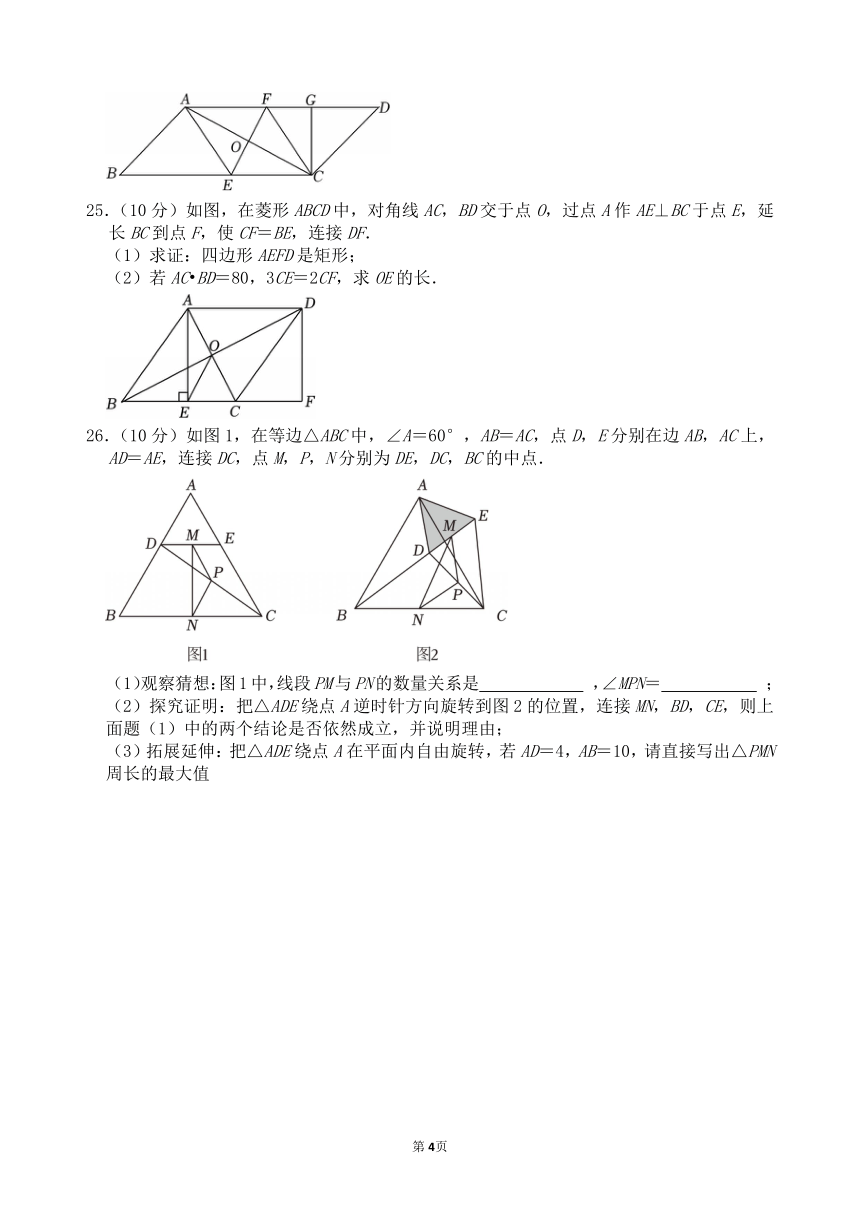
25.(10分)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若AC BD=80,3CE=2CF,求OE的长.
26.(10分)如图1,在等边△ABC中,∠A=60°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:图1中,线段PM与PN的数量关系是 ,∠MPN= ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,则上面题(1)中的两个结论是否依然成立,并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN周长的最大值
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B C C D B C C
11.120.
12..
13.3.
14.平行四边形(答案不唯一).
15.2.
16.10.
17. 3.
18.(1,﹣3)
19.解:如图,作∠MON的平分线OC,连接AB,作线段的垂直平分线与OC交于点P,则点P为抓捕点.
理由:角平分线上的点到角两边的距离相等(即犯罪分子在∠MON的角平分线上,点P也在其上),
线段垂直平分线上的点到线段两端点的距离相等(所以点P在线段AB的垂直平分线上).
∴两线的交点,即点P符合要求.
20.证明:∵AE⊥BD,CD⊥BD,
∴∠AEB=∠BDC=90°,
在Rt△ABE和Rt△BCD中,
,
∴Rt△ABE≌Rt△BCD(HL).
21.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,∠ADC=120°,
∴AB=AD,∠ABC=∠ADC=120°,∠ADB∠ADC=60°,∠DBF∠ABC=60°,
∴△ABD是等边三角形,
∴AD=BD,∠A=∠ADB=60°,
∴∠A=∠DBF,
∵∠EDF=60°,
∴∠ADB﹣∠BDE=∠EDF﹣∠EDB,
即∠ADE=∠BDF,
∴△ADE≌△BDF(ASA),
∴DE=DF,
∴△DEF是等边三角形;
(2)解:如图,过点D作DM⊥AB于点M,
由(1)可知,△ADE≌△BDF,△ABD是等边三角形,
∴四边形BEDF的面积=△ABD的面积,AD=AB=4cm,AMAB=2(cm),
∴DM2(cm),
∴四边形BEDF的面积=△ABD的面积AB DM4×24(cm2).
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是 ABCD的边BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵BC=12,∠BAC=90°,E是BC的中点.
∴AE=CEBC=CE=6,
∴平行四边形AECF是菱形,
∴ AECF的周长=4×6=24.
23.解:如图所示,由题意得,
∠HAB=90°﹣60°=30°,∠MBC=90°﹣∠EBC=60°,
∵AH∥BM,
∴∠ABM=∠BAH=30°,
∴∠ABC=∠ABM+∠MBC=90°,
∵巡逻艇沿直线追赶,半小时后在点C处追上走私船,
∴BC=16×0.5=8(海里),
在Rt△ABC中,∠ABC=90°,AB=15海里,BC=8海里,
∴AC17(海里),
∴我军巡逻艇的航行速度是34(海里/小时).
答:我军巡逻艇的航行速度是34海里/小时.
24.(1)证明:∵EF垂直平分对角线AC,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AD∥BC,
∴四边形AECF是平行四边形,
∵AF=CF,
∴平行四边形AECF为菱形;
(2)解:∵CG⊥AD,
∴∠CGA=90°,
∵∠CAD=30°,
∴AC=2CG=2,
∴AGCG3,
∵四边形AECF是菱形,
∴AE=CE=AF=CF,
设AF=CF=x,则FG=AG﹣AF=3﹣x,
在Rt△CFG中,由勾股定理得:CG2+FG2=CF2,
即()2+(3﹣x)2=x2,
解得:x=2,
∴AF=CF=2,
∴菱形AECF的周长=4AF=8.
25.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∵CF=BE,
∴CF+CE=BE+CE,
即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD是矩形;
(2)解:设CE=2a(a>0),则BE=CF=3a,BC=BE+CE=5a,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∴∠BOC=90°,
∵AE⊥BC,
∴∠AEC=90°,
∴OEAC=OC,
∵cos∠ACE,
∴,
解得:OCa,
∴OB2a,
∵AC BD=80,
∴OA OC=20,
即a 2a=20,
解得:a(负值已舍去),
∴OEa,
即OE的长为.
26.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵AD=AE,
∴AB﹣AD=AC﹣AE,即BD=CE,
∵M,P,N分别是DE,DC,BC的中点,
∴MPEC,PM∥EC,PNBD,PN∥BD,
∴PM=PN,∠MPD=∠ACD,∠NPD=∠ADC,
在△ACD中,∠ADC+∠ACD=180°﹣∠A=120°,
∴∠MPN=∠MPD+∠NPD=120°.
故答案为:PM=PN,120°;
(2)(1)中的两个结论依然成立;理由如下:
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵DM=ME,DP=PC,BN=NC,
∴MPEC,PM∥EC,PNBD,PN∥BD,
∴MP=PN,
∴△PMN是等腰三角形.
∵PM∥CE,
∴∠DPM=∠DCE,
∵PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=60°,
∴∠ACB+∠ABC=120°,
∴∠MPN=120°,
∴PM=PN,∠MPN=120°;
(3)△PMN周长的最大值为14+7;理由如下:
由(2)知:PM=PN,∠MPN=120°,
∵BD≤AB+AD,
∴BD≤14,
∴点D恰好在BA延长线上时,BD、CE取得最大值,且最大值为14,
∴PM、PN的最大值为7,
此时MN经过点A,即MN垂直平分BC,如图,
∵△ABC、△ADE是等边三角形,且AD=4,AB=10,
∴∠BAN=∠DAM=30°,
∴BN=CN=5,DM=EM=2,
∴AN5,AM2,
∴△PMN周长的最大值为PM+PN+MN=7+7+5214+7.
第9页
一.选择题(共10小题,满分30分,每小题3分)
1.下列四组线段中,不能构成直角三角形的是( )
A.a=1,,c=2 B.a=1,,c=1
C.a=1,b=2,c=2 D.a=3,b=4,c=5
2.2024年7月27日,第33届夏季奥运会在法国巴黎举行,如图所示巴黎奥运会项目图标,它( )
A.是轴对称图形 B.是中心对称图形
C.既不是轴对称图形也不是中心对称图形 D.既是轴对称图形又是中心对称图形
第2题图 第3题图 第5题图
3.如图,在菱形ABCD中,E,F分别是AB和BC上的点,添加以下条件仍不能判定△ADE≌△CDF的是( )
A.∠ADE=∠CDF B.∠AED=∠CFD C.DE=DF D.BE=BF
4.在下列条件中,能够判定一个四边形是平行四边形的有( )
①一组对边平行,另一组对边相等②一组对边平行,一条对角线平分另一条对角线
③一组对边平行,一组对角相等④一组对角相等,一条对角线平分另一条对角线
A.1个 B.2个 C.3个 D.4个
5.如图,在 ABCD中,DE平分∠ADC,BC=6,BE=2,则平行四边形ABCD的周长是( )
A.14 B.16 C.20 D.24
6.如图,正方形ABCD,点E为AB边上一点,AE=3,BE=1.∠EDC的平分线交BC于点F,点G是DE的中点,则GF的长为( )
A.2 B.3 C. 2.5 D.3.5
第6题图 第9题图
7.下列四边形中,对角线垂直且相等的是( )
A.菱形B.矩形C.平行四边形 D.正方形
8.在△ABC中,∠C=90°,∠B=2∠A,则∠A=( )
A.15° B.30° C.45° D.60°
9.如图, ABCD中,点O是对角线AC、BD的交点,过点O的直线分别交AD、BC于点M、N,若△CON的面积为3,△DOM的面积为5,则 ABCD的面积是( )
A.16 B.24 C.32 D.40
10.在Rt△ABC中,∠C=90°,且AB=4,若AC=3,那么BC的值是( )
A.1 B.5 C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.如图,在四边形ABCD中,∠A+∠C=180°,∠D=120°,∠ABE是四边形ABCD的一个外角,则∠ABE的度数是 °.
12.如图,EF是△ABC的中位线,BD平分∠ABC,交EF于D,若BC=7,DF=1,则BE= .
第11题图 第12题图 第13 题图
13.如图,∠AOB=30°,OP平分∠AOB,PC∥OB交OA于C.如果OC=6,那么点P到OB的距离等于 .
14.请写出一个是中心对称,但不是轴对称的几何图形名称: .
15.如图,在 ABCD中,AE是∠BAD的平分线,AB=6,AD=4,则CE= .
16.如图,在△ABC中,BD平分∠ABC,BD⊥AD,若∠ACB与∠BAD互补,AC=20,则AD的长为 .
第15题图 第16题图 第18题图
17.三角形三个内角度数之比为1:2:3,若最大边长是6,则最小边长是 .
18.如图,在平面直角坐标系中,依次作点P(﹣3,1)关于直线y=﹣x的对称点P1,P1关于y轴的对称点P2,P2关于x轴的对称点P3,P3关于直线y=﹣x的对称点P4,P4关于y轴的对称点P5,P5关于x轴的对称点P6……按照上述变换规律继续作下去,则点P2025的坐标为 。
三.解答题(共8小题,满分66分)
19.(6分)在一次抓捕贩毒分子的行动中,一贩毒分子从两条公路的交点O处沿着到两条公路OM,ON距离相等的一条小路逃窜(如图,在∠MON内),要使埋伏在A,B两处的公安人员在相等的距离同时抓住贩毒分子,请你帮助公安人员在图中标出抓捕点,并简述你的理由.
20.(6分)如图,在△ABE与△CBD中,AE⊥BD于点E,CD⊥BD于点D,AB=BC,BE=CD.证明:Rt△ABE≌Rt△BCD.
21.(8分)如图所示,在菱形ABCD中,AB=4cm,∠ADC=120°,点E,F分别是边AB,CB上的动点,且始终保持∠EDF=60°.
(1)求证:△DEF是等边三角形.
(2)求四边形BEDF的面积(结果保留根号).
22.(8分)已知点E、F分别是 ABCD的边BC、AD的中点.
(1)求证:四边形AECF是平行四边形;
(2)若BC=12,∠BAC=90°,求 AECF的周长.
23.(9分)如图,我军巡逻艇正在A处巡逻,突然发现在南偏东60°方向距离15海里的B处有一艘走私船,以16海里/小时的速度沿南偏西30°方向行驶,我军巡逻艇立刻沿直线追赶,半小时后在点C处将其追上.求我军巡逻艇的航行速度是多少?
24.(9分)如图,平行四边形ABCD中,EF垂直平分对角线AC,分别与边AD,BC交于点F,E.
(1)求证:四边形AECF为菱形;
(2)若CG⊥AD,CG,且∠CAD=30°,求菱形AECF的周长.
25.(10分)如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形AEFD是矩形;
(2)若AC BD=80,3CE=2CF,求OE的长.
26.(10分)如图1,在等边△ABC中,∠A=60°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想:图1中,线段PM与PN的数量关系是 ,∠MPN= ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,则上面题(1)中的两个结论是否依然成立,并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN周长的最大值
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D C B C C D B C C
11.120.
12..
13.3.
14.平行四边形(答案不唯一).
15.2.
16.10.
17. 3.
18.(1,﹣3)
19.解:如图,作∠MON的平分线OC,连接AB,作线段的垂直平分线与OC交于点P,则点P为抓捕点.
理由:角平分线上的点到角两边的距离相等(即犯罪分子在∠MON的角平分线上,点P也在其上),
线段垂直平分线上的点到线段两端点的距离相等(所以点P在线段AB的垂直平分线上).
∴两线的交点,即点P符合要求.
20.证明:∵AE⊥BD,CD⊥BD,
∴∠AEB=∠BDC=90°,
在Rt△ABE和Rt△BCD中,
,
∴Rt△ABE≌Rt△BCD(HL).
21.(1)证明:如图,连接BD,
∵四边形ABCD是菱形,∠ADC=120°,
∴AB=AD,∠ABC=∠ADC=120°,∠ADB∠ADC=60°,∠DBF∠ABC=60°,
∴△ABD是等边三角形,
∴AD=BD,∠A=∠ADB=60°,
∴∠A=∠DBF,
∵∠EDF=60°,
∴∠ADB﹣∠BDE=∠EDF﹣∠EDB,
即∠ADE=∠BDF,
∴△ADE≌△BDF(ASA),
∴DE=DF,
∴△DEF是等边三角形;
(2)解:如图,过点D作DM⊥AB于点M,
由(1)可知,△ADE≌△BDF,△ABD是等边三角形,
∴四边形BEDF的面积=△ABD的面积,AD=AB=4cm,AMAB=2(cm),
∴DM2(cm),
∴四边形BEDF的面积=△ABD的面积AB DM4×24(cm2).
22.(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是 ABCD的边BC、AD的中点,
∴AFAD,CEBC,
∴AF=CE,
又∵AF∥CE,
∴四边形AECF是平行四边形;
(2)解:∵BC=12,∠BAC=90°,E是BC的中点.
∴AE=CEBC=CE=6,
∴平行四边形AECF是菱形,
∴ AECF的周长=4×6=24.
23.解:如图所示,由题意得,
∠HAB=90°﹣60°=30°,∠MBC=90°﹣∠EBC=60°,
∵AH∥BM,
∴∠ABM=∠BAH=30°,
∴∠ABC=∠ABM+∠MBC=90°,
∵巡逻艇沿直线追赶,半小时后在点C处追上走私船,
∴BC=16×0.5=8(海里),
在Rt△ABC中,∠ABC=90°,AB=15海里,BC=8海里,
∴AC17(海里),
∴我军巡逻艇的航行速度是34(海里/小时).
答:我军巡逻艇的航行速度是34海里/小时.
24.(1)证明:∵EF垂直平分对角线AC,
∴AF=CF,AE=CE,OA=OC,
∴∠EAC=∠ECA,∠FAC=∠FCA,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAC=∠FCA,
∴∠FAO=∠ECO,
在△AOF和△COE中,
,
∴△AOF≌△COE(ASA),
∴AF=CE,
∵AD∥BC,
∴四边形AECF是平行四边形,
∵AF=CF,
∴平行四边形AECF为菱形;
(2)解:∵CG⊥AD,
∴∠CGA=90°,
∵∠CAD=30°,
∴AC=2CG=2,
∴AGCG3,
∵四边形AECF是菱形,
∴AE=CE=AF=CF,
设AF=CF=x,则FG=AG﹣AF=3﹣x,
在Rt△CFG中,由勾股定理得:CG2+FG2=CF2,
即()2+(3﹣x)2=x2,
解得:x=2,
∴AF=CF=2,
∴菱形AECF的周长=4AF=8.
25.(1)证明:∵四边形ABCD是菱形,
∴AD∥BC,AD=BC,
∵CF=BE,
∴CF+CE=BE+CE,
即EF=BC,
∴AD=EF,
∴四边形AEFD是平行四边形,
∵AE⊥BC,
∴∠AEF=90°,
∴平行四边形AEFD是矩形;
(2)解:设CE=2a(a>0),则BE=CF=3a,BC=BE+CE=5a,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∴∠BOC=90°,
∵AE⊥BC,
∴∠AEC=90°,
∴OEAC=OC,
∵cos∠ACE,
∴,
解得:OCa,
∴OB2a,
∵AC BD=80,
∴OA OC=20,
即a 2a=20,
解得:a(负值已舍去),
∴OEa,
即OE的长为.
26.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵AD=AE,
∴AB﹣AD=AC﹣AE,即BD=CE,
∵M,P,N分别是DE,DC,BC的中点,
∴MPEC,PM∥EC,PNBD,PN∥BD,
∴PM=PN,∠MPD=∠ACD,∠NPD=∠ADC,
在△ACD中,∠ADC+∠ACD=180°﹣∠A=120°,
∴∠MPN=∠MPD+∠NPD=120°.
故答案为:PM=PN,120°;
(2)(1)中的两个结论依然成立;理由如下:
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵DM=ME,DP=PC,BN=NC,
∴MPEC,PM∥EC,PNBD,PN∥BD,
∴MP=PN,
∴△PMN是等腰三角形.
∵PM∥CE,
∴∠DPM=∠DCE,
∵PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=60°,
∴∠ACB+∠ABC=120°,
∴∠MPN=120°,
∴PM=PN,∠MPN=120°;
(3)△PMN周长的最大值为14+7;理由如下:
由(2)知:PM=PN,∠MPN=120°,
∵BD≤AB+AD,
∴BD≤14,
∴点D恰好在BA延长线上时,BD、CE取得最大值,且最大值为14,
∴PM、PN的最大值为7,
此时MN经过点A,即MN垂直平分BC,如图,
∵△ABC、△ADE是等边三角形,且AD=4,AB=10,
∴∠BAN=∠DAM=30°,
∴BN=CN=5,DM=EM=2,
∴AN5,AM2,
∴△PMN周长的最大值为PM+PN+MN=7+7+5214+7.
第9页
同课章节目录
