2025年中考数学二轮复习 专题8 半角模型 课件 (共26张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习 专题8 半角模型 课件 (共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 485.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 17:25:46 | ||
图片预览




文档简介
(共26张PPT)
专题八 半角模型
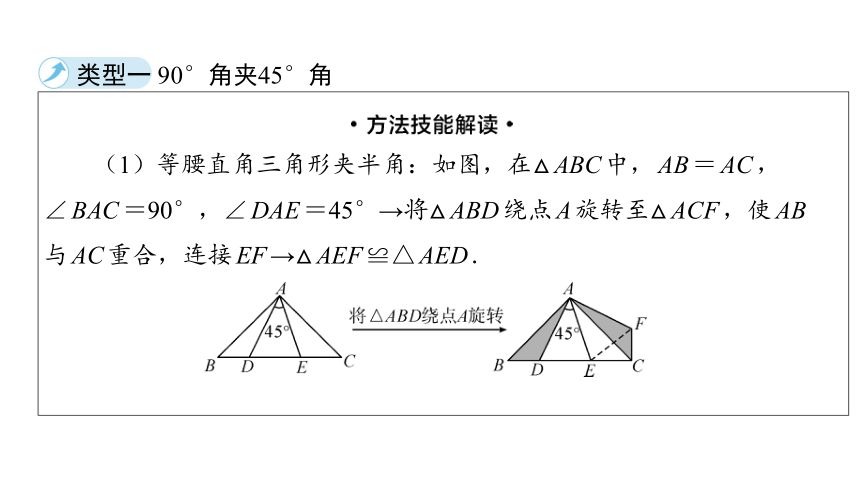
类型一 90°角夹45°角
(1)等腰直角三角形夹半角:如图,在△ABC中,AB=AC,
∠BAC=90°,∠DAE=45°→将△ABD绕点A旋转至△ACF,使AB
与AC重合,连接EF→△AEF≌△AED.
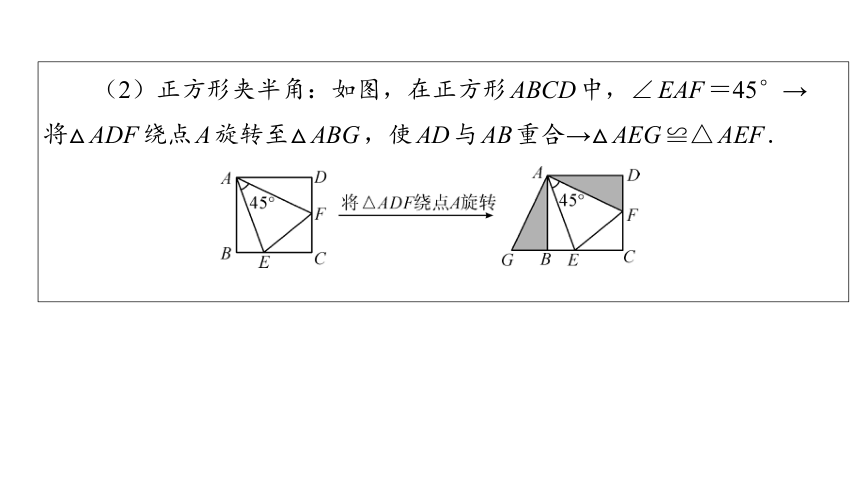
(2)正方形夹半角:如图,在正方形ABCD中,∠EAF=45°→
将△ADF绕点A旋转至△ABG,使AD与AB重合→△AEG≌△AEF.
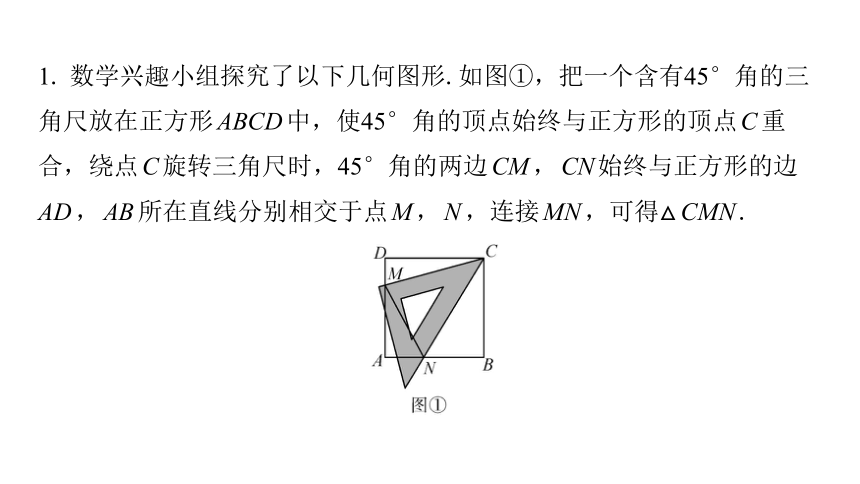
1. 数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三
角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重
合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边
AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
(1)如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到
点H在直线AB上,求证:∠CNM=∠CNH;
证明:(1)∵△CDM绕点C逆时针旋转90°得到△CBH,
∴CM=CH,∠DCM=∠BCH.
∵四边形ABCD为正方形,∴DCB=90°.∵∠MCN=45°,
∴∠DCM+∠BCN=∠DCB-∠MCN=45°,
∴∠BCH+∠BCN=45°,∴∠MCN=∠HCN=45°.
在△MCN和△HCN中,CM=CH,∠MCN=∠HCN,CN=CN,
∴△MCN≌△HCN(SAS),∴∠CNM=∠CNH.
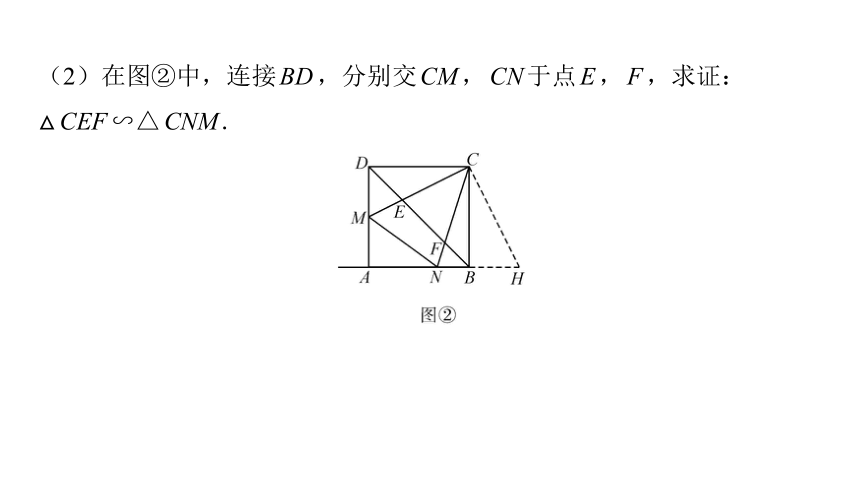
(2)在图②中,连接BD,分别交CM,CN于点E,F,求证:
△CEF∽△CNM.
(2)由(1)可得∠CNM=∠CNH. ∵四边形ABCD是正方形,BD是
对角线,∴∠FBN=∠MCN=45°,
∴△FBN∽△HCN∽△MCN,∴∠BFN=∠CMN. ∵∠BFN=
∠CFE,∴∠CFE=∠CMN.
又∵∠FCE=∠MCN,∴△CEF∽△CNM.
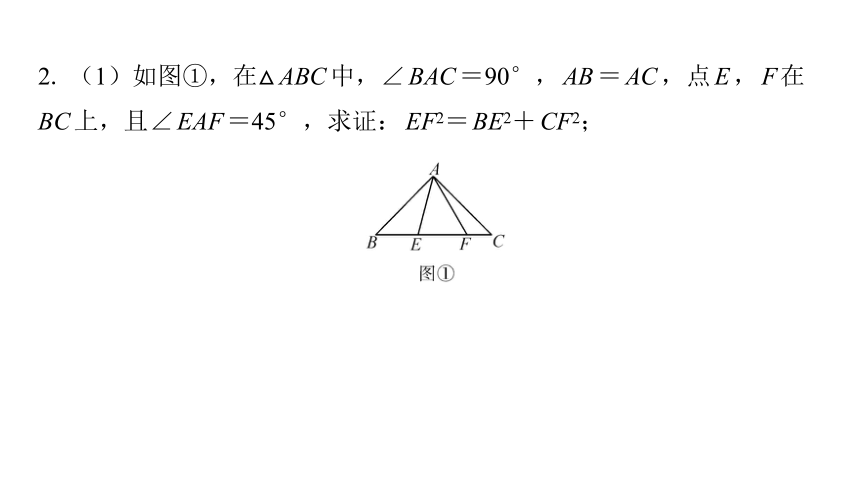
2. (1)如图①,在△ABC中,∠BAC=90°,AB=AC,点E,F在
BC上,且∠EAF=45°,求证:EF2=BE2+CF2;
(1)证明:如图①,将△ABE绕点A逆时针旋转90°得到△ACM,连
接MF,
则△ACM≌△ABE,
∴CM=BE,AM=AE,∠ACM=∠B=∠ACB=45°,
∴∠MCF=90°,即△MCF为直角三角形.
又易得△AMF≌△AEF(SAS),∴MF=EF.
在Rt△MCF中,MF2=MC2+CF2,∴EF2=BE2+CF2.
(2)如图②,在矩形ABCD中,点E,F分别在边BC,CD上,且
∠EAF=∠CEF=45°,若BE=3,DF=1,求EF的长.
(2)解:如图②,分别延长AD,AB与直线EF交于点M,N,将
△AFM绕点A顺时针旋转90°得到△AGN,连接EG.
∵∠CEF=45°,四边形ABCD是矩形,∴△DMF,△BEN都是等腰
直角三角形,
∴MF= DF= ,NE= BE=3 .
由(1)可得EF2=EG2=MF2+NE2,∴EF2= + =
20,EF=2 .
3. 如图,在正方形ABCD中,点M,N分别在边BC,CD上,且
∠MAN=45°,AH⊥MN于点H.
(1)求证:MN=BM+DN,AH=AB;
(1)证明:如图,将△ADN旋转至△ABE,则△ADN≌△ABE,
∴AE=AN,∠BAE=∠DAN,∠ABE=∠D=90°,∴∠ABE+
∠ABM=180°,
∴E,B,M三点共线.∵∠MAN=45°,
∴∠DAN+∠BAM=45°,
∴∠BAE+∠BAM=45°,即∠MAE=45°,
∴∠MAE=∠MAN. 又∵AE=AN,AM=AM,∴△AEM≌△ANM
(SAS),
∴MN=ME=BM+BE=BM+DN,∴S△AEM=S△ANM,∴ MN·AH
= ME·AB,∵MN=ME,∴AH=AB.
(2)若BM=2,DN=3,求AH的长.
(2)解:设AH=x.由(1)可得正方形的边长为x.∵BM=2,DN=
3,∴CM=x-2,CN=x-3.
由(1)可得MN=BM+DN=2+3=5.∵CN2+CM2=MN2,即(x-
3)2+(x-2)2=25,
解得x1=6,x2=-1(舍去),∴AH的长为6.
类型二 120°角夹60°角
如图,AB=AC=BC,BD=CD,∠BDC=120°,∠EDF=
60°→将△BDE绕点D旋转至△CDG,使DB与DC重合,连接
EF→△DFG≌△DFE.
1. 如图,D是等边三角形ABC外一点,且BD=CD,∠BDC=
120°,M,N分别是边AB,AC上一点,且∠MDN=60°.
(1)探索线段BM,MN,CN之间的数量关系,并说明理由;
解:(1)MN=BM+CN. 理由如下:
如图,将△MDB绕点D旋转至△HDC,则△HDC≌△MDB,
∴DH=DM,CH=BM,∠HDC=∠MDB,∠HCD=∠MBD.
易得∠MBD=∠NCD=90°,
∴∠HCD+∠NCD=180°,∴N,C,H三点共线.
又∵∠BDC=120°,∠MDN=60°,∴∠MDB+∠NDC=60°,∴∠HDC+∠NDC=60°,
∴∠HDN=∠MDN=60°.又∵DH=DM,DN=
DN,∴△HDN≌△MDN(SAS),
∴MN=HN=CH+CN=BM+CN.
(2)求△AMN与△ABC的周长的比值.
解:(2)C△AMN=AM+MN+AN=AB-BM+MN+AC-CN=
2AB+MN-(BM+CN).
由(1)可得MN=BM+CN,∴C△AMN=2AB,∴ = = .
2. [2024·龙东改编]如图,在△ABC中,AB=AC,∠MAN=
∠BAC,∠MAN在∠BAC内部,点M,N在BC上,点M在点N的左
侧.若∠BAC=120°,探究线段BM,NC,MN之间的数量关系.
解:∵∠BAC=120°,∴∠MAN=60°,∠ABC=∠C=30°.
如图,将△ANC绕点A顺时针旋转120°得到△AGB,
连接GM,则△AGB≌△ANC,
∴AG=AN,GB=NC,∠GAB=∠NAC,∠ABG=∠C=30°,
∴∠MAG=∠GAB+∠MAB=∠NAC+∠MAB=120°-∠MAN=60°,
∴∠MAG=∠MAN. ∵AG=AN,AM=AM,
∴△AGM≌△ANM(SAS),∴MG=MN.
过点G作GH⊥BC于点H(如图).∵∠GBH=60°,∴∠BGH=30°,
∴BH= GB= NC,GH= GB= NC,MH=BM-BH=BM- NC.
∵MG2=MH2+GH2,∴MN2= + ,
整理可得MN2=BM2+NC2-BM·NC.
谢谢观看
专题八 半角模型
类型一 90°角夹45°角
(1)等腰直角三角形夹半角:如图,在△ABC中,AB=AC,
∠BAC=90°,∠DAE=45°→将△ABD绕点A旋转至△ACF,使AB
与AC重合,连接EF→△AEF≌△AED.
(2)正方形夹半角:如图,在正方形ABCD中,∠EAF=45°→
将△ADF绕点A旋转至△ABG,使AD与AB重合→△AEG≌△AEF.
1. 数学兴趣小组探究了以下几何图形.如图①,把一个含有45°角的三
角尺放在正方形ABCD中,使45°角的顶点始终与正方形的顶点C重
合,绕点C旋转三角尺时,45°角的两边CM,CN始终与正方形的边
AD,AB所在直线分别相交于点M,N,连接MN,可得△CMN.
(1)如图②,把△CDM绕点C逆时针旋转90°得到△CBH,同时得到
点H在直线AB上,求证:∠CNM=∠CNH;
证明:(1)∵△CDM绕点C逆时针旋转90°得到△CBH,
∴CM=CH,∠DCM=∠BCH.
∵四边形ABCD为正方形,∴DCB=90°.∵∠MCN=45°,
∴∠DCM+∠BCN=∠DCB-∠MCN=45°,
∴∠BCH+∠BCN=45°,∴∠MCN=∠HCN=45°.
在△MCN和△HCN中,CM=CH,∠MCN=∠HCN,CN=CN,
∴△MCN≌△HCN(SAS),∴∠CNM=∠CNH.
(2)在图②中,连接BD,分别交CM,CN于点E,F,求证:
△CEF∽△CNM.
(2)由(1)可得∠CNM=∠CNH. ∵四边形ABCD是正方形,BD是
对角线,∴∠FBN=∠MCN=45°,
∴△FBN∽△HCN∽△MCN,∴∠BFN=∠CMN. ∵∠BFN=
∠CFE,∴∠CFE=∠CMN.
又∵∠FCE=∠MCN,∴△CEF∽△CNM.
2. (1)如图①,在△ABC中,∠BAC=90°,AB=AC,点E,F在
BC上,且∠EAF=45°,求证:EF2=BE2+CF2;
(1)证明:如图①,将△ABE绕点A逆时针旋转90°得到△ACM,连
接MF,
则△ACM≌△ABE,
∴CM=BE,AM=AE,∠ACM=∠B=∠ACB=45°,
∴∠MCF=90°,即△MCF为直角三角形.
又易得△AMF≌△AEF(SAS),∴MF=EF.
在Rt△MCF中,MF2=MC2+CF2,∴EF2=BE2+CF2.
(2)如图②,在矩形ABCD中,点E,F分别在边BC,CD上,且
∠EAF=∠CEF=45°,若BE=3,DF=1,求EF的长.
(2)解:如图②,分别延长AD,AB与直线EF交于点M,N,将
△AFM绕点A顺时针旋转90°得到△AGN,连接EG.
∵∠CEF=45°,四边形ABCD是矩形,∴△DMF,△BEN都是等腰
直角三角形,
∴MF= DF= ,NE= BE=3 .
由(1)可得EF2=EG2=MF2+NE2,∴EF2= + =
20,EF=2 .
3. 如图,在正方形ABCD中,点M,N分别在边BC,CD上,且
∠MAN=45°,AH⊥MN于点H.
(1)求证:MN=BM+DN,AH=AB;
(1)证明:如图,将△ADN旋转至△ABE,则△ADN≌△ABE,
∴AE=AN,∠BAE=∠DAN,∠ABE=∠D=90°,∴∠ABE+
∠ABM=180°,
∴E,B,M三点共线.∵∠MAN=45°,
∴∠DAN+∠BAM=45°,
∴∠BAE+∠BAM=45°,即∠MAE=45°,
∴∠MAE=∠MAN. 又∵AE=AN,AM=AM,∴△AEM≌△ANM
(SAS),
∴MN=ME=BM+BE=BM+DN,∴S△AEM=S△ANM,∴ MN·AH
= ME·AB,∵MN=ME,∴AH=AB.
(2)若BM=2,DN=3,求AH的长.
(2)解:设AH=x.由(1)可得正方形的边长为x.∵BM=2,DN=
3,∴CM=x-2,CN=x-3.
由(1)可得MN=BM+DN=2+3=5.∵CN2+CM2=MN2,即(x-
3)2+(x-2)2=25,
解得x1=6,x2=-1(舍去),∴AH的长为6.
类型二 120°角夹60°角
如图,AB=AC=BC,BD=CD,∠BDC=120°,∠EDF=
60°→将△BDE绕点D旋转至△CDG,使DB与DC重合,连接
EF→△DFG≌△DFE.
1. 如图,D是等边三角形ABC外一点,且BD=CD,∠BDC=
120°,M,N分别是边AB,AC上一点,且∠MDN=60°.
(1)探索线段BM,MN,CN之间的数量关系,并说明理由;
解:(1)MN=BM+CN. 理由如下:
如图,将△MDB绕点D旋转至△HDC,则△HDC≌△MDB,
∴DH=DM,CH=BM,∠HDC=∠MDB,∠HCD=∠MBD.
易得∠MBD=∠NCD=90°,
∴∠HCD+∠NCD=180°,∴N,C,H三点共线.
又∵∠BDC=120°,∠MDN=60°,∴∠MDB+∠NDC=60°,∴∠HDC+∠NDC=60°,
∴∠HDN=∠MDN=60°.又∵DH=DM,DN=
DN,∴△HDN≌△MDN(SAS),
∴MN=HN=CH+CN=BM+CN.
(2)求△AMN与△ABC的周长的比值.
解:(2)C△AMN=AM+MN+AN=AB-BM+MN+AC-CN=
2AB+MN-(BM+CN).
由(1)可得MN=BM+CN,∴C△AMN=2AB,∴ = = .
2. [2024·龙东改编]如图,在△ABC中,AB=AC,∠MAN=
∠BAC,∠MAN在∠BAC内部,点M,N在BC上,点M在点N的左
侧.若∠BAC=120°,探究线段BM,NC,MN之间的数量关系.
解:∵∠BAC=120°,∴∠MAN=60°,∠ABC=∠C=30°.
如图,将△ANC绕点A顺时针旋转120°得到△AGB,
连接GM,则△AGB≌△ANC,
∴AG=AN,GB=NC,∠GAB=∠NAC,∠ABG=∠C=30°,
∴∠MAG=∠GAB+∠MAB=∠NAC+∠MAB=120°-∠MAN=60°,
∴∠MAG=∠MAN. ∵AG=AN,AM=AM,
∴△AGM≌△ANM(SAS),∴MG=MN.
过点G作GH⊥BC于点H(如图).∵∠GBH=60°,∴∠BGH=30°,
∴BH= GB= NC,GH= GB= NC,MH=BM-BH=BM- NC.
∵MG2=MH2+GH2,∴MN2= + ,
整理可得MN2=BM2+NC2-BM·NC.
谢谢观看
同课章节目录
