华师大版七下(2024版)9.1.4设计轴对称图案学案
文档属性
| 名称 | 华师大版七下(2024版)9.1.4设计轴对称图案学案 |

|
|
| 格式 | docx | ||
| 文件大小 | 851.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-06 08:56:10 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第9章轴对称、平移与旋转
9.1.4 设计轴对称图案
学习目标与重难点
学习目标:1.能准确描述轴对称图案设计步骤,掌握 “定点—连线—对称” 操作法;熟练用折纸等工具设计制作至少2种轴对称图案,分析其设计原理,解决相关问题.
2.经过 “观察—模仿—创新” 探究,进行图案设计思维训练;小组合作分工完成复杂图案设计,借助数学软件理解计算机辅助设计流程.
3.感受轴对称图案美,增强数学美学认知;在设计中体验创新乐趣,认识数学在文化传承与现代设计中的应用,培养学科融合意识.
学习重点:1.掌握轴对称图案的设计流程(确定对称轴→设计基本图形→对称复制),能运用折纸、剪纸等工具完成简单图案制作.
2.分析生活中轴对称图案的构成原理(如对称轴数量、基本图形组合方式).
学习难点:将数学对称原理与艺术创意结合,设计出兼具对称性和主题内涵的原创图案(如结合 “环保”“节日” 等主题融入对称元素).
预习自测
知识链接
1.线段有几条对称轴?圆有几条对称轴.
2.设计轴对称图案时,图案的颜色和阴影需要对称吗?
自学自测
1.榫卯是中国建筑的智慧结晶,仅靠木头之间的相互作用力就可以让建筑或家具牢固、美观.下列榫卯拼接的截面示意图中,是轴对称图形的是 ( )
A B
C D
2.如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随便选1个涂成黑色,画出完整的图案为轴对称图案,符合题意的图案共有几种?
教学过程
一、创设情境、导入新课
如图所示,以虚线为对称轴画出图形的另一半.
既然同学们学会了画对称图形,今天我们就来利用对称图形设计图案.
二、合作交流、新知探究
探究一:
教材第125页:
在商标、衣料图案和众多的日用品上,我们可以看到不少丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形.
他们是怎么设计出来的呢?
思考:图 9.1.19 是两个轴对称图形, 它们有多少条对称轴? 我们可以利用轴对称的方法来作出它们吗?
上图有几条对称轴?请画出来.
请准备一张正方形纸片, 按图 9.1.20 所示的 5 个步骤来作:
(1)如图 9.1.20①, 在正方形纸片上用虚线作出 4 条对称轴;
(2)如图 9.1.20②, 在其中一个三角形中, 作出图形形状的基本线条(注意: 不同的线条最终会得到不同的图案, 你可以自己设计线条, 而不必和教科书中的一样);
(3)如图 9.1.20③, 按照其中一条斜的对称轴作出(2)中图形的对称图形;
(4)如图 9.1.20④, 按照另一条斜的对称轴作出(3)中图形的对称图形;
(5)如图 9.1.20⑤, 按照水平(或垂直)的对称轴作出(4)中图形的对称图形, 从而得到图 9.1.19①中的图形.
作好之后,你可以在图案上涂上你喜欢的颜色,擦掉其他多余的线条,一幅对称的图案就完成了.
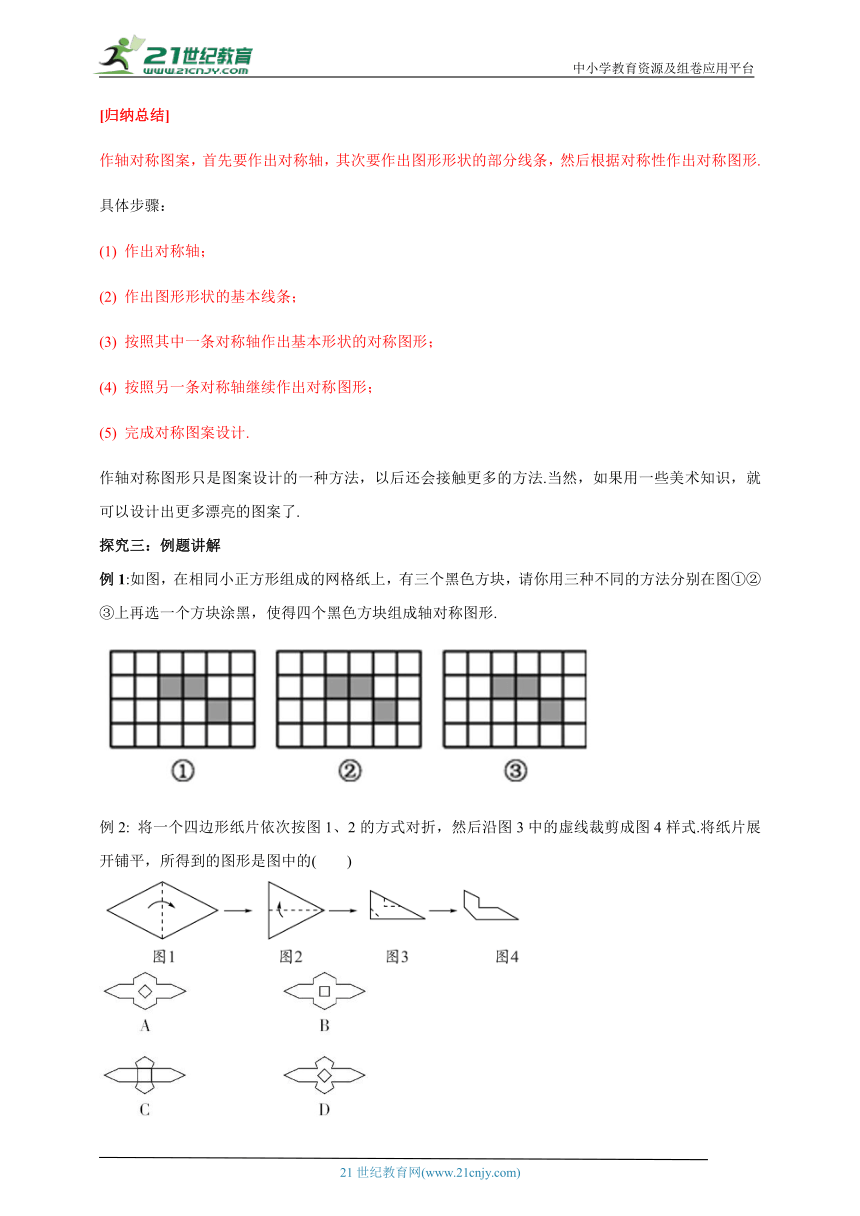
[归纳总结]
作轴对称图案,首先要作出对称轴,其次要作出图形形状的部分线条,然后根据对称性作出对称图形.
具体步骤:
(1) 作出对称轴;
(2) 作出图形形状的基本线条;
(3) 按照其中一条对称轴作出基本形状的对称图形;
(4) 按照另一条对称轴继续作出对称图形;
(5) 完成对称图案设计.
作轴对称图形只是图案设计的一种方法,以后还会接触更多的方法.当然,如果用一些美术知识,就可以设计出更多漂亮的图案了.
探究三:例题讲解
例1:如图,在相同小正方形组成的网格纸上,有三个黑色方块,请你用三种不同的方法分别在图①②③上再选一个方块涂黑,使得四个黑色方块组成轴对称图形.
例2: 将一个四边形纸片依次按图1、2的方式对折,然后沿图3中的虚线裁剪成图4样式.将纸片展开铺平,所得到的图形是图中的( )
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.下列设计的图形中,属于轴对称图形的是( )
2.“二十四节气”是根据太阳在黄道(即地球绕太阳公转的轨道)上的位置来划分的,是在我国春秋战国时期确立的一种用来指导农事的补充历法,如图设计的四幅“二十四节气”标识图中,除去文字后的图案是轴对称图形的是( )
3.如图所示,两个孩子的球衣上的号码是( )
A.53,12 B.23,15 C.53,15 D.23,12
选做题:
4.把如图图形补成以直线l为对称轴的轴对称图形.
5.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC
C.ED+EB=DB D.AE+CB=AB
6.如图,在△ABC中,点D在BC边上,点D关于AB,AC对称的对称点分别为E,F,连结AE,AF.如图所示,∠EAF的度数是( )
A.113° B.124° C.129° D.134°
【综合拓展类作业】
7.如图,点D,E,F分别在△ABC的各边上,DE∥AC,DF∥AB.将△ABC沿DE翻折,使得点B落在B'处,沿DF翻折,使得点C落在C'处.若∠B'DC'=40°,则∠A= °.
8.一个四边形纸片ABCD,∠B=∠D,把纸片按如图所示折叠,使点B落在AD边上的F点,AE是折痕,若∠C=72°,求∠AEB的度数.
解:因为△AFE与△ABE关于AE成轴对称(已知),
所以∠AEB=∠AEF,∠B=∠AFE(成轴对称的两个图形的对应角相等)
……
请补全说理过程.
总结反思、拓展升华
【课堂总结】
知识点:设计轴对称图案的具体步骤:
(1) 作出对称轴;
(2) 作出图形形状的基本线条;
(3) 按照其中一条对称轴作出基本形状的对称图形;
(4) 按照另一条对称轴继续作出对称图形;
(5) 完成对称图案设计.
五、【作业布置】
【知识技能类作业】
必做题:
1.右图是由“”和“”组成的轴对称图形,该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
2.小华将一张如图所示的长方形纸片沿对角线剪开,她将所得的两个直角三角形通过图形变换构成了如图所示的四个图形,这四个图形中不是轴对称图形的是( )
3.如图所示,要使图形是轴对称图形,适合放进图中内的是图中的( )
选做题:
4.一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,那么下列图案中不符合要求的是( )
5.如图,在正方形方格中,阴影部分是由7个涂黑的小正方形所形成的图案,再将方格内一个空白的小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有________种.
6.现有由9个相同的小等边三角形拼成的一个大等边三角形,将其中部分涂黑,如图 (1)和(2)所示,观察发现图(1)和图(2)中被涂黑部分的图案具有两个特征:①都是轴对称图案;②被涂黑部分都是小等边三角形.请在图(3)、图(4)内分别设计一个新图案,使新图案也具有上述两个特征.
【综合拓展类作业】
7.如图①为L形的一种三格骨牌,它是由三个全等的正方形连接而成的.请以L形的三格骨牌为基本图形,在图②和图③中各设计一个轴对称图形.要求如下:
(1)每个图形由3个L形三格骨牌组成,骨牌的顶点都在小正方形的顶点上;
(2)在设计的图形上画上斜线,若形状相同,则视为一种.
8 在由四个相同的小正方形组成的“7”字形图中,请你再添加一个小正方形,使整个图形成为轴对称图形,并用虚线画出它的对称轴.要求在图10中画出三种不同的设计图案(不要求尺规作图).
答案:
自学测试:
1.C
2.解:如图所示.符合题意的图案共有2种.
课堂巩固:
1.D;2.B;3.B;
4. 【解析】如图所示:
5.D;6.D;7.70
8. 【解析】因为△AFE与△ABE关于AE成轴对称(已知),
所以∠AEB=∠AEF,∠B=∠AFE(成轴对称的两个图形的对应角相等),
∵∠B=∠D,∴∠AFE=∠D,∴FE∥CD.
∴∠FEB=∠C=72°,∴∠AEB=∠AEF=∠BEF=36°.
作业布置:
1.[解析] C 分别沿着图中的4条直线进行折叠,能使直线两侧完全重合的只有直线l3,故选C.
2.[解析] A 根据轴对称图形的定义 “如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形”,可知A项中的图形不是轴对称图形.
3.[解析] C 图形的上下部分已经是轴对称图形,中间要放进的图形应与左边的三角形成轴对称,三角形的放法只有选项C,选项B不能构成轴对称图形.故选C.
4.[解析] D A项,图形关于正方形的对角线所在的直线对称,两条对角线所在的直线都是其对称轴;B项,图形关于正方形对角线所在的直线对称,两条对角线所在的直线都是其对称轴;C项,图形关于正方形的对角线所在的直线对称,有一条对称轴;D项,图形关于正方形对角线所在的直线不对称.故选D.
5.[答案] 3
[解析] 如图,根据正方形的对称性,在图中的1,2,3处分别涂黑都可得到一个轴对称图形,故涂法有3种.
6.解:答案不唯一,如图所示.
7.[解析] 可以利用轴对称设计一个图案,再利用平移设计一个图案.
解:(答案不唯一)如图所示.
8 解:如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第9章轴对称、平移与旋转
9.1.4 设计轴对称图案
学习目标与重难点
学习目标:1.能准确描述轴对称图案设计步骤,掌握 “定点—连线—对称” 操作法;熟练用折纸等工具设计制作至少2种轴对称图案,分析其设计原理,解决相关问题.
2.经过 “观察—模仿—创新” 探究,进行图案设计思维训练;小组合作分工完成复杂图案设计,借助数学软件理解计算机辅助设计流程.
3.感受轴对称图案美,增强数学美学认知;在设计中体验创新乐趣,认识数学在文化传承与现代设计中的应用,培养学科融合意识.
学习重点:1.掌握轴对称图案的设计流程(确定对称轴→设计基本图形→对称复制),能运用折纸、剪纸等工具完成简单图案制作.
2.分析生活中轴对称图案的构成原理(如对称轴数量、基本图形组合方式).
学习难点:将数学对称原理与艺术创意结合,设计出兼具对称性和主题内涵的原创图案(如结合 “环保”“节日” 等主题融入对称元素).
预习自测
知识链接
1.线段有几条对称轴?圆有几条对称轴.
2.设计轴对称图案时,图案的颜色和阴影需要对称吗?
自学自测
1.榫卯是中国建筑的智慧结晶,仅靠木头之间的相互作用力就可以让建筑或家具牢固、美观.下列榫卯拼接的截面示意图中,是轴对称图形的是 ( )
A B
C D
2.如图,在“3×3”网格中,有3个涂成黑色的小方格.若再从余下的6个小方格中随便选1个涂成黑色,画出完整的图案为轴对称图案,符合题意的图案共有几种?
教学过程
一、创设情境、导入新课
如图所示,以虚线为对称轴画出图形的另一半.
既然同学们学会了画对称图形,今天我们就来利用对称图形设计图案.
二、合作交流、新知探究
探究一:
教材第125页:
在商标、衣料图案和众多的日用品上,我们可以看到不少丰富多彩的装饰图案,仔细观察这些装饰图案,你会发现其中有许多轴对称图形.
他们是怎么设计出来的呢?
思考:图 9.1.19 是两个轴对称图形, 它们有多少条对称轴? 我们可以利用轴对称的方法来作出它们吗?
上图有几条对称轴?请画出来.
请准备一张正方形纸片, 按图 9.1.20 所示的 5 个步骤来作:
(1)如图 9.1.20①, 在正方形纸片上用虚线作出 4 条对称轴;
(2)如图 9.1.20②, 在其中一个三角形中, 作出图形形状的基本线条(注意: 不同的线条最终会得到不同的图案, 你可以自己设计线条, 而不必和教科书中的一样);
(3)如图 9.1.20③, 按照其中一条斜的对称轴作出(2)中图形的对称图形;
(4)如图 9.1.20④, 按照另一条斜的对称轴作出(3)中图形的对称图形;
(5)如图 9.1.20⑤, 按照水平(或垂直)的对称轴作出(4)中图形的对称图形, 从而得到图 9.1.19①中的图形.
作好之后,你可以在图案上涂上你喜欢的颜色,擦掉其他多余的线条,一幅对称的图案就完成了.
[归纳总结]
作轴对称图案,首先要作出对称轴,其次要作出图形形状的部分线条,然后根据对称性作出对称图形.
具体步骤:
(1) 作出对称轴;
(2) 作出图形形状的基本线条;
(3) 按照其中一条对称轴作出基本形状的对称图形;
(4) 按照另一条对称轴继续作出对称图形;
(5) 完成对称图案设计.
作轴对称图形只是图案设计的一种方法,以后还会接触更多的方法.当然,如果用一些美术知识,就可以设计出更多漂亮的图案了.
探究三:例题讲解
例1:如图,在相同小正方形组成的网格纸上,有三个黑色方块,请你用三种不同的方法分别在图①②③上再选一个方块涂黑,使得四个黑色方块组成轴对称图形.
例2: 将一个四边形纸片依次按图1、2的方式对折,然后沿图3中的虚线裁剪成图4样式.将纸片展开铺平,所得到的图形是图中的( )
三、课堂练习、巩固提高
【知识技能类作业】
必做题:
1.下列设计的图形中,属于轴对称图形的是( )
2.“二十四节气”是根据太阳在黄道(即地球绕太阳公转的轨道)上的位置来划分的,是在我国春秋战国时期确立的一种用来指导农事的补充历法,如图设计的四幅“二十四节气”标识图中,除去文字后的图案是轴对称图形的是( )
3.如图所示,两个孩子的球衣上的号码是( )
A.53,12 B.23,15 C.53,15 D.23,12
选做题:
4.把如图图形补成以直线l为对称轴的轴对称图形.
5.如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是( )
A.AD=BD B.BE=AC
C.ED+EB=DB D.AE+CB=AB
6.如图,在△ABC中,点D在BC边上,点D关于AB,AC对称的对称点分别为E,F,连结AE,AF.如图所示,∠EAF的度数是( )
A.113° B.124° C.129° D.134°
【综合拓展类作业】
7.如图,点D,E,F分别在△ABC的各边上,DE∥AC,DF∥AB.将△ABC沿DE翻折,使得点B落在B'处,沿DF翻折,使得点C落在C'处.若∠B'DC'=40°,则∠A= °.
8.一个四边形纸片ABCD,∠B=∠D,把纸片按如图所示折叠,使点B落在AD边上的F点,AE是折痕,若∠C=72°,求∠AEB的度数.
解:因为△AFE与△ABE关于AE成轴对称(已知),
所以∠AEB=∠AEF,∠B=∠AFE(成轴对称的两个图形的对应角相等)
……
请补全说理过程.
总结反思、拓展升华
【课堂总结】
知识点:设计轴对称图案的具体步骤:
(1) 作出对称轴;
(2) 作出图形形状的基本线条;
(3) 按照其中一条对称轴作出基本形状的对称图形;
(4) 按照另一条对称轴继续作出对称图形;
(5) 完成对称图案设计.
五、【作业布置】
【知识技能类作业】
必做题:
1.右图是由“”和“”组成的轴对称图形,该图形的对称轴是直线( )
A.l1 B.l2 C.l3 D.l4
2.小华将一张如图所示的长方形纸片沿对角线剪开,她将所得的两个直角三角形通过图形变换构成了如图所示的四个图形,这四个图形中不是轴对称图形的是( )
3.如图所示,要使图形是轴对称图形,适合放进图中内的是图中的( )
选做题:
4.一名同学想用正方形和圆设计一个图案,要求整个图案关于正方形的某条对角线对称,那么下列图案中不符合要求的是( )
5.如图,在正方形方格中,阴影部分是由7个涂黑的小正方形所形成的图案,再将方格内一个空白的小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有________种.
6.现有由9个相同的小等边三角形拼成的一个大等边三角形,将其中部分涂黑,如图 (1)和(2)所示,观察发现图(1)和图(2)中被涂黑部分的图案具有两个特征:①都是轴对称图案;②被涂黑部分都是小等边三角形.请在图(3)、图(4)内分别设计一个新图案,使新图案也具有上述两个特征.
【综合拓展类作业】
7.如图①为L形的一种三格骨牌,它是由三个全等的正方形连接而成的.请以L形的三格骨牌为基本图形,在图②和图③中各设计一个轴对称图形.要求如下:
(1)每个图形由3个L形三格骨牌组成,骨牌的顶点都在小正方形的顶点上;
(2)在设计的图形上画上斜线,若形状相同,则视为一种.
8 在由四个相同的小正方形组成的“7”字形图中,请你再添加一个小正方形,使整个图形成为轴对称图形,并用虚线画出它的对称轴.要求在图10中画出三种不同的设计图案(不要求尺规作图).
答案:
自学测试:
1.C
2.解:如图所示.符合题意的图案共有2种.
课堂巩固:
1.D;2.B;3.B;
4. 【解析】如图所示:
5.D;6.D;7.70
8. 【解析】因为△AFE与△ABE关于AE成轴对称(已知),
所以∠AEB=∠AEF,∠B=∠AFE(成轴对称的两个图形的对应角相等),
∵∠B=∠D,∴∠AFE=∠D,∴FE∥CD.
∴∠FEB=∠C=72°,∴∠AEB=∠AEF=∠BEF=36°.
作业布置:
1.[解析] C 分别沿着图中的4条直线进行折叠,能使直线两侧完全重合的只有直线l3,故选C.
2.[解析] A 根据轴对称图形的定义 “如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形”,可知A项中的图形不是轴对称图形.
3.[解析] C 图形的上下部分已经是轴对称图形,中间要放进的图形应与左边的三角形成轴对称,三角形的放法只有选项C,选项B不能构成轴对称图形.故选C.
4.[解析] D A项,图形关于正方形的对角线所在的直线对称,两条对角线所在的直线都是其对称轴;B项,图形关于正方形对角线所在的直线对称,两条对角线所在的直线都是其对称轴;C项,图形关于正方形的对角线所在的直线对称,有一条对称轴;D项,图形关于正方形对角线所在的直线不对称.故选D.
5.[答案] 3
[解析] 如图,根据正方形的对称性,在图中的1,2,3处分别涂黑都可得到一个轴对称图形,故涂法有3种.
6.解:答案不唯一,如图所示.
7.[解析] 可以利用轴对称设计一个图案,再利用平移设计一个图案.
解:(答案不唯一)如图所示.
8 解:如图所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
