湘教版数学九年级上册 4.1.1 正弦及30°角的正弦值 课件 (共25张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 4.1.1 正弦及30°角的正弦值 课件 (共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
第四章 锐角三角函数 4.1
正弦和余弦
4.1.1 正弦及30°角的正弦值
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
下图是上海东方明珠电视塔的远景图,你能想办法求出该塔的高度吗?
新课导入
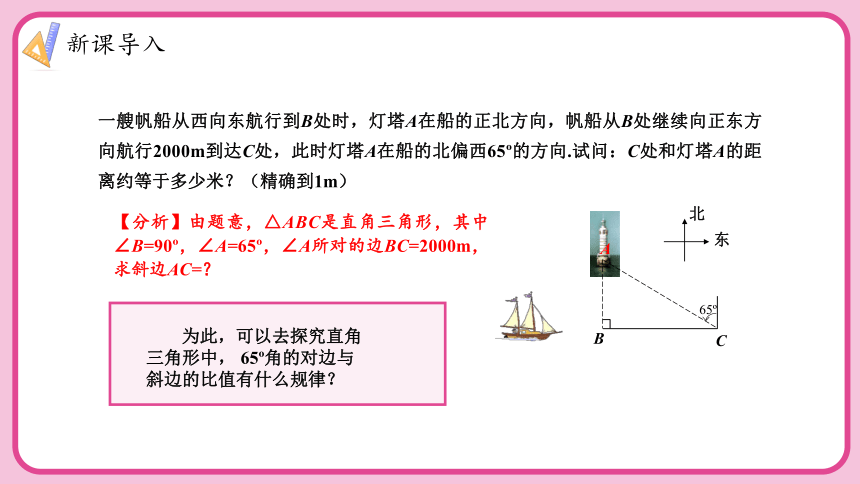
一艘帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
北
东
65
A
B
C
【分析】由题意,△ABC是直角三角形,其中∠B=90 ,∠A=65 ,∠A所对的边BC=2000m,求斜边AC=?
为此,可以去探究直角三角形中, 65 角的对边与斜边的比值有什么规律?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
做一做
画一个直角三角形,其中一个锐角为65°,量出65°角的对边长度和斜边长度,计算
65°角的对边
斜边
=_____________=_____________.
与同桌和邻桌的同学交流,看看计算出的比值是否相等(精确到0.01).
新课讲解
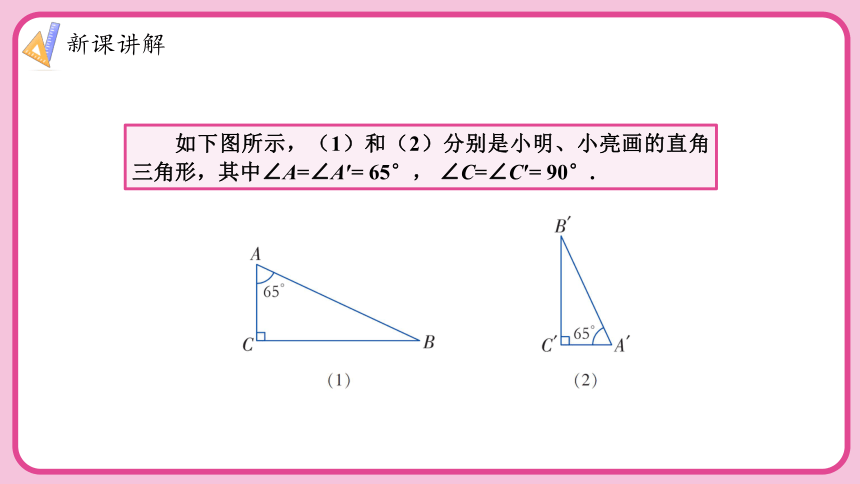
如下图所示,(1)和(2)分别是小明、小亮画的直角三角形,其中∠A=∠A′= 65°, ∠C=∠C′= 90°.
新课讲解
小明量出∠A的对边BC=3cm,斜边AB=3.3cm,算出:
小亮量出∠A′的对边B′C′=2cm, 斜边A′B′=2.2cm, 算出:
新课讲解
由此猜测:在有一个锐角为65°的所有直角三角形中,65°角的对边与斜边的比值是一个常数,它等于 .
这个猜测是真的吗? 若把65°角换成任意一个锐角α,则这个角的对边与斜边的比值是否也是一个常数呢?
新课讲解
如图,△ABC和△DEF都是直角三角形,其中∠A=∠D=α. ∠C=∠F=90°,则 成立吗?为什么?
新课讲解
∵∠A=∠D =α,∠C=∠F= 90°,
∴Rt△ABC∽Rt△DEF.
即BC·DE=AB·EF ,
这说明,在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值是一个常数,与直角三角形的大小无关.
新课讲解
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sin α,即
归纳小结
说 明:
1. sin α是在直角三角形中定义的,∠α是锐角(注意数形结合,构造直角三角形).
2. sin α是一个完整的符号,如:sin α不是sin与α的乘积,而是一个整体,表示∠ α的正弦.
3. sin α是两条线段的一个比值. 注意比的顺序,且0<sin α< 1,无单位.
4. sin α的大小只与∠α的大小有关,而与直角三角形的边长无关.
新课讲解
一艘帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
北
东
65
A
B
C
解:在Rt△ABC中,BC=2000m ,∠A= 65 ,
新课讲解
思考:在直角三角形中,30°角所对的直角边与斜边有什么关系?
在直角三角形中,30°角所对的直角边等于斜边的一半。
新课讲解
例1:如图所示,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求 sin A 的值;
(2)求 sin B 的值.
解(1)∠A的对边BC=3,斜边AB=5.
于是
新课讲解
例1:如图所示,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求 sin A 的值;
(2)求 sin B 的值.
(2)∠B的对边是AC,根据勾股定理,得
AC2= AB2-BC2= 52-32=16.
于是AC=4.
因此
新课讲解
1.如图,在直角三角形ABC中,∠C=90°,AB=13,BC=5.求sin A,sin B的值.
【选自教材P111 练习 第1题】
课堂练习
解:∠A的对边BC=5,斜边AB=13.
∠B的对边是AC,根据勾股定理,得
AC2= AB2-BC2= 132-52=144.
于是AC=12.
于是
因此
课堂练习
2.如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
解:如图,过点P作x轴的垂线,垂足为A,则点A坐标为(3,0).
A
在Rt△APO中,由勾股定理得
OP2= AP2+AO2= 42+32=25.
于是OP=5.
因此
【选自教材P111 练习 第2题】
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sin α,即
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第四章 锐角三角函数 4.1
正弦和余弦
4.1.1 正弦及30°角的正弦值
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
下图是上海东方明珠电视塔的远景图,你能想办法求出该塔的高度吗?
新课导入
一艘帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
北
东
65
A
B
C
【分析】由题意,△ABC是直角三角形,其中∠B=90 ,∠A=65 ,∠A所对的边BC=2000m,求斜边AC=?
为此,可以去探究直角三角形中, 65 角的对边与斜边的比值有什么规律?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
做一做
画一个直角三角形,其中一个锐角为65°,量出65°角的对边长度和斜边长度,计算
65°角的对边
斜边
=_____________=_____________.
与同桌和邻桌的同学交流,看看计算出的比值是否相等(精确到0.01).
新课讲解
如下图所示,(1)和(2)分别是小明、小亮画的直角三角形,其中∠A=∠A′= 65°, ∠C=∠C′= 90°.
新课讲解
小明量出∠A的对边BC=3cm,斜边AB=3.3cm,算出:
小亮量出∠A′的对边B′C′=2cm, 斜边A′B′=2.2cm, 算出:
新课讲解
由此猜测:在有一个锐角为65°的所有直角三角形中,65°角的对边与斜边的比值是一个常数,它等于 .
这个猜测是真的吗? 若把65°角换成任意一个锐角α,则这个角的对边与斜边的比值是否也是一个常数呢?
新课讲解
如图,△ABC和△DEF都是直角三角形,其中∠A=∠D=α. ∠C=∠F=90°,则 成立吗?为什么?
新课讲解
∵∠A=∠D =α,∠C=∠F= 90°,
∴Rt△ABC∽Rt△DEF.
即BC·DE=AB·EF ,
这说明,在有一个锐角等于α的所有直角三角形中,角α的对边与斜边的比值是一个常数,与直角三角形的大小无关.
新课讲解
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sin α,即
归纳小结
说 明:
1. sin α是在直角三角形中定义的,∠α是锐角(注意数形结合,构造直角三角形).
2. sin α是一个完整的符号,如:sin α不是sin与α的乘积,而是一个整体,表示∠ α的正弦.
3. sin α是两条线段的一个比值. 注意比的顺序,且0<sin α< 1,无单位.
4. sin α的大小只与∠α的大小有关,而与直角三角形的边长无关.
新课讲解
一艘帆船从西向东航行到B处时,灯塔A在船的正北方向,帆船从B处继续向正东方向航行2000m到达C处,此时灯塔A在船的北偏西65 的方向.试问:C处和灯塔A的距离约等于多少米?(精确到1m)
北
东
65
A
B
C
解:在Rt△ABC中,BC=2000m ,∠A= 65 ,
新课讲解
思考:在直角三角形中,30°角所对的直角边与斜边有什么关系?
在直角三角形中,30°角所对的直角边等于斜边的一半。
新课讲解
例1:如图所示,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求 sin A 的值;
(2)求 sin B 的值.
解(1)∠A的对边BC=3,斜边AB=5.
于是
新课讲解
例1:如图所示,在Rt△ABC中,∠C=90°,BC=3,AB=5.
(1)求 sin A 的值;
(2)求 sin B 的值.
(2)∠B的对边是AC,根据勾股定理,得
AC2= AB2-BC2= 52-32=16.
于是AC=4.
因此
新课讲解
1.如图,在直角三角形ABC中,∠C=90°,AB=13,BC=5.求sin A,sin B的值.
【选自教材P111 练习 第1题】
课堂练习
解:∠A的对边BC=5,斜边AB=13.
∠B的对边是AC,根据勾股定理,得
AC2= AB2-BC2= 132-52=144.
于是AC=12.
于是
因此
课堂练习
2.如图,在平面直角坐标系内有一点P(3,4),连接OP,求OP与x轴正方向所夹锐角α的正弦值.
解:如图,过点P作x轴的垂线,垂足为A,则点A坐标为(3,0).
A
在Rt△APO中,由勾股定理得
OP2= AP2+AO2= 42+32=25.
于是OP=5.
因此
【选自教材P111 练习 第2题】
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如图,在直角三角形中,我们把锐角α的对边与斜边的比叫作角α的正弦,记作sin α,即
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
