湘教版数学九年级上册 4.4.1 与俯角、仰角有关的实际问题 课件 (共24张PPT)
文档属性
| 名称 | 湘教版数学九年级上册 4.4.1 与俯角、仰角有关的实际问题 课件 (共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-17 17:36:44 | ||
图片预览






文档简介
(共24张PPT)
第四章 锐角三角函数 4.4
解直角三角形的应用
湘教版(2024)九年级上册数学课件
4.4.1 与俯角、仰角有关的实际问题
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
新课导入
海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行.
北
东
你认为货轮继续向东航行途中会有触礁的危险吗?
新课导入
北
东
D
分析:判断继续向东航行是否会有触礁危险,就是求AD的长度是否小于10海里.
在在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究新知
动脑筋
某探险者某天到达如图所示的点A处时,他准备估算出离他的目的地——海拔为3500m的山峰顶点B处的水平距离.你能帮他想出一个可行的办法吗?
新课讲解
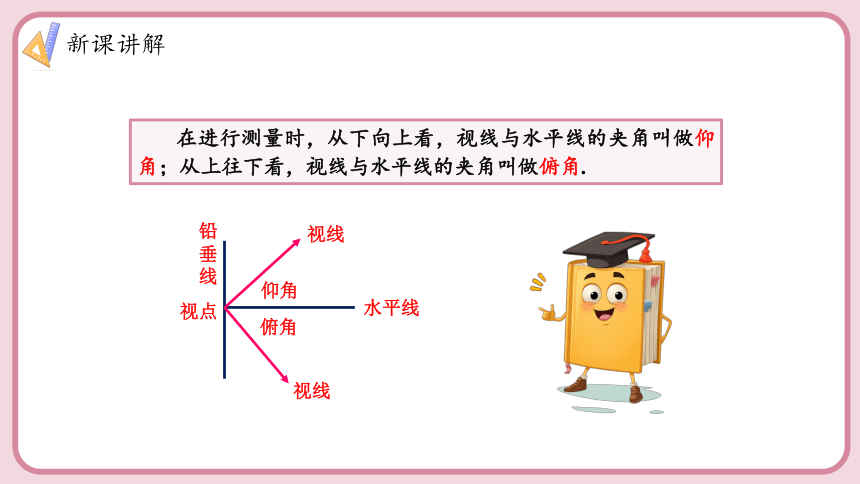
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
铅垂线
水平线
视线
视线
仰角
俯角
视点
新课讲解
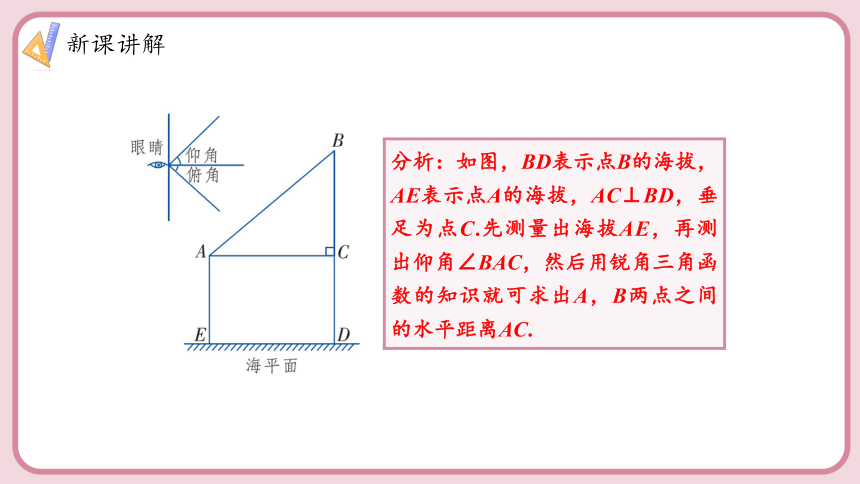
分析:如图,BD表示点B的海拔,AE表示点A的海拔,AC⊥BD,垂足为点C.先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
新课讲解
如图,如果测得点A的海拔AE为1600m,仰角∠BAC=40°求A,B两点之间的水平距离AC(结果保留整数).
∵ BD = 3500m,AE = 1600m,AC⊥BD,∠BAC = 40°,
∴ 在Rt△ABC中,
∴
即AC≈2264(m).
因此,A,B两点之间的水平距离AC约为2264 m.
新课讲解
例1:如图, 在离上海东方明珠塔底部1000m的A处,用仪器测得塔顶的仰角∠BAC为25°,仪器距地面高AE为1.7m.求上海东方明珠塔的高度BD(结果精确到1m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
新课讲解
解:如图,在Rt△ABC中,∠BAC=25°,AC=1000 m,因此
从而BC=1000 × tan 25°≈ 466.3(m).
因此,上海东方明珠塔的高度
BD=466.3 + 1.7 = 468(m).
答:上海东方明珠塔的高度BD为468 m.
新课讲解
1.如图,一艘游船在离开码头A后,以和河岸成 30°角的方向行驶了500m到达B处,求B处与河岸的距离BC.
【选自教材P126 练习 第1题】
课堂练习
解:从点B作河岸线(看成直线段)的垂线,垂足为C,
在Rt△ABC中,∠C=90°,∠A=30°,AB=500m.
由于BC是∠A的对边,AB是斜边,因此
从而BC=500×sin30°=250(m).
答:B处与河岸的距离BC为250m.
课堂练习
2.如图,某厂家新开发的一种电动车的大灯A射出的光线AB,AC与地面MN所形成的夹角∠ABN,∠ACN分别为
8°和15°,大灯A与地面的距离为1m,求该车大灯照亮地面的宽度BC(不考虑其他因素,结果精确到0.1m).
【选自教材P127 练习 第2题】
课堂练习
解:作AD⊥MN,垂足于D.
D
如图,在Rt△ABD中,∠ABD =8°,AD =1m,
因此
从而
同理CD≈3.73 m.
所以 BC=BD-CD≈3.4(m).
课堂练习
3.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m.这栋高楼有多高(结果精确到0.1m)?
解析:在Rt△ABD中,α=30°,AD=120.所以可以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
课堂练习
解:如图,α=30°,β=60°,AD=120m.
∵
∴BD=AD·tanα=120×tan30°=
CD=AD·tanβ=120×tan60°
∴BC=BD+CD
答:这栋高楼约高277.1m.
课堂练习
4.如图,在离树BC12米的A处,用测角仪测得树顶的仰角是30°,测角仪AD高为1.5米,求树高BC.(计算结果可保留根号)
分析:本题是一个直角梯形的问题,可以通过过点D作DE⊥BC于E,把求CB的问题转化求BE的长,从而可以在△BDE中利用三角函数.
课堂练习
解:过点D作DE⊥BC于E,则四边形DECA是矩形,
∴DE=AC=12 m.CE=AD=1.5 m.
在直角△BED中,∠BDE=30°,
∴BE=DE·tan30°=
∴BC=BE+EC=
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
水平线
铅垂线
视点
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第四章 锐角三角函数 4.4
解直角三角形的应用
湘教版(2024)九年级上册数学课件
4.4.1 与俯角、仰角有关的实际问题
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
新课导入
海中有一个小岛A,该岛四周10海里内有暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后,到达该岛的南偏西25°的C处,之后,货轮继续往东航行.
北
东
你认为货轮继续向东航行途中会有触礁的危险吗?
新课导入
北
东
D
分析:判断继续向东航行是否会有触礁危险,就是求AD的长度是否小于10海里.
在在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
探究新知
动脑筋
某探险者某天到达如图所示的点A处时,他准备估算出离他的目的地——海拔为3500m的山峰顶点B处的水平距离.你能帮他想出一个可行的办法吗?
新课讲解
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;从上往下看,视线与水平线的夹角叫做俯角.
铅垂线
水平线
视线
视线
仰角
俯角
视点
新课讲解
分析:如图,BD表示点B的海拔,AE表示点A的海拔,AC⊥BD,垂足为点C.先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.
新课讲解
如图,如果测得点A的海拔AE为1600m,仰角∠BAC=40°求A,B两点之间的水平距离AC(结果保留整数).
∵ BD = 3500m,AE = 1600m,AC⊥BD,∠BAC = 40°,
∴ 在Rt△ABC中,
∴
即AC≈2264(m).
因此,A,B两点之间的水平距离AC约为2264 m.
新课讲解
例1:如图, 在离上海东方明珠塔底部1000m的A处,用仪器测得塔顶的仰角∠BAC为25°,仪器距地面高AE为1.7m.求上海东方明珠塔的高度BD(结果精确到1m).
分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.
新课讲解
解:如图,在Rt△ABC中,∠BAC=25°,AC=1000 m,因此
从而BC=1000 × tan 25°≈ 466.3(m).
因此,上海东方明珠塔的高度
BD=466.3 + 1.7 = 468(m).
答:上海东方明珠塔的高度BD为468 m.
新课讲解
1.如图,一艘游船在离开码头A后,以和河岸成 30°角的方向行驶了500m到达B处,求B处与河岸的距离BC.
【选自教材P126 练习 第1题】
课堂练习
解:从点B作河岸线(看成直线段)的垂线,垂足为C,
在Rt△ABC中,∠C=90°,∠A=30°,AB=500m.
由于BC是∠A的对边,AB是斜边,因此
从而BC=500×sin30°=250(m).
答:B处与河岸的距离BC为250m.
课堂练习
2.如图,某厂家新开发的一种电动车的大灯A射出的光线AB,AC与地面MN所形成的夹角∠ABN,∠ACN分别为
8°和15°,大灯A与地面的距离为1m,求该车大灯照亮地面的宽度BC(不考虑其他因素,结果精确到0.1m).
【选自教材P127 练习 第2题】
课堂练习
解:作AD⊥MN,垂足于D.
D
如图,在Rt△ABD中,∠ABD =8°,AD =1m,
因此
从而
同理CD≈3.73 m.
所以 BC=BD-CD≈3.4(m).
课堂练习
3.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m.这栋高楼有多高(结果精确到0.1m)?
解析:在Rt△ABD中,α=30°,AD=120.所以可以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
课堂练习
解:如图,α=30°,β=60°,AD=120m.
∵
∴BD=AD·tanα=120×tan30°=
CD=AD·tanβ=120×tan60°
∴BC=BD+CD
答:这栋高楼约高277.1m.
课堂练习
4.如图,在离树BC12米的A处,用测角仪测得树顶的仰角是30°,测角仪AD高为1.5米,求树高BC.(计算结果可保留根号)
分析:本题是一个直角梯形的问题,可以通过过点D作DE⊥BC于E,把求CB的问题转化求BE的长,从而可以在△BDE中利用三角函数.
课堂练习
解:过点D作DE⊥BC于E,则四边形DECA是矩形,
∴DE=AC=12 m.CE=AD=1.5 m.
在直角△BED中,∠BDE=30°,
∴BE=DE·tan30°=
∴BC=BE+EC=
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
水平线
铅垂线
视点
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
