2025年广东省中考总复习·数学 第一部分 第一章 第1课时 实数 课件(共32张PPT)
文档属性
| 名称 | 2025年广东省中考总复习·数学 第一部分 第一章 第1课时 实数 课件(共32张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-18 21:49:39 | ||
图片预览









文档简介
(共32张PPT)
第一部分
同步练习
第1课时 实数
第一章 数与式
1.有理数.
(1)能用数轴上的点表示有理数,会比较有理数的大小.
(2)会求一个有理数的倒数、相反数、绝对值(绝对值符号内不
含字母).
(3)会用科学记数法表示数(包括在计算器上表示).
2.数的开方.
会用根号表示数的平方根、算术平方根、立方根.
3.理解乘方的意义,理解零指数幂、负整数指数幂的意义.
4.理解数轴的意义,能借助数轴理解相反数和绝对值的意义.
5.掌握有理数的有关运算,并能运用其解决简单的问题.
6.了解无理数和实数的概念.
7.能用有理数估计一个无理数的大致范围.
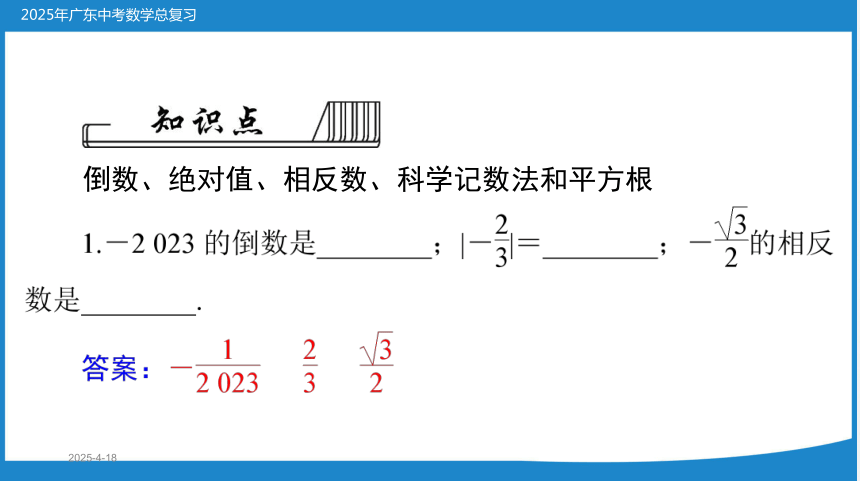
1.实数 a 的相反数是-a;若 a 与 b 互为相反数,则 a+b=
________.
0
1
m
1
相反数
负数
0
2.非零实数 m 的倒数是______;若 m 与 n 互为倒数,则 m·n
=________.
3.正数 a 的平方根表示为________,它们互为________,其中
叫作 a 的算术平方根;________ 没有平方根,0 的平方根是
______.
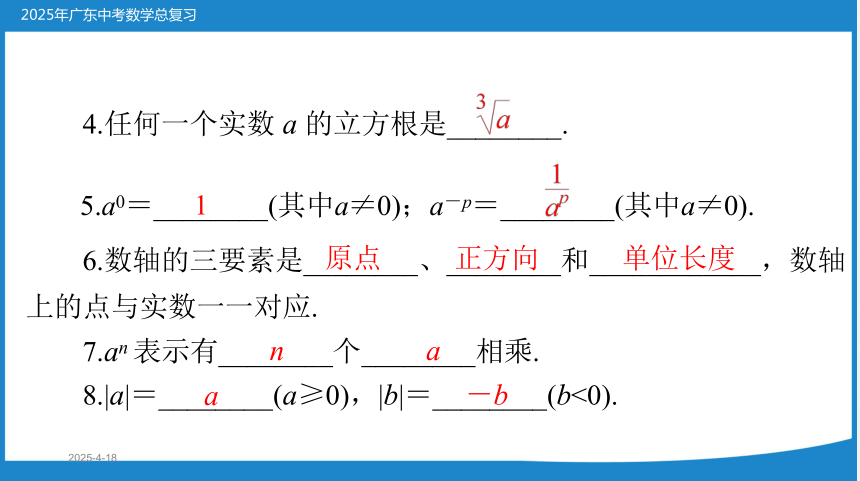
4.任何一个实数 a 的立方根是________.
1
6.数轴的三要素是________、________和____________,数轴
上的点与实数一一对应.
原点
正方向
单位长度
7.an 表示有________个________相乘.
8.|a|=________(a≥0),|b|=________(b<0).
5.a0=________(其中a≠0);a-p=________(其中a≠0).
n
a
a
-b
倒数、绝对值、相反数、科学记数法和平方根
2.(2022·广东)计算 22 的结果是(
)
A.1
C.2
B.
D.4
答案:D
3.(2024·广东)2024 年 6 月 6 日,嫦娥六号在距离地球约
384 000 千米外上演“太空牵手”,完成月球轨道的交会对接.
数据 384 000 用科学记数法表示为( )
A.3.84×104
B.3.84×105
C.3.84×106
D.38.4×105
答案:B
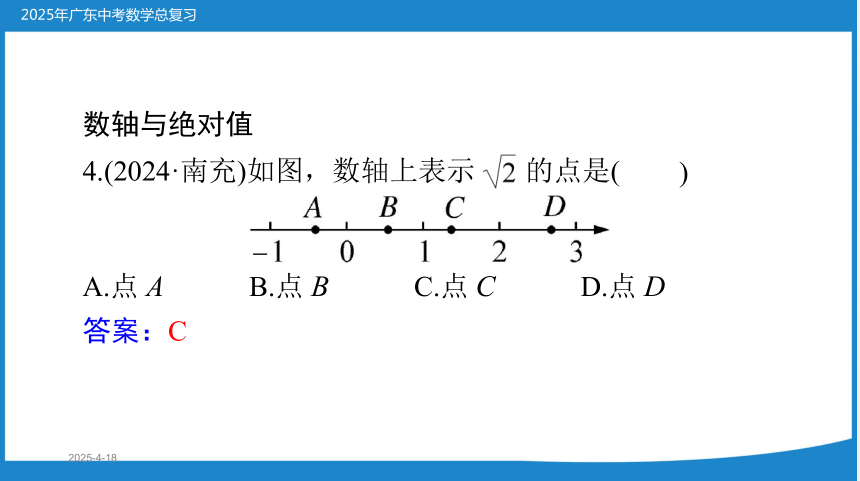
数轴与绝对值
4.(2024·南充)如图,数轴上表示 的点是(
)
A.点 A
B.点 B
C.点 C
D.点 D
答案:C
一个正数的平方根的特征
5.一个正数的平方根分别是 x+1 与 x-5,求 x 与这个正数的
值.
解:∵正数的平方根为 x+1 与 x-5,
∴x+1+x-5=0,即 x=2.
(x+1)2=(2+1)2=9.
∴x 的值是 2,这个正数的值是 9.
无理数
答案:A
答案:A
实数的运算及应用
答案:1
1.相反数:求一个数的相反数时,只需改变这个数的符号.
2.求一个数(或代数式)的绝对值时,必须先判断这个数是正
数、0 或负数,然后根据公式|a|=
计算.
3.用科学记数法表示一个数时,若这个数的绝对值大于 1,则
10 的指数为正整数; 若这个数的绝对值小于 1,则 10 的指数为
负整数.
1.(2023·深圳)如果+10 ℃表示零上 10 摄氏度,则零下 8 摄氏
度表示(
)
B.-8 ℃
D.-10 ℃
A.+8 ℃
C.+10 ℃
答案:B
)
B.2
2.(2022·广东)|-2|=(
A.-2
答案:B
3.(2024·烟台)实数 a,b,c 在数轴上的位置如图所示,下列
结论正确的是(
)
A.b+c>3
B.a-c<0
C.|a|>|c|
D.-2a<-2b
答案:B
4.(2023·长沙)下列各数中,是无理数的是(
)
A.
1
7
B.π
D.0
C.-1
答案:B
B.2 024 和
)
5.(2024·大庆)下列各组数中,互为相反数的是(
A.|-2 024|和-2 024
1
2 024
C.|-2 024|和 2 024
D.-2 024 和
1
2 024
答案:A
6.(2023·广东)2023 年 5 月 28 日,我国自主研发的 C919 国产
大飞机商业首航取得圆满成功.C919 可储存约 186 000 升燃油,将
)
B.1.86×105
D.186×103
数据 186 000 用科学记数法表示为(
A.0.186×105
C.18.6×104
答案:B
7.(2024·包头)若 m,n 互为倒数,且满足 m+mn=3,则 n
的值为(
)
A.
1
4
B.
1
2
C.2
D.4
答案:B
8.(2024·广州)四个数-10,-1,0,10 中,最小的数是(
)
A.-10
B.-1
C.0
D.10
答案:A
关系是(
)
B.a>c>b
D.b>c>a
A.b>a>c
C.a>b>c
答案:C
答案:>
答案:2
答案:220
12.(2024·广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为________.
解:原式=4-2+5=7
14.实数 a,b 在数轴上的对应点的位置如图所示,
解:原式=|a|-|b|-|a-b|
=-a-b+a-b=-2b.
16.(2024·河北)如图,有甲、乙两条数轴.甲数轴上的三点 A,
B,C 所对应的数依次为-4,2,32,乙数轴上的三点 D,E,F
所对应的数依次为 0,x,12.
(2)当点 A 与点 D 上下对齐时,点 B,C 恰好分别与点 E,F
上下对齐,求 x 的值.
解:(1)∵点 A,B,C 所对应的数依次为-4,2,32,
∴A,B,C 三点所对应的数的和为-4+2+32=30.
第一部分
同步练习
第1课时 实数
第一章 数与式
1.有理数.
(1)能用数轴上的点表示有理数,会比较有理数的大小.
(2)会求一个有理数的倒数、相反数、绝对值(绝对值符号内不
含字母).
(3)会用科学记数法表示数(包括在计算器上表示).
2.数的开方.
会用根号表示数的平方根、算术平方根、立方根.
3.理解乘方的意义,理解零指数幂、负整数指数幂的意义.
4.理解数轴的意义,能借助数轴理解相反数和绝对值的意义.
5.掌握有理数的有关运算,并能运用其解决简单的问题.
6.了解无理数和实数的概念.
7.能用有理数估计一个无理数的大致范围.
1.实数 a 的相反数是-a;若 a 与 b 互为相反数,则 a+b=
________.
0
1
m
1
相反数
负数
0
2.非零实数 m 的倒数是______;若 m 与 n 互为倒数,则 m·n
=________.
3.正数 a 的平方根表示为________,它们互为________,其中
叫作 a 的算术平方根;________ 没有平方根,0 的平方根是
______.
4.任何一个实数 a 的立方根是________.
1
6.数轴的三要素是________、________和____________,数轴
上的点与实数一一对应.
原点
正方向
单位长度
7.an 表示有________个________相乘.
8.|a|=________(a≥0),|b|=________(b<0).
5.a0=________(其中a≠0);a-p=________(其中a≠0).
n
a
a
-b
倒数、绝对值、相反数、科学记数法和平方根
2.(2022·广东)计算 22 的结果是(
)
A.1
C.2
B.
D.4
答案:D
3.(2024·广东)2024 年 6 月 6 日,嫦娥六号在距离地球约
384 000 千米外上演“太空牵手”,完成月球轨道的交会对接.
数据 384 000 用科学记数法表示为( )
A.3.84×104
B.3.84×105
C.3.84×106
D.38.4×105
答案:B
数轴与绝对值
4.(2024·南充)如图,数轴上表示 的点是(
)
A.点 A
B.点 B
C.点 C
D.点 D
答案:C
一个正数的平方根的特征
5.一个正数的平方根分别是 x+1 与 x-5,求 x 与这个正数的
值.
解:∵正数的平方根为 x+1 与 x-5,
∴x+1+x-5=0,即 x=2.
(x+1)2=(2+1)2=9.
∴x 的值是 2,这个正数的值是 9.
无理数
答案:A
答案:A
实数的运算及应用
答案:1
1.相反数:求一个数的相反数时,只需改变这个数的符号.
2.求一个数(或代数式)的绝对值时,必须先判断这个数是正
数、0 或负数,然后根据公式|a|=
计算.
3.用科学记数法表示一个数时,若这个数的绝对值大于 1,则
10 的指数为正整数; 若这个数的绝对值小于 1,则 10 的指数为
负整数.
1.(2023·深圳)如果+10 ℃表示零上 10 摄氏度,则零下 8 摄氏
度表示(
)
B.-8 ℃
D.-10 ℃
A.+8 ℃
C.+10 ℃
答案:B
)
B.2
2.(2022·广东)|-2|=(
A.-2
答案:B
3.(2024·烟台)实数 a,b,c 在数轴上的位置如图所示,下列
结论正确的是(
)
A.b+c>3
B.a-c<0
C.|a|>|c|
D.-2a<-2b
答案:B
4.(2023·长沙)下列各数中,是无理数的是(
)
A.
1
7
B.π
D.0
C.-1
答案:B
B.2 024 和
)
5.(2024·大庆)下列各组数中,互为相反数的是(
A.|-2 024|和-2 024
1
2 024
C.|-2 024|和 2 024
D.-2 024 和
1
2 024
答案:A
6.(2023·广东)2023 年 5 月 28 日,我国自主研发的 C919 国产
大飞机商业首航取得圆满成功.C919 可储存约 186 000 升燃油,将
)
B.1.86×105
D.186×103
数据 186 000 用科学记数法表示为(
A.0.186×105
C.18.6×104
答案:B
7.(2024·包头)若 m,n 互为倒数,且满足 m+mn=3,则 n
的值为(
)
A.
1
4
B.
1
2
C.2
D.4
答案:B
8.(2024·广州)四个数-10,-1,0,10 中,最小的数是(
)
A.-10
B.-1
C.0
D.10
答案:A
关系是(
)
B.a>c>b
D.b>c>a
A.b>a>c
C.a>b>c
答案:C
答案:>
答案:2
答案:220
12.(2024·广州)如图,把R1,R2,R3三个电阻串联起来,线路AB上的电流为I,电压为U,则U=IR1+IR2+IR3,当R1=20.3,R2=31.9,R3=47.8,I=2.2时,U的值为________.
解:原式=4-2+5=7
14.实数 a,b 在数轴上的对应点的位置如图所示,
解:原式=|a|-|b|-|a-b|
=-a-b+a-b=-2b.
16.(2024·河北)如图,有甲、乙两条数轴.甲数轴上的三点 A,
B,C 所对应的数依次为-4,2,32,乙数轴上的三点 D,E,F
所对应的数依次为 0,x,12.
(2)当点 A 与点 D 上下对齐时,点 B,C 恰好分别与点 E,F
上下对齐,求 x 的值.
解:(1)∵点 A,B,C 所对应的数依次为-4,2,32,
∴A,B,C 三点所对应的数的和为-4+2+32=30.
同课章节目录
