2025年广东省中考总复习·数学 第一部分 第三章 第15课时 二次函数(2) 课件(共39张PPT)
文档属性
| 名称 | 2025年广东省中考总复习·数学 第一部分 第三章 第15课时 二次函数(2) 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-19 07:04:04 | ||
图片预览










文档简介
(共39张PPT)
第15课时 二次函数(2)
第三章 函数
1.掌握用待定系数法确定二次函数的解析式.
2.掌握二次函数图象的平移.
3.会利用二次函数的图象求一元二次方程的近似解.会求二次
函数图象与坐标轴的交点坐标.
4.能用二次函数解决实际问题.
1.用待定系数法求二次函数的解析式:
(1)一般式:________________.已知图象上三点或三对 x,y
的值,通常选择一般式.
y=ax2+bx+c
y=a(x-h)2+k
(2)顶点式:__________________.已知图象的顶点或对称轴,
通常选择顶点式.
y=a(x-x1)(x-x2)
(3)交点式:___________________.已知图象与 x 轴的交点坐
标 x1,x2,通常选择交点式.
2.二次函数图象的平移:
y=ax2±k
y=a(x±h)2
抛物线的平移主要是移动顶点的位置,将 y=ax2 的图象沿
着y 轴(上“+”,下“-”)平移 k(k>0)个单位长度得到函数
_____________,将 y=ax2 的图象沿着 x 轴(左“+”,右“-”)
平移 h(h>0)个单位长度得到_______________.在平移之前先将函
数解析式化为顶点式,再来平移.
3.二次函数图象与坐标轴的公共点:
(1)y 轴与抛物线 y=ax2+bx+c 的交点为________.
(2)二次函数 y=ax2+bx+c 的图象与 x 轴的两个公共点的横坐
标 x1,x2,是对应一元二次方程 ax2+bx+c=0 的两个实数根.抛物
线与 x 轴的公共点情况可以由对应的一元二次方程的根的判别式
判定:
(0, c)
两个
相切
相离
①有________公共点 Δ>0 抛物线与 x 轴相交.
②有一个公共点(顶点在 x 轴上) Δ=0 抛物线与 x 轴_____.
③没有公共点 Δ<0 抛物线与 x 轴________.
二次函数图象的平移
1.将抛物线 y=2x2 向下平移 2 个单位长度,所得的抛物线
的解析式为__________________.
答案:y=2x2-2
二次函数图象与坐标轴的交点
2.抛物线 y=2x2+3x-4 与 y 轴的交点坐标是___________.
答案:(0,-4)
二次函数图象与一元二次方程的解
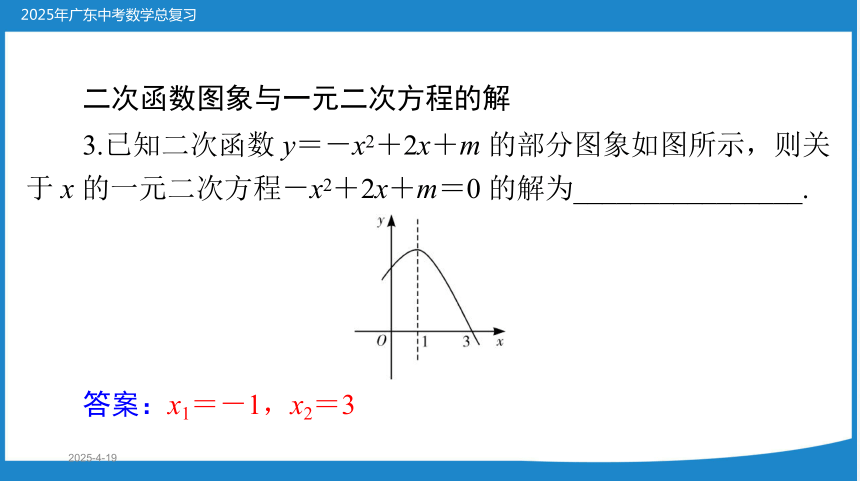
3.已知二次函数 y=-x2+2x+m 的部分图象如图所示,则关
于 x 的一元二次方程-x2+2x+m=0 的解为________________.
答案:x1=-1,x2=3
用待定系数法确定二次函数解析式
4.已知二次函数的图象经过点(0,1),(2,1)和(3,4),求该
二次函数的解析式.
1.图象平移的本质
(1)抛物线的上下平移本质上是 y 的增减变化,因此对于无论
何种二次函数表达形式,只需结合口诀“上加下减”在函数表达
式的最后进行加减即可.如 y=-3(x+1)(x-2)向上平移 3 个单位长
度得到 y=-3(x+1)(x-2)+3;如 y=2(x-1)2+1 向下平移 2 个单
位长度得到 y=2(x-1)2+1-2.
(2)抛物线的左右平移本质上是 x 的增减变化,因此对于无论
何种二次函数表达形式,只需结合口诀“左加右减”对 x 作等量
代换即可.如 y=-x2+2x+1 向右平移 3 个单位长度得到 y=-(x
-3)2+2(x-3)+1;如 y=3(x+1)(x-2)向左平移 2 个单位长度得
到 y=3[(x+2)+1][(x+2)-2].
2.求抛物线与 x 轴和 y 轴的交点坐标容易把横、纵坐标写反,
需特别注意.
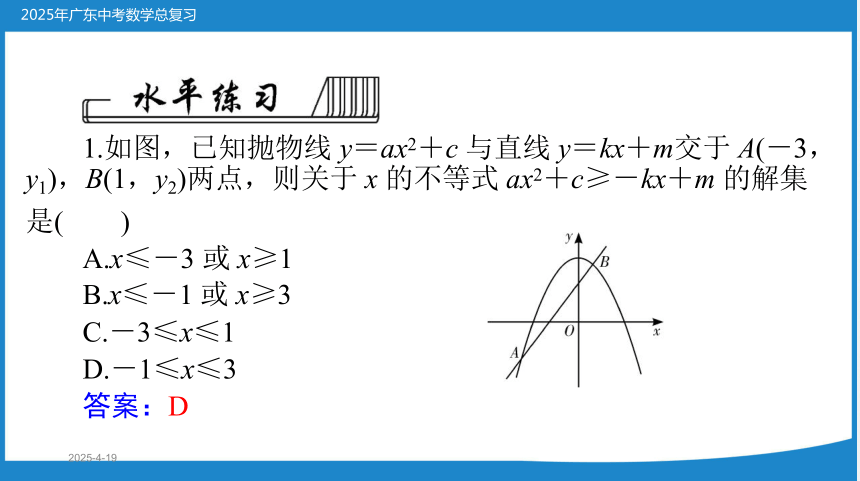
1.如图,已知抛物线 y=ax2+c 与直线 y=kx+m交于 A(-3,
y1),B(1,y2)两点,则关于 x 的不等式 ax2+c≥-kx+m 的解集
是( )
A.x≤-3 或 x≥1
B.x≤-1 或 x≥3
C.-3≤x≤1
D.-1≤x≤3
答案:D
2.(2022·绍兴)已知抛物线 y=x2+mx 的对称轴为直线 x=2,则
)
关于 x 的方程 x2+mx=5 的根是(
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=-5
D.x1=-1,x2=5
答案:D
3.(2023·徐州)在平面直角坐标系中,将二次函数 y=(x+1)2+
3 的图象向右平移 2 个单位长度,再向下平移 1 个单位长度,所得
)
B.y=(x-1)2+2
D.y=(x+3)2+4
抛物线对应的函数表达式为(
A.y=(x+3)2+2
C.y=(x-1)2+4
答案:B
4.(2023·达州)如图,抛物线 y=ax2+bx+c(a,b,c 为常数)
关于直线 x=1 对称.有下列五个结论:①abc>0;②2a+b=0;
③4a+2b +c >0 ;④am2 +bm>a +b ;⑤3a +c >0.其中正
确的有( )
A.4 个
B.3 个
C.2 个
D.1 个
答案:B
5. 抛物线 y=x2 -4x +c 的顶点在 x 轴上,则 c 的值是
(
)
A.0
B.4
C.-4
D.2
答案:B
答案:D
A.x<-1
B.-1<x<0
C.0<x<2
D.x>1
答案:D
x … -1 0 1 2 3 …
y … 3 0 -1 m 3 …
8.已知抛物线 y=ax2+bx+c 上的部分点的横坐标x 与纵坐标
y 的对应值如表:
以下结论正确的是(
)
A.抛物线 y=ax2+bx+c 的开口向下
B.当 x<3 时,y 随 x 增大而增大
C.方程 ax2+bx+c=0 的根为 0 和 2
D.当 y>0 时,x 的取值范围是 0答案:C
9.(2024·滨州)将抛物线 y=-x2 先向右平移 1 个单位长度,
再向上平移 2 个单位长度,则平移后抛物线的顶点坐标为_____.
答案:(1,2)
10.(2022·黔东南州)在平面直角坐标系中,将抛物线 y=x2+2x
-1 先绕原点旋转 180°,再向下平移 5 个单位长度,所得到的抛
物线的顶点坐标是________.
答案:(1,-3)
11.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图
所示,在抛物线各个位置上,水珠的竖直高度 y(单位:m)与它距
离喷头的水平距离 x(单位:m)之间满足函数关系式 y=-2x2+4x
+1,则喷出水珠的最大高度是________m.
答案:3
12.(2024·宁夏)若二次函数 y=2x2-x+m 的图象与 x 轴有交
点,则 m 的取值范围是________.
13.(2024·福建)如图,已知二次函数 y=x2+bx+c 的图象与 x
轴交于 A,B 两点,与 y 轴交于点 C,其中 A(-2,0),C(0,-2).
(1)求二次函数的解析式.
(2)若 P 是二次函数图象上的一点,且点 P 在第二象限,线段
PC 交 x 轴于点 D,△PDB 的面积是△CDB 的面积的 2 倍,求点P
的坐标.
解:(1)由题意,将 A(-2,0),C(0,-2)代入 y=x2+bx+c,
∴二次函数的解析式为 y=x2+x-2.
(2)由题意,设 P(m,n)(m<0,n>0),
又△PDB 的面积是△CDB 的面积的 2 倍,
又 CO=2,∴n=2CO=4.由 m2+m-2=4,
∴m1=-3,m2=2 (舍去).∴点 P 的坐标为 (-3,4).
14.(2024·广东)广东省全力实施“百县千镇万村高质量发展
工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远
销欧美.某果商以每吨 2万元的价格收购早熟荔枝,销往国外,若
按每吨 5 万元出售,平均每天可售出 100 吨.市场调查反映:如果
每吨降价 1 万元,每天销售量相应增加 50 吨.该果商如何定价才
能使每天的“利润”或“销售收入”最大?请求出其最大值.(题
中“元”为人民币)
解:设该果商定价 x 万元时,每天的“利润”为 w 万元,
每天的“销售收入”为 y 万元,由题意,得
w=(x-2)[100+50(5-x)]
=-50(x-4.5)2+312.5,
∵-50<0,
∴w 随 x 的增大而减小,
∴当 x=4.5 时,w 有最大值,最大值为 312.5 万元.
y=x[100+50(5-x)]=-50(x-3.5)2+612.5,
∵-50<0,
∴y 随 x 的增大而减小,
∴当 x=3.5 时,y 有最大值,最大值为 612.5 万元.
答:该果商定价为 4.5 万元时才能使每天的“利润”最大,
其最大值为 312.5 万元,定价为 3.5 万元时才能使每天的“销售
收入”最大,其最大值为 612.5 万元.
(3)如图 2,点 P 在第二象限,x2=-2x1,若点 M 在直线 PQ
上,且横坐标为 x1-1,过点 M 作 MN⊥x 轴于点 N,求线段 MN
长度的最大值.
图 1
图 2
(1)解:将点 A 的坐标代入 y=-x2+c,
得 5=-4+c,则 c=9,
∴二次函数的解析式为 y=-x2+9.
(2)证明:在y=-x2+9中,令y=0,则x=±3,
则点 B(3,0).
由点 A,B 的坐标得直线 AB 的解析式为 y=-x+3.
16.(2022·广东)如图,抛物线 y=x2+bx+c(b,c 是常数)的顶
点为 C,与 x 轴交于 A,B 两点,A(1,0),AB=4,点 P 为线段
AB 上的动点,过 P 作 PQ∥BC 交 AC 于点 Q.
(1)求该抛物线的解析式.
(2)求△CPQ 面积的最大值,并求此时 P 点坐标.
解:(1)∵A(1,0),AB=4,
∴B(-3,0).
(2)如图,过Q作QE⊥x轴于点E,过点C作CF⊥x 轴于点F,
设 P(m,0),则 PA =1-m.
∵y=x2+2x-3=(x+1)2-4,
∴C(-1,-4),CF=4.
第15课时 二次函数(2)
第三章 函数
1.掌握用待定系数法确定二次函数的解析式.
2.掌握二次函数图象的平移.
3.会利用二次函数的图象求一元二次方程的近似解.会求二次
函数图象与坐标轴的交点坐标.
4.能用二次函数解决实际问题.
1.用待定系数法求二次函数的解析式:
(1)一般式:________________.已知图象上三点或三对 x,y
的值,通常选择一般式.
y=ax2+bx+c
y=a(x-h)2+k
(2)顶点式:__________________.已知图象的顶点或对称轴,
通常选择顶点式.
y=a(x-x1)(x-x2)
(3)交点式:___________________.已知图象与 x 轴的交点坐
标 x1,x2,通常选择交点式.
2.二次函数图象的平移:
y=ax2±k
y=a(x±h)2
抛物线的平移主要是移动顶点的位置,将 y=ax2 的图象沿
着y 轴(上“+”,下“-”)平移 k(k>0)个单位长度得到函数
_____________,将 y=ax2 的图象沿着 x 轴(左“+”,右“-”)
平移 h(h>0)个单位长度得到_______________.在平移之前先将函
数解析式化为顶点式,再来平移.
3.二次函数图象与坐标轴的公共点:
(1)y 轴与抛物线 y=ax2+bx+c 的交点为________.
(2)二次函数 y=ax2+bx+c 的图象与 x 轴的两个公共点的横坐
标 x1,x2,是对应一元二次方程 ax2+bx+c=0 的两个实数根.抛物
线与 x 轴的公共点情况可以由对应的一元二次方程的根的判别式
判定:
(0, c)
两个
相切
相离
①有________公共点 Δ>0 抛物线与 x 轴相交.
②有一个公共点(顶点在 x 轴上) Δ=0 抛物线与 x 轴_____.
③没有公共点 Δ<0 抛物线与 x 轴________.
二次函数图象的平移
1.将抛物线 y=2x2 向下平移 2 个单位长度,所得的抛物线
的解析式为__________________.
答案:y=2x2-2
二次函数图象与坐标轴的交点
2.抛物线 y=2x2+3x-4 与 y 轴的交点坐标是___________.
答案:(0,-4)
二次函数图象与一元二次方程的解
3.已知二次函数 y=-x2+2x+m 的部分图象如图所示,则关
于 x 的一元二次方程-x2+2x+m=0 的解为________________.
答案:x1=-1,x2=3
用待定系数法确定二次函数解析式
4.已知二次函数的图象经过点(0,1),(2,1)和(3,4),求该
二次函数的解析式.
1.图象平移的本质
(1)抛物线的上下平移本质上是 y 的增减变化,因此对于无论
何种二次函数表达形式,只需结合口诀“上加下减”在函数表达
式的最后进行加减即可.如 y=-3(x+1)(x-2)向上平移 3 个单位长
度得到 y=-3(x+1)(x-2)+3;如 y=2(x-1)2+1 向下平移 2 个单
位长度得到 y=2(x-1)2+1-2.
(2)抛物线的左右平移本质上是 x 的增减变化,因此对于无论
何种二次函数表达形式,只需结合口诀“左加右减”对 x 作等量
代换即可.如 y=-x2+2x+1 向右平移 3 个单位长度得到 y=-(x
-3)2+2(x-3)+1;如 y=3(x+1)(x-2)向左平移 2 个单位长度得
到 y=3[(x+2)+1][(x+2)-2].
2.求抛物线与 x 轴和 y 轴的交点坐标容易把横、纵坐标写反,
需特别注意.
1.如图,已知抛物线 y=ax2+c 与直线 y=kx+m交于 A(-3,
y1),B(1,y2)两点,则关于 x 的不等式 ax2+c≥-kx+m 的解集
是( )
A.x≤-3 或 x≥1
B.x≤-1 或 x≥3
C.-3≤x≤1
D.-1≤x≤3
答案:D
2.(2022·绍兴)已知抛物线 y=x2+mx 的对称轴为直线 x=2,则
)
关于 x 的方程 x2+mx=5 的根是(
A.x1=0,x2=4
B.x1=1,x2=5
C.x1=1,x2=-5
D.x1=-1,x2=5
答案:D
3.(2023·徐州)在平面直角坐标系中,将二次函数 y=(x+1)2+
3 的图象向右平移 2 个单位长度,再向下平移 1 个单位长度,所得
)
B.y=(x-1)2+2
D.y=(x+3)2+4
抛物线对应的函数表达式为(
A.y=(x+3)2+2
C.y=(x-1)2+4
答案:B
4.(2023·达州)如图,抛物线 y=ax2+bx+c(a,b,c 为常数)
关于直线 x=1 对称.有下列五个结论:①abc>0;②2a+b=0;
③4a+2b +c >0 ;④am2 +bm>a +b ;⑤3a +c >0.其中正
确的有( )
A.4 个
B.3 个
C.2 个
D.1 个
答案:B
5. 抛物线 y=x2 -4x +c 的顶点在 x 轴上,则 c 的值是
(
)
A.0
B.4
C.-4
D.2
答案:B
答案:D
A.x<-1
B.-1<x<0
C.0<x<2
D.x>1
答案:D
x … -1 0 1 2 3 …
y … 3 0 -1 m 3 …
8.已知抛物线 y=ax2+bx+c 上的部分点的横坐标x 与纵坐标
y 的对应值如表:
以下结论正确的是(
)
A.抛物线 y=ax2+bx+c 的开口向下
B.当 x<3 时,y 随 x 增大而增大
C.方程 ax2+bx+c=0 的根为 0 和 2
D.当 y>0 时,x 的取值范围是 0
9.(2024·滨州)将抛物线 y=-x2 先向右平移 1 个单位长度,
再向上平移 2 个单位长度,则平移后抛物线的顶点坐标为_____.
答案:(1,2)
10.(2022·黔东南州)在平面直角坐标系中,将抛物线 y=x2+2x
-1 先绕原点旋转 180°,再向下平移 5 个单位长度,所得到的抛
物线的顶点坐标是________.
答案:(1,-3)
11.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图
所示,在抛物线各个位置上,水珠的竖直高度 y(单位:m)与它距
离喷头的水平距离 x(单位:m)之间满足函数关系式 y=-2x2+4x
+1,则喷出水珠的最大高度是________m.
答案:3
12.(2024·宁夏)若二次函数 y=2x2-x+m 的图象与 x 轴有交
点,则 m 的取值范围是________.
13.(2024·福建)如图,已知二次函数 y=x2+bx+c 的图象与 x
轴交于 A,B 两点,与 y 轴交于点 C,其中 A(-2,0),C(0,-2).
(1)求二次函数的解析式.
(2)若 P 是二次函数图象上的一点,且点 P 在第二象限,线段
PC 交 x 轴于点 D,△PDB 的面积是△CDB 的面积的 2 倍,求点P
的坐标.
解:(1)由题意,将 A(-2,0),C(0,-2)代入 y=x2+bx+c,
∴二次函数的解析式为 y=x2+x-2.
(2)由题意,设 P(m,n)(m<0,n>0),
又△PDB 的面积是△CDB 的面积的 2 倍,
又 CO=2,∴n=2CO=4.由 m2+m-2=4,
∴m1=-3,m2=2 (舍去).∴点 P 的坐标为 (-3,4).
14.(2024·广东)广东省全力实施“百县千镇万村高质量发展
工程”,2023年农产品进出口总额居全国首位,其中荔枝鲜果远
销欧美.某果商以每吨 2万元的价格收购早熟荔枝,销往国外,若
按每吨 5 万元出售,平均每天可售出 100 吨.市场调查反映:如果
每吨降价 1 万元,每天销售量相应增加 50 吨.该果商如何定价才
能使每天的“利润”或“销售收入”最大?请求出其最大值.(题
中“元”为人民币)
解:设该果商定价 x 万元时,每天的“利润”为 w 万元,
每天的“销售收入”为 y 万元,由题意,得
w=(x-2)[100+50(5-x)]
=-50(x-4.5)2+312.5,
∵-50<0,
∴w 随 x 的增大而减小,
∴当 x=4.5 时,w 有最大值,最大值为 312.5 万元.
y=x[100+50(5-x)]=-50(x-3.5)2+612.5,
∵-50<0,
∴y 随 x 的增大而减小,
∴当 x=3.5 时,y 有最大值,最大值为 612.5 万元.
答:该果商定价为 4.5 万元时才能使每天的“利润”最大,
其最大值为 312.5 万元,定价为 3.5 万元时才能使每天的“销售
收入”最大,其最大值为 612.5 万元.
(3)如图 2,点 P 在第二象限,x2=-2x1,若点 M 在直线 PQ
上,且横坐标为 x1-1,过点 M 作 MN⊥x 轴于点 N,求线段 MN
长度的最大值.
图 1
图 2
(1)解:将点 A 的坐标代入 y=-x2+c,
得 5=-4+c,则 c=9,
∴二次函数的解析式为 y=-x2+9.
(2)证明:在y=-x2+9中,令y=0,则x=±3,
则点 B(3,0).
由点 A,B 的坐标得直线 AB 的解析式为 y=-x+3.
16.(2022·广东)如图,抛物线 y=x2+bx+c(b,c 是常数)的顶
点为 C,与 x 轴交于 A,B 两点,A(1,0),AB=4,点 P 为线段
AB 上的动点,过 P 作 PQ∥BC 交 AC 于点 Q.
(1)求该抛物线的解析式.
(2)求△CPQ 面积的最大值,并求此时 P 点坐标.
解:(1)∵A(1,0),AB=4,
∴B(-3,0).
(2)如图,过Q作QE⊥x轴于点E,过点C作CF⊥x 轴于点F,
设 P(m,0),则 PA =1-m.
∵y=x2+2x-3=(x+1)2-4,
∴C(-1,-4),CF=4.
同课章节目录
